17 May 2014

概要

numpy の pseudo inverse は昔読んだ generalized inverse とは少し異なっている。Rank の小さい行列、またゼロ行列さえも pseudo inverse が存在する。それらについての PythonSf 数値実験と検討を報告する。

擬似逆行列の定義と具体例

ここに wikipedia に擬似逆行列の定義と解説が書かれてます。下に定義を再掲します。

擬似逆行列の定義

任意の行列 A に対し、その Hermite 行列 A.d とするとき、以下の条件を満足する擬似逆行列 Apsd は常に存在し、また唯一つ定まる：

条件 1: Apsd は広義可逆元である：
    A Apsd A == A,
    Apsd A Apsd == Apsd.

条件 2: A Apsd および Apsd A はエルミート行列である：
    (A Apsd).d == A Apsd,
    (Apsd A).d == Apsd A.

大部分の方は上の定義を見せられても半分狐に摘まれたような気分でしょう。広義可逆元なんて言葉は初めて見る方が殆どでしょう。こういう時は具体例での数値実験で式の意味を明確にしましょう。幸い np.linalg.pinv(..) 関数が擬似逆行列を生成して返してくれます。なお np.linalg.pinv(..) 関数は np.ufunc ではないのですが、ClTensor インスタンスを引数に与えると ClTensor インスタンスの擬似逆行列を返してくれます。実質的に np.ufunc です。

2x3 ランダム複素行列:A とその擬似逆行列:Apsd

seed(0); A=randn(3,2)+ `i randn(3,2); A
===============================
[[ 1.76405235+0.95008842j  0.40015721-0.15135721j]
 [ 0.97873798-0.10321885j  2.24089320+0.4105985j ]
 [ 1.86755799+0.14404357j -0.97727788+1.45427351j]]
---- ClTensor ----

seed(0); A=randn(3,2)+ `i randn(3,2); Apsd=np.linalg.pinv(A); Apsd
===============================
[[ 0.23850346-0.14941741j  0.07430511-0.08088406j  0.20359156+0.05059478j]
 [ 0.06670345+0.11764575j  0.28298303-0.01310121j -0.15924128-0.11027123j]]
---- ClTensor ----

seed(0); A=randn(3,2)+ `i randn(3,2); Apsd=np.linalg.pinv(A); Apsd A
===============================
[[  1.00000000e+00 -4.16333634e-17j  -2.49800181e-16 +0.00000000e+00j]
 [  1.11022302e-16 +0.00000000e+00j   1.00000000e+00 -6.93889390e-17j]]
---- ClTensor ----

# 上の三つの式の PythonSf Open 判コード
seed(0); A=randn(3,2)+ `i*randn(3,2); A
===============================
[[ 1.76405235+0.95008842j  0.40015721-0.15135721j]
 [ 0.97873798-0.10321885j  2.24089320+0.4105985j ]
 [ 1.86755799+0.14404357j -0.97727788+1.45427351j]]
---- ClTensor ----

seed(0); A=randn(3,2)+ `i*randn(3,2); Apsd=np.linalg.pinv(A); Apsd
===============================
[[ 0.23850346-0.14941741j  0.07430511-0.08088406j  0.20359156+0.05059478j]
 [ 0.06670345+0.11764575j  0.28298303-0.01310121j -0.15924128-0.11027123j]]
---- ClTensor ----

seed(0); A=randn(3,2)+ `i*randn(3,2); Apsd=np.linalg.pinv(A); Apsd A
===============================
[[  1.00000000e+00 -4.16333634e-17j  -2.49800181e-16 +0.00000000e+00j]
 [  1.11022302e-16 +0.00000000e+00j   1.00000000e+00 -6.93889390e-17j]]
---- ClTensor ----

3x2 行列の擬似逆行列は 2x3 行列です。Apsd A と A Apsd どちらの積演算も可能です。Apsd は右擬似逆行列であると同時に左擬似逆行列にもなっています。

Apsd A が「単位行列 [[1,0],[0,1]] になっていない」と言わないでください。実数のコンピュータ計算には誤差がつき物です。行列の prety print 関数 pp(..) を使えば、少し上の結果が見やすくなります。ただし六桁以下の小さな値は表示されません。また現在のところ pp(..) 関数は PythonSfOpen には移植できていません。

pp(..) による Apsd A と A Apsc

seed(0); A=randn(3,2)+ `i randn(3,2); Apsd=np.linalg.pinv(A); pp(Apsd A);
[[ 1, 0]
,[ 0, 1]]
-------- pp --

seed(0); A=randn(3,2)+ `i randn(3,2); Apsd=np.linalg.pinv(A); pp(A Apsd);
[[           0.607191,  0.31918-0.120161j, 0.230665+0.262658j]
,[  0.31918+0.120161j,           0.703891, -0.10708-0.283986j]
,[ 0.230665-0.262658j, -0.10708+0.283986j,           0.688919]]
-------- pp --

上の計算で A Apsd が Hermite になっていることに注意を向けておいてください。A Apsd を単位行列にできなくなった代償として特殊な Hermite 行列になります。

定義「条件 1」の確認

先の擬似逆行列の定義における「条件 1」が成り立つことを数値実験で確認してみましょう。

定義「条件 1」の確認

seed(0); A=randn(3,2)+ `i randn(3,2); Apsd=np.linalg.pinv(A); (A Apsd A) ~== A
===============================
True

seed(0); A=randn(3,2)+ `i randn(3,2); Apsd=np.linalg.pinv(A); (Apsd A Apsd) ~== Apsd
===============================
True

# 上の二つの PythonSf Open 判コード
seed(0); A=randn(3,2)+ `i*randn(3,2); Apsd=np.linalg.pinv(A); np.allclose(np.dot(A, np.dot(Apsd,A)), A)
===============================
True
seed(0); A=randn(3,2)+ `i*randn(3,2); Apsd=np.linalg.pinv(A); np.allclose(np.dot(Apsd, np.dot(A, Apsd)), Apsd)
===============================
True

~== は PythonSf でのユーザー演算子拡張であり、customize.py の中で nearlyEq(..) 関数に割り振っています。現在のところプリプロセッサがユーザー演算子の優先順位を一律に高くしているので、丸括弧での優先順位指定が必須です。無駄に丸括弧が必要なデメリットはありますが、可読性を向上してくれます。

PythonSf Open 判でも「条件 1」の確認計算は可能です。でも積演算子 * および np.dot(..) を追加し、 ~== ユーザー演算子のかわりに np.allclose(..) わねばなりません。この結果 PythonSf Open 判のコードは Python のコードと同じになってしまいました。でも可読性は悪化しています。

A Apsd または Apsd A が単位行列であれば (A Apsd A) ~== A と (Apsd A Apsd) ~== Apsd が成り立ちます。だからこの二つの条件は擬似逆行列であるための必要条件とみなして良さそうです。

ちなみに擬似逆行列は行列式が 0 の逆行列が存在しない正方行列についても存在します。そのときにも (A Apsd A) ~== A と (Apsd A Apsd) ~== Apsd が成り立ちます。もちろん Apsd A, A Apsd は単位行列になりません。

行列式が 0 のときの定義「条件 1」の確認

A =~[np.arange(3*3)].reshape(3,3); A
===============================
[[ 0.  1.  2.]
 [ 3.  4.  5.]
 [ 6.  7.  8.]]
---- ClTensor ----

# 行列式が 0
A=~[np.arange(3*3).reshape(3,3)]; A.m_dtrm
===============================
0.0

# 擬似逆行列 Apsd
A=~[np.arange(3*3).reshape(3,3)]; A.m_dtrm ; Apsd=np.linalg.pinv(A); pp(Apsd)
[[  -0.555556, -0.166667,  0.222222]
,[ -0.0555556,         0, 0.0555556]
,[   0.444444,  0.166667, -0.111111]]
-------- pp --
===============================
None

# Apsd A は単位行列にならない
A=~[np.arange(3*3).reshape(3,3)]; A.m_dtrm ; Apsd=np.linalg.pinv(A); Apsd A
===============================
[[ 0.83333333  0.33333333 -0.16666667]
 [ 0.33333333  0.33333333  0.33333333]
 [-0.16666667  0.33333333  0.83333333]]
---- ClTensor ----

A=~[np.arange(3*3).reshape(3,3)]; A.m_dtrm ; Apsd=np.linalg.pinv(A); (A Apsd) ~== (Apsd A)
===============================
True

# でも  (A Apsd A) ~== A は成り立つ
A=~[np.arange(3*3).reshape(3,3)]; A.m_dtrm ; Apsd=np.linalg.pinv(A); (A Apsd A) ~== A
===============================
True

# でも  (Apsd A Apsd) ~== Apsd も成り立つ
A=~[np.arange(3*3).reshape(3,3)]; A.m_dtrm ; Apsd=np.linalg.pinv(A); (Apsd A Apsd) ~== Apsd
===============================
True

定義「条件2」の確認

先の擬似行列の定義における「条件 2」が成り立つことも数値実験で確認してみましょう。

定義「条件 2」の確認

seed(0); A=randn(2,3)+ `i randn(2,3); Apsd=np.linalg.pinv(A); (A Apsd).d ~== (A Apsd)
===============================
True

seed(0); A=randn(2,3)+ `i randn(2,3); Apsd=np.linalg.pinv(A); (Apsd A).d ~== (Apsd A)
===============================
True

# 上の二つの式の PythonSf Open 判コード
seed(0); A=randn(2,3)+ `i*randn(2,3); Apsd=np.linalg.pinv(A); np.allclose(np.dot(A, Apsd).conj().T, np.dot(A, Apsd))
===============================
True

seed(0); A=randn(2,3)+ `i*randn(2,3); Apsd=np.linalg.pinv(A); np.allclose(np.dot(Apsd, A).conj().T, np.dot(Apsd, A))
===============================
True

しかしこの二条件を示されるだけでは、擬似逆行列について理解した気になれません。先の wikipedia には具体例でも論じているのですが、それでも私には理解した気になれません。もう少し色々と突っついてみましょう。

(A.d A)^-1 A.d による擬似逆行列

A が (m,n) 行列で m<n, rank(A)==m のとき、その擬似逆行列は (A.d A)^-1 A.d で表されます。

擬似逆行列が (A.d A)^-1 A.d となることの数値確認

# rank 2 の 3x2 行列のとき、pseudo inverse は (A.d A)^-1 A.d で作れる
seed(0); A=randn(3,2)+ `i randn(3,2); (A.d A)^-1 A.d
===============================
[[ 0.23850346-0.14941741j  0.07430511-0.08088406j  0.20359156+0.05059478j]
 [ 0.06670345+0.11764575j  0.28298303-0.01310121j -0.15924128-0.11027123j]]
---- ClTensor ----

seed(0); A=randn(3,2)+ `i randn(3,2); ((A.d A)^-1 A.d) ~== np.linalg.pinv(A)
===============================
True

seed(0); A=randn(3,2)+ `i randn(3,2);                      np.linalg.pinv(A)
===============================
[[ 0.23850346-0.14941741j  0.07430511-0.08088406j  0.20359156+0.05059478j]
 [ 0.06670345+0.11764575j  0.28298303-0.01310121j -0.15924128-0.11027123j]]
---- ClTensor ----

擬似逆行列が (A.d A)^-1 A.d ならば定義「条件1」は下の様に成り立つことが示せます。

擬似逆行列が (A.d A)^-1 A.d のとき、定義「条件1」が成り立つ証明

    Apsd = (A.d A)^-1 A.d

    A Apsd A == A (A.d A)^-1 A.d A  == A (A.d A)^-1 (A.d A) == A

    Apsd A Apsd == (A.d A)^-1 A.d A (A.d A)^-1 A.d == ((A.d A)^-1 (A.d A)) (A.d A)^-1 A.d
                == (A.d A)^-1 A.d == Apsd.

定義「条件2」は下の様に成り立つことが示せます。

擬似逆行列が (A.d A)^-1 A.d のとき、定義「条件2」が成り立つ証明

Apsd=(A.d A)^-1 A.d

(Apsd A).d == ((A.d A)^-1 A.d A).d == 単位行列 == A Apsd

(A Apsd).d == (A (A.d A)^-1 A.d).d == A.d.d ((A.d A)^-1).d A.d == A ((A.d A).d)^-1 A.d == A (A.d A)^-1 A.d == A (A.d A)^-1 A.d == A Apsd

ちなみに、上の式の変形仮定に誤りが入り込んでいないことを下のように数値確認できます。

上の式の変形仮定に誤りが入り込んでいないこの数値確認

seed(0); A=randn(3,2)+ `i randn(3,2); Apsd=(A.d A)^-1 A.d; ((A Apsd).d) ~== ((A (A.d A)^-1 A.d).d), ((A (A.d A)^-1 A.d).d)~==(A.d.d ((A.d A)^-1).d A.d), (A.d.d ((A.d A)^-1).d A.d)~==(A ((A.d A).d)^-1 A.d), (A ((A.d A).d)^-1 A.d)~==(A (A.d A)^-1 A.d), (A (A.d A)^-1 A.d)~==(A (A.d A)^-1 A.d), (A (A.d A)^-1 A.d)~==(A Apsd)
===============================
(True, True, True, True, True, True)


# rank 2 の 3x2 行列のとき、pseudo inverse  以外にも Ax A == E となる Ax が存在する
seed(0); A=randn(3,2)+ `i randn(3,2); (A.t A)^-1 A.t
===============================
[[ 0.19083191+0.01484792j  0.06279178-0.22894183j  0.34142385-0.01398845j]
 [ 0.10843294-0.15421935j  0.33223968+0.22056979j -0.36553262+0.02146981j]]
---- ClTensor ----

seed(0); A=randn(3,2)+ `i randn(3,2); ((A.t A)^-1 A.t) A
===============================
[[  1.00000000e+00 +9.71445147e-17j   0.00000000e+00 +6.59194921e-17j]
 [  1.11022302e-16 +6.93889390e-17j   1.00000000e+00 -5.20417043e-17j]]
---- ClTensor ----

# 正方行列のときは ((A.t A)^-1 A.t) == ((A.d A)^-1 A.d)
seed(0); A=randn(2,2)+ `i randn(2,2); ((A.t A)^-1 A.t) ~== ((A.d A)^-1 A.d)
===============================
True

最初の擬似逆行列の定義は (A.d A)^-1 A.d 定義の拡張とみなせそうです。

特徴的な場合の擬似逆行列の具体例

でもその定義で擬似逆行列が一つだけに限られることが納得できません。さらに擬似逆行列の特徴的な場合の具体例を作ってみましょう。

正方ゼロ行列、行列式==0 の行列での擬似逆行列

全要素が 0 の正方ゼロ行列や、行列式==0 の行列にも擬似逆行列が唯一つ存在します。具体的に Python に計算させてみましょう。

正方ゼロ行列、行列式==0 の行列での擬似逆行列

mt=kzrs(2,2); np.linalg.pinv(mt) 
===============================
[[ 0.  0.]
 [ 0.  0.]]
---- ClTensor ----

mt=kzrs(2,2); mt[0,1]=1; np.linalg.pinv(mt) 
===============================
[[ 0.  0.]
 [ 1.  0.]]
---- ClTensor ----

mt=kzrs(2,2); mt[0,1]=1; np.linalg.pinv(mt) mt
===============================
[[ 0.  0.]
 [ 0.  1.]]
---- ClTensor ----

# 上の三式の PythonSf Open 判コード
mt=np.zeros([2,2]); np.linalg.pinv(mt) 
===============================
[[ 0.  0.]
 [ 0.  0.]]

mt=np.zeros([2,2]); mt[0,1]=1; np.linalg.pinv(mt) 
===============================
[[ 0.  0.]
 [ 1.  0.]]

ベクトルに対してさえ擬似逆行列が存在します。

ベクトルの擬似逆行列

np.linalg.pinv([[1,2,3]])
===============================
[[ 0.07142857]
 [ 0.14285714]
 [ 0.21428571]]

ちなみに、ベクトルの擬似逆行列だからといって np.linalg.pinv([1,2,3]) を numpy は受け付けてくれません。エラーになります。行列に限定しています。

ベクトルと擬似逆行列の積は下の様になります。

ベクトルと擬似逆行列との積

~[1,2,3] np.linalg.pinv([[1,2,3]])
===============================
[ 1.]
---- ClTensor ----

np.linalg.pinv([[1,2,3]]) np.array([[1,2,3]])
===============================
[[ 0.07142857  0.14285714  0.21428571]
 [ 0.14285714  0.28571429  0.42857143]
 [ 0.21428571  0.42857143  0.64285714]]

Vectorの逆行列 * vector を単位行列にすることはできないので上のような 3x3 行列になることは納得できます。では、この 3x3 行列はいったい何者でしょうか。対称行列であることは目視で分かります。ならば直交変換行列で特徴を見出せそうです。固有ベクトル・固有値を見てみましょう。

擬似逆行列との積の固有ベクトル・固有値

eigh(np.linalg.pinv([[1,2,3]]) np.array([[1,2,3]]))
===============================
(ClTensor([ -1.33523813e-16,   1.33523813e-16,   1.00000000e+00])
,ClTensor([[-0.92213325,  0.27971718,  0.26726124],
           [ 0.38339108,  0.75319121,  0.53452248],
           [ 0.0517837 , -0.59536653,  0.80178373]])
)

固有ベクトルが [0,0,1] となっています。何か納得できます。先の擬似逆行列との積の行列を固有ベクトルによる直交変換してみましょう。

擬似逆行列との積行列の固有ベクトルによる直交変換

A=np.linalg.pinv([[1,2,3]]) np.array([[1,2,3]]); mt=eigh(A)[1]; pp(mt^-1 A mt)
[[ 0, 0, 0]
,[ 0, 0, 0]
,[ 0, 0, 1]]
-------- pp --
===============================
None

これでベクトルとその擬似逆ベクトルの積の意味が分かった気がします。単位行列ではないが、直交変換によって見る角度を変えてやることで 0 行列と単位行列に分割できるように擬似逆行列を定義しているのだと。

最初に使った 3x2 ランダム複素行列でも同様な数値実験を行ってみましょう。

3x2 ランダム複素行列における擬似逆行列との積行列の固有ベクトルによる直交変換

A=np.linalg.pinv([[1,2,3]]) np.array([[1,2,3]]); mt=eigh(A)[1]; pp(mt^-1 A mt)
seed(0); A=randn(3,2)+ `i randn(3,2); pp(A np.linalg.pinv(A))
[[           0.607191,  0.31918-0.120161j, 0.230665+0.262658j]
,[  0.31918+0.120161j,           0.703891, -0.10708-0.283986j]
,[ 0.230665-0.262658j, -0.10708+0.283986j,           0.688919]]
-------- pp --
===============================
None

seed(0); A=randn(3,2)+ `i randn(3,2); B=A np.linalg.pinv(A); mt=np.linalg.eigh(B)[1]; pp(mt)
[[          -0.626745,           -0.779224,                   0]
,[ 0.509266+0.191723j, -0.409612-0.154206j,  -0.45115+0.555691j]
,[ 0.368036-0.419083j, -0.296018+0.337077j, -0.351995-0.603134j]]
-------- pp --
===============================
None

seed(0); A=randn(3,2)+ `i randn(3,2); B=A np.linalg.pinv(A); mt=np.linalg.eigh(B)[1]; pp(mt^-1 B mt)
[[ 0, 0, 0]
,[ 0, 1, 0]
,[ 0, 0, 1]]
-------- pp --
===============================
None

今度はユニタリ変換で 0 行列と対角行列に分解できました。

上で A Apsd)[0,-1] が 0 になっているのは、np.randon(..) の非ランダム性によるもの

ちなみに上のユニタリ行列 mt で mt[0,2] 成分がピッタリ 0 になっています。

ピッタリ 0 の確認

seed(0); A=randn(3,2)+ `i randn(3,2); B=A np.linalg.pinv(A); mt=np.linalg.eigh(B)[1]; print "%1.16f"%mt[0,2].real
0.0000000000000000

これは、np.randon(..) の非ランダム性によるものです。seed を 0 以外にしてやれば、ピッタシ 0 はなくなります。

seed(5)にするとピッタリ 0 でなくなる

seed(5); A=randn(3,2)+ `i randn(3,2); B=A np.linalg.pinv(A); mt=np.linalg.eigh(B)[1]; pp(mt)
[[            0.843349,             0.49451,            -0.21029]
,[  -0.281651-0.33363j,   0.308069+0.27618j, -0.405091-0.688537j]
,[ 0.0214572-0.312515j, -0.131677+0.752954j, -0.223593+0.517302j]]
-------- pp --
===============================
None

numpy, scipy の random モジュールは seed(0),seed(1),seed(2) あたりに何らかの非ランダム性があります。今回のように本当にランダムだったら簡単にはおきないような特別の値が出現することに月に一回程度の頻度でも遭遇します。

A A.d を対角化する SU(N)行列と A Apsd を対角化する SU(N)行列

“もしかして A A.d を対角化する SU(N)行列と A Apsd を対角化する SU(N)行列は同じ？” と思い数値実験してみました。

A A.d, A Apsd を対角化する SU(N)行列

seed(0); A=randn(3,2)+ `i randn(3,2); pp(A A.d)
[[           4.19758, 2.46304+0.608492j,  2.82014+1.08622j]
,[ 2.46304-0.608492j,           6.15878, 0.220129-3.99389j]
,[  2.82014-1.08622j, 0.220129+3.99389j,            6.5785]]
-------- pp --

seed(0); A=randn(3,2)+ `i randn(3,2); pp(eigvalsh(A A.d))
[       0,  5.4202, 11.5147]
-------- pp --

seed(0); A=randn(3,2)+ `i randn(3,2); pp(eigh(A A.d)[1])
[[            0.626745,              0.67709,           -0.385668]
,[ -0.509266-0.191723j,    0.293762+0.48276j, -0.311866+0.535982j]
,[ -0.368036+0.419083j, -0.0397718-0.469695j, -0.667917-0.143563j]]
-------- pp --
===============================
None
seed(0); A=randn(3,2)+ `i randn(3,2); pp(eigh(A np.linalg.pinv(A))[0])
[ 0, 1, 1]
-------- pp --

seed(0); A=randn(3,2)+ `i randn(3,2); pp(eigh(A np.linalg.pinv(A))[1])
[[          -0.626745,           -0.779224,                   0]
,[ 0.509266+0.191723j, -0.409612-0.154206j,  -0.45115+0.555691j]
,[ 0.368036-0.419083j, -0.296018+0.337077j, -0.351995-0.603134j]]
-------- pp --

同じではありませんでしたが、なぜか最初の clumn だけはピッタリ一致しています。偶然でこれだけ一致することは一生かかっても御目にかかれないでしょう。

こんなことが発生する理由が分かりません。どなたか分かる方がいらっしゃったらお教えください。

擬似逆行列の私の解釈

現在の私は最初の擬似逆行列の定義を次のように理解しています。

A の逆行列を拡張して Apsd 擬似逆行列を扱えるようにすると A Apsd または Apsd A を単位行列にできなくなる。
A Apsd または Apsd A を単位行列にできなくなっても、適当な直交変換／ユニタリ変換により 0 行列と単位行列に分解できる。
このことと等価なのが最初の Moore-Penrose による逆行列の定義だ

ただし 3 の “このことと等価なのが最初の Moore-Penrose による逆行列の定義だ” は直感で言っているだけで厳密には証明していません。誤りや過不足があったら御指摘願います。

解析関数としての対応関係

f:matrix → pseudo inverse matrix の写像を考えられます。f が正方行列の逆写像であるとき、f は連続であり、多変数の解析関数で表される関係にあります。でも擬似逆行列への写像が入り込んでくると、ここでカタストロフィックな変化が発生してきます。

~[[0,1,2],[3,4,5],[6,7,8]] 行列の行列式は 0 であり逆行列は存在しません。でもこの擬似逆行列は存在します。

~[[0,1,2],[3,4,5],[6,7,8]]の擬似逆行列

mt=~[[0,1,2],[3,4,5],[6,7,8]]; np.linalg.pinv(mt)
===============================
[[ -5.55555556e-01  -1.66666667e-01   2.22222222e-01]
 [ -5.55555556e-02   2.01227923e-16   5.55555556e-02]
 [  4.44444444e-01   1.66666667e-01  -1.11111111e-01]]
---- ClTensor ----

この (0,0) 成分を複素領域で振ってみたとき、擬似逆行列の (0,0) 成分がどのうよに変化するかを次のように可視化できます。

mt[0,0] を複素領域で振ったときの擬似逆行列の (0,0) 成分の変化

mt=~[range(3 3),complex].reshape(3,3); def g(z):mt[0,0]=z; f=λ z:g(z) or np.linalg.pinv(mt)[0,0]; plot3dGr(f,[-1,1],[`i,-`i])
index:(24, 24)  max: 34.6482  : (-24.5-24.5j)
index:(49, 0)  min: 0.707107  : (0.5-0.5j)
===============================
None

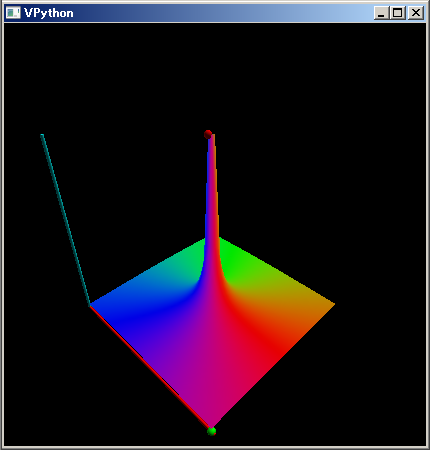
この関数は z=0 の回りで一次の極を持っています。位相が 360 度回転し無限大に発散していることから分かります。ただし擬似逆行列の 00 成分は z=0 の位置で -1.55555.. == -5/9 の有限値を持ちます。

同様に (1,1) 成分、(2,2) 成分がどのように変化するかも見てみましょう。

(1,1) 成分、(2,2) 成分の変化

mt=~[range(3 3),complex].reshape(3,3); def g(z):mt[0,0]=z; f=λ z:g(z) or np.linalg.pinv(mt)[1,1]; plot3dGr(f,[-2,2],[2`i,-2`i])
index:(24, 24)  max: 35.6035  : (-25.8333333333-24.5j)
index:(43, 24)  min: 0.0371315  : (-0.00997566909976-0.0357664233577j)
===============================
None

mt=~[range(3 3),complex].reshape(3,3); def g(z):mt[0,0]=z; f=λ z:g(z) or np.linalg.pinv(mt)[2,2]; plot3dGr(f,[-1,1],[`i,-`i])
index:(24, 24)  max: 35.6035  : (-25.8333333333-24.5j)
index:(43, 24)  min: 0.0371315  : (-0.00997566909976-0.0357664233577j)
===============================
None

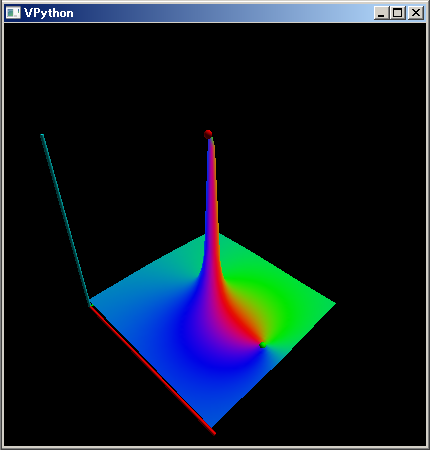
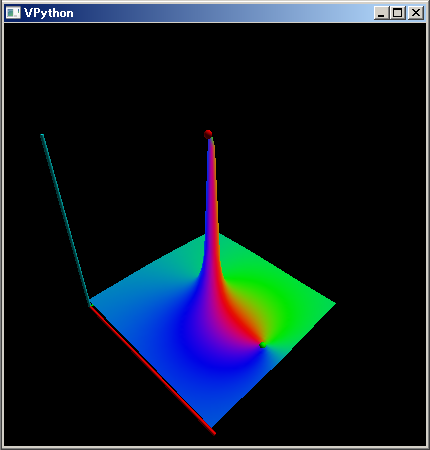
こっちの分布では実数軸の 1.5 近辺、 0.8 近辺にゼロ点も出現しています。実際の擬似逆行列では (1.1) 成分のみが 0 なのですが。

f:matrix → pseudo inverse matrix の写像では、逆行列から擬似逆行列に移る箇所で無限大を含む変化か発生し有限値になる現象は一般的に起きているようです。現在のところ大きな不連続性があるとしか、私には分かりません。

擬似逆行列と最小誤差

↑ 推測した aG vector に perturbation を 100 回 random に与えて、つねに generalized inversed のときより誤差が増えるのならば、最小にする推定だと証明できたとみなせる。

a=[1,2,3]; seed(0); N=10; vX=randn(N); mtMsrd=np.c_[X^2(vX), X(vX), [1]*N]; mtMsrd MsrdyMsrd=(a[0]X^2+a[1]X+a[2]) randn( a=[1,2,3]; seed(0); N=10; =randn(N); xMsrdyMsrdyMsrd=(a[0]X^2+a[1]X+a[2]) randn(

np.c_[ [1,2,3],[4,5,6] ]

[[1 4] [2 5] [3 6]] np.c_[~[1,2,3],~[4,5,6] ] =============================== [[ 1. 4.] [ 2. 5.] [ 3. 6.]] ↑ not ufunc

a=[1,2,3]; seed(0); N=10; vX=randn(N); mtMsrd=np.c_[(X^2)(vX), X(vX), [1]N]; mtMsrd a=[1,2,3]; seed(0); N=10; vX=randn(N); mtMsrd=~[np.c_[(X^2)(vX), X(vX), [1]N]]; mtMsrd =============================== [[ 3.11188068 1.76405235 1. ] [ 0.16012579 0.40015721 1. ] [ 0.95792804 0.97873798 1. ] [ 5.02160233 2.2408932 1. ] [ 3.48777285 1.86755799 1. ] [ 0.95507205 -0.97727788 1. ] [ 0.902668 0.95008842 1. ] [ 0.022909 -0.15135721 1. ] [ 0.01065413 -0.10321885 1. ] [ 0.16859113 0.4105985 1. ]] —- ClTensor —- # a=[1,2,3] のとき y=a[0] x^2 + a[1] x + a[2] で N 回データを測定した mtMsrd, yMsrd をつくる a=[1,2,3]; seed(0); N=10; vX=randn(N); mtMsrd=~[np.c_[(X^2)(vX), X(vX), [1]*N]]; yMsrd = mtMsrd a; yMsrd =============================== [ 9.63998537 3.96044021 5.91540401 12.50338873 10.22288883 2.00051629 5.80284484 2.72019459 2.80421643 3.98978813] —- ClTensor —-

作った mtMsrd, yMsrd から a パラメータを pseudo inverse で求める。a=[1,2,3] が再現する。

a=[1,2,3]; seed(0); N=10; vX=randn(N); mtMsrd=~[np.c_[(X^2)(vX), X(vX), [1]*N]]; yMsrd = mtMsrd a; np.linalg.pinv(mtMsrd) yMsrd =============================== [ 1. 2. 3.] —- ClTensor —-

yMsrd+ノイズから a パラメータを pseudo inverse で求める。a=[1,2,3] から少しだけずれる

a=[1,2,3]; seed(0); N=10; vX=randn(N); mtMsrd=~[np.c_[(X^2)(vX), X(vX), [1]*N]]; yMsrd = mtMsrd a + 0.1 randn(N); np.linalg.pinv(mtMsrd) yMsrd =============================== [ 0.98306723 2.02911852 3.04363362] —- ClTensor —-

mtMsrd, yMsrd のペアに対して擬似逆行列から推定した aGsd parameter を使った、誤差の自乗評価値を求める。

a=[1,2,3]; seed(0); N=10; vX=randn(N); mtMsrd=~[np.c_[(X^2)(vX), X(vX), [1]*N]]; yMsrd = mtMsrd a + 0.1 randn(N); aGsd=np.linalg.pinv(mtMsrd) yMsrd; normSq(yMsrd - mtMsrd aGsd) =============================== 0.0425676371105 ↑ 誤差の自乗評価値 ↑ ノイズのぶんだけ a==[1,2,3] からずれてくる。 ↑ ノイズがなかったら aGsd == [1,2,3] のなり、誤差の自乗評価値も 0 になる。 ↑ aGsd=[ 0.98306723 2.02911852 3.04363362] からずれたとき、常に誤差の自乗評価値は 0.0425676371105 より大きくなるはず。 ↑ 最少値だったのだから

aGst==~[ 0.98306723, 2.02911852, 3.04363362] から少しずらしたときの誤差自乗評価値を計算してみる

δ=0.001; a=[1,2,3]; seed(0); N=10; vX=randn(N); mtMsrd=~[np.c_[(X^2)(vX), X(vX), [1]*N]]; yMsrd = mtMsrd a + 0.1 randn(N); aGsd=np.linalg.pinv(mtMsrd) yMsrd; normSq(yMsrd - mtMsrd (aGsd+δ randn(3))) =============================== 0.0427678823863 ↑0.0425676371105 より少し多い

aGst==~[ 0.98306723, 2.02911852, 3.04363362] から少しずらしたときの誤差自乗評価値を 100 回計算して 0.0425676371105 より常に大きいことを確認する

何かの間違いで常に同じ評価値になっていたかもしれない。評価値の差を明示的に出力させる。

δ=0.001; a=[1,2,3]; seed(0); N=10; vX=randn(N); mtMsrd=~[np.c_[(X^2)(vX), X(vX), [1]*N]]; yMsrd = mtMsrd a + 0.1 randn(N); aGsd=np.linalg.pinv(mtMsrd) yMsrd; [ normSq(yMsrd - mtMsrd (aGsd+δ randn(3)))-0.0425676371105 for _ in range(100) ] =============================== [0.00020024527581327667, 2.6339302337675952e-05, 2.1542512584120377e-05, 0.00013757896148604287, 0.00020308859974140642, 7.4800871225244592e-05, 4.2190521970839057e-05, 0.00016786102706704831, 6.9286991437676748e-05, 8.4051036943894042e-06, 3.8549069422938453e-05, 5.7679643961972005e-05, 2.4925916614071397e-06, 3.3791158547472055e-05, 0.00013660112418934639, 6.4627576512779616e-05, 2.5015147745569011e-05, 1.693380131757849e-05, 7.6498360365231943e-06, 2.5667129547726764e-05, 2.0970700728165093e-05, 3.0738382941250531e-05, 3.6292686524483364e-05, 8.2942399220034546e-05, 3.4742561613787526e-05, 9.472475351823828e-05, 5.9377199159466043e-05, 0.00014986483174320858, 1.8029796009788601e-05, 4.4013376935464477e-05, 0.00021606352362006642, 0.00020642784703849004, 5.7470814312426954e-05, 3.7222898830152618e-05, 3.474013751431082e-05, 2.120371106698743e-05, 2.421011679329399e-05, 3.7681084799345843e-06, 4.2640336386234878e-06, 1.2777621410581252e-05, 7.575226361501014e-05, 0.00023740260328107554, 4.1658835617408574e-05, 1.6420825469459777e-05, 7.1025409252523097e-05, 1.9353795213769565e-05, 0.00011533633593532877, 0.00029375668207926031, 6.8922290150472132e-05, 4.2715603456068563e-05, 9.2661683675832052e-05, 5.067983935053838e-05, 8.3566512388499881e-05, 2.6947515169344072e-05, 0.00013464876480503984, 0.00022827556699241136, 2.2685472521273564e-05, 8.1518924250553737e-06, 2.5664781297396466e-05, 0.00028250543515520588, 8.1070348242409662e-06, 2.7279134112878634e-05, 6.4936582888641681e-06, 1.2753784976643479e-05, 9.6448152383452057e-06, 5.4507233764045093e-06, 0.00019522531465039628, 1.1008590610817048e-05, 0.00010672885176467306, 2.2662555964475528e-06, 0.00016836951519923204, 7.46132982078207e-06, 3.2191657094803039e-05, 5.2479797520710303e-06, 7.6385155901442792e-06, 4.2245276001703913e-05, 0.00010147809101017369, 1.8625776647851477e-05, 3.7212236255176889e-05, 0.00020297689925417167, 0.00013235618114681297, 5.5225542010366169e-05, 1.176047940641689e-05, 5.7262240405545062e-05, 0.00019235974990634841, 2.4854796849688165e-06, 6.8386054831365284e-05, 7.8945498832777572e-05, 1.0693635797878742e-05, 0.00019742643032782947, 3.1598460623824542e-05, 3.8152600815008486e-05, 5.2702148653493985e-06, 2.2310000127992446e-05, 6.8587940717790286e-06, 0.00012974264849863193, 1.6708992974588666e-05, 1.188589791375344e-05, 6.1819160443107868e-06, 6.1332809720426873e-06]

# aGst==~[ 0.98306723, 2.02911852, 3.04363362] から少しずらしたときの誤差自乗評価値を 10000 回計算して 0.0425676371105 より常に大きいことを確認する
δ=0.001; a=[1,2,3]; seed(0); N=10; vX=randn(N); mtMsrd=~[np.c_[(`X^2)(vX), `X(vX), [1]*N]]; yMsrd = mtMsrd a + 0.1 randn(N); aGsd=np.linalg.pinv(mtMsrd) yMsrd; all([ normSq(yMsrd - mtMsrd (aGsd+δ randn(3)))>0.0425676371105 for _ in range(10000) ])
===============================
True ↑ 一万個の True だけのリストを見ても見逃すだけなので all([True, True, ... , True]) であることを確認した。

数学では抽象的で厳密な証明が重視されます。その意味も理由も分かります。でも擬似逆行列の抽象的で厳密な証明を理解・構築する前に、上で検討したような擬似逆行列についての雑多な知識を網羅することの方が優先するのが科学だと私は主張します。皆様は如何でしょうか。

wikipedia 3

Pythonsf Pseudo Inverse Jpn pysf wikipedia

概要