kkRGB 複素平面 x 複素平面の表示

四次元表示となってしまう複素関数の複素数値分布の様子を、コンピュータの RGB 表示を活用して解りやすく表示することを提案します。

今までは複素解析関数や量子力学の波動関数など、複素数値をとる関数をグラフ表示させるときは、絶対値のグラフ表示だけで代用したり、実数値と虚数値の二つのグラフで表示させたりしていました。これらから複素数値の分布をイメージするのが困難でした。

現在のパソコンにとっては RGB カラーを 8^3 bit 表示することは簡単です。これを複素数値の位相回転の表示に利用してやれば、複素関数値の四次元分布を直感的に表示することが可能になります。すなわち複素数値を次のような kkRGB 複素数値表示と名付けた RGB カラー・マップで表示することを提案します。

kkRGB の機能は ClCplxColor Python クラスとして pysf\vsGraph.py ファイルに実装されています。2013.06.21 現在 pysfOp 版には移植されていません。

kkRGB 複素数値表示

kkRGB 複素数値表示では、二次元の複素平面に配置される複素数値を、下のような複素平面に対応させた RGB colour の一つのピクセルで表示します。

より詳細には以下のように表示します。

1. 複素数の絶対値が limit 値よりも大きいときは、白(R==0xff, G==0xff, B=0xff) で表示します。
2. 複素数の絶対値が boundory 値よりも大きいときは、複素数平面の四象限に黄色 (R=255, G=255, B=255)、黄緑(R=120, G=255, B=120)、空色(R==0, G==255, B=255)、赤紫(R=255, G==0, B=255) の四色を配分させ、複素数値を四値で段階的に変化させデジタル表示します。
3. 複素数の絶対値が boundary 色境界より小さいときは RGB の三原色の比率により複素数の回転角を表し、RGB の強さにより複素数の絶対値を表します。すなわち絶対値 0 を黒とし、そこから Boundary 色境界までを連続的に変化させた RGB アナログ表示します。

render2dRGB(..) 関数を使った kkRGB 表示コード

info(render2dRGB)
 render2dRGB(mtrxAg, boundary=1.0, limit=10.0, blReverse=False, blBoth=False,
             fileName='kkRGB', blDisplay=True, blMax=False)

' Render a complex value distribution with kkRGB color for matrix argument
        rendered figure is saved at kkRGB.jpg file as a default
    e.g.
vc=klsp(-3,3,300); f=`X^3+`X^2+`X+1; dct={};for idx,(x,y) in enmitr(vc,vc):dct[idx]=f(x+`i y); render2dRGB(dct)
    '
===============================
None

長方形の複素数値分布を、行列データとして render2dRGB(..) 関数に与えることで、対応する kkRGB.jpg ファイルをカレント・ディレクトリに生成します。start kkRGB.jpg コマンドを続けて実行するので、Windows では jpg 拡張子に対応させてあるプログラムで kkRGB 複素数値分布が表示されます。

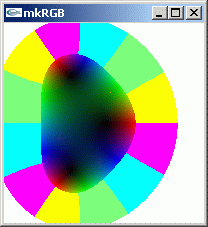
上の kkRGB 表示画像の jpg ファイルは下の PythonSf one-liner で作れます。

vc=klsp(-1,1,300); f=`X  ; dct=[[f(x+`i y) for y in -vc] for x in vc]; render2dRGB(dct,0.6, 0.9)

下の PythonSf one-liner により z + 2z^2 + 3z^3 多項式の複素数値の分布を -1+i, 1+i, 1-i, -1-i の四点で囲まれた複素領域について 200 x 200 サイズの kkRGB.jpg ファイルを作成します。

z,vc=`X,klsp(-1,1,200); f=z + 2z^2 + 3z^3; dct=[[f(x+`i y) for y in -vc] for x in vc]; render2dRGB(dct, 0.5, 5.0)

三根の周りで位相が 360度回っていること、全体で 3 x 360度位相が回っていることが分かります。三根から離れるにしたがって、多項式関数値の絶対値が増えていくこと、等絶対値線が歪んだ同心円の形から円に近づいていくことが分かります。また等位相線と等絶対値線は直交していることも分かります。(これは全ての解析関数について成り立ちます。)

通常だと四次元になってしまう解析関数の複素平面状の複素数値分布が kkRGB 表示によってリアルにイメージできます。上の PythonSf one-liner は f= ... の右辺式を変えてやるだけで、任意の解析関数の kkRGB 表示を生成できます。真性特異点をもつやリーマン面を持つ解析関数などの kkRGB 表示をさせてやるだけで結構遊べます。お試しください。