■■ 初めに
Python sf は計算に特化したソフトです。普段メモ書きしている数式を、そのまま実行できることを理想としています。Python sf は 計算ソフトの L.L.(Light weight Language) です。大部分のエンジニア・研究者が行っている日常計算の九割以上を Python sf のワンライナー数式で扱える・扱えるようにカスタマイズできるでしょう。
Python sf では、多くの場合デバッグなしでエンジニア・研究者が知りたい計算結果の値を得られます。知りたいグラフ表示結果を得られます。エンジニアや研究者がコンピュータに計算させるために、プログラム・コードを書き、そのコードのデバッグをしていたのでは回り道すぎます。そうです。常日頃メモ書きしている数式のまま、コンピュータに計算させるのならばデバッグを省けます。ワン・ライナーの Python sf 式を書くだけで、コンピュータに計算させられます。Python sf ワンライナーには if then else 文を入れません。逐次処理を並べるだけです。ですからデバッグするようなミスは殆ど入りこみません。
例えば、原点にある電荷が作る、(1,2,3) 位置の電場ベクトル値を次の Python sf 式で計算できます。
( (~[`X,`Y,`Z])/norm(~[`X,`Y,`Z]) )(1,2,3) =============================== [ 0.26726124 0.53452248 0.80178373] ---- ClTensor ----
下は r=[1,0,0] にある電荷が作る、(1,2,3) 位置の電場ベクトル値です。
r=[1,0,0];( (~[`X,`Y,`Z]-r)/norm(~[`X,`Y,`Z]-r) )(1,2,3) =============================== [ 0. 0.5547002 0.83205029] ---- ClTensor ----さらに発展させ、[-1,0,0],[1,0,0]の位置に電荷を持つ双極子が作る電場ベクトルの div 値,rot 値 および 3D 分布を下の Python sf 式でコンピュータで計算し、また描かせられます。
# divergence value at (0,0,0) f=λ r:(~[`X,`Y,`Z] - r)/norm(~[`X,`Y,`Z] - r)^3; `div(f([1,0,0])-f([-1,0,0]) )(0,0,0) =============================== 0.0 # rotation value at (0,0,0) f=λ r:(~[`X,`Y,`Z] - r)/norm(~[`X,`Y,`Z] - r)^3; `rot(f([1,0,0])-f([-1,0,0]) )(0,0,0) =============================== [[ 0. 0. 0.] [ 0. 0. 0.] [ 0. 0. 0.]] ---- ClTensor ---- # rot はベクトルではなく反対称行列で表します # 一般の N 次元ベクトル関数でも rot を計算させるためです # dipole 電場分布の 3D 表示 v=klsp(-2,2,8);f=λ r:(~[`X,`Y,`Z] - r)/norm(~[`X,`Y,`Z] - r)^3;kqvr3d( list(mitr(v,v,v)),f([1,0,0])-f([-1,0,0]) );kmshw()
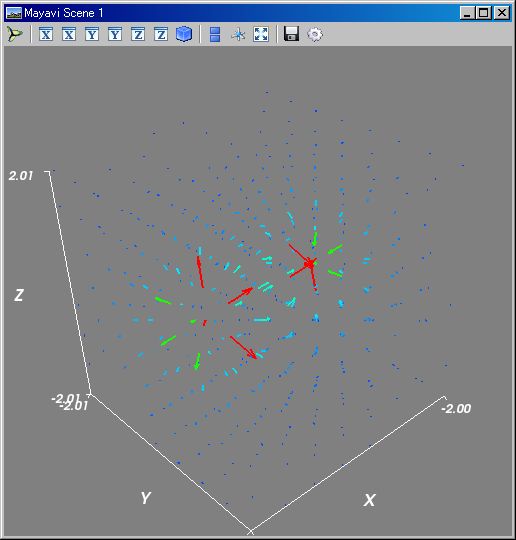
ここで行っていることは、「行列けベクトル生成:~[...]」、「引数タプルから 0 番目の値を取り出す関数:`X」... などの Python sf 要素を並べ組み合わせて逐次処理させているだけです。線形代数などの数学理論体系が if then else 無しでの記述を可能にします。「x > 0」といった場合分け無しでの記述を可能にしてくれます。これらの逐次処理を並べるだけのコードにはバグが入り込む可能性は殆どありません。常日頃慣れ親しんでいる数式:コードを逐次並べるだけで、デバッグなしでエンジニア・研究者が知りたい値を計算し、見たい 3D グラフを表示させています。
ここで行っているベクトル処理が Python sf の基本要素で行えている点に注目してください。ベクトル解析パッケージのような専用のものを導入するのではなく、シンボル処理をしているのでもなく、Python の数値関数と行列演算と数値微分を組み合わせて行っていることに注目ください。Python, Python sf の記述性の高さに注目ください。
Python sf は既にある Python ライブラリ・パッケージの蓄積を活用することで、Matlab, Mathematica と同等以上の機能を持ちます。scipy, sympy, vpython の三つのパッケージは、Python sf を動かすために必須です。scipy の行列を中心とする数値計パッケージトは Matlab に近い機能を持ちます。sympy パッケージは、シンボリックな数式処理を可能にします。vpython は、高速な 3D グラフ表示のために使っています。
この三つのライブラリ・パッケージを使い、Python 計算プログラム・コードを書きデバッグしているだけでは数値計算ソフトの L.L とは言えません。Python sf では 10000 行を超えるラッパを被せています。これにより Python のアッパー・コンパチでありながら、計算式を短く記述できる、計算ソフトの L.L. に仕上げられました。
┌────────────────┐ │ Python sf │ │ sfPPrcssr 一万行以上の │ ┌────────────────────┐ │ Pre - processor │ │scipy: Matlab 相当の数値計算パッケージ │ │ │ │sympy: シンボリック数式処理パッケージ │ │ sfFnctns:.行列の拡張 │ │vpython:3D 表示 │ │ basicFnctns │ │mlb:mayavi 2d/3d 表示パッケージ │ │ kNumeric 微分・積分拡張 │ └────────────────────┘ │ vsGraph 簡便なグラフ表示│ ┌────────────────────┐ │ rational 有理式 │ │既存のーザー側で用意する pythonライブラ │ │ customize.py │ │リ・パッケージ │ │ sfCrrntIni.py │ └────────────────────┘ │ ユーザー・カスタマイズ │ ┌────────────────────┐ │ octn.py │ │ユーザー側で開発する python │ │ 八元数 │ │モジュール・パッケージ │ │ Bool 体 │ └────────────────────┘ │ GF(2^8) Galois 体 │ │ Zp, Sn │ │ │ │ tlRcGn │ │ 無限数列 │ │ 末尾再帰 │ │ │ │ kre 正規表現 │ │ │ │ kv kVerifier test library │ │ │ └────────────────┘
~[...] で行列やベクトルを生成したり、漢字 :λ を使って Python lamba 構文を表現できるのは pre-processor のおかげです。これにより、Python の名前空間とは独立したユーザー・カスタマイズ可能な変数・関数・演算子を使えるようにしました。数学で多用するギリシャ文字や特殊記号を使えるようにしました。ユーザーの扱う分野にカスタマイズした変数・関数・演算子記号を扱えるようにしました。行列やベクトルを記述する記号を導入できました。数式記述での積演算子 * の省略を可能にしました。
scipy は素晴らしい数値演算パッケージですが、実際に使う上では多くの不満が出てきます。ベクトル・行列計算を普段メモ書きする数式までには簡略化できません。Bool 体などの一般体を要素とする行列も扱えません。微分や多項式などの扱いにも不満が出てきます。計算結果のグラフ表示も、できるだけ簡便に行わせたくなります。これらの不満をプリプロセッサと sfFnctns.py などの追加モジュールを設けて解消しました。
数学ソフトはユーザーごとにカスタマイズして使うソフトです。ユーザーによって必要とされる関数、変数・定数や その意味・記述方法は大きく異なります。理論物理学者と電気回路技術者では、同じ加減乗除算記号を使いますが、その計算内容は全くの別物です。必要される計算機能も共通部分より異なる部分のほうが多いでしょう。この違いの問題は、プリプロセッサを前提とするカスタマイズ専用ファイル:customize.py を設けることで解決しています。
また行列を拡張して、整数・実数・複素数以外の一般の体・環の要素からなる行列も扱えるようにしました。有理式からなるインピーダンス行列・Bool 体多項式なども扱えるようにしました。関数を要素とするベクトルや行列さえも扱えるようにしました。
Python sf は開かれたソフトです。Python で扱える機能の全てを Python sf でも扱えます。Pytho sf の配布ソフトだけでは不足している数学機能があるときは、Python sf とは無関係に全世界で開発されている様々の Python ライブラリ・パッケージをユーザー側でインストールして使ってください。Python sf はアッパー・コンパチであり、それらと矛盾することなく使えます。
また python 自体がユーザー側で容易に機能を追加できる言語でもあります。例えば Python sf が公開している octn.py ソース・ファイルにある Bool 体クラス BF、有限整数体 Zp クラスは 100 行、150 行で書かれています。別の体が必要なときは、ユーザー側で作ってください。octn.py にある BF クラスでの様に、__add__, __mul__ などの四則演算関数を定義してやるだけで、Python sf 側で用意している多項式や行列を勝手、ユーザー作った体クラスのインスタンスを操作できます。
高機能でありながらユーザー・カスタマイズ可能な開かれた L.L. 計算ソフト Python sf を是非とも試してみてください。
python で行列・数値計算なんて遅いんでしょ? <== 十二分に早いよ!
インタプリタである python による数値計算なんて遅くて使い物にならないと思われる方がいるかも知れません。でも それは誤りです。素人の C 実装による計算プログラムでは python nympy の計算スピードに勝てないことのほうが多いでしょう。
Python numpy の行列計算では linpack ライブラリが使われます。カリカリにチューニングされた C の行列計算ライブラリーです。その行列計算速度は、殆ど C で書いた linpack の速度に匹敵します。Python numpy の行列計算で動いているのは、インターフェース部分だけを Python に合わせた C で書かれたコードだからです。
論より証拠! 計算時間を実測してみましょう。
//@@
import numpy as sc
import numpy.linalg as sl
randn = sc.random.randn
#N=1000
N=300
import time
startTimeAt = time.time()
mt=randn(N,N) # make NxN matrix which element has normal randam value
print "time to make %d x %d random value matrx :"%(N,N),time.time() - startTimeAt
startTimeAt = time.time()
mtInv= sl.inv(mt)
print "time to calculate %d x %d matrx invers:"%(N,N),time.time() - startTimeAt
startTimeAt = time.time()
mt2= sc.dot(mt, mtInv)
print "time to multiply %d x %d with the inversed matrx:"%(N,N),time.time() - startTimeAt
print mt2
//@@@
実測値: using MSI net book U115
python temp.py
time to make 300 x 300 random value matrx : 0.0160000324249
time to calculate 300 x 300 matrx invers: 0.266000032425
time to multiply 300 x 300 with the inversed matrx: 0.140000104904
[[ 1.00000000e+00 -1.99840144e-15 2.10942375e-14 ..., -1.66533454e-15
-1.42108547e-14 -8.88178420e-16]
[ 9.99200722e-16 1.00000000e+00 -1.17683641e-14 ..., -2.13717932e-15
-6.66133815e-15 -4.99600361e-16]
[ -1.38777878e-15 2.22044605e-15 1.00000000e+00 ..., -2.27595720e-15
4.44089210e-15 6.43929354e-15]
...,
[ -2.77555756e-16 1.33226763e-15 -1.50990331e-14 ..., 1.00000000e+00
-1.15463195e-14 3.55271368e-15]
[ 3.10862447e-15 -1.33226763e-14 2.48689958e-14 ..., -6.21724894e-15
1.00000000e+00 -3.77475828e-15]
[ -1.22124533e-15 -1.33226763e-15 5.77315973e-15 ..., 2.55351296e-15
-4.44089210e-15 1.00000000e+00]]
デスクトップ・パソコン CPU:E7500 だと次のような計算時間です。「一回目」はパソコン立ち上げ直後での実行時間です。二回目は CPU キャッシュに Python sf で使うコードが書き込まれた後の実行時間です。
# E7500 一回目
python temp.py
time to make 300 x 300 random value matrx : 0.0160000324249
time to calculate 300 x 300 matrx invers: 0.31299996376
time to multiply 300 x 300 with the inversed matrx: 0.0150001049042
[[ 1.00000000e+00 1.59872116e-14 -2.77555756e-16 ..., 5.68434189e-14
3.37507799e-14 -1.24344979e-14]
[ 8.88178420e-16 1.00000000e+00 -6.66133815e-16 ..., 7.10542736e-15
-5.32907052e-15 6.66133815e-16]
[ 2.39808173e-14 2.30926389e-14 1.00000000e+00 ..., 4.61852778e-14
-2.66453526e-14 -2.26485497e-14]
...,
[ -5.28466160e-14 -1.15463195e-14 -6.66133815e-16 ..., 1.00000000e+00
1.46549439e-14 -1.36557432e-14]
[ 1.97619698e-14 5.17363929e-14 1.83186799e-15 ..., 4.26325641e-14
1.00000000e+00 9.65894031e-15]
[ -5.01820807e-14 -3.77475828e-14 6.66133815e-15 ..., 1.55431223e-13
1.82076576e-14 1.00000000e+00]]
copy c:\#####.### temp.py /y
1 個のファイルをコピーしました。
# E7500 二回目
python temp.py
time to make 300 x 300 random value matrx : 0.0
time to calculate 300 x 300 matrx invers: 0.0309998989105
time to multiply 300 x 300 with the inversed matrx: 0.0
[[ 1.00000000e+00 3.77475828e-15 9.54791801e-15 ..., -3.99680289e-15
2.22044605e-15 5.99520433e-15]
[ -2.64233080e-14 1.00000000e+00 1.15463195e-14 ..., -3.86357613e-14
-2.17603713e-14 -2.28705943e-14]
[ -1.59872116e-14 -1.68753900e-14 1.00000000e+00 ..., 1.77635684e-14
2.13162821e-14 2.57571742e-14]
...,
[ 3.99680289e-15 2.66453526e-15 -8.88178420e-16 ..., 1.00000000e+00
-3.10862447e-14 1.15463195e-14]
[ -7.32747196e-15 -1.06581410e-14 9.88098492e-15 ..., 5.55111512e-15
1.00000000e+00 1.55431223e-15]
[ -5.21804822e-14 -2.86437540e-14 6.21724894e-15 ..., 4.44089210e-16
-2.84217094e-14 1.00000000e+00]]
■■ python sf のインストール:python(x,y) Distribution
wPython sf のインストールは、既に scipy, sympy, vpython, mayavi package がインストールされている環境にあるのならば非常に簡単です。
- Python sf が配布している pysf ディレクトリをカレント・ディレクトリまたは python の Lib\site-packages ディレクトリに
- sfPP.py をカレント・ディレクトリに置く
Python sf 評価版では、その他に Vc7VrfyMDdRt10D.zip キー・ファイルをカレント・ディレクトリに置く必要があります。
scipy, sympy, vpython, mayavi package がインストールされている環境にある方むけに、Python sf ポータブルの配布をここ:psff_095c.zip:5.5MBに置いてあります。この zip ファイルの中の sf_v095c 以下のファイル全部をユーザーの任意のディレクトリに置けば、それだけで Python sf は動きます。sf_v095c ディレクトリ名は自由に変更可能であり、また USB メモリ上に置くことも可能です。
Python 自体をインストールしていない方、または scipy, sympy, vpython, mayavi package をインストールしたくない方向けに、これらを全て含んだ Python sf のポータブル版もここ:pysf_095cAll.zip:131MBに置いてあります。
この機会に scipy, sympy, vpython, mayavi package も含めて Python をインストールしてみようとされる方には、python(x,y) Distribution を薦めます。先のの四の package が含まれているからです。
なお、mayavi package を使うのは ベクトル分布表示など限られています。グラフ表示などの pylab や vpython などで表示できる大部分の場合は mayavi なしで済みます。
■■ python sf のインストール:Enthought Distribution
Windows Python 2.6/2.5 を前提に、テストしています。Python 2.4 では、一部問題がでます。残念ですが、2010.04.10 現在の評価版では Linux 向けの配布を未だ行っていません。
■ インストール方法
Python sf ではインストーラを設けていません。pythonSf095?.zip を解凍して、できたディレクトリ mtCm をカレント・ディレクトリとすれば動作するからです。mtCm の名前をユーザーの望む名前に変更しても問題ありません。
レジストリや環境変数を操作することもありません。アンインストールは mtCm ディレクトリを消去するだけです。気軽に試してください。
ただし、下の scipy, sympy, vpython の三つ python package がインストールされていることを前提とします。現在の Ehthought の Python distribution には sympy が含まれているので、python をインストールしていない方は、下の二つをインストールすることで Python sf を動かさせるようになります。
- EPD for Python2.6;;http://www.enthought.com/products/epd.php
- Visual5 ;;http://vpython.org/index.html
別に Enthought の ディストリビューションではなく、別の python2.6(2.5 でも可), scipy, vpython をインストールすれば動きます。
ただし Enthought2.6 packge のインストール後に vpython をインストールするとき numpy をインストールさせないように注意してください。Enthought の方が新しいバージョンの numpy を使っています。vpython の numpy をインストールすると Enthought Python の numpy/scipy 動作の一部がおかしくなります。
■ インストール後のテスト
pythonSf095?.zip を解凍し、また scipy, sympy, vpython が動作する状態になったら、解凍先のディレクトリに移り vfPP.bat を実行すると、現在までに蓄積されたテストが実行されます。
解凍先の kv ディレクトリに kVerifeir テスト・ライブラリの Python sf 専用にしたものが入っています。
■ Python sf 評価版の制限
Python sf の評価版であっても機能の制限は一切ありません。
ただし評価版では動作開始時に無条件に 5秒遅らされ、コピーライト表示されます。
またカレント・ディレクトリにVc7VrfyMDdRt10D.zip ファイルをキーファイルとして置いておく必要があります。このファイルがないと Python sf が動きません。
■ Enthought ライセンスと python sf
Python sf は、ビジネス・ユースを許容している scipy, sympy, vpython のモジュールの存在を前提しているだけであり、膨大な Enthought 配布ソフトを必要としません。たんに Ehthought 配布を利用するとインストールが一番簡単になるために、 Enthought 配布を前提とした説明を書いているだけです。
Python sf をビジネス用途で安価に配布したいときは、無償の Python(x,y) ディストリビューションを使うことを勧めます。
なお、Enthought のディストリビューションはアカデミック・ユース以外は有償のように見えてしまうかもしれませんが、ここに次のように書かれています。「The real intent of the license is to provide a service for those firms who plan on using our bundle of software (EPD) in their commercial operation. Academic and hobbyist use is, and will remain, free.」商売にしないのならばアカデミック・バージョンを使っていいと解釈できると思います。
むしろ、Enthought distribution を多くの人たちに評価してもらい、Enthought.chaco/traits など Engthought が開発したソフトを積極的に活用したビジネスの機会を作り出し、Enthougt にライセンス料を払ってもらうことを目指しているのだと思います。私も そのような機会が増えること願っています。
■■ Python sf の概観・実行
Python sf はコマンド・ラインで動かすソフトです。ユーザーが日常使っているエディタのコンソール・モードに組み込んで使うと便利です。マウスを使うのは 3D グラフ表示結果を視点を変えてみるときなどに限られます。
マウス操作になれた方には違和感があろうかとも思います。この機会にコマンド・ライン操作に慣れることを勧めます。計算処理のためのコンピュータ操作の過程でマウス操作が有利な個所は少ないからです。キーボード上の指先操作で、コンピュータに Python sf 式を与えるのに IDE は必要ありません。IDE よりも手馴れたエディタを使えることの方が重要です。
■ 評価版での機能制限
pythonSf095?.zip で配布している Python sf 評価版の機能は製品版と全く同じです。機能の制限ではなく、動作を遅くさせています。全ての計算で、四秒のディレーを挿入しています。四秒のディレーさえなければ Python sf を使えるとの評価をいただけましたら、有償版の Python sf に切り替えてください。
■ ワンライナーでの実行
Python sf は、テキスト・エディタでメモ書きしているままで計算させることを理想としています。できるだけワンライナーの計算式で実行できるように作ってあります。線形代数を考えれば分かってもらえると思いますが、整理・完成された数学は計算させるときに場合分けすることが少なくなるように出来上がっています。研究・設計で出てくる多くの数学計算は、if then else を必要としません。多くの方にとって、大多数の計算がワンライナーで済んでしまうと思います。というより、ワン・ライナーでできる程度の複雑さの計算を積み重ねで思考を組み立てていくことしかできないのであり、そのように公式や関数を作っていくはずです。
ワンライナーで計算させられることに拘る理由は、計算のためにプログラムやデバッグをしないためです。研究や設計のために、計算ソフトを実行させるのであり、そのために必要な数式を書くだけで計算をさせたいからです。設計・研究のために計算している最中にプログラムやデバッグをさせることは、設計・研究の対象への集中を削ぐことになるからです。ワンライナー式はエディタでのコピー・修正・比較が楽だからです。
もちろん無理やりにワンライナーで記述することは避けるべきです。ワンライナーで計算させるメリットがないだけの複雑さの計算を行うときは、躊躇することなく後に述べるファイル実行に切り替えてください。
ワンライナー実行の具体例
次のように計算させたい Python sf 式を引用符で囲んで、その前に 「python -u sfPP.py」を挿入した文字列をコマンドラインで実行させます。
以下の Python sf 式では、決まりきった「python sfPP "....."」 や 「sfPP.py "...."」を省略して、引用符の内側 .... の部分だけを書いていきます。下のように左上に「sf expression」と書いてあるワンライナーの Python sf 式は、この意味に解釈ください。
3+4 =============================== Z7
コマンド実行本稿では、Python sf ワンライナーを「微細構造定数;;`eQ^2/(h`` c` 4 `π ε0`)」のように書いていきます。これは「;;」以降の文字列を取り出して引用符で囲み、「python sfPP.py " Q^2/(h`` c` 4 `π ε0`)"」とコマンド・ラインで実行させることを意味しています。コメント部分「微細構造定数;;」なしの Python sf 式だけでも使います。私自身は、そのような WZ エディタのマクロを組んで、ctrl + O + C 操作で、引用符の追加など、何時も行う文字列処理をエディタ・マクロで実行させています。できましたら、お使いのエディタのコンソール・モードにそのようなマクロを組み込んで Python sf を使ってください。
エディタのコンソール・モードを使わずに、取り急ぎコードをテスト実行させたいときにはPython sf 式、すなわち「;;」以降の文字列を " ... " と引用符で囲み、その前に「python sfPP.py 」文字列を追加した文字列をエディタで作り、dos のコマンド・ラインに copy and paste し直して実行させてください。クリップ・ボードにあるコピーされた文字列は、dos 画面で「alt + space → e → p 」操作だけで dos 画面に貼り付けられます。
vim script
上で述べた python sf 式の文字列からをワンライナー実行させる vim scriptを作ってこちらに公開してあります。Vimmer の方はこちらを御試しください。
kidlelib
上で述べた python sf 式の文字列からをワンライナー実行させる python プログラムを作ってあります。Python の作者 Guido が作った idle library を修正を加えて、コンソール画面を追加したものを作りました。pythonSf095?.zip の中に kidlelib ディレクトリ以下に python source があります。これを実行させる kidle.py は mtCm カレント・ディレクトリにあります。mtCm カレント・ディレクトリの DOS 窓から下の様に立ち上げます。
start python kidle.py
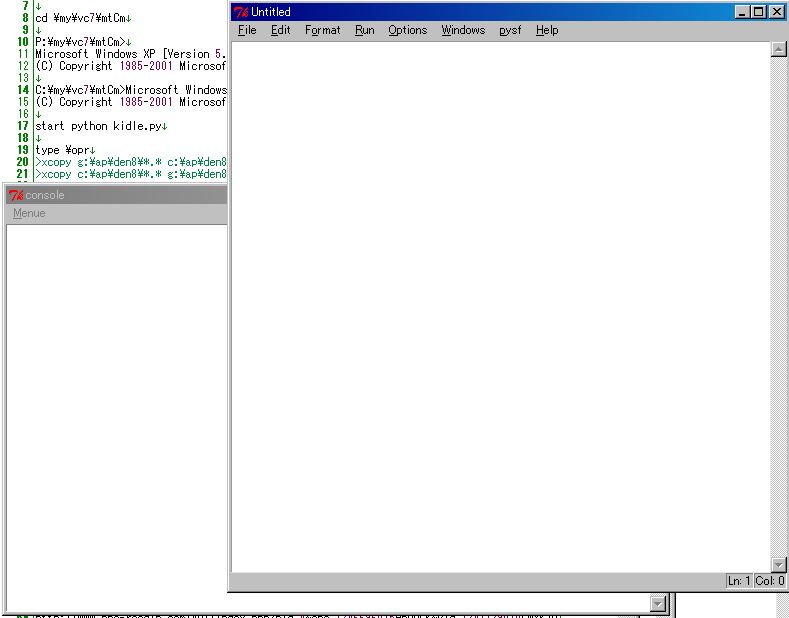
ここで「Untitled エディタ画面」画面上にメモを書いていきます。Python sf 式を書いた行にカーソルを置いておき、「alt + p -->C」操作をすると、そのカーソル行にある文字列を python sf 式とみなして「python -u sfPP.py "..."」で囲み「コンソール・ウィンドウ」側に貼り付けて実行させます。
その実行結果は次のようになります。
■ Python sf による簡潔な計算
Python sf プリプロセッサを介すことで、計算式を簡便に・日常使っててるメモ書きの数式と殆ど同じ形式で書けます。
- 数学での積:*演算子の省力を可能にします
- 数学で多用されるギリシャ文字を使えるようにします。
- 記号∇□∂△を使えるようにします。
- 「`」文字を変数名の前後に追加できるようにして、名前文字列に使える範囲を拡張します。
- Python の lambda 構文で λ 文字を使えるようにします
- 「~」を演算子記号の前に追加できるようにして、演算子を拡張します
- =:, := によりファイル変数の読み書きを行います
Python はプログラム一般を記述するための言語です。そのため Python で記述した計算式は冗長になってしまいます。
例えば 12Hz 複素振動の時刻 0.1sec における複素振幅は、下の Python code を使って計算できます。
//@@ import numpy as sc t = 0.1 # second f= 12 # Hz print sc.exp(1j* 2 * sc.pi * f * t) //@@@ (0.309016994375+0.951056516295j)
この python コードは次の点で冗長です。
- exp(..) 関数のように基本的な関数は「import numpy as sc」のようなモジュール取り込み文無しで使えることが望ましい。基本数値関数は初めから組み込まれているべき。
- pi のような計算で頻繁に出てくる定数も、「import numpy as sc」のようなモジュール取り込み文無しで使えることが望ましい。組み込み定数とすべき。
- 「# second, # Hz」のコメント文を一々書くのも面倒だが、これを省くと、コードのドキュメント性が悪くなってしまう。コメントの無いコードだけからでは、何を計算させているのかが極端に読み取りにくくなる。単位系も計算ソフトに組み込まれていれば、コード自体でコメントを付けたときと同程度のドキュメント製を持たせられる。
- 日常での数式の書き方のように、積の * 演算子は省略可能にしたい。
- 虚数記号 1j は、できることなら数学で使う i を使いたい。
- 人間に計算結果を知らせるには print 文は必須だ。でも逆に省けないのならば、必ず print 文が存在する。ならばデフォルトで print 文が存在するように計算機側が振舞うべき。
Python code には、上のような冗長性があるとしても、Python で記述する限りは、上の改善すべき問題に対処する方法はありません。
Python sf ならば、これらの冗長さを回避した次のような簡潔なワンライナーの計算式で同じことを行わせられます。
t,f=0.1,12; exp(`i 2 pi f t) =============================== (0.309016994375+0.951056516295j)
また上の式では 積の * 演算子を省略しています。sc.pi での sc 名前空間ではなく、グローバル名前空間に pi 定数を置いています。複素数を 1j ではなく `i で表記させています。
---- 多重代入 ----Python では 「t,f = 0,1, 12」のように一つの代入文で複数の値を設定できます。関数の戻り値でも、複数の値を返せます。この二つを組み合わせて 「t,f=functionRetuningPairVal(..)」のような書き方も可能です。この機能は結構便利です。多重ループを一つの for 文で書けるよう拡張できたりします。
`pi の代わりにギリシャ文字の `π を使って、日常的に書いている数式に より近づけられます。
t,f=0.1,12; exp(2 `π `i f t) =============================== (0.309016994375+0.951056516295j)
計算ソフトではギリシャ文字を使うことで、ドキュメント性を大幅に高められます。漢字文化圏の者は、ギリシャ文字のフォントが簡単に読み書きできるのですから、それを活用しない手はないでしょう。アルファベット文字だけで閉じているヨーロッパ文化圏の者には、この発想は無理なようです。ギリシャ文字の他に日常の計算で使うことの多い「∇□∂△」記号も扱えるようにしています。
Python sf では、単位系付きでの計算が可能です。次のような具合です。
t,f=0.1s`,12Hz`;exp(`i 2 pi f t) =============================== (0.309016994375+0.951056516295j)
Python sf では ts() を呼び出すと sympy package を使えるようになり、シンボリックな処理が可能ななります。単位系付き演算もシンボリックな単位付になります。
ts(); C,R=4.7uF`,1k` Ω`; R C =============================== 0.0047*s`
一方で exp(..) の引き数が物理次元を持つとき、その単位が打ち消しあっていなければなりません。物理単位が残ったままの値は計算できません。下のような単位が打ち消しあった計算でないと物理的な意味を持ちません。
ts(); C,R,t=1.0uF`,1k` Ω`, 1.3ms`; exp(`i 2 pi t/(R C) ) =============================== (-0.309016994375+0.951056516295j)
シンボリックな単位付で計算してやると、誤って物理的に無意味な計算をしてしまうことを防げます。下のような具合です。
ts(); C,R=1uF`,1k` Ω`; exp(`i 2 pi/(R C) ) Symbolic value, can't compute at excecuting:exp(k__bq_i___ * 2 * pi/(R * C) )
---- λ:lambda 式 ----Python は lambda 式を書けます。関数プログラミングに慣れた方でないと、最初は面食らうのですが、慣れると便利です。Python sf は、この lambda 式をギリシャ文字 λ で表現できます。下のような具合です。
(lambda x:-x^2)(3) =============================== -9 (λ x:-x^2)(3) =============================== -9これだけでは λ式の効用がよく分らない方も思います。「exp(-x^2) の [-3,3] 範囲のグラフを下のように書けます」といったら、少しは λ 式の有用性を分ってもらえると思います。
plotGr(λ x:exp(-x^2), -3,3)
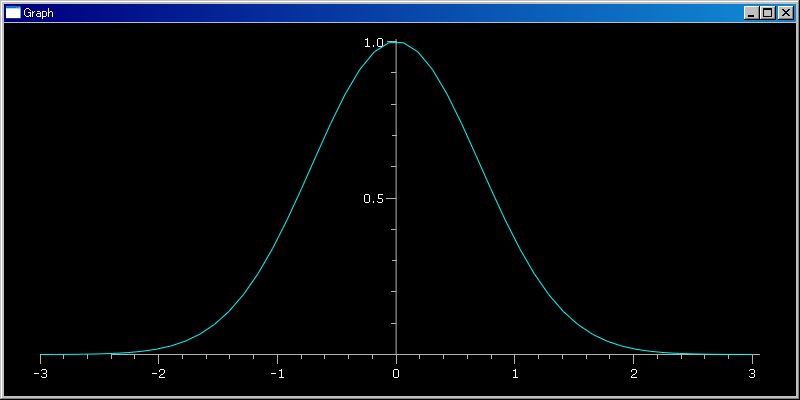
下の三つの式は同じ意味であり同じ動作になります。でも上のように書いたほうが簡潔であり python 式の意味が分りやすくなります。
plotGr(lambda x:exp(-x^2), -3,3) f = labmda x: exp(-x^2); plotGr(f, -3,3) def f(x):return exp(-x^2); plotGr(f, -3,3)漢字の λ はアルファベットの lambda より目立つので、λ 式を使っていること、λ式の範囲が強く表現されます。漢字の効用です。実は三角関数や exp といった基本数値関数は加減乗除べき乗算と関数合成が可能な Python sf 関数として実装しています。さらに恒等関数 `X も Python sf 関数です。ですから exp(x^2) 関数のグラフを描かせるには、下の Python sf 式で済ませられます。
plotGr(exp(-`X^2),-3,3)でも、特殊関数など Python sf 基本数値関数以外の関数の組み合わせが必要になったときはλ式が活躍します。コンピュータ・サイエンスの教科書で λ 式の例題として頻出するチャーチ数の計算が Python sf で、実際に下のように計算できるのを見てもらったら、lambda を λ で書けることの凄まじいまでの有利さを分ってもらえると思います。如何でしょうか?
Z='1';S =λ s:s+'1';(λ s:λ z:s(s(z)))(S)(Z) =============================== 111 Z='1';S =λ s:s+'1';(λ s:λ z:s(s( s(s(s(z))) )))(S)(Z) =============================== 111111Python sf は Python 言語で蓄積されている多分野のライブラリを簡潔なワンライナーで利用できることにも目を向けてください。Python sf の利用は数値・数式計算だけに限定されません。
バック・クォート:` 記号による変数・関数名の拡張
たぶん大部分の方は「 s`, `π や `i などと変数名の前についている逆クォート:` 記号は何なんだ」と思われると思います。これが Python sf の一番自慢できる特徴です。Python に限ると使える変数・関数名はアンダースコアとアルファーニューメリックで記述されるものに限定されます。この範囲だけで計算ソフトに必要な変数・関数名をも まかなおうとすると、既存の python 変数・関数名とぶつかります。変数の前後に「`」記号をつけたものも変数名として許すことで、Python の変数名と計算ソフトに必要な変数名を矛盾無く共存させられます。単純なことですが、計算式を Python 文法と矛盾することなく簡潔にドキュメント性高く記述するのに、非常に効果があります。
例えば SI 単位系では秒の単位は s で表現することに決まっています。でもプログラム・コードには、そんな決まりごとを持ち込めません。理工学分野での 12s と書かれた数値は 12 秒を意味することが多いでしょう。12m/s とかかれたら、速度を意味していることが大部分でしょう。 でもプログラミング言語では s は秒の意味を表すとの共通認識はありません。ステップ数を意味しているかもしれません。表面積の意味かもしれません。ですから SI 単位系で秒が s だと決まっていても、秒の単位に s を割り振れません。でも「`」を後ろ側に追加した s` を秒に割り振るのならば、Python program での変数名と秒の単位の s` が矛盾することなく、計算式の物理的な意味を明確にしながら、簡潔に記述できます。Python sf では変数名の後ろ側に「`」を追加したものに単位系と物理定数の名前を割り当てています。
逆に名前の前側に「`」を追加した名前は、物理単位が意味を持たない定数・関数に割り当てています。上の例で使った単位虚数 `i, 円周率 `pi,`π、以外に BOOL体変数 `1,`0, BOOL 体多項式`Z、Pauli 行列 `σx,`σy,`σz, 三次元 Levi Civita テンソル `εL などをデフォルトで定義しています。以下のような計算ができます。
# BOOL field calculation
`1+`1 =============================== 0 `1+`0 =============================== 1 `1*`1 =============================== 1 (`Z+`1)^3 =============================== `Z^3+`Z^2+`Z+1 (`Z+`1)^5 =============================== `Z^5+`Z^4+`Z+1 (`Z+`1)^3 + (`Z+`1)^5 =============================== `Z^5+`Z^4+`Z^3+`Z^2 (`Z^5+1)/(`Z+1) =============================== (Pl(`Z^4+`Z^3+`Z^2+`Z+1), Pl(0))
# Pauli matrix calculation `σx =============================== [[ 0. 1.] [ 1. 0.]] ---- ClTensor ---- `σy =============================== [[ 0.+0.j 0.-1.j] [ 0.+1.j 0.+0.j]] ---- ClTensor ---- `σx `σx - `σy `σx =============================== [[ 1.+1.j 0.+0.j] [ 0.+0.j 1.-1.j]] ---- ClTensor ---- 1/(`σx `σx - `σy `σx) # inverse by 1/... =============================== [[ 0.5-0.5j 0.0+0.j ] [ 0.0+0.j 0.5+0.5j]] ---- ClTensor ---- `σz/(`σx `σx - `σy `σx) =============================== [[ 0.5-0.5j 0.0+0.j ] [ 0.0+0.j -0.5-0.5j]] ---- ClTensor ---- `σz (`σx `σx - `σy `σx)^-1 =============================== [[ 0.5-0.5j 0.0+0.j ] [ 0.0+0.j -0.5-0.5j]] ---- ClTensor ---- # Matrix * vector `σx [2,3] =============================== [ 3. 2.] ---- ClTensor ---- # vector * Matrix [2,3] `σx =============================== [ 3. 2.] ---- ClTensor ----
# Levi Civita tensor calculation `εL =============================== [[[ 0. 0. 0.] [ 0. 0. 1.] [ 0. -1. 0.]] [[ 0. 0. -1.] [ 0. 0. 0.] [ 1. 0. 0.]] [[ 0. 1. 0.] [-1. 0. 0.] [ 0. 0. 0.]]] ---- ClTensor ---- # Tensor * vector `εL [1,2,3] =============================== [[ 0. 3. -2.] [-3. 0. 1.] [ 2. -1. 0.]] ---- ClTensor ---- # vector * Tensor * vector a,b=[1,2,3],[4,5,6];a `εL b =============================== [ 3. -6. 3.] ---- ClTensor ---- # ちなみに、上の計算はベクトル外積にマイナス符号を付けたものになります。 a,b=[1,2,3],[4,5,6]; sc.cross(a,b) =============================== [-3 6 -3]
チルダ:~ 記号による演算子の拡張
Python sf は「~」記号を使って演算子を可能に拡張します。行列を ~[...] で表記できるのが特に便利です。Python のリスト内包表記の最初に、チルダ記号:~ を追加するだけでベクトルや行列を生成できるのも便利です。
#vector ~[1,2,3] =============================== [ 1. 2. 3.] ---- ClTensor ---- # vector * scalar ~[1,2,3] * 3 =============================== [ 3. 6. 9.] ---- ClTensor ---- # vector * vector:内積:inner product
~[1,2,3] ~[4,5,6] =============================== 32.0 a,b=~[1,2,3], ~[4,5,6]; a b =============================== 32.0 # matrix ~[[1,2],[3,4]] =============================== [[ 1. 2.] [ 3. 4.]] ---- ClTensor ---- # matrix * vector vc, mt = ~[1,2], ~[[1,2],[3,4]]; mt vc =============================== [ 5. 11.] ---- ClTensor ---- # vector generated by an enclosure
~[2k for k in range(5)] =============================== [ 0. 2. 4. 6. 8.] ---- ClTensor ---- # matrix generated by an enclosure
~[[2k for k in range(5)], [2k+1 for k in range(5)]] =============================== [[ 0. 2. 4. 6. 8.] [ 1. 3. 5. 7. 9.]] ---- ClTensor ---- ~[(2k,2k+1) for k in range(5)] =============================== [[ 0. 1.] [ 2. 3.] [ 4. 5.] [ 6. 7.] [ 8. 9.]] ---- ClTensor ----
range(5) =============================== [0, 1, 2, 3, 4]
---- introspection_1:help ---- についてPython には、introspection 機能:ドキュメントを覗き込む機能が備わっています。help(..) 関数の引数に関数名またはモジュール名を与えてやれば、その関数やモジュールに書かれている説明コメント文字列を取り出せます。下のような具合です。
help(range) range(...) range([start,] stop[, step]) -> list of integers Return a list containing an arithmetic progression of integers. range(i, j) returns [i, i+1, i+2, ..., j-1]; start (!) defaults to 0. When step is given, it specifies the increment (or decrement). For example, range(4) returns [0, 1, 2, 3]. The end point is omitted! These are exactly the valid indices for a list of 4 elements. =============================== None以下、訳の分らん関数やモジュールが出てきたときは help(..) とやってみてください。そしてご自分の手で Python sf 式を range(..) などの動作を確認するコードを書いて実行してみてください。その関数の動作を よく理解できるはずです。Python sf ならば、式を書くだけで その式の値をコンソールに打ち出します。print 命令さえ書かずに済ませられます。下のような具合に range(..) 関数を動作させてみれば、上の分りにくい英語の文章を完全に理解できると思います。
range(3,10,2) =============================== [3, 5, 7, 9]大部分の Python sf 式は一行です。テストの手間など たかが知れています
Python sf の基本数値関数
先に Python sf では、exp 関数がデフォルトで組み込まれており、exp 関数を実装してある numpy モジュールの import なしで使えることを示しました。その他のデフォルト組み込み関数には absF, sin, cos, tan, sinh, cosh, tanh, arcsin, arccos, arctan, log, log10, sqrt があります。これらは全て複素引数値でも計算できます。
cos(pi/3) =============================== 0.5 cos(pi+`i) =============================== (-1.54308063482-1.43920638015e-16j) log(-1) =============================== 3.14159265359j log(-1+`i) =============================== (0.34657359028+2.35619449019j) arcsin(1) =============================== 1.57079632679
ベクトル値を引数にとる ファースト・フーリエ変換 fft, 逆変換 ifft 数値関数も用意してあります。頻繁に使うからです。引数のベクトル長は任意のものを与えられます。 2 のべき乗に限りません。
fft([1,2,3,4,5]) =============================== [ 6.70820393+0.j -1.11803399+1.53884177j -1.11803399+0.36327126j -1.11803399-0.36327126j -1.11803399-1.53884177j] ---- ClTensor ---- ifft( fft([1,2,3,4,5]) ) =============================== [ 1.+0.j 2.+0.j 3.+0.j 4.+0.j 5.+0.j] ---- ClTensor ----
正方行列を引数値にとる expm, logm も基本数値関数に加えてあります。
expm(~[[1,2,],[3,4]]) =============================== [[ 51.9689562 74.73656457] [ 112.10484685 164.07380305]] ---- ClTensor ---- expm(`σx) =============================== [[ 1.54308063 1.17520119] [ 1.17520119 1.54308063]] ---- ClTensor ---- t=2.7; expm(`i t `σx) =============================== [[-0.90407214+0.j 0.00000000+0.42737988j] [ 0.00000000+0.42737988j -0.90407214+0.j ]] ---- ClTensor ----
tuple,list, array, ClTensor
Python には、tuple,list というシーケンス・データを扱うコンテナが予約語として備わっています。numpy モジュールには array(..) 行列・ベクタが備わっています。Python sf は numpy を継承した ClTensor を新たに設けて、行列・ベクタを扱いやすくしています。新たに Python sf を使うとき、これらの違いの理解が最初の関門です。厳密に文法から説明していると何十ページも必要です。でも、最初のうちは「習うより慣れろ」で行けてしまいます。
でも、以下の大きな特徴・違いは理解しておくべきです。
tuple は変更できないシーケンス・データです。丸括弧で囲んで表現します。
tpl=(1,2,3)
===============================
(1, 2, 3)
tpl=(1,2,3); tpl[1]=10;tpl
'tuple' object does not support item assignment at excecuting:tpl[1]=10
tpl=(100,)+(1,2,3); tpl # add tuples
===============================
(100, 1, 2, 3)
tpl=(1,2,3)*3;tpl # multiply with integer
===============================
(1, 2, 3, 1, 2, 3, 1, 2, 3)
help(tuple)
class tuple(object)
| tuple() -> an empty tuple
| tuple(sequence) -> tuple initialized from sequence's items
・
・
| index(...)
| T.index(value, [start, [stop]]) -> integer -- return first index of value.
| Raises ValueError if the value is not present.
list は変更できるシーケンス・データです。角括弧で囲んで表現します。
lst=[1,2,3] =============================== [1, 2, 3] lst=[1,2,3]; lst[1]='a'; lst # list is mutable =============================== [1, 'a', 3] lst=[1,2,3]; lst.append(100);lst =============================== [1, 2, 3, 100] [100]+[1,2,3], [1,2,3]*2 # add, multiply =============================== ([100, 1, 2, 3], [1, 2, 3, 1, 2, 3])上の最後の式で「[100]+[1,2,3], [1,2,3]*2」のように二つの式を「,」で区切って並べると、Python では tuple になります。
a= [100]+[1,2,3], [1,2,3]*2; type(a) =============================== <type 'tuple'>
numpy の sc.array(..) により行列やベクトルを作れます。sc.array(..) の引数に tuple または list データを与えると numpy の行列やベクトルが帰ってきます。クラス・インスタンスを要素とする行列・ベクタも作れますが、最初のうちは数値のみの行列・ベクタにしておきましょう。
vct=sc.array([1,2,3]);vct # integer vector =============================== [1 2 3] vct=sc.array([1.0, 2,3]);vct # float vector =============================== [ 1. 2. 3.] vct=sc.array([1.0, 2,3]);vct*3 # vector * integer =============================== [ 3. 6. 9.] vct=sc.array([1,2,3])+100 # vector + integer =============================== [101 102 103] vct1,vct2=sc.array([1,2,3]),sc.array([4,5,6]); vct1+vct2 # vector+ vector =============================== [5 7 9] vct1,vct2=sc.array([1,2,3]),sc.array([4,5,6]); vct1*vct2 # vector* vector =============================== [ 4 10 18] mt=sc.array([[1,2],[3,4]]);mt # int matrix =============================== [[1 2] [3 4]] mt=sc.array([[1,2],[3,4]]);mt [10,100] # matrix * lst =============================== [[ 10 200] [ 30 400]] mt=sc.array([[1,2],[3,4]]);mt mt # matrix * matrix =============================== [[ 1 4] [ 9 16]]
ベクタや行列の積は、要素ごとの積演算したものになります。数学でのベクタや行列の積を計算させるときには numpy の sc.dot(..) 関数を使います。
vct1,vct2=sc.array([1,2,3]),sc.array([4,5,6]); sc.dot(vct1,vct2) # inner product =============================== 32 mt=sc.array([[1,2],[3,4]]);sc.dot(mt, [10,100]) # matrix * lst =============================== [210 430] mt=sc.array([[1,2],[3,4]]);sc.dot(mt, mt) # matrix * matrix =============================== [[ 7 10] [15 22]]
~[..] により ClTensor 行列やベクトルを作れます。
vct=~[1,2,3];vct # default float vector =============================== [ 1. 2. 3.] ---- ClTensor ---- vct=~[1,2,3,int];vct # integer vector =============================== [1 2 3] ---- ClTensor ---- vct=~[1, 2,3];vct*3 # vector * integer =============================== [ 3. 6. 9.] ---- ClTensor ---- vct=~[1,2,3]+100 # vector + integer =============================== [ 101. 102. 103.] ---- ClTensor ---- vct1,vct2=~[1,2,3],~[4,5,6]; vct1+vct2 # vector+ vector =============================== [ 5. 7. 9.] ---- ClTensor ---- vct1,vct2=~[1,2,3],~[4,5,6]; vct1*vct2 # vector* vector =============================== 32.0 mt=~[[1,2],[3,4]];mt # default float matrix =============================== [[ 1. 2.] [ 3. 4.]] ---- ClTensor ---- mt=~[[1,2],[3,4], int];mt # int matrix =============================== [[1 2] [3 4]] ---- ClTensor ---- mt=~[[1,2],[3,4]];mt [10,100] # matrix * lst =============================== [ 210. 430.] ---- ClTensor ---- mt=~[[1,2],[3,4]];mt mt # matrix * matrix =============================== [[ 7. 10.] [ 15. 22.]] ---- ClTensor ---- mt=~[[1,2],[3,4]];1/mt # inverse matrix by divide =============================== [[-2. 1. ] [ 1.5 -0.5]] ---- ClTensor ---- mt=~[[1,2],[3,4]];mt^-1 # inverse matrix by power =============================== [[-2. 1. ] [ 1.5 -0.5]] ---- ClTensor ---- mt=~[[1,2],[3,4]];mt^-1 [100,200] # inverse matrix * list =============================== [ 2.84217094e-14 5.00000000e+01] ---- ClTensor ----
ClTensor 行列・ベクトルはデフォルトで float 要素にします。numpy でのように integer ではありません。Integer 行列の要素に float 値を代入したとき、小数点以下が切り捨てられてしまう問題があるからです。
vct=sc.array([1,2,3]);vct[1]=7.777; vct =============================== [1 7 3] vct=~[1,2,3];vct[1]=7.777; vct =============================== [ 1. 7.777 3. ] ---- ClTensor ----
ClTensor の行列・ベクトルの積演算結果は、数学での積演算と同じです。通常は numpy ではなく ClTensor の行列・ベクトルを使っておいたほうが、日常の数式表記に似せられます。
Python sf での繰り返し構文とイタレータ
python のループ構文は「for 要素 in イタレータ」の次にインデントされた式、または文を続けることで記述されます。
for index in iteraor:
index を含んだ式 or 文
index を含んだ式 or 文
・
・
index を含んだ式 or 文
Python loop syntax exmaple
//@@
for k in range(5):
m = 2 * k
print m**2
//@@@
0
4
16
36
64
イタレータ部分には、リスト、ジェネレータ関数、行列など、多くの Python で複数のデータを扱う要素を持ってこれます。 ユーザーが作ったジェネレータ関数を このイタレータ部分に持ってくれば、ループの働き方を広い範囲で指定できます。 このことを活用すれば、ワンライナーであっても可読性を保ったまま、ループ構文を扱えます。ワンライナーで、二次元、三次元分布データを計算させ、表示させることまで可能になります。
ワンライナーは簡潔にかけることに意味があります。ワンライナーに if 文を詰め込むべきでは有りません。可読性が損なわれます。ループで実行する文や式が一つだけならば、可読性も損なわれません。そのようなループ構文ならば Python sf ワンライナーでも扱えます。上の for loop python cods と同じことを Python sf ワンライナーで次のように記述できます
for k in range(5):print (2k)^2 0 4 16 36 64 ------------------------------- None
計算ソフトでは等差数列を必要とすることが多く有ります。でも range(..) 関数では整数しか作れません。sc.arange(..) でも複素数を含んだ数列は無理です。なので、Python sf では arsq(..) 関数を用意しています。
help(arsq)
等差数列タプルを start, size, stride 引数で生成して返す
return arithmetic sequence generated with argument start, size, stride
e.g.
N=10;arsq(1,N, 3)
===============================
(1, 4, 7, 10, 13, 16, 19, 22, 25, 28)
N=5; arsq(1+`i,N, (2+4`i)/N)
===============================
((1+1j), (1.3999999999999999+1.8j), (1.8+2.6000000000000001j),
(2.2000000000000002+3.4000000000000004j), (2.6000000000000001+4.2000000000000002j))
arsq は便利です。log 関数の [1, 1+5i] 区間の変化の様子は次の Python sf ワンライナーで表示させられます。
N=50;lst=arsq(1,N,(1+5`i)/N);plotGr([log(x).real for x in lst]);plotGr([log(x).imag for x in lst],color=orange)
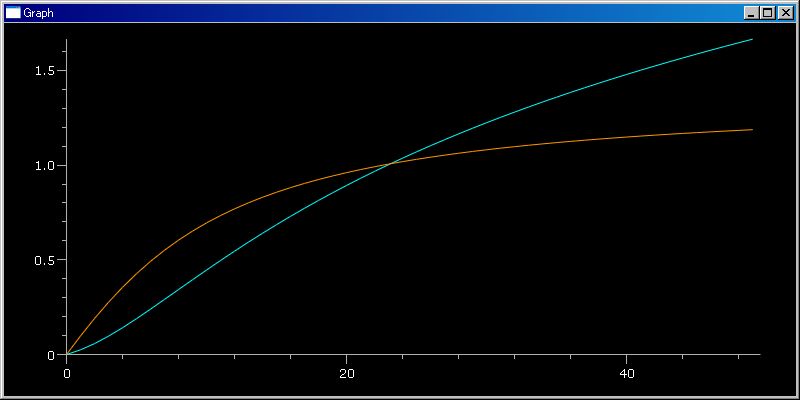
等差数列ではなく、範囲を N 等分してできるシーケンス・データが欲しいいときもあります。そのために klsp(..) 関数を用意しています。厳密には klsp(..) は (N-1) 等分して両端を含んだリストを返します。arsq(は右端を返しません。
N=6;arsq(-1,N,2/N) =============================== (-1.0, -0.66666666666666674, -0.33333333333333337, 0.0, 0.33333333333333326) N=6;klsp(-1,1,N) =============================== [-1. -0.6 -0.2 0.2 0.6 1. ] ---- ClTensor ----
klsp(..) は分割数を偶数にしておけば、領域の中心を跨いだ数列を返します。位置 0 などで発散する関数を検討するとき便利です。次のように [-2,2] の範囲での log 関数を 0 での発散を避けながらグラフ表示させられます。
klsp(..) は分割数の引数を指定しないときは、デフォルトの 50 になります。大多数のグラフ表示には都合のよい分割数です。
len(klsp(-1,1)) =============================== 50 lst=klsp(-2,2);plotGr([log(x).real for x in lst]);plotGr([log(x).imag for x in lst],color=orange)
計算ソフトでは多重ループの計算が頻出します。これも多重ループ専用のイタレータ mrng,masq,mitr を用意することで Python sf ワンライナーで記述できるようなります。
list(mrng(3,4)) =============================== [(0, 0), (0, 1), (0, 2), (0, 3), (1, 0), (1, 1), (1, 2), (1, 3), (2, 0), (2, 1), (2, 2), (2, 3)] list(mrng([1,4],[2,6])) =============================== [(1, 2), (1, 3), (1, 4), (1, 5), (2, 2), (2, 3), (2, 4), (2, 5), (3, 2), (3, 3), (3, 4), (3, 5)] list(mrng([1,6,2],[2,6])) =============================== [(1, 2), (1, 3), (1, 4), (1, 5), (3, 2), (3, 3), (3, 4), (3, 5), (5, 2), (5, 3), (5, 4), (5, 5)]mrng(..) を使えば、二変数を引数とする sin( (x+y)/||(x,y)||) の三次元グラフを下のようにワンライナーで書けます。
N,dct=50,{};for x,y in mrng(N,N):dct[x,y]=sin(((x-(N+1)/2)+(y-(N+1)/2))/sqrt((x-(N+1)/2)^2+(y-(N+1)/2)^2));renderMtrx(dct)
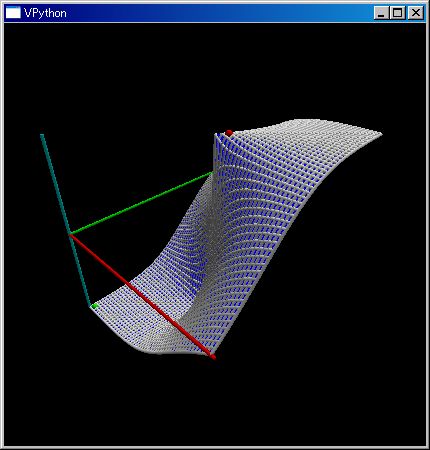
---- 辞書:dict ---- についてPython にはキーと値の組で表される辞書:dict コンテナも用意されています。{key:value, ...} で表現します。dict[key] で値を取り出せます。次のような具合です。
dct = {0:'a', 1:'b'};dct =============================== {0: 'a', 1: 'b'} dct = {0:'a', 1:'b'};dct[1] =============================== b辞書のキーに整数 tuple を指定すると、辞書要素を整数インデックスで取り出せます。行列に似ています。
dct = {(0.0):1, (0,1):2, (1,0):3, (1,1):4};dct =============================== {0.0: 1, (0, 1): 2, (1, 0): 3, (1, 1): 4} dct = {(0.0):1, (0,1):2, (1,0):3, (1,1):4};dct[1,1] =============================== 4renderMtrx(..) 三次元グラフ表示関数は、dict で表される行列データも受け付けるように作ってあります。それを今回利用しました。
---- sc.source によるソース・コード表示 ---- についてsc.source(...) により、関数やグラフの Python ソース・コードを取り出せます。Python sf では、大部分のソース・コードを公開しており、参照・修正可能です。例えば、mrng(..) のソース・コードは次のようになっています。
sc.source(mrng) In file: D:\my\vc7\mtCm\pysf\basicFnctns.py def mrng(*args): """' multiple range generator list(mrng(2,3))" =============================== [(0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2)] list(mrng((1,4),(5,7))) =============================== [(1, 5), (1, 6), (2, 5), (2, 6), (3, 5), (3, 6)] list(mrng((1,6,2),(5,9,3))) =============================== [(1, 5), (1, 8), (3, 5), (3, 8), (5, 5), (5, 8)] an example of usage dctAt={} for i,j in mrng(10,20): dctAt[i,j] = i+j '""" head, tail = args[0], args[1:] if type(head) in [int, long, float]: head = range(int(head)) elif isinstance(head, tuple) or isinstance(head, list): head = range(*head) if tail: for i in head: for j in mrng(*tail): if isinstance(j, tuple): yield (i,)+j else: yield (i, j) else: for i in head: yield i =============================== None高々 15 行の Python コードですが、再帰プログラムになっており、任意の多重ループを扱えるようになっています。Python コードを読める方ならば、下手な説明文より、この Python コードの方が分りやすいと思います。help(..) での説明では理解できないときは sc.source(...) も試してください。
Python では *args 引数を使うことで、任意個数の引数を扱えます。mrng(..) 関数のコードは、もう殆ど関数プログラミングのコードになっています。このような書き方ができることをメーリング・リストで教えてもらい、それから Python 言語のファンになりました。Python を本格的に勉強するか迷っている方は、上のコードをデバッガ pdb で追ってみてください。Python 習得に時間を割く価値があることを分ってもらえと思います。多くのハッカーが Python を好む理由を共感してもらえると思います。
Python sf では、このようなコードをユーザー側で自由に開発・追加できます。十数行のコードで素晴らしい機能を追加できること分ってもらえますでしょうか。
masq(..)/mitr(..) は mrng の考え方を等差数列/イタレータに適用したものです。次のコード例を見てもらえば、その働きがわかると思います。これでは分り難いときは、是非とも 自分で具体例を作って試してください。直ぐに分ると思います。
N=4;list(masq([-1,N,2/N], [0,N,1/N])) =============================== [(-1.0, 0.0), (-1.0, 0.25), (-1.0, 0.5), (-1.0, 0.75), (-0.5, 0.0), (-0.5, 0.25), (-0.5, 0.5), (-0.5, 0.75), (0.0, 0.0), (0.0, 0.25), (0.0, 0.5), (0.0, 0.75), (0.5, 0.0), (0.5, 0.25), (0.5, 0.5), (0.5, 0.75)] list( mitr(range(3),arange(0,1,1/3)) ) =============================== [(0, 0.0), (0, 0.33333333333333331), (0, 0.66666666666666663), (1, 0.0), (1, 0.33333333333333331), (1, 0.66666666666666663), (2, 0.0), (2, 0.33333333333333331), (2, 0.66666666666666663)]
enmasq(..),enmitr(..) は masq(..), mitr(..) が数値を返すのに、そのインデックスも付け加えるようにしたものです。
N=4;list(enmasq([-1,N,2/N], [0,N,1/N])) =============================== [((0, 0), (-1.0, 0.0)), ((0, 1), (-1.0, 0.25)), ((0, 2), (-1.0, 0.5)), ((0, 3), (-1.0, 0.75)), ((1, 0), (-0.5, 0.0)), ((1, 1), (-0.5, 0.25)), ((1, 2), (-0.5, 0.5)), ((1, 3), (-0.5, 0.75)), ((2, 0), (0.0, 0.0)), ((2, 1), (0.0, 0.25)), ((2, 2), (0.0, 0.5)), ((2, 3), (0.0, 0.75)), ((3, 0), (0.5, 0.0)), ((3, 1), (0.5, 0.25)), ((3, 2), (0.5, 0.5)), ((3, 3), (0.5, 0.75))] list( enmitr(range(3),arange(0,1,1/3)) ) =============================== [((0, 0), (0, 0.0)), ((0, 1), (0, 0.33333333333333331)), ((0, 2), (0, 0.66666666666666663)), ((1, 0), (1, 0.0)), ((1, 1), (1, 0.33333333333333331)), ((1, 2), (1, 0.66666666666666663)), ((2, 0), (2, 0.0)), ((2, 1), (2, 0.33333333333333331)), ((2, 2), (2, 0.66666666666666663))]
enmasq(..),enmitr(..) を使うと、インデックスを使えるので行列の扱いが容易になります。先の sin( (x+y)/||(x,y)||) のグラフは次のようにも書けます。こちらならば、複数行で記述したときに近いドキュメント性もあります。
N,dct=50,{};lst=klsp(-1,1,N);for idx,(x,y) in enmitr(lst,lst):dct[idx]=sin((x+y)/norm([x,y]));renderMtrx(dct)
なお arsq, mrng,arsq,mitr,klsp, enmasq, enmitr のソース・コードは公開されています。pysf\basicFnctns.py の中にあります。これらの機能に不満があるときは、改良版を御自分でコーディングしてください。Python sf プリプロセッサは任意の Python コードを対象とします。
2D,3D グラフ表示
Python には pylab モジュールという matlab によく似た、また膨大なグラフ表示ライブラリが既に存在します。また mayavi モジュールも高度な 3D グラフ表示を可能にします。
でも、これらのモジュールを使ってグラフを表示させるには十数行の Python コードを書かねばなりません。Python sf は、最小の手間でグラフ表示を行います。大部分の日常計算では描かせるグラフは自分だけが見るグラフです。そのグラフに凡例など必要ありません。必要最小限のパラメータ設定にすれば、ワンライナーでも関数のグラフを描けます。
最も よく使う 一変数引数の関数は plotGr(..) で表示させます。plotGr(..) は引数に「関数を与えること」/「シーケンス・データを与えること」どちらかの方法でグラフを表示させます。
plotGr(..) グラフ表示
一番普通に使うのが「plotGr(func, start=0, end=+1)」と関数と開始位置、終了位置のパラメータを与えるグラフ表示方法でしょう。
plotGr(sin,-3,5)
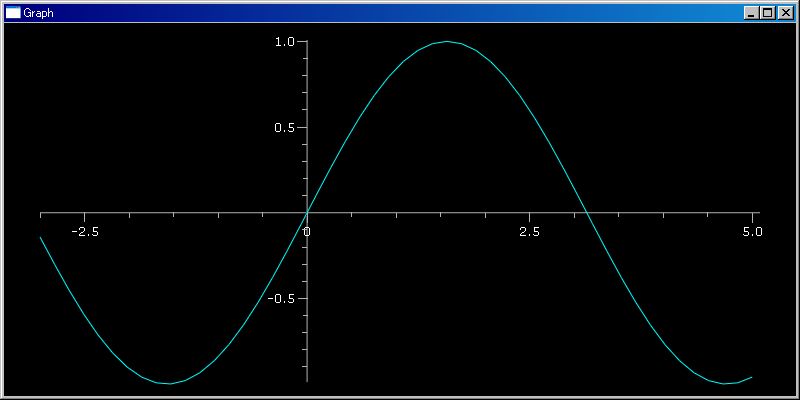
上のグラフではデフォルトの、表示領域の 50 点の値を直線で繋いで表示しています。グラフ表示のデータ点数を明示的に指定することもできます。下の例では [-3,5] の領域から 8 点の位置の関数値を計算し、それらを直線で繋いだグラフを表示しています。
plotGr(sin,-3, 5, 8)
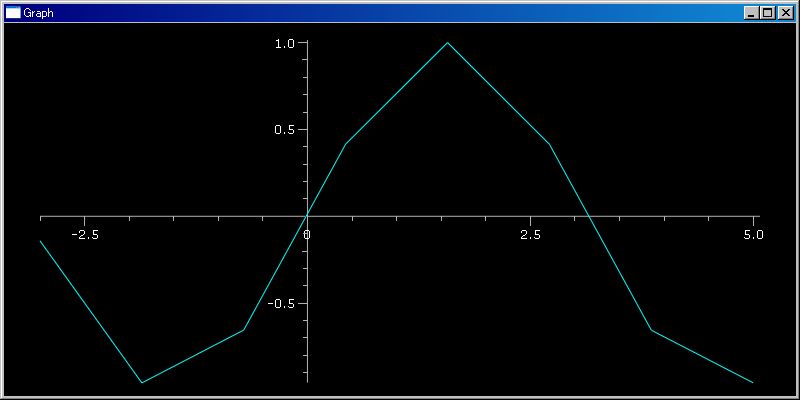
上のグラフ表示では、両端も含む 8 点のデータでグラフを描かせています。1/x のように無限大の点を含んでいても分割数が偶数だと、無限大の点を避けることが多いことを覚えておくと便利です。
plotGr(λ x:1/x,-1,1)
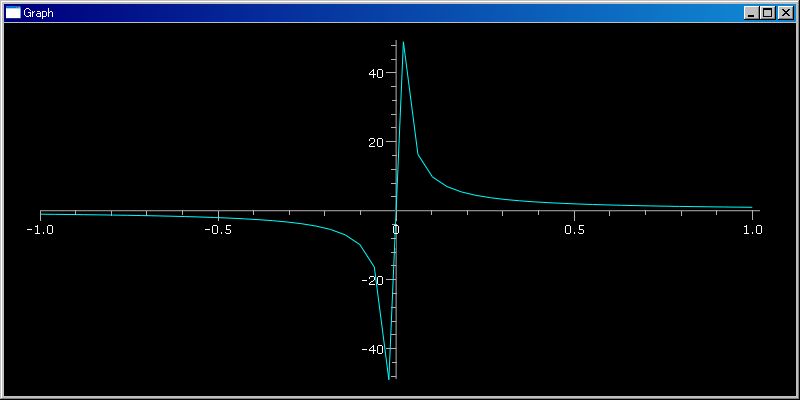
開始位置、終了位置のパラメータを与えないときは、デフォルトの表示範囲として 0 と 1 を使います
plotGr(sin)
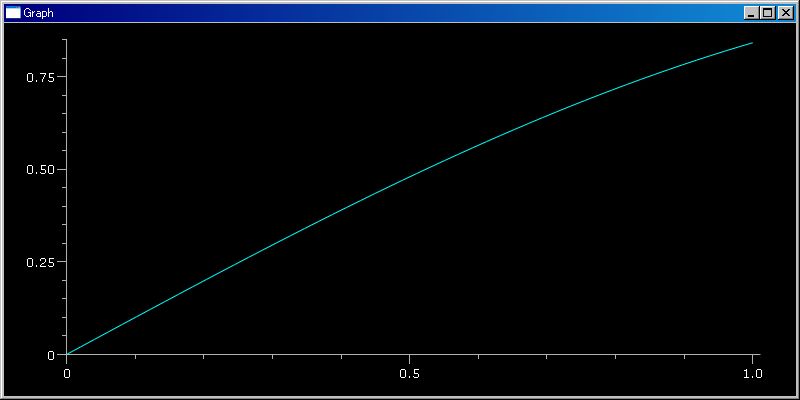
シーケンス・データを与えることでも、グラフを表示できます。このときの横軸値はシーケンス・データのインデックス整数値になります。
N=16;plotGr([sin(x) for x in arsq(-3,N,8/N)])
plotGr(..) を複数回実行すると、グラフを重ね書きします。color 引数を指定することでグラフの色を指定できます。
lst=klsp(0,2pi);plotGr(sin, lst); plotGr(cos,lst, color=orange)
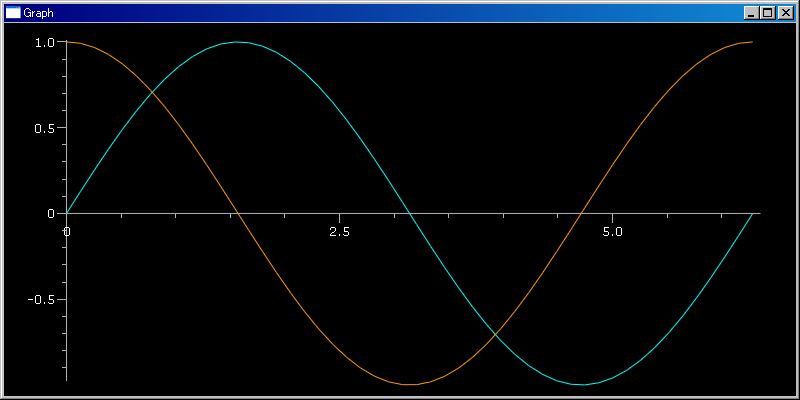
red = (1, 0, 0) black = (0, 0, 0) white = (1, 1, 1) red = (1, 0, 0) green = (0, 1, 0) blue = (0, 0, 1) yellow = (1, 1, 0) cyan = (0, 1, 1) magenta = (1, 0, 1) orange = (1, 0.6, 0) green = (0, 1, 0)
三次元グラフ表示 plot3dGr(..)
ニ変数関数の三次元グラフ表示をさせるのに plot3dGr(..) 関数が便利です。「plot3dGr(fun(x,y), x range, y range)」で「 [x range] x [y range] 」長方形定義域での関数 fun(x,y) 値の分布を表記します。
help(plot3dGr) plot3dGr(sin(norm(~[`X,`Y])), [-pi,pi])
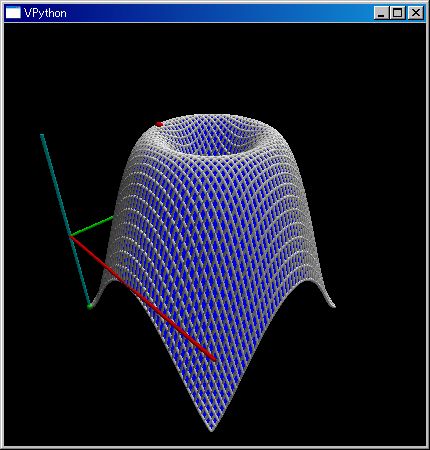
plot3dGr(cos(norm(~[`X,`Y])), [-pi,pi],[-2pi,2pi])
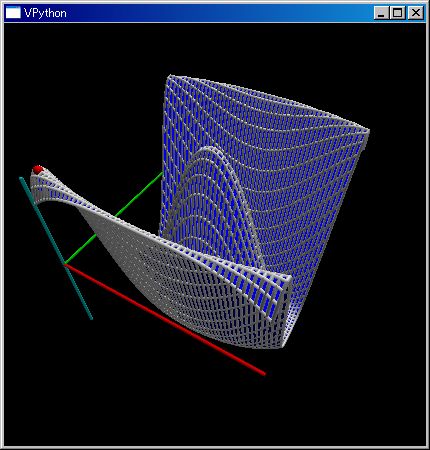
複素領域を指定すると、位相回転を RGB の混ざり具合であらわし絶対値を z 軸の値とした kkRGB 表示を行います。
plot3dGr(`X^2 + `X + 1, [-1,1],[-`i,`i], )
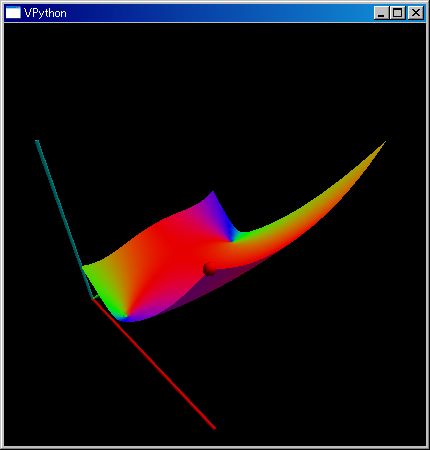
三次元行列データ表示 renderMtrx(..)/plot3dRowCol(..) と plot3d(..)
既に何回か使いましたが renderMtrx(..) 関数の引数に行列データを与えることで、行列のインデックスを (x,y) 位置とし、行列の要素値を z 位置とする 3D グラフ表示が可能です。
kl=klsp(0,1); renderMtrx([[(λ x,y:(x^2+y))(x,y) for x in kl] for y in kl]);
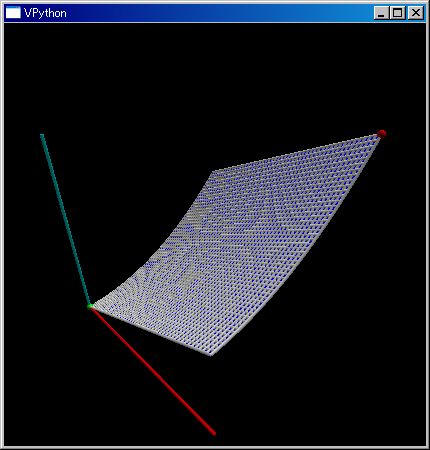
python -u sfPP.py "kl=klsp(0,1); renderMtrx([[(λ x,y:(x^2+y))(x,y) for x in kl] for y in kl]);" index:(49, 49) max: 2 index:(0, 0) min: 0
kl=klsp(0,1); plot3dRowCol([[(λ x,y:(x^2+y))(x,y) for x in kl] for y in kl]);
なぜ、全く同じ名前の関数が存在するかというと、行列データの表示には x,y 配置を 90 で変えて y,x 配置にしたときの者も必要になるからです。plot3d(..) が、そのような関数です。これらの三つの関数を適宜使い分けてください。
kl=klsp(0,1); plot3d([[(λ x,y:(x^2+y))(x,y) for x in kl] for y in kl]);
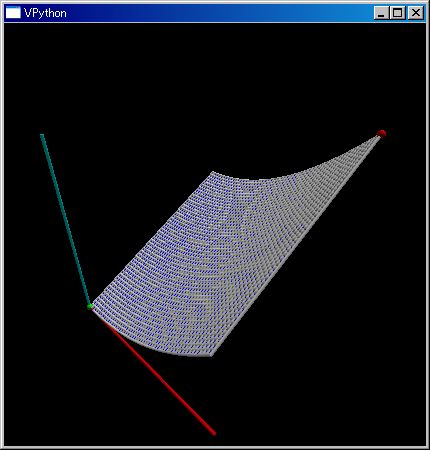
plotGr(..) のときと同様に renderMtrx(..)/plot3d(..)を複数回実行すると、複数の 3D グラフを重ねて表示します。
kl=klsp(0,1, 16); mtF=λ f:[[f(x,y) for x in kl] for y in kl]; renderMtrx(mtF(λ x,y:x^2+y));renderMtrx(mtF(λ x,y:0.5x^2+2y-0.5), color=orange)
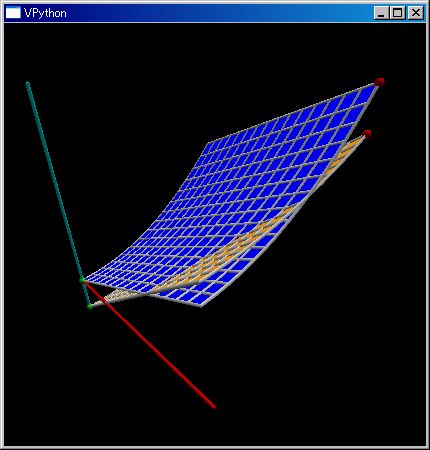
2D/3D軌跡表示 plotTrajectory(..)
plotTrajectory(..) 関数にペア・データを要素とするシーケンス・データ引数を与えることで 2d 軌跡を描けます。
plotTrajectory([(cos(θ),2 sin(θ)) for θ in klsp(0,4/3 pi)])
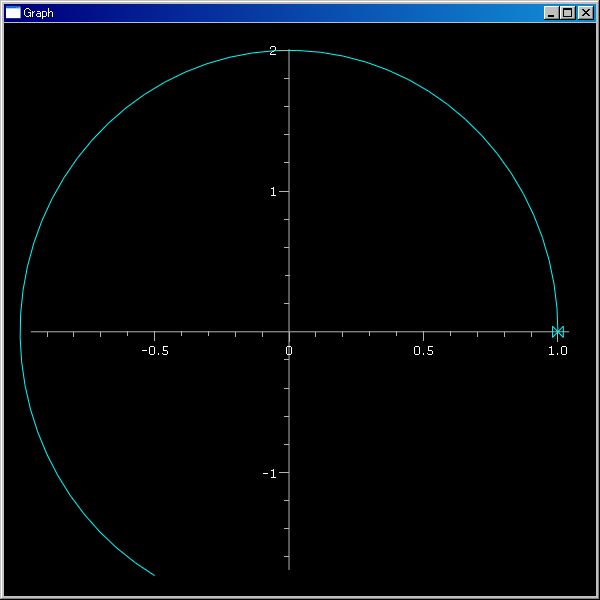
plotTrajectory(..) 関数に三つの組のデータを要素とするシーケンス・データ引数を与えることで 3d 軌跡を描けます。
plotTrajectory([(cos(θ),sin(θ),θ/20) for θ in klsp(0,6 pi)])
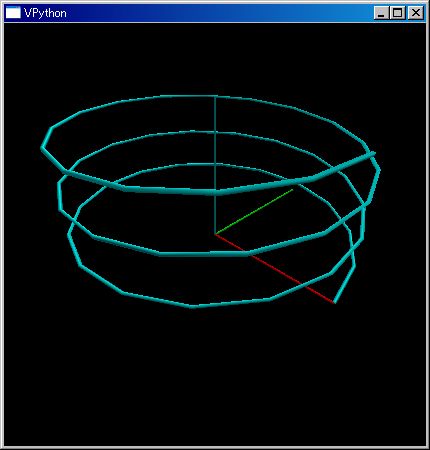
ワンライナーの最後の式の値をコンソールに自動的に出力
Python sf では、ワンライナーの式には print 文がなくても、その最終式の値をコンソールに打ち出します。これも意外と便利です。
a=3;b=4;a+b =============================== 7
「print 文が Python sf 式の中にある」、「最後の式の値が 100 x 100 行列で大きすぎる」など、最後の式の値を自動出力させたくないときは、Python sf の最後を ; にします。
for i in range(4):print 2 i 0 2 4 6 ------------------------------- None
ワンライナーの最後の式の値を _dt.pvl にも出力
Python sf は、ワンライナーの最終式の値をコンソールに打ち出すと同時に、その値をファイル変数として扱える形式で _dt.pvl にも出力します。
3+4 =============================== 7
type _dt.pvl # python object printed out by pprint 7
ファイル変数とは、Python sf がカレント・ディレクトリに作るファイルであり、また Python sf の変数として読み出せるファイルです。下のように 「=:」記号で、Python sf 式に戻すことができます。
=:_dt;_dt * 5 =============================== 35
ファイル変数とは、ファイルであり、通常の OS の command が使えます。_dt.pvl の変数名を、好みの変数名に OS command で変更できます。ただし拡張子は pvl にしておかいないと、Python sf で扱えません。
copy _dt.pvl temp.pvl /y
a =:temp;2 a =============================== 70
上で、「a =:temp」は、ファイル変数を a のラベルに付け替えています。ファイル変数は _dt.pvl とは異なり、Python sf 式の実行で勝手に書き換えられないので以前に設定された値を保ちます。何時でも再利用可能です。
=:temp;2 temp =============================== 70
_dt 以外のファイル変数名を指定できます
Python sf は、ワンライナーの最終式の値を出力先のファイル変数名を、最終文の左値に「変数 := 式」と書くことで指定できます。
test:=3+4 =============================== 7 =:test;test*5 =============================== 35
後で何度も使うファイル変数を設けたいときに := 記号を使って、明示的にファイル変数名を指定するわけです。_dt ファイル変数は、直前の Python sf ワンライナーの結果が残っているだけであり、何度も使いたいファイル変数は _dt の名前にできません。
なお、「:=」の記号の使用は、Python sf ワンライナーの途中の文でも使えます。最終文に限っていません。
ワンライナーの最後の式の値を _dt.pvl に出力できないときもあります。
残念ながら Python sf の最終式の値によっては、ファイル変数が作られないことがあります。Python sf がファイル変数を作る方法として python の pickle モジュールを利用しているからです。python が pickle できない値はファイル変数にできません。
λ x:2 x =============================== <function <lambda> at 0x0207AC30> unpicklable
Python では、関数自体は pickel できないので、最終式の値が関数自体のときは _dt.pvl は空ファイルになります。
以上のことを知っていれば、Python sf を電卓的な計算に使い始めらると思います。Mathematica ゃ Matlab などの計算ソフトをインストールしていながら その横で電卓計算をしているようなことはなくなると思います。
でも Python sf の利用は、そのような単純な段階に留めるべきではありません。次は、Python sf らしい、より高度な使い方に挑戦してみましょう。
■■ Python sf による少し高度な計算
Python sf は単なる電卓ソフトではありません。十分にすぎるほどに高度・複雑な計算も対象にできます。それらを最小の手間で計算することを追及しています。以下では電卓を超えた、もう少し Python sf の使い方を見ていきます。
■ ワンライナーでの行列計算
まずは広く活用される行列について、もう少し詳しく見ていきましょう。Python sf では、ベクトルや行列の生成を ~[...] の簡便な記述で可能にしています。Python でのリスト記述の最初に ~ 記号を付けるだけです。Python プリプロセッサが、簡便な ~[....] Python sf 式記述を Python 関数に変換し、Python に処理させます。デフォルトで float/complex 型の値を要素とするベクトルや行列になります。それ以外の、例えばint:整数型や一般体のベクトル/行列などを生成させるためには、型を指定する必要があります。
~[1,2,3] # float vector =============================== [ 1. 2. 3.] ---- ClTensor ---- ~[1,2+0j,3] # complex vector =============================== [ 1.+0.j 2.+0.j 3.+0.j] ---- ClTensor ---- ~[[1,2,3],[4,5,6]] # 2 x 3 float matrix =============================== [[ 1. 2. 3.] [ 4. 5. 6.]] ---- ClTensor ---- ~[[1,2,3],[4,5,6], int] # 2x3 integer matrix =============================== [[1 2 3] [4 5 6]] ---- ClTensor ---- ~[1,2,3] ^ ~[4,5,6] # diadic product |v1><v2| =============================== [[ 4. 5. 6.] [ 8. 10. 12.] [ 12. 15. 18.]] ---- ClTensor ---- `σx ^ `σy # extention of diadic product: =============================== [[[[ 0.+0.j 0.+0.j] [ 0.+0.j 0.+0.j]] [[ 0.+0.j 0.-1.j] [ 0.+1.j 0.+0.j]]] [[[ 0.+0.j 0.-1.j] [ 0.+1.j 0.+0.j]] [[ 0.+0.j 0.+0.j] [ 0.+0.j 0.+0.j]]]] ---- ClTensor ---- # 行列どうしの ^ 演算について、一要素について確認 i,j,k,l=0,1,1,0; (`σx ^ `σy)[i,j,k,l] == `σx[i,j] `σy[k,l] =============================== True # 行列どうしの ^ 演算について、全ての要素について確認 lst=(0,1);all([(`σx ^ `σy)[i,j,k,l] == `σx[i,j] `σy[k,l] for i,j,k,l in mitr(lst,lst,lst,lst)]) =============================== True # 上の式の意味を理解してもらえれば、行列どうしの ^ 演算の意味を理解してもらえるでしょう。 # ^ 演算子は一般相対論でのテンソル計算で活躍します。
行列・ベクトル・係数体の組み合わせに対して、線形代数で定義されている加減乗除算が行えます。乗算演算子:* は、通常の数式の時のように省略可能です。
~[1,2,3]+~[4,5,6] # add vectors =============================== [ 5. 7. 9.] ---- ClTensor ---- 3 *~[1,2,3] # scalar * matrix =============================== [ 3. 6. 9.] ---- ClTensor ---- 3 ~[1,2,3] # multiply without the * operator =============================== [ 3. 6. 9.] ---- ClTensor ---- mt=~[[1,2],[3,4]]; mt mt # matrix * matrix =============================== [[ 7. 10.] [ 15. 22.]] ---- ClTensor ----Python sf でのベクトル同士の積は内積の意味になります。
a =~[1,2,3];b=~[4,5,6];a b # <a | b> =============================== 32.0 a =~[1,2,3];b=~[4,5,6];(a + b) b # <a+b | b> =============================== 109.0
行列とベクトルの掛け算も積演算子で表現され、その積演算子を省略可能です。
mt=~[[1,2],[3,4]]; v=~[1,2];mt v =============================== [ 5. 11.] ---- ClTensor ---- mt=~[[1,2],[3,4]]; v=~[1,2];2 mt*v =============================== [ 10. 22.] ---- ClTensor ----
ただし、Python sf では縦ベクトル/横ベクトルの区別がありません。「ベクトル*行列」の積もサイズさえ合えば計算できます。
mt=~[[1,2],[3,4]]; v=~[1,2];2 v mt =============================== [ 14. 20.] ---- ClTensor ---- mt=~[[1,2],[3,4]]; v=~[1,2];2 v mt + v =============================== [ 15. 22.] ---- ClTensor ----
ですから、ディラック表記 <v|mt|v> のような計算もできてしまいます。
mt=~[[1,2],[3,4]]; v=~[1,2];2 v mt v # this means <v|mt|v> =============================== 54.0
ただし複素ベクトルでの <v|v>, <v|mt|v> 計算で、自動的に共役ベクトルに変換することはありません。ユーザーが .d をベクトルの後に付けて、明示的に共役ベクトルに変換しなければなりません。
~[1+2`i, 3+4`i] ~[0+1`i, 2+3`i] =============================== (-8+18j) v=~[1+2`i, 3+4`i]; v v =============================== (-10+28j) v=~[1+2`i, 3+4`i]; v.d v =============================== (30+0j) mt=~[[1,2],[3,4]]; v=~[1+2j,2];2 v.d mt v # this means <v|mt|v> =============================== (62+8j) mt=~[[1,2],[3,4]]; v=~[1+2j,2];2 v mt v # this dose not means <v|mt|v> =============================== (46+48j)
べき乗演算子は「^」と「**」の両方が使えます。Python では「**」がべき乗で「^」は bit xor なのですが、Python sf では「^」もべき乗にしています。数学では「^」をべき乗にすることが多いからです。この処理はプリプロセッサに行わせています。プリプロセッサを使わないときは、べき乗には ** 演算子しか使えません。
mt=~[[1,2],[3,4]]; mt^2 =============================== [[ 7. 10.] [ 15. 22.]] ---- ClTensor ---- mt=~[[1,2],[3,4]]; mt**2 =============================== [[ 7. 10.] [ 15. 22.]] ---- ClTensor ---- mt=~[[1,2],[3,4]]; mt^8 =============================== [[ 165751. 241570.] [ 362355. 528106.]] ---- ClTensor ----逆行列は /,**,^ 演算子を使って表記できます。
mt=~[[1,2],[3,4]]; mt^-1 =============================== [[-2. 1. ] [ 1.5 -0.5]] ---- ClTensor ---- mt=~[[1,2],[3,4]]; mt**-1 ============================== [[-2. 1. ] [ 1.5 -0.5]] ---- ClTensor ---- mt=~[[1,2],[3,4]]; 1/mt ============================== [[-2. 1. ] [ 1.5 -0.5]] ---- ClTensor ---- mt=~[[1,2],[3,4]]; v=~[1,2];mt/mt ============================== [[ 1.00000000e+00 0.00000000e+00] [ 8.88178420e-16 1.00000000e+00]] ---- ClTensor ---- mt=~[[1,2],[3,4]]; v=~[1,2];mt mt^-1 ============================== [[ 1.00000000e+00 0.00000000e+00] [ 8.88178420e-16 1.00000000e+00]] ---- ClTensor ---- mt=~[[1,2],[3,4]]; v=~[1,2];mt^-1 mt ============================== [[ 1.00000000e+00 0.00000000e+00] [ 2.22044605e-16 1.00000000e+00]] ---- ClTensor ---- mt=~[[1,2],[3,4]]; v=~[1,2];2 mt^-1 v =============================== [ 0. 1.] ---- ClTensor ---- mt=~[[1,2],[3,4]]; v=~[1,2];v/mt =============================== [ 1. 0.] ---- ClTensor ----
リスト内包表記の角括弧の先頭に ~ 記号を付けたものも Python sf 行列になります。これは結構便利です。リスト内包表記の簡潔な記述とドキュメント性の高さが、行列・ベクトル表記にも適用できるからです。
~[k^2 for k in range(5)] =============================== [ 0. 1. 4. 9. 16.] ---- ClTensor ---- ~[[k^2+p for k in range(5)]for p in range(3)] =============================== [[ 0. 1. 4. 9. 16.] [ 1. 2. 5. 10. 17.] [ 2. 3. 6. 11. 18.]] ---- ClTensor ----
numpy 行列 ベクトル
scipy,numpy で用意している array 行列・ベクトルを使いたいときは sc.array(...) で行列・ベクトルを使います。「sc.」のラベルを前に付けることで s numpy の名前空間にある機能全てを扱えます。
vct = sc.array([1,2,3]) =============================== [1 2 3] vct = sc.array([1,2,3]); 2 vct =============================== [2 4 6]
ただし sc.array と ClTensor の演算では微妙な違いがあります。scipy,numpy に詳しくないうちは sc.array(..) の使用を控えることを勧めます。
例えば sc.array(..) でのベクトルどうしの * 演算は要素ごとの積をとったベクトルになります。内積を計算させるには sc.dot(..) 関数を使います。
vct=sc.array([1,2,3]); vct * vct =============================== [1 4 9] vct=sc.array([1,2,3]); vct vct =============================== [1 4 9] vct=sc.array([1,2,3]); sc.dot(vct, vct) =============================== 14
---- ClTensor ---- についてPython sf でのベクトル・行列のコンソール出力で「---- ClTensor ----」が出てくるのは、後で出てくる scipy の array, 一般体向けの ClFldTns と区別するためです。二階までのベクトル・行列については matrix やベクトルの性質を持ちます。三階以上の ClTensor については逆行列が定義できませんが、加減乗算が定義できます。テンソルとしての演算が可能です。
ClTensor の名前にしたのは、一般相対論での Christoffel 接続係数や Rieman テンソルを扱いたいこともあるのですが、既に Numpy にある Matrix クラスと混同させたくないこともありました。
不必要な心配をさせたかも知れませんが、ご理解ください。
Pauli 行列 / Levi Civita テンソル
customize.py にはユーザーが頻繁に使う変数や完遂を定義できます。Python sf を実行開始するときに customize.py に定義してある変数名を定義済みの名前として取り込みます。
後々行列、テンソル計算の説明に便利なので、ここで、customize.py に定義してある Pauli 行列とその計算例を示しておきます。customize.py の中で、 Pauli 行列として `σx, `σy, `σx の変数名で下のような行列を対応させてあります。これを Python sf の定義済み変数として下のように扱えます。「import customize」はプリプロセッサ側が自動的に行います。またプリプロセッサを介することで Python 2.5/2.6 であってもギリシャ文字の漢字を使えます。(まだ Python 3000 での Python sf 実装は行っていません)
`σx =============================== [[ 0. 1.] [ 1. 0.]] ---- ClTensor ---- `σy =============================== [[ 0.+0.j 0.-1.j] [ 0.+1.j 0.+0.j]] ---- ClTensor ---- `σz =============================== [[ 1. 0.] [ 0. -1.]] ---- ClTensor ----
上の Python sf 式で backquote:「`」は Python の名前空間を広げるためにプリプロセッサ側で処理しています。変数名の前後に複数の ` を追加できるようにしています。
Python sf 式を実行する直前に、プリプロセッサは coustomize.py を import するので、定義済みの Pauli 行列を組み合わせた加減乗除べき乗算が可能です。
`σx + 2 `σy + `σy^2 `σz + 10 `σz =============================== [[ 11.+0.j 1.-2.j] [ 1.+2.j -11.+0.j]] ---- ClTensor ----
Hamilnonian 行列 `σx+`σy+`σz の時刻 t = 0.1 のときの exp を、上のように計算させられます。`i は 1j と Python 流に書いても言いのですが `i の方が数学での純虚数表記に近いので customize.py の中でユーザー変数として定義しました。
H = `σx + `σy + `σz; t=0.1;logm(`i t H) =============================== [[-1.75327895+0.90689968j 0.90689968+0.90689968j] [-0.90689968+0.90689968j -1.75327895-0.90689968j]] ---- ClTensor ---- H = `σx + `σy + `σz; t=0.1;expm(`i t H) =============================== [[ 0.98503746+0.09950075j 0.09950075+0.09950075j] [-0.09950075+0.09950075j 0.98503746-0.09950075j]] ---- ClTensor ----
i を純虚数の記号として使えればよいのですが、文字 i はインデックスなど Python のコードで別の意味に使われることがあり、変数の衝突が発生するので短い i 一文字に純虚数を割り当てられません。でも backquote:` を i の前に追加した変数ならば Python コードのインデックス i と衝突することはありません。「`i」 ならば数式の中で純虚数の意味であることも可読性良く表記できます。
ゼロ行列、単位行列
kzrs(shape引数,type) により 0 行列を生成します。ベクトルを生成するときは kzrs の shape 引数に一つだけのベクトルサイズ整数を指定します。デフォルトのタイプは実数です。
kzrs(3,4) =============================== [[ 0. 0. 0. 0.] [ 0. 0. 0. 0.] [ 0. 0. 0. 0.]] ---- ClTensor ---- kzrs(5) =============================== [ 0. 0. 0. 0. 0.] ---- ClTensor ---- kzrs(2,3,4) [[[ 0. 0. 0. 0.] [ 0. 0. 0. 0.] [ 0. 0. 0. 0.]] [[ 0. 0. 0. 0.] [ 0. 0. 0. 0.] [ 0. 0. 0. 0.]]] ---- ClTensor ---- kzrs(3,4, int) =============================== [[0 0 0 0] [0 0 0 0] [0 0 0 0]] ---- ClTensor ---- kzrs(3,4, complex) =============================== [[ 0.+0.j 0.+0.j 0.+0.j 0.+0.j] [ 0.+0.j 0.+0.j 0.+0.j 0.+0.j] [ 0.+0.j 0.+0.j 0.+0.j 0.+0.j]] ---- ClTensor ----
int 行列要素に実数値を代入すると、小数点以下が切り捨てられます。御注意ください。
vc=kzrs(3,int);vc[0]=3.142;vc =============================== [3 0 0] ---- ClTensor ---- vc=kzrs(3);vc[0]=3.142;vc =============================== [ 3.142 0. 0. ] ---- ClTensor ----
単位行列を生成するには、正方 0 行列を生成し、それの 0 べき乗を計算させます。
kzrs(3,3)^0 =============================== [[ 1. 0. 0.] [ 0. 1. 0.] [ 0. 0. 1.]] ---- ClTensor ---- kzrs(3,3,int)^0 =============================== [[1 0 0] [0 1 0] [0 0 1]] ---- ClTensor ----
行列やベクトルのスライス
行列/ベクトルの部分行列/部分ベクトルを まとめてアクセスするのに : 記号を使います。vector[startIndex:endIndex] のように使います。ベクタのときはリストと同じです。startIdex を省略したときは 0 になります。endIndex を省略したときは最後までを意味します。マイナスのインデックスは最後から数えたインデックスを意味します。
# list range(10) =============================== [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] range(10)[3:6] =============================== [3, 4, 5] range(10)[:3] =============================== [0, 1, 2] range(10)[6:] =============================== [6, 7, 8, 9] range(10)[6:-2] =============================== [6, 7] # vector ~[range(10)] =============================== [ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9.] ---- ClTensor ---- ~[range(10)][3:6] =============================== [ 3. 4. 5.] ---- ClTensor ---- ~[range(10)][:3] =============================== [ 0. 1. 2.] ---- ClTensor ---- ~[range(10)][6:] =============================== [ 6. 7. 8. 9.] ---- ClTensor ---- ~[range(10)][6:-2] =============================== [ 6. 7.] ---- ClTensor ---- #matrix mt=~[range(4*4)].reshape(4,4);mt =============================== [[ 0. 1. 2. 3.] [ 4. 5. 6. 7.] [ 8. 9. 10. 11.] [ 12. 13. 14. 15.]] ---- ClTensor ---- mt=~[range(4*4)].reshape(4,4);mt[1:3,2:4] =============================== [[ 6. 7.] [ 10. 11.]] ---- ClTensor ---- mt=~[range(4*4)].reshape(4,4);mt[1:3,:] =============================== [[ 4. 5. 6. 7.] [ 8. 9. 10. 11.]] ---- ClTensor ----
[startIndex:stopIndex:stepIdex] のインデックスの指定のしかたで、 step 分だけ飛ばした取り出し方もできます。 特別記法なのですが「::-1] のインデックスの書き方をすると反転させることを意味します。
range(10)[2:8:3] =============================== [2, 5] ~[range(10)][2:8:3] =============================== [ 2. 5.] ---- ClTensor ---- range(10)[::-1] =============================== [9, 8, 7, 6, 5, 4, 3, 2, 1, 0] vc=~[range(10)];vc[::-1] =============================== [ 9. 8. 7. 6. 20. 4. 3. 10. 1. 0.] ---- ClTensor ----
[startIndex:stopIndex:stepIndex] での要素アクセスは、行列要素への代入にも使えます
vc=~[range(10)];vc[2:8:3]=[10,20]; vc =============================== [ 0. 1. 10. 3. 4. 20. 6. 7. 8. 9.] ---- ClTensor ---- mt=~[range(4*4)].reshape(4,4);mt[1:3,2:4]=[[10,20],[30,40]]; mt =============================== [[ 0. 1. 2. 3.] [ 4. 5. 10. 20.] [ 8. 9. 30. 40.] [ 12. 13. 14. 15.]] ---- ClTensor ----
スライス操作による行列やベクトルの切り出しは、元のデータのコピーではなく、元データの参照を切り出していることを知っておくべきです。
mt=~[range(4*4)].reshape(4,4);mtSub=mt[1:3,2:4];mtSub[:,:]=[[100,200],[300,400]];mt =============================== [[ 0. 1. 2. 3.] [ 4. 5. 100. 200.] [ 8. 9. 300. 400.] [ 12. 13. 14. 15.]] ---- ClTensor ----
シーケンス・データの ::-1 スライスにより、データの並びを反転できましたが、それを行列やベクトルにも適用できます。
range(5) =============================== [0, 1, 2, 3, 4] range(5)[::-1] =============================== [4, 3, 2, 1, 0] ~[range(5)] =============================== [ 0. 1. 2. 3. 4.] ---- ClTensor ---- ~[range(5)][::-1] =============================== [ 4. 3. 2. 1. 0.] ---- ClTensor ---- mt=~[range(4*5)].reshape(4,5); mt =============================== [[ 0. 1. 2. 3. 4.] [ 5. 6. 7. 8. 9.] [ 10. 11. 12. 13. 14.] [ 15. 16. 17. 18. 19.]] ---- ClTensor ---- mt=~[range(4*5)].reshape(4,5); mt[::-1] =============================== [[ 15. 16. 17. 18. 19.] [ 10. 11. 12. 13. 14.] [ 5. 6. 7. 8. 9.] [ 0. 1. 2. 3. 4.]] ---- ClTensor ---- mt=~[range(4*5)].reshape(4,5); mt[::-1, ::-1] =============================== [[ 19. 18. 17. 16. 15.] [ 14. 13. 12. 11. 10.] [ 9. 8. 7. 6. 5.] [ 4. 3. 2. 1. 0.]] ---- ClTensor ---- mt=~[range(4*5)].reshape(4,5); mt[:, ::-1] =============================== [[ 4. 3. 2. 1. 0.] [ 9. 8. 7. 6. 5.] [ 14. 13. 12. 11. 10.] [ 19. 18. 17. 16. 15.]] ---- ClTensor ----
これを使えば、ベクトルの convolution 演算などが簡単にできます。
vcL, vcR = ~[range(8)], ~[range(0,80,10)];~[vcL[:k][::-1] vcR[:k] for k in range(1,8+1)] =============================== [ 0. 0. 10. 40. 100. 200. 350. 560.] ---- ClTensor ---- # 別の畳み込み計算 vcL, vcR = ~[range(8)], ~[range(0,80,10)];sc.convolve(vcL, vcR) =============================== [ 0. 0. 10. 40. 100. 200. 350. 560. 840. 1040. 1150. 1160. 1060. 840. 490.]
■ 階層構造を持った名前空間
デフォルトの Python sf はグローバル名前空間と、下の赤で示されるサブの名前空間からなる名前空間の階層構造を持ちます。この名前空間の構造はユーザーカスタマイズ可能です。でも Python sf の高度な活用のためには、デフォルトの名前空間の構造、すなわちグローバル名前空間に属するクラス・関数群、各サブ名舞う空間に属するクラス・関数群をイメージできるようになることが必須です。
┌──────────────────┐ │ Python sf │┌─────────────────────┐ │ sfPPrcssr 一万行以上 の ││sc:numpy: 行列計算パッケージ │ │ Pre - processor ││sy:scipy: Matlab 相当の数値計算パッケージ │ │ ││ts:sympy: シンボリック数式処理パッケージ │ │ Global:sfFnctns:.行列の拡張 ││vs:vpython:2D/3D 表示パッケージ │ │ basicFnctns ││mlb:maysvi 2d/3d 表示パッケージ │ │ kNumeric 微分・積分拡張 │└─────────────────────┘ │ vsGraph 簡便なグラフ表示 │┌────────────────────┐ │ rational 有理式 ││既存のーザー側で用意する pythonライブラ │ │ Global:customize.py ││リ・パッケージ │ │ Global:sfCrrntIni.py │└────────────────────┘ │ ユーザー・カスタマイズ │┌────────────────────┐ │ oc:octn.py ││ユーザー側で開発する python │ │ 八元数 ││モジュール・パッケージ │ │ Bool 体 │└────────────────────┘ │ GF(2^8) Galois 体 │ │ Zp, Sn │ │ │ │ tc:tlRcGn │ │ 無限数列 │ │ 末尾再帰 │ │ │ │ kre:kre 正規表現 │ │ │ kv:kv kVerifier test library │ │ │ └──────────────────┘
グローバル名前空間
Python sf はグローバル名前空間に sin.cos などの基本数値関数や plotGr(..) などといった計算に必須の関数を数多く設定しています。
Python sf プリプロセッサは、与えられた計算式を実行する前に、下のモジュールをグローバル名前空間に取り込んでいます。このおかげで mrng, sin, cos, plotGr などの確約する関数群を Python sf で直に呼び出せています。ts などのサブ名前空間の指定無しで呼び出せています。
- sfFnctns.pyc --- ClTensor:整数・実数・複素数行列, ClFldTns:一般体行列, ...
- basicFnctns.py --- Python sf 制御のための基本的な関数 arsq(..),mrng(..),mitr(..), ...
- kNumeric.py --- 数値計算 sin(..), cos(..),
- vsGraph.py --- グラフ表示 plotGr(..), plot3dGr(..), renderMtrx(..) ...
- rational.py --- 線形システムのための有理関数 ClRtnl
サブ名前空間 sc
でも、全てをグローバル名前空間に取り込み、直接呼び出せば良いものではありません。人間の記憶力には限りがあります。でも記憶しきれないからといって、関数名や変数名の衝突により予想外の動作が紛れ込むなど論外です。そのため名前空間に階層構造を入れ、サブの名前空間からアクセスすることが必要となります。
例えば numpy package の下にある関数やクラス群は sc サブ名前空間の下でアクセスします。下のような具合です。
# numpy 配列の生成 sc.arange(10) =============================== [0 1 2 3 4 5 6 7 8 9] sc.arange(4*5).reshape(4,5) =============================== [[ 0 1 2 3 4] [ 5 6 7 8 9] [10 11 12 13 14] [15 16 17 18 19]] # numpy 行列とリストの積 sc.dot(sc.arange(4*5).reshape(4,5), [0,1,2,3,4]) =============================== [ 30 80 130 180] # numpy 0 行列の生成 sc.zeros([3,5]) =============================== [[ 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0.]]
~[range(4*5)].reshape(4,5) =============================== [[ 0. 1. 2. 3. 4.] [ 5. 6. 7. 8. 9.] [ 10. 11. 12. 13. 14.] [ 15. 16. 17. 18. 19.]] ---- ClTensor ---- ~[range(4*5)].reshape(4,5) [0,1,2,3,4] =============================== [ 30. 80. 130. 180.] ---- ClTensor ----
でも numpy 行列・ベクトルを使ったほうが良いときも発生します。例えば、ベクトルとベクトルの積を内積ではなく、要素どおしの積からなるベクトルにしたいことがあります。ClTensor, ClFldTns でのベクトルの積は内積の意味になっています。これらでは要素どおしの積からなるベクトルを作るのは、少し面倒です。
そのときは「sc.」 のサブ名前空間の下に numpy の名前空間が収まっていると看做して numpy の関数やクラスを呼び出してください。「sc.」の三文字を先頭に付けるだけなら、手間も殆どかかりません。
vcA,vcB=sc.arange(3), sc.arange(1,4);vcA, vcB =============================== (array([0, 1, 2]), array([1, 2, 3])) #要素どおしの積からなるベクトルの計算 vcA,vcB=sc.arange(3), sc.arange(1,4);vcA vcB =============================== [0 2 6] # ClTensor でのベクトルの積の計算は内積になる vcA,vcB=~[range(3)], ~[range(1,4)];vcA vcB =============================== 8.0 # ClTensor では少し面倒な、要素どおしの積からなるベクトルの計算 vcA,vcB=~[range(3)], ~[range(1,4)];~[vcA[k] vcB[k] for k in range(3)] =============================== [ 0. 2. 6.] ---- ClTensor ---- vcA,vcB=~[range(3)], ~[range(1,4)];sc.array(vcA) sc.array(vcB) =============================== [ 0. 2. 6.]
その他のデフォルトで組み込まれるサブ名前空間
Python sf は oc, tn のサブ名前空間の名前で octn, tlRcGn モジュールを取り込んでいます。
- oc 代数系のクラス群:octn.py ブール代数体:BF, 八元数:ClOctonion, Zp(N) 整数有限体:Zp(..), ...
- tn tlRcGn.py 無限繰り返し処理のクラス、ジェネレータ群:counter(..), repeat(..), ...
- kre kre.py 正規表現クラス
ダイナミックな package サブ名前空間の取り込み
サブ名前空間に別の package をわり当てることもできますが、大きな package のときは、その import だけで下手をしたら一秒以上の時間が掛かってしまいます。使わない package を無条件に import させていては、Python sf 式の計算時間の何倍も、これらの import のために時間をとられてしまいます。下手をすると秒のオーダーで import だけに時間をとられます。scipy, sympy, visual, mayavi.mlab のような、計算ソフトには有用だがimport に時間の掛かる package は、下の専用関数を用意して ユーザーが必要となるたびに明示的に呼び出すようにしています。
- sy() --- サブ名前空間 sy: scipy package
- ts() --- サブ名前空間 ts: sympy package
- vs() --- サブ名前空間 vs: visual package
- mlb() --- サブ名前空間 mlb: mayavi.mlab package
ユーザーによるモジュール・インポート
Python には、有用なモジュールが既に大量に蓄積されています。全世界の Python を好きなハッカーたちが使い切れない有用なモジュールをフリーで使えるようにしてくれています。それらを python sf でも自由に利用できます。
例えば標準の python に calendar.py モジュールが入っています。これを使えば任意の年の曜日と日付が分ります。calender.py の機能は「import calender」を行うだけで利用できるようになります。calender には以下の機能が備わっています。
import calendar as cl;help(cl)
・
・
FUNCTIONS
calendar = formatyear(self, theyear, w=2, l=1, c=6, m=3) method of TextCalendar instance
Returns a year's calendar as a multi-line string.
firstweekday = getfirstweekday(self) method of TextCalendar instance
isleap(year)
Return 1 for leap years, 0 for non-leap years.
leapdays(y1, y2)
Return number of leap years in range [y1, y2).
Assume y1 <= y2.
month = formatmonth(self, theyear, themonth, w=0, l=0) method of TextCalendar instance
Return a month's calendar string (multi-line).
monthcalendar = monthdayscalendar(self, year, month) method of TextCalendar instance
Return a matrix representing a month's calendar.
Each row represents a week; days outside this month are zero.
monthrange(year, month)
Return weekday (0-6 ~ Mon-Sun) and number of days (28-31) for
year, month.
prcal = pryear(self, theyear, w=0, l=0, c=6, m=3) method of TextCalendar instance
Print a year's calendar.
prmonth(self, theyear, themonth, w=0, l=0) method of TextCalendar instance
Print a month's calendar.
setfirstweekday(firstweekday)
timegm(tuple)
Unrelated but handy function to calculate Unix timestamp from GMT.
weekday(year, month, day)
Return weekday (0-6 ~ Mon-Sun) for year (1970-...), month (1-12),
day (1-31).
この calender.py モジュールを明示的に import することで、指定の月の曜日を次のようなワンライナーで表示させられます。
import calendar as cl;cl.prmonth(2010,5)
May 2010
Mo Tu We Th Fr Sa Su
1 2
3 4 5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20 21 22 23
24 25 26 27 28 29 30
31
===============================
None
「from moduleOrPackageName import *」とすることで、moduleOrPackageName にある関数や変数をグローバル名前空間に取り込みます。こうするとモジュール名を指定することなく「variable」などと利用できるようになります。使用頻度の高い関数や変数名をグローバル名前空間に置きます。calender module の場合は下のようになります。
from calendar import *; prmonth(2010,5)
May 2010
Mo Tu We Th Fr Sa Su
1 2
3 4 5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20 21 22 23
24 25 26 27 28 29 30
31
===============================
None
最小の標準の python でさえ、使い切れない面白い機能が詰まっています。まして Enthought のような、多くの機能を寄せ集めたパッケージでは、その一割の機能さえ使いこなすことが難しい程に多くのモジュールが詰め込まれています。それらを探して使うだけで多くのことが Python sf ワンライナーで書けます。
例えば四元数を扱いたかったとしましょう。それを扱っている python ソースの中には quaternion の文字が入っているはずです。そんなファイルが Python ディレクトリの中にあることを Windows では findstr コマンドで調べられます。
findstr /n /i /s /c:"quaternion" \lng\python26\*.py \lng\python26\Lib\site-packages\Editra\src\extern\pygments\lexers\other.py:1128: r'precision|pwr|quadratic_spline|quaternion|quick_color|' \lng\python26\Lib\site-packages\enthought\mathematics\api.py:8:from quaternion import normq, qmult, rotmat, rotquat \lng\python26\Lib\site-packages\enthought\mathematics\quaternion.py:8:""" Provides functions that manipulate quaternions. \lng\python26\Lib\site-packages\enthought\mathematics\quaternion.py:10: Quaternions are frequently used to avoid 'gimbal lock' and/or 'twisting' \lng\python26\Lib\site-packages\enthought\mathematics\quaternion.py:20: Normalize a quaternion. \lng\python26\Lib\site-packages\enthought\mathematics\quaternion.py:30: Multiply two quaternions. \lng\python26\Lib\site-packages\enthought\mathematics\quaternion.py:43: Transform a unit quaternion into its corresponding rotation matrix (to \lng\python26\Lib\site-packages\enthought\mathematics\quaternion.py:75: Compute the quaternion that rotates the normalized vector *vhat1* to *vhat2*. \lng\python26\Lib\site-packages\enthought\mathematics\quaternion.py:77: The quaternion is repesented as a tuple (scalar part, vector part). \lng\python26\Lib\site-packages\pygments\lexers\other.py:1202: r'precision|pwr|quadratic_spline|quaternion|quick_color|' \lng\python26\Lib\site-packages\pysf\octn.py:39: """' Octonion class including quaternion, complex, and real numbers \lng\python26\Lib\site-packages\pysf\octn.py:51: declaration of quaternion
Enthought Python Distribution の中に含まれる module,package は Enthougt が有用だと判断した、また配布する python のバージョンでの動作を確認したものが入っています。組み合わせ動作も含めて正常に動作をするとものが、まとめられています。
標準 Python の配布元で纏めている Package Index にも数多くの多様な分野の python プログラムが集められています。これらのモジュールを使うときにはバージョンに注意する必要が有りますが、概ね動くと思われます。Python は upper compatible なバージョンアップをしてきているからです。ここに集められた Python プログラムは、既に多くのユーザーに使われた実績のあるものであり、不必要なバグに悩まされることは少ないでしょう。
さらに google で検索をかければ、もっと多くのコードが見つかります。小さなプログラムならばバグがあっても自分で対処できます。スクラッチからコードを書くよりは、ずっと楽です。たいていの Python のコードが、C のコードの何倍も読みやすくなっています。強制インデントと、ドキュメント性とコードのコンパクト性を両立させている Python 言語の素晴らしさです。これらの多くが 100 行以下であり、そのまま使えなくても、ソース・コードに手を加えれば自分の望むようにできることが多いものです。
Python sf のカスタマイズ
必要な計算機能はユーザーごとに異なります。そしてワンライナーで、コンパクトに かつ多分野の計算式を記述するには、ユーザーごとにカスタマイズすることが必須となります。
Python sf のプリプロセッサは、Python sf 式を実行する前に pysf ディレクトリにある costomize.py モジュールをグローバル名前空間に取り込みます。その次にカレント・ディレクトリに sfCrrntIni.py ファイルがあれば、それをグローバル名前空間に取り込みます。この二つのモジュールの中にユーザーが必要な関数やクラスや変数を定義すれば、それらは Python sf のグローバル名前空間にとりこまれます。Python sf 式で直に呼び出せるようになります。
customize.py,sfCrrntIni.py の中で「import moduleOrPackage as mp」を行わせれば mp 名前空間の下に moduleOrPackage が配置されます。ユーザーの望む module/package が mp の名前の下で扱えるようになります。
customize.py によるカスタマイズ
customize.py には、Python sf 全般に共通するカスタマイズするためのコードを記述します。Python sf プロプロセッサは「from customize import *」を実行してから Python sf 式:ワンライナーを呼び出します。これにより Python sf 式:ワンライナーは、customize.py に定義してある変数名を定義済みとして扱えます。
例えば純虚数の Python sf 記号に「`i」を使えるのは下の Python 式が customize.py の中に書いてあるからです。
k__bq_i___ = 1j # `i: imaginary unit
Python sf で「`1,`0」をブール代数の 0,1 にできるのは、customize.py の中で下のように書かれているからです。
k__bq_0___ = oc.BF(0) # Bool 0 k__bq_1___ = oc.BF(1) # Bool 1
「k__bq_」と「___」の間にユーザーの望む文字列 たとえば userName を入れて python 代入文を作れば、`userName に望みの Python 式の値を設定できます。
もちろん back quote を付けずに「userName = 式」とすることも可能です。ただし そのときは、既存の変数との衝突する可能性が高まることを覚悟しておかねばなりません。
sfCrrntIni.py によるカスタマイズ
sfCrrntIni.py は、分野ごとに使うカスタマイズ・モジュールです。ユーザーのカレント・ディレクトリごとに設けます。
Python sf プロプロセッサは、カレントディレクトリに sfCrrntIni.py ファイルが存在すると「from sfCrrntIni import *」を実行してから Python sf 式:ワンライナーを呼び出します。これにより Python sf 式:ワンライナーは、sfCrrnitIni.py に定義してある変数名を定義済みとして扱えます。
例えば群論を検討しているディレクトリに下の sfCrrntIn.py ファイルを作っておけば Sn(3), Sn(4), Sn(5) における群論の多くの性質をワンライナーで調べられるようになります。
type sfCrrntIni.py
import pysf.sfFnctns as sf
import pysf.octn as oc
S5 = oc.Sn(5)
SS5= S5.setStt
SA5=set([S5(x) for x in S5.m_tplIdxStt[:5*4*3*2//2] ])
S4 = oc.Sn(4)
SS4= S4.setStt
SA4=set([S4(x) for x in S4.m_tplIdxStt[:5*4*3*2//2] ])
S3 = oc.Sn(3)
SS3= S3.setStt
SA3=set([S3(x) for x in S3.m_tplIdxStt[:3*2//2] ])
S6 = oc.Sn(6)
#regular tetrahedron
dctP4 = { 'e':S4(0,1,2,3)
, 'a1':S4(0,2,3,1),'b1':S4(0,3,1,2)
, 'a2':S4(3,1,0,2),'b2':S4(2,1,3,0)
, 'a3':S4(1,3,2,0),'b3':S4(3,0,2,1)
, 'a4':S4(2,0,1,3),'b4':S4(1,2,0,3)
, 'hx':S4(2,3,0,1),'hy':S4(1,0,3,2),'hz':S4(3,2,1,0)}
dctP4I = dict(zip(dctP4.values(), dctP4.keys()))
この sfCrrntIn.py がカレント・ディレクトリにあれば、Sn(4) における S={S4(3, 2, 1, 0), S4(2, 3, 0, 1)} 集合の 正規化群の集合を次のワンライナーで求められます。
S={S4(3, 2, 1, 0), S4(2, 3, 0, 1)};set([ g for g in SS4 if set([g s g^-1 for s in S]) == S])
===============================
set([Sn(4)(1, 0, 3, 2), Sn(4)(2, 3, 0, 1), Sn(4)(1, 0, 2, 3), Sn(4)(3, 2, 1, 0), Sn(4)(0, 1, 2, 3), Sn(4)(3, 2, 0, 1), Sn(4)(0, 1, 3, 2), Sn(4)(2, 3, 1, 0)])
この正規化群の集合が群演算で実際に閉じていることを、下のようにワンライナーで確認できます。
S={S4(3, 2, 1, 0), S4(2, 3, 0, 1)};SS=set([ g for g in SS4 if set([g s g^-1 for s in S]) == S]);set([ x y for x,y in mitr(SS,SS)]) == SS
===============================
True
「上のような単純な群論など、とっくの昔に卒業した」という方もいるでしよう。そんな方には nzmath は如何でしょうか。 ここから nzmath package をダウンロードしてカレントディレクトリに置いておけば、Python sf で下のような計算が可能になります。nzmath package で定義された全ての変数・関数・クラスが Python sf 式で扱えるようなります。
# find cubic roots of 1 with mod 13 from nzmath import *;cubic_root.c_root_p(1,13) =============================== [1, 3, 9]
■ sfFnctns.py, basicFnctns, kNumeric.py, vsGrapy.py, raional.py
、sfFnctns.py, basicFnctns, kNumeric.py, vsGrapy.py, raional.py のファイルに書かれている名前はグローバル名前空間に取り込まれます。Python sf での計算にとって基本的な関数やクラスだからです。
basicFnctns, kNumeric, vsGrapy, raional のモジュール名もグローバル名前空間に取り込まれています。ですから、例えば help(basicFnctns) で basicFnctns に定義されているクラス・関数・定数を出力させられます。
help(basicFnctns)
Help on module pysf.basicFnctns in pysf:
NAME
pysf.basicFnctns
FILE
d:\my\vc7\mtcm\pysf\basicfnctns.py
DESCRIPTION
Designed by kVqrifierLab Kenji Kobayashi
http://www.nasuinfo.or.jp/FreeSpace/kenji/index.htm
・
・
aTrue(sqBlAg)
' make scipy.alltrue short
and counter mesure for Enthought24 below result
sc.alltrue([[True,True,True],[True,True,True]])
===============================
[True True True]
Caution! python 2.5 all can't work for scipy.array matrix
python 2.6 all can work for scipy.array matrix
'
arSqnc(startOrSizeAg, sizeAg=None, strideAg=1)
等差数列タプルを start, size, stride 引数で生成して返す
return arithmetic sequence generated with argument start, size, stride
・
・
khlp を使えば、正規表現 help 検索も可能です。 khlp('..', basicFnctns) のように検索します。
khlp('^en', basicFnctns)
python -u sfPP.py "khlp('^en', basicFnctns)"
===============================
enmasq(*args, **kwarg)
列挙インデックス付きの多次元等差数列
enumerate index and multiple dimentional arithmetic sequence
e.g.
N=4;mt=kzrs(N,N);for idx,val in enmasq([0,N,0.1],[1,N,0.1]):mt[idx]=sum(val);mt
===============================
[[ 1. 1.1 1.2 1.3]
[ 1.1 1.2 1.3 1.4]
[ 1.2 1.3 1.4 1.5]
[ 1.3 1.4 1.5 1.6]]
---- ClTensor ----
'
enmitr(*args, **kwarg)
列挙インデックス付きの多次元繰り返しイタレータ
multiple dimentional iterator with enumerate index
e.g.
s=set(['a','b']);list(enmitr(s,s))
===============================
[((0, 0), ('a', 'a')), ((0, 1), ('a', 'b')), ((1, 0), ('b', 'a')), ((1, 1), ('b', 'b'))]
s=set([1,2]);list(enmitr(s,s,s))
===============================
[((0, 0, 0), (1, 1, 1)), ((0, 0, 1), (1, 1, 2)), ((0, 1, 0), (1, 2, 1)),
((0, 1, 1), (1, 2, 2)), ((1, 0, 0), (2, 1, 1)), ((1, 0, 1), (2, 1, 2)),
((1, 1, 0), (2, 2, 1)), ((1, 1, 1), (2, 2, 2))]
'
sfFnctns.py
Python sf プリプロセッサ:sfPPrcssr.pyc は 最初に sfFnctns.pyc を import してから customize, sfCrrntIni モジュールを import して、その後に与えられたランライナー文字列のプリプロセスを行います。この sfPPrcssr.py と sfFnctns.py だけが非公開です。そのほかの全てのソースを公開しています。
sfFnctns.py のなかで basicFnctns kNumeric, vsGrapy raional モジュールを 「from moduleName import *」しています。この意味で sfFnctns.py は Python sf の大元であり、basicFnctns kNumeric, vsGrapy raional には、その次に重要な関数とクラスが書かれています。これらのモジュールの中にある関数やクラスたちはグローバル名前空間に取り込まれています。
sfFnctns.py の重要な役割として、basicFnctns kNumeric, vsGrapy raional モジュールを取り込む以外に、数値行列、一般体行列を定義することがあります。 sfFnctns.py の中では ClTensor 数値行列・ベクトルクラスが定義されています。ClTensor クラスは numpy 行列クラス sc.ndarray を継承しています。sc.ndarray が sc.dot(..) で表している演算を ClTensor では * 演算、すなわち __mul__(..) 関数に割り当てていることが sc.ndarray との一番大きな違いです。これにより、行列やベクトルの加減乗除べき乗算が日常計算により近いものになります。
#内積 vcA,vcB = ClTensor([1,2]), ClTensor([3,4]); vcA vcB =============================== 11.0 `σx =============================== [[ 0. 1.] [ 1. 0.]] ---- ClTensor ---- # 行列とベクトルの積 `σx ~[1,2] =============================== [ 2. 1.] ---- ClTensor ---- # 行列と list, tuple との積も可能です `σx [1,2] =============================== [ 2. 1.] ---- ClTensor ---- `σx (1,2) =============================== [ 2. 1.] ---- ClTensor ---- #行列の積 `σx `σy =============================== [[ 0.+1.j 0.+0.j] [ 0.+0.j 0.-1.j]] ---- ClTensor ---- # numpy 行列では内積、行列*ベクトル、行列*行列に sc.dot(,) を使います。 vcA,vcB = sc.array([1,2]), sc.array([3,4]); sc.dot(vcA, vcB) =============================== 11 mt=sc.array(`σx); sc.dot(mt, [1,2]) =============================== [ 2. 1.] mtX,mtY=sc.array(`σx),sc.array(`σy); sc.dot(mtX, mtY) =============================== [[ 0.+1.j 0.+0.j] [ 0.+0.j 0.-1.j]] # numpy 行列やベクトルの掛け算は、要素ごとを掛け算した行列やベクトルになります。 vcA, vcB =sc.array([1,2]), sc.array([3,4]); vcA vcB =============================== [3 8] mtX,mtY=sc.array(`σx),sc.array(`σy); mtX mtY =============================== [[ 0.+0.j 0.-1.j] [ 0.+1.j 0.+0.j]] mt=sc.array(`σx); mt [1,2] =============================== [[ 0. 2.] [ 1. 0.]]
Python sf は一般の体や環を要素とする行列ベクトルも扱えます。このときは ClFldTns クラスを使います。
# Bool Field インスタンスを要素とする行列の生成 ClFldTns([[`1,`1],[`0,`1]],ftype=oc.BF) # Bool Field 行列とベクトルの積 mt=ClFldTns([[`1,`1],[`0,`1]],ftype=oc.BF);mt ~[`1,`0] =============================== [1 0] ---- ClFldTns:---- mt=ClFldTns([[`1,`1],[`0,`1]],ftype=oc.BF);mt^2 =============================== [[1 0] [0 1]] ---- ClFldTns: ---- mt=ClFldTns([[`1,`1],[`0,`1]],ftype=oc.BF);mt^2 ~[`1,`0] =============================== [1 0] ---- ClFldTns: ---- mt=ClFldTns([[`1,`1],[`0,`1]],ftype=oc.BF);mt^-1 ~[`1,`0] =============================== [1 0] ---- ClFldTns: ---- mt=ClFldTns([[`1,`1],[`0,`1]],ftype=oc.BF);1/mt ~[`1,`0] =============================== [1 0] ---- ClFldTns: ---- mt=ClFldTns([[`1,`1],[`0,`1]],ftype=oc.BF);~[`1,`0]/mt =============================== [1 1] ---- ClFldTns: ----
よほど特殊な場合を除いて Python sf において行列の生成は ClTensor, ClFldTns クラスを使うのではなく ~[....] 式か、sfFnctns に定義されている krry(..) 関数を使うべきです。bool, int, float, complex のときは ClTensor に、それ以外のときは ClFldTns に自動的に krry(..) 関数の内部で切り分けるからです。ClFldTns で必須だった要素型引数を省略できるからです。
krry([1,2,3]) =============================== [ 1. 2. 3.] ---- ClTensor ---- # int type vctor krry([1,2,3], int) =============================== [1 2 3] ---- ClTensor ---- krry([0,1,2], bool) =============================== [False True True] ---- ClTensor ---- # Bool Field Tensor krry([0,1,2], oc.BF) =============================== [0 1 0] ---- ClFldTns:---- krry([1,`X,`X^2]) =============================== [ ] ---- ClFldTns: ---- unpicklable krry([1,`X,`X^2])(2) 2010,05.24 Be Cation! ClFldTns.__call__ is test implement. Not tested enough! krry([1,`s,`s^2]) =============================== [ClRtnl([ 1.],[ 1.]), ClRtnl([ 1., 0.],[ 1.]), ClRtnl([ 1., 0., 0.],[ 1.])] ---- ClFldTns: ---- krry([1,`s,`s^2])(2) 2010,05.24 Be Cation! ClFldTns.__call__ is test implement. Not tested enough! =============================== [ 1. 2. 4.] ---- ClTensor ---- krry([sin, cos, `X]) =============================== [ ] ---- ClFldTns: ---- Error in pickling krry([sin, cos, `X]) + krry([1, `X, `X^2]) =============================== [ ] ---- ClFldTns: ---- unpicklable
ClTensor はデフォルトが浮動小数点の値を要素とすることにもご注意ください。sc.array(..) はデフォルトが int です。そして int タイプの行列要素に浮動小数点値を代入すると、勝手に小数点以下が取り除かれてしまいます。整数化されてしまいます。
~[1,2] =============================== [ 1. 2.] ---- ClTensor ---- sc.array([1,2]) =============================== [1 2] vc=sc.array([1,2]);vc[1]=sqrt(2);vc =============================== [1 1]
basicFnctns
なお arsq, mrng,arsq,mitr,klsp, enmasq, enmitr のイタレータを、このモジュールで定義しています。その他に 積:product,逆関数:invF,順列・組み合わせ:permutate・combinate, シーケンスのシフト・回転:shftSq・rttSq といった基本的な可能を実装しています。
product はシーケンス・データの要素を足し合わせたものを返します。sum(..) の + の代わりに * にした働きをします。
product( (1,2,3) ) =============================== 6 product([1,2,3,4]) =============================== 24 product(~[range(1,10)]) =============================== 362880.0 product(sc.arange(1,10)) =============================== 362880
invF(関数、定義域初め、定義域終わり) は関数引数の逆関数を返します。定義域の範囲で一価関数でなければなりません。すなわち単調でなければなりません。
sin([ -pi/4, pi/4]) invF(sin, -pi/2, pi/2)(0.5) =============================== 0.523598775598 plotGr(invF(sin, -pi/2, pi/2), -1, 1)
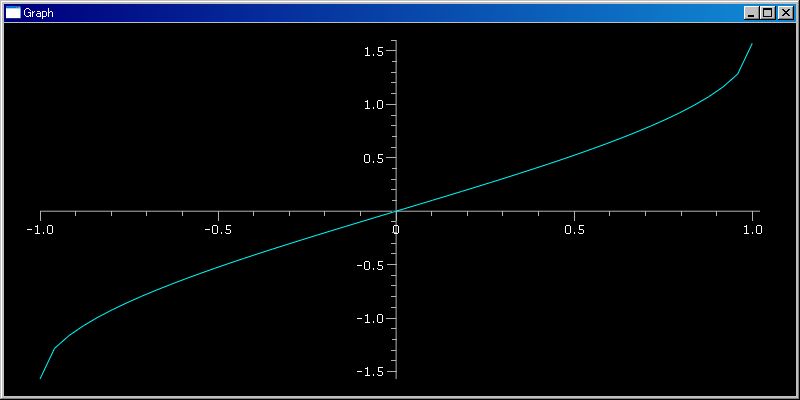
combinate(..) は n 個の組み合わせを返すジェネレータです。 辞書式順序で interte 値を返します。
list(combinate(list('abcd'),3))
===============================
[('a', 'b', 'c'), ('a', 'b', 'd'), ('a', 'c', 'd'), ('b', 'c', 'd')]
list(combinate([0,1,2,3],2))
===============================
[(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 3)]
permutate はシーケンス引数に対する順列を順次返していくイタレータを生成します。順列の入れ替えに対応する sign:-1 or 1 も返します。
tuple(sf.permutate([2,1,0]))
===============================
(((2, 1, 0), 1), ((2, 0, 1), -1), ((1, 2, 0), -1), ((1, 0, 2), 1)
, ((0, 2, 1), 1), ((0, 1, 2), -1))
tuple(sf.permutate([0,1,2]))
===============================
(((0, 1, 2), 1), ((0, 2, 1), -1), ((1, 0, 2), -1), ((1, 2, 0), 1)
, ((2, 0, 1), 1), ((2, 1, 0), -1))
shftSq(..) はシーケンスデータのシフトした値を返します。rttSq(..) はシーケンスデータを回転した値を返します。
shftSq(range(2,10)) =============================== [0, 2, 3, 4, 5, 6, 7, 8] shftSq(range(2,10),3) =============================== [0, 0, 0, 2, 3, 4, 5, 6] rttSq(range(2,10)) =============================== [9, 2, 3, 4, 5, 6, 7, 8]
関数自体の加減乗除算と `X,`Y,`Z,`T
basicFnctns モジュールには ClAF クラスが定義してあり、関数の加減乗除べき乗算と関数合成の単純記述を可能にしています。ClAF 恒等関数変数クラス・インスタンス `X を customize.py に定義することで多項式の単純な記述を可能にしました。
一般に python の関数には、関数自体を加減乗除する機能は備わっていません。しかし Python sf の基本数値関数 exp, sin, cos, tan, sinh, cosh, tanh, arcsin, arccos, arctan, log, log10, sqrt と `X,`Y,`Z,`T 恒等関数は ClAF でラップされており、加減乗除とべき乗算と関数合成機能が備わっています。これは、Python sf 式の記述の簡便な記述に重要な働きをします。λ 関数の使用を画期的に減らしてくれます。
逆に numpy の sin,cos 関数自体のの足し算はできません。それを行わせるには λ 関数を介在させる必要があります。
(sc.sin+sc.cos)(pi/3) unsupported operand type(s) for +: 'numpy.ufunc' and 'numpy.ufunc' at excecuting:(sc.sin+sc.cos)(pi/3) (λ x:sin(x)+cos(x))(pi/3) =============================== 1.36602540378
でも Python sf の ClAF でラップしてある sin,cos は加減乗除べき乗算と関数合成が可能です。
(sin+cos)(pi/3) =============================== 1.36602540378 (2 sin - 5 cos)(pi/3) =============================== -0.767949192431 #関数のべき乗 (sin^2)(pi/3) =============================== 0.761759981416 #関数合成 cos(sin)(pi/3) =============================== 0.647859344852
加減乗除べき乗算が可能な`X 恒等関数は、多項式関数の簡便な記述を可能にします。
(`X^2+ 2`X+1)(2) =============================== 9.0 ((`X+1)^2)(3) =============================== 16.0 #有理式 x=`X; ((x^2+x+1)/(2x+1))(3) =============================== 1.85714285714 多項式との関数合成 exp(-`X^2/3)(1) =============================== 0.716531310574
多変数関数と `X,`Y,`Z,`T
この機能は 2010,05,27 に実装したものであり、まだ使い込まれていません。今後修正が加わる可能性が高いままです。
`X 以外に ,恒等関数 `Y,`Z,`T 変数クラス・インスタンスを customize.py に定義することで多変数関数を扱えるようにしました。恒等関数 `X が引数タプルの 0 番目を取り出すのにたいし、`Y,`Z,`T は 引数タプルの 1 番目、2 番目 そして最後の要素を取り出させることで、多変数関数を扱えるようにしています。
(`X+`Y)(1,2,3) =============================== 3.0 sqrt(`X+`Y^2+`Z^2)(1,2,3) =============================== 3.74165738677 #数値計算による微分 ∂y(sqrt(`X+`Y^2+`Z^2))(1,2,3) =============================== 0.534522483688 # sympy による symbolic な微分の後に微分値を求める ts();float(∂y(ts.sqrt(`x+`y^2+`z^2)).subs([(`x,1),(`y,2),(`z,3)])) =============================== 0.534522483825
`X,`Y,`Z,`T のタプル引数の順番位置から値を抜き出す恒等関数を導入することで、数値関数でありながらもシンボリック処理に近い Python sf 式の記述が可能になることに注目願います。
kNumeric
kNumeric では微分・積分を中心とした頻繁に使われる数値演算を実装してあります。
kNumeric に実装してある微分は数値微分です。kNumeric に定義してある数値微分関数は P_(..) ですが、それを customize.py で受け直して ∂x, ∂y, ∂z, ∂t で微分できるようにしています。∂x, ∂y, ∂z, ∂t は、0 番目の引数, 一番目の引き数、二番目の引数、最後の引数についての微分を意味します。
∂x(sin)(0) =============================== 0.999999998333 ∂y(sin(`X+2`Y))(1,2) =============================== 0.567324367144 # sympy による symbolic な微分の後に微分値を求める ts();float(∂y(ts.sin(`x+2 `y)).subs([(`x,1),(`y,2),(`z,3)])) =============================== 0.567324370926 #複素数値微分 ∂x(exp)(1+2j) =============================== (-1.13120438564+2.47172667613j)
微分・積分については書くことが多すぎるので、別に章を改めて■ 微分,■ 積分でシンボリックな微分・積分も含めて説明します。
nearlyEq(..) 関数は浮動小数点値を変数、シーケンス・データ、行列、ベクタが相対的に 6 桁まで一致するとき True を返します。
浮動小数点値の数値計算には誤差がつき物です。理論的・理想的には等式が成り立っても、数値計算では非常に近い値になるだけで、等式が成り立たないことが頻繁に発生します。ですから 浮動小数点値は等しいことを == 演算子を使って比較しても、理論的には True であるが、浮動小数点値が僅かに異なるため、その結果が False になることが頻繁に発生します。このとき nearlyEq(..) を使うことで、浮動小数点変数、シーケンス・データ、行列、ベクタが殆ど同じ値であることを調べられます。
nearlyEq(3, 3.0000000001) =============================== True nearlyEq(3, 3.01) =============================== False nearlyEq(~[3,4], [3.0000000001, 4]) =============================== True nearlyEq( [3,4], [3.0000000001, 4]) =============================== True nearlyEq( [3,4], [3.01 , 4]) =============================== False nearlyEq(`σx,~[[1e-7,1],[1+1e-7,0]]) =============================== True nearlyEq(`σx,~[[1e-5,1],[1+1e-5,0]]) =============================== False
六桁の精度で一致するということは、殆ど同じであることを意味します。計算結果がランダムに分布するとしたら 100万回に一回の事象にに出くわしたことを意味します。そのような事象は単なる偶然ではなく、必然と思っても許されることが多いでしょう。
fft, ifft
FFT によるフーリエ変換は多くの分野で使われます。
vsGraph
vsGraph は 二次元グラフ表示関数:plotGr(..), 二次元/三次元の軌跡表示関数:plotTrajectory(..)、三次元グラフ表示関数:plot3dGr(..),タイムチャート表示関数:plotTmCh(..) などのデータ表示のための関数を実装してあります。
これらは Python sf のワン・ライナーでも扱いやすいように、最小の手間で最大の情報を表示させるように実装されています。最小の手間、論文などの赤の他人に読ませるための凡例など多くの情報をちりばめたグラフを作成するためには、pylab などのグラフ表示パッケージを使うべきです。
plotGr
最も多用されるグラフ表示は一変数関数の 2D 表示関数:plotGr(..) でしょう。とりあえずは「plotGr(関数, 開始位置:デフォルト0、終了位置:デフォルト1)」と「plotGr(シーケンス・データ)」の二つのグラフ表示方法を使い分けることにしておけば良いでしょう。
# デフォルト [0,1] 区間の sin 関数をグラフ表示 plotGr(sin)
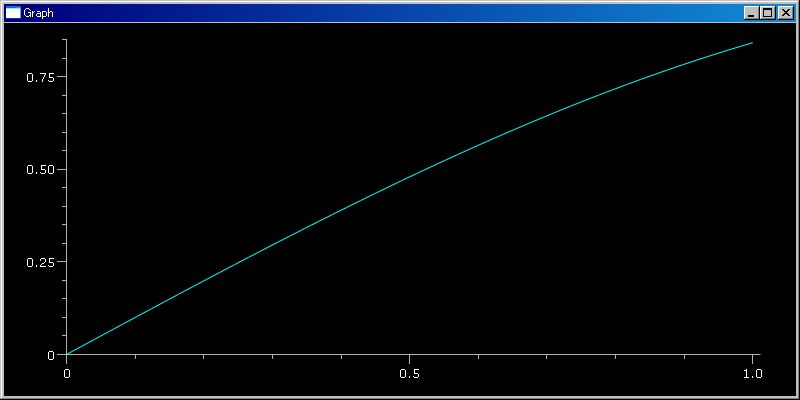
グラフ表示区間の開始位置、終了位置の数値引数を追加してやれば、その区間のグラフ表示をします。
# デフォルト [0,1] 区間の sin 関数をグラフ表示 plotGr(sin, -pi, pi)
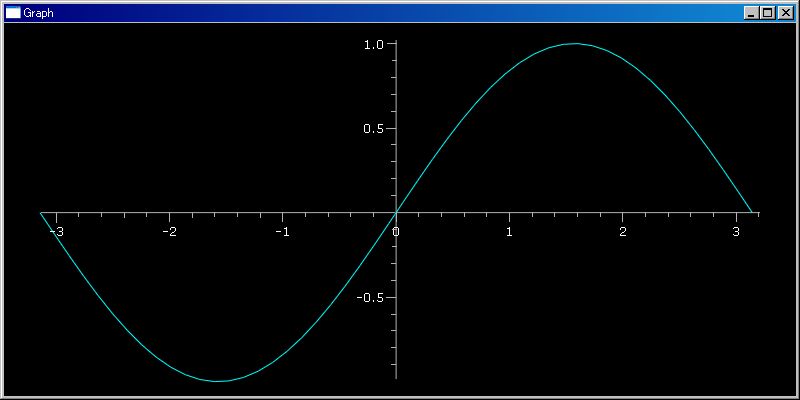
color キーワード引数を使うことで、グラフの線の色を指定できること、plotGr(..) 関数を複数回呼び出すことでグラフの重ね書きができることを覚えておくと便利です。
plotGr(`X^2);plotGr(`X^3,color=orange);plotGr(`X^5,0.5,0.9,color=green)
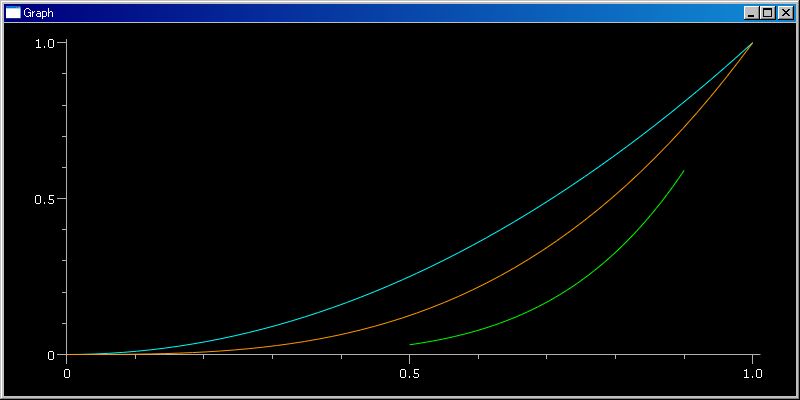
plotTrajectory
plotTrajectory(..) 関数は二次元または三次元での軌跡を描きます。
二つの要素からなるシーケンス・データ、例えば [(1,2), (3,4),..] のデータを引数として与えれば、(1,2), (3,4), ... 位置を直線で結んだ二次元の軌跡を描きます。軌跡の開始位置に |><| 記号が軌跡データの開始位置を示します
plotTrajectory([(1,2),(3,4),(-1,4)])
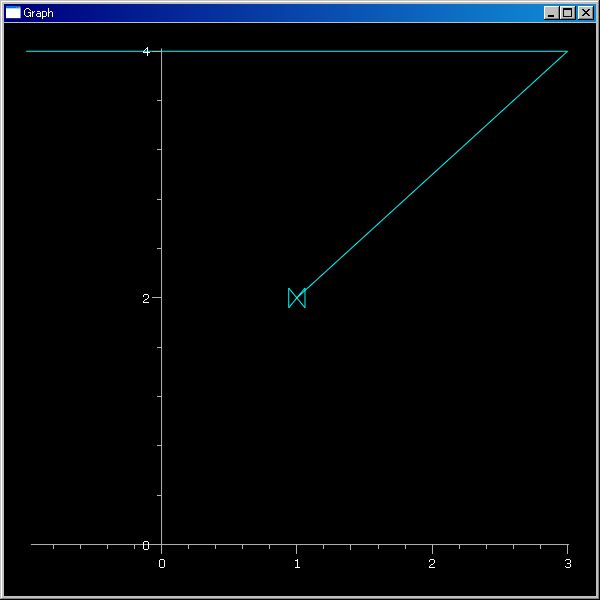
plotGr(..) と同様に、重ね書きもできます。、color 引数で軌跡の色を指定することもできです
f=plotTrajectory;f([(cos(x),sin(x)) for x in arsq(0,50,2pi/50)]);f([(0.5cos(2x),sin(3x)) for x in klsp(0,2pi)],color=orange)
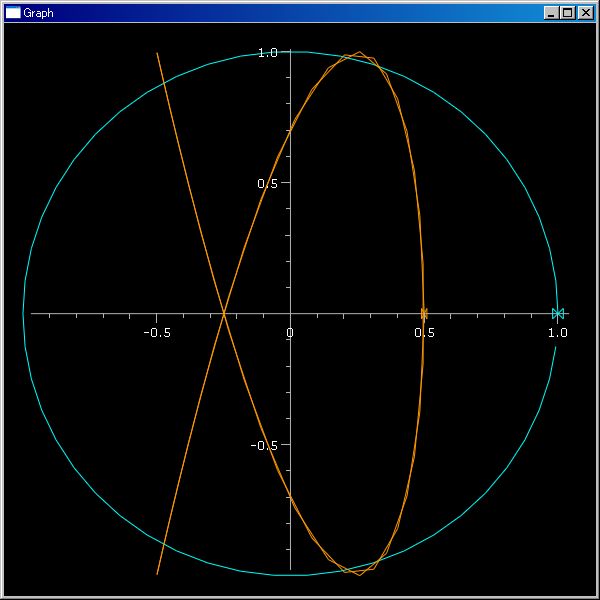
[(1,2,3),(4,5,6),...] のような三つ要素からなシーケンスのシーケンス・データを plotTrajectory(..) 引数に与えれば、それら三つ要素に対応する三次元で空間位置を直線で結んだ軌跡を描きます。球により軌跡の開始位置を示します。
plotTrajectory([(cos(x),sin(x),0.03x) for x in klsp(0,4pi)])
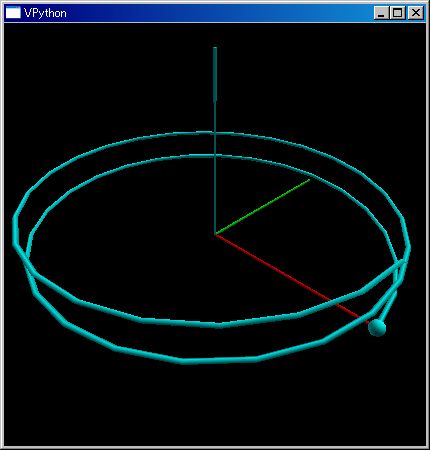
plot3dGr
plotGr(..) にシーケンス・データを与えてやれば、その与えられた点を直線で結んだ折れ線グラフを表示します。50 点以上のデータを与えてやれば、ディスプレー上では折れ線ではなく連続しているように見えるようになります。ただし、このとき横軸はシーケンス・データのインデックス整数値になります。シーケンス・データとしては lit, tuple, sc.ndarray ベクトル, ClTensor ベクトル何れでもグラフを表示します。
# デフォルト [0,1] 区間の sin 関数をグラフ表示 plotGr([0V`, 1V`, 1.5V`, 1.75V`, 1.9V`])
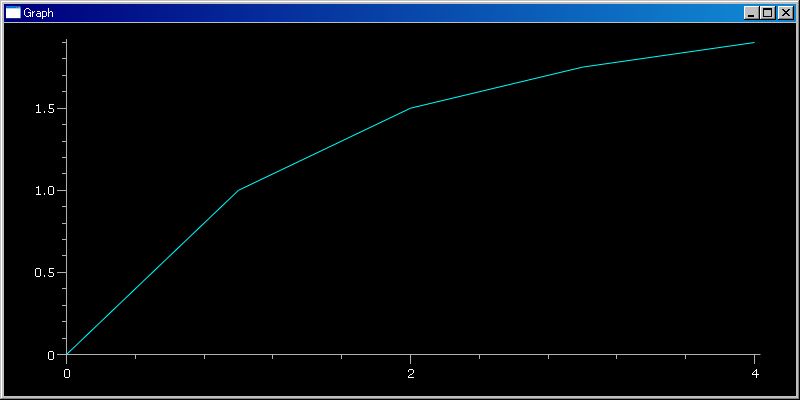
plot3dGr(..) は二次元平面上に分布する関数を 3D 表示します。
#(x^2-3xy+y^2)/(3+x+y) のニ変数有理関数のグラフを三次元表示させる # 表示領域は x ∈ [-1,1], y ∈ [-1,1] の正方形領域 plot3dGr((`X^2- 3`X `Y + `Y^2)/(3+`X+`Y), [-1,1])
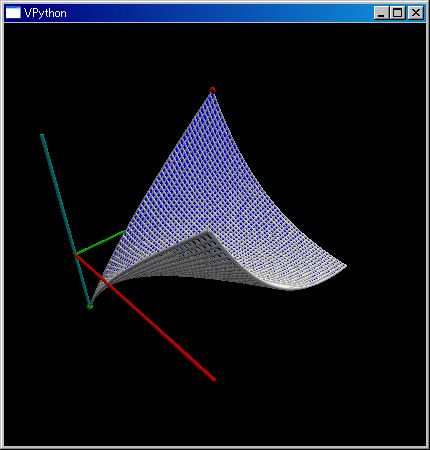
# # 表示領域は 実数∈ [-2,2], 虚数∈ [-2i,2i] の領域 plot3dGr((`X^2+`X+1)/(`X^2-1), [-2,2],[-2 `i, 2 `i])
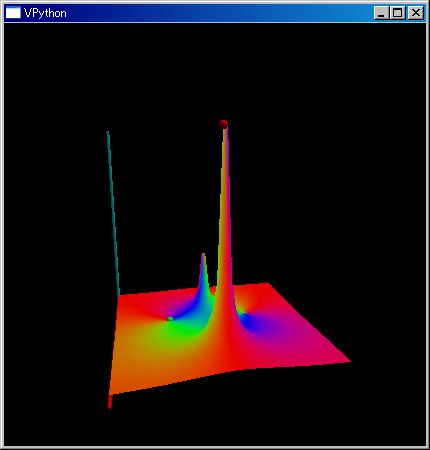
plotTmCh
plotTmCh(..) 関数に横長の行列データを与えることで、複数データのタイムチャート表示が可能です。
lst=range(32);plotTmCh(~[ [ 0.75^n sin(n pi/6) for n in lst], lst, lst[::-1], [0,1]*16])
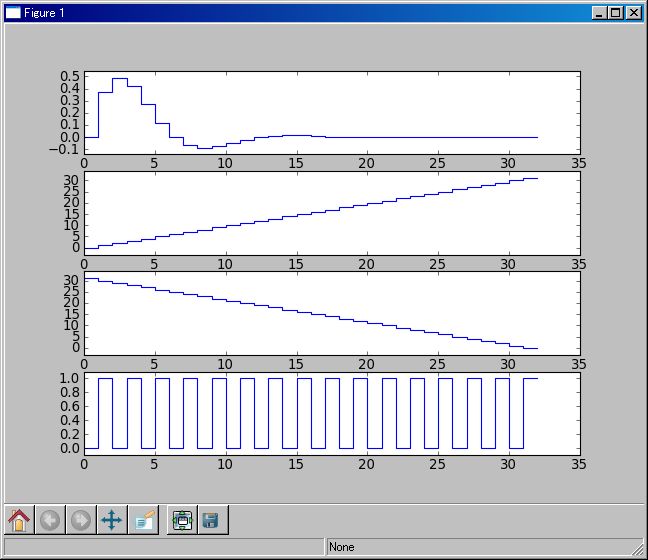
タイムチャート表示は、行列だけでなくベクトルにも使えます。ですから簡易ヒストグラム表示にも plotTmCh(..) が使えます。
plotTmCh([ 0.75^n sin(n pi/6) for n in range(32)])
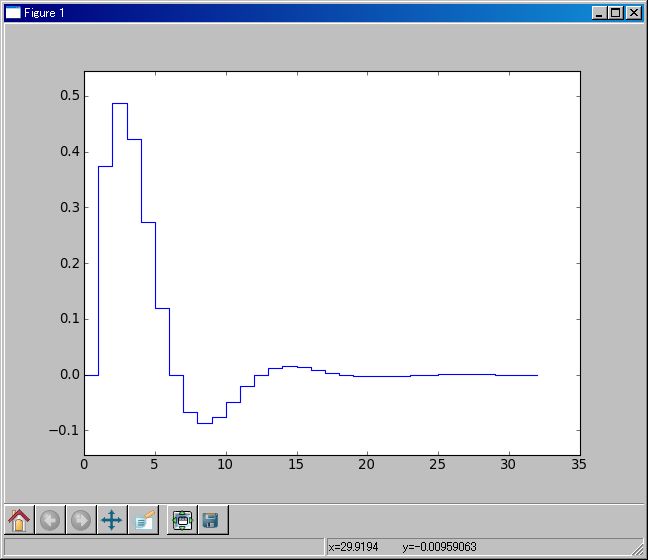
help(plotTrajectory) sc.source(plotTrajectory)
vsGraph.py ソース・コードも公開されています。それらを見てもらえば、ユーザーが望むグラフ表示関数を作ることも容易であることを分かってもらえると思います。一方で、グラフ表示への要望も千差万別です。ユーザーの専門分野によっても必要なグラフが異なってきます。御自分に必要なグラフ・ルーチンの修正・作成に是非ともチャレンジしてみてください。
rational
rational モジュールに実装してある ClRtnl クラスは、線形システムを記述するための有理関数を記述するクラスです。「ClRtnl(分子多項式係数リスト、分母多項式)」でインスタンスを生成します。
ClRtnl([1,2], [4,5,6]) =============================== 0.25 s + 0.5 ---------------- 2 s + 1.25 s + 1.5 cl=ClRtnl([1,2],[4,5,6]);cl.m_plNumer =============================== 0.25 s + 0.5 cl=ClRtnl([1,2],[4,5,6]);cl.m_plDenom =============================== 2 1 s + 1.25 s + 1.5
# pole cl=ClRtnl([1,2],[4,5,6]);cl.m_plDenom.roots =============================== [-0.625+1.05326872j -0.625-1.05326872j]
Laplace変換の s すなわち微分演算子相当の有理式に `s を割り当てています。`s についた加減乗除べき乗算の組み合わせ演算が可能です。それを利用して `s 分母多項式/`s 分子多項式の形式で ClRtnl で有理式を記述できます。
(`s+2)/(4`s^2+5`s+6)
===============================
0.25 s + 0.5
----------------
2
s + 1.25 s + 1.5
type((`s+2)/(4`s^2+5`s+6))
===============================
<class 'pysf.rational.ClRtnl'>
(`s+2)/(4`s^2+5`s+6) +1/(`s+1)
===============================
2
1.25 s + 2 s + 2
------------------------
3 2
s + 2.25 s + 2.75 s + 1.5
((`s+2)/(4`s^2+5`s+6)).m_plDenom
===============================
2
1 s + 1.25 s + 1.5
((`s+2)/(4`s^2+5`s+6) +1/(`s+1)).m_plDenom
===============================
3 2
1 s + 2.25 s + 2.75 s + 1.5
((`s+2)/(4`s^2+5`s+6) +1/(`s+1)).m_plNumer.roots
===============================
[-0.8+0.9797959j -0.8-0.9797959j]
ClRtnl 有理関数は関数の性質を持ち、与えられた実数引数に対して戻り値を持ちます
g=(`s+2)/(4`s^2+5`s+6) +1/(`s+1); [g(x) for x in range(3)] =============================== [1.3333333333333333, 0.69999999999999996, 0.45833333333333331]ClRtnl 有理関数、複素数引数に対しても戻り値を返します。
g=(`s+2)/(4`s^2+5`s+6) +1/(`s+1); [g(2pi `i f) for f in range(3)] =============================== [(1.3333333333333333+0j), (0.020281648531373049-0.19749798811716315j), (0.0051249180678231698-0.099279144279575723j)] g=(`s+2)/(4`s^2+5`s+6) +1/(`s+1);plot3dGr(g,[-1.5,-0.5],[-2`i,2`i])
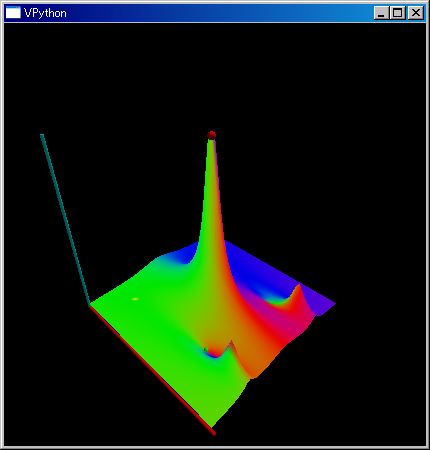
線形システムのために実装した有理関数ですから、ボード線図、インパルス応答、インディシャル応答、入力信号に対する応答出力を表すメソッドを備えています。
# Bode Plot ((`s+2)/(4`s^2+5`s+6) +1/(`s+1)).plotBode(0.01Hz`, 100 Hz`)
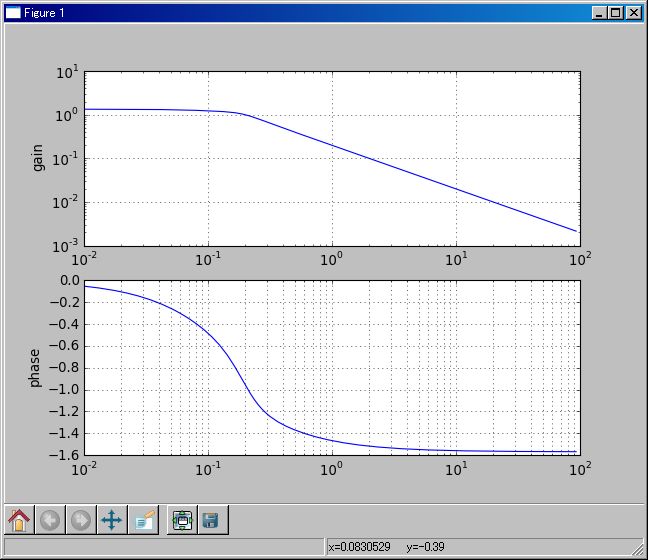
注意
(`s の多項式)(..) と書くと .. 部分は (`s の多項式)関数 の引数になってしまいます。.. 部分が多項式であってもです。(`s の多項式)*(..) の意味にはなりません。
# (`s+1)(`s+2) は (`s+2) を引数とする関数値です # (`s+1)(`s+2) == ((`s+2)+1) == `s+ (`s+1)(`s+2) == (`s+3) =============================== True (`s+1) (`s+2) =============================== 2 1 s + 3 s + 2 (`s+1)*(`s+2) =============================== 2 1 s + 3 s + 2
1/多項式left 多項式right は 多項式right/多項式left の意味です。1/多項式left 多項式right == (1/多項式left) 多項式right だからです。1/( 多項式left 多項式right) の意味ではありません。
1/(`s+1)(`s+2) == 1/(`s+3) =============================== True # 1/(`s+1) (`s+2) == (1/(`s+1)) (`s+2) == (`s+2)/(`s+1) 1/(`s+1) (`s+2) == (`s+2)/(`s+1) =============================== True =============================== True 1/((`s+1) (`s+2)) == 1/(`s^2+3`s+2) 1/((`s+1) (`s+2)) + 1/((`s+2) (`s+3))
コンデンサ 抵抗回路
ClRtnl 有理関数のインスタンスを作れれば、そのインパルス応答、インディシャル応答、任意の入力に対する応答を計算できます。下の単純な R C 一次遅れで、具体的に見ていきましょう。
1kΩ
────────MWMWMWMW──┬──────
↑ │ ↑
│ 10kHz sin wave ─┴─ 1uF │
Vin ─┬─ Vout
↓ │ ↓
──────────────┴──────
コンデンサのインピーダンスは 1/(C s) です。ですから、Vout/Vin 伝達関数は下のようになります。
#Vin/Vout 伝達関数 R,C=1kΩ`,1uF`;(1/(C `s)) / (R+1/(C `s)) =============================== 1000 -------- s + 1000
この Bode 線図は下のようになります
一例を見てみましょう。so サブ・パッケージの brentq(..) 関数は f(x)==0 となる x を brent 法で求めます。これを使えば逆関数を簡単に作れます。実際に Python sf には、これを使った逆関数を返す invF(..) を組み込んであります。下のような一行で済む単純なコードです。
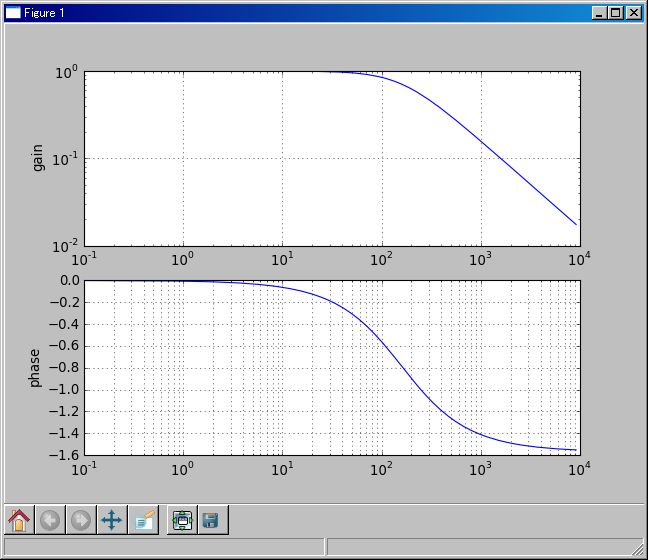
この回路の inpulse 応答は次のようになります。
R,C=1kΩ`,1uF`;Gs=(1/(C `s)) / (R+1/(C `s)); plotGr(Gs.getAnImpls(10ms`))
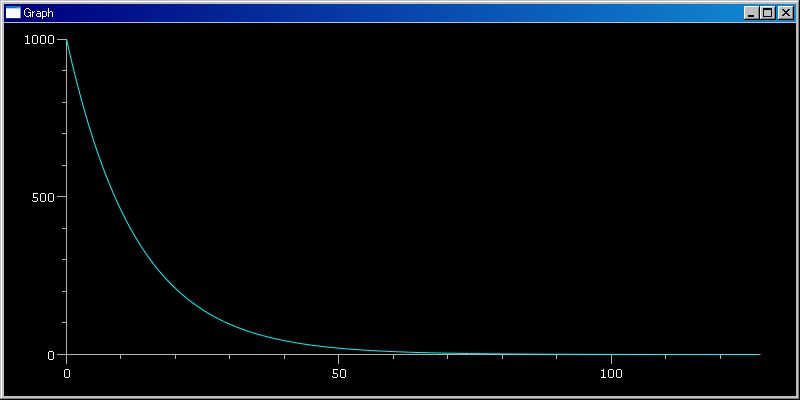
この回路の inditial 応答は次のようになります。
R,C=1kΩ`,1uF`;Gs=(1/(C `s)) / (R+1/(C `s)); Gs.plotAnRspns(10ms`)
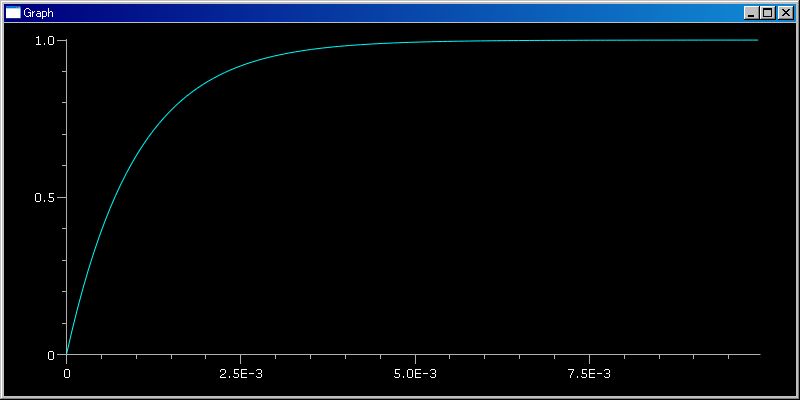
この回路に sin(2pi 10k` Hz) を入力したときの応答は次のようになります。
Δt=3ms`;R,C=1kΩ`,1uF`;Gs=(1/(C `s)) / (R+1/(C `s)); Gs.plotAnRspns(Δt, [sin(2pi 10k` Hz` t) for t in arsq(0,256,Δt/512)]);plotGr(0.03 sin(2pi 10k` Hz` `T), 0, 3ms`, N=512,color=orange)`s は加減乗除べき乗算ができるという意味では `X に似ています。でも `X の有理関数ではボード線図やインディシャル応答を計算する関数を持っていません。御注意ください。
■ scipy, sympy, visual, mayavi.mlab パッケージの動的な組み込み
sfFnctns.py は次に述べる scipy, sympy package を動的に import するための sy(),ts() 関数も備えています
scipy, sympy, visual, mayavi は、Python sf で無条件に取り込むには大規模すぎるパッケージです。それら全部取り込むと何秒もの時間を消費してしまいます。でも、これらは計算処理のためには有用であり、Python sf から簡単にアクセスできるようにすることも必要です。そのため sy, ts, mlb のパッケージ別名を、sy(), ts(),vs(), mlb() の関数を実行したときに、即ち それらが必要になったときに限って、それら個別のパッケージの別名をグローバル名前空間に取り込むようにしています。
sy():scipy パッケージの組み込み
sy() 関数を実行すると sy サブ名前空間に scipy package を取り込みます。scipy package は numpy package を包含する膨大な package です。scipy package の下に linalg, integrat,special,signal などのサブ・サプ名前空間を持ち、使い切れない有用な機能を実装しています。 でも sy サブ名前空間と sc 名前空間自体は非常に良く似ています。たとえば行列クラス sc.ndarray と sy.ndarray は全く同じものです。このことは 下のように identifier 番号が同じであることより確認できます。
sy();id(sy.ndarray) == id(sc.ndarray) =============================== True一方で numpy の sqrt,log は scipy の sqrt,log と関数の動作の自体が異っています。numpy の sqrt(..),log(..) は -1 引数にたいして nan:not a number を返すのですが、scipy の sqrt(..) は i を返します。log(..) は pi `i を返します。
sc.sqrt(-1) =============================== nan sc.log(-1) =============================== nan sy();sy.sqrt(-1) =============================== 1j sy();sy.log(-1) =============================== 3.14159265359jsc, sy サブ名前空間の違いは微妙です。色々と使ってもらって慣れるしか使い分けの方法はなさそうです。sqrt,log の微妙な問題は Python sf の基本数値関数を使う分には覆い隠されています。次のソースのような対策をしてあったりします。
sc.source(kNumeric.__log) In file: D:\my\vc7\mtCm\pysf\kNumeric.py def __log(ag): if hasattr(ag,'__len__'): import scipy if isinstance(ag,sc.ndarray) and not isinstance(ag, sf.ClTensor): return scipy.log(ag) else: return sf.krry(scipy.log(ag)) elif (isinstance(ag, (int, float)) and ag < 0): return sc.log(complex(ag)) else: return sc.log(ag) =============================== Noneさらに上の __log を ClAF クラスでラップしてやることで、Python sf 基本数値関数との加減乗除べき乗に関数合成を可能にしています。log = sf.ClAF(__log)他の Python sf 基本数値関数も、基本的には numpy の exp, sin, cos, tan, sinh, cosh, tanh, arcsin, arccos, arctan, log10, sqrt も ClAF でラップして、一部、対策が入っています。この意味で Python sf 基本数値関数は numpy の exp, sin, cos, tan, sinh, cosh, tanh, arcsin, arccos, arctan, log,log10, sqrt とは厳密には少し異なります。scipy package の凄さは、scipy が含む分野ごとに機能をまとめた sub package たちにあります。下のような sub package を scipy は含んでいます。普通の研究者や技術者では、これらの一割も使いこなせないと思います。
sy(); sc.info(sy) SciPy: A scientific computing package for Python ================================================ Documentation is available in the docstrings and online at http://docs.scipy.org. Contents -------- SciPy imports all the functions from the NumPy namespace, and in addition provides: Subpackages ----------- :: odr --- Orthogonal Distance Regression [*] misc --- Various utilities that don't have another home. cluster --- Vector Quantization / Kmeans [*] fftpack --- Discrete Fourier Transform algorithms [*] io --- Data input and output [*] sparse.linalg.eigen.lobpcg --- Locally Optimal Block Preconditioned Conjugate Gradient Method (LOBPCG) [*] special --- Airy Functions [*] lib.blas --- Wrappers to BLAS library [*] sparse.linalg.eigen --- Sparse Eigenvalue Solvers [*] stats --- Statistical Functions [*] lib --- Python wrappers to external libraries [*] lib.lapack --- Wrappers to LAPACK library [*] maxentropy --- Routines for fitting maximum entropy models [*] integrate --- Integration routines [*] ndimage --- n-dimensional image package [*] linalg --- Linear algebra routines [*] spatial --- Spatial data structures and algorithms [*] interpolate --- Interpolation Tools [*] sparse.linalg --- Sparse Linear Algebra [*] sparse.linalg.dsolve.umfpack --- :Interface to the UMFPACK library: [*] sparse.linalg.dsolve --- Linear Solvers [*] optimize --- Optimization Tools [*] sparse.linalg.eigen.arpack --- Eigenvalue solver using iterative methods. [*] signal --- Signal Processing Tools [*] sparse --- Sparse Matrices [*] [*] - using a package requires explicit import Global symbols from subpackages ------------------------------- :: misc --> info, factorial, factorial2, factorialk, comb, who, lena, central_diff_weights, derivative, pade, source fftpack --> fft, fftn, fft2, ifft, ifft2, ifftn, fftshift, ifftshift, fftfreq stats --> find_repeats linalg.dsolve.umfpack --> UmfpackContext Utility tools ------------- :: test --- Run scipy unittests show_config --- Show scipy build configuration show_numpy_config --- Show numpy build configuration __version__ --- Scipy version string __numpy_version__ --- Numpy version string =============================== Noneこれらの sub package のうち使用頻度の高い以下のものについては sy() 関数呼び出しで、同時にグローバル名前空間に sub package alias name:so,si,sl,ss,sg として取り込んでいます。
- so optimize 特定の条件を満たす変数値を求める関数群
- si integrate 積分を行う関数群
- sl linalg 行列の線形処理を行う関数群
- ss specia 特殊関数群
- sg signal 線形システムを処理する関数群
各サブ・モジュールに備わっている機能は「 sy();sc.info(so などのモジュール名)」の Python sf 式で打ち出せます。
sy();sc.info(so) Optimization Tools ================== A collection of general-purpose optimization routines.:: fmin -- Nelder-Mead Simplex algorithm (uses only function calls) fmin_powell -- Powell's (modified) level set method (uses only function calls) fmin_cg -- Non-linear (Polak-Ribiere) conjugate gradient algorithm ・ ・ brentq -- quadratic interpolation Brent method ・ ・ anderson -- extended Anderson method, the same as the broyden_generalized, but added w_0^2*I to before taking inversion to improve the stability anderson2 -- the Anderson method, the same as anderson, but formulated differently Utility Functions:: line_search -- Return a step that satisfies the strong Wolfe conditions. check_grad -- Check the supplied derivative using finite difference techniques. =============================== None
sc.source(invF)
In file: D:\my\vc7\mtCm\pysf\basicFnctns.py
def invF(f, rangeLeft=-1,rangeRight=1):
"""' Return inversed function. Default range of value is [-1,1]
Cation! For inv(f)(x),
the sign(f(x)-rangeLeft) * sign(f(x)-rangeRight) must be -1
e.g.
invF(sin)(pi/6)
===============================
0.551069583099
invF(sin,-pi/2, pi/2)(0.1)
===============================
0.100167421161
'"""
return lambda x:so.brentq(lambda t:f(t)-x, rangeLeft, rangeRight)
so optimize, si integrate, sl linalg, ss specia, sg signal には、数え切れないほどの有用な機能が詰め込まれています。sc.info(..) で、それらの機能を一度は見ておくことを薦めます。
scipy の全部を説明するなんて真似はできませんが、その主だった機能を■■ scipyの章に説明します。
ts():sympy パッケージの組み込み
sympy パッケージはシンボリックな計算処理を可能にするパッケージです。ts() 関数を呼び出すことで、sympy パッケージを ts の alias 名にしてグローバル名前空間に取り込みます。
sympy パッケージの読み込みに N280 CPU:ネットブック程度のパソコンでは 0.5 秒程度かかってしまいます。この動作遅れを嫌い、 sympy パッケージを使うときに限って、ts() を呼び出すことで sympy パッケージをダイナミックに import します。
ts() を呼び出すと、即ち sympy を import すると、ts の下の名前空間で、さまざまのシンボリックな計算が可能になります。
ts() を実行したとき、import sypy をするほかに、`x,`y,`z,`t,`p,`q,`n_ を sympy のシンボリックな変数として定義し ts サブ名前空間に取り込んでいます。ts() を呼び出した後は Python sf 式で、これらのシンボリック変数を定義済みとして扱えるようになります。を下のような具合です。
ts();((`x+1)^5).expand() =============================== 1 + 5*x + 10*x**2 + 10*x**3 + 5*x**4 + x**5 ts();((`x+`y)^3).expand() =============================== 3*x*y**2 + 3*y*x**2 + x**3 + y**3 #シンボリック微分 ts();ts.diff(ts.cos(`x^2),`x) =============================== -2*x*sin(x**2)ts() を実行すると、∂x,∂y,∂z,∂t,∂p,∂q は sympy 式についてはシンボリックな微分を、数値関数については数値微分を行うようになります。これらは ts() を呼び出さないと数値微分だけしか行えません。
∂x((`X+1)^2)(2) =============================== 5.99999999999 ts();∂x((`x+1)^2) =============================== 2 + 2*x ts();∂x((`x+1)^2).subs(`x,2) =============================== 6 ts();∂y(ts.sin(`x+`y+1)^2) =============================== 2*cos(1 + x + y)*sin(1 + x + y)ts() の実行により、物理単位付の計算も可能になります。
ts();R,C = 10.0kΩ`, 1uF`; R C =============================== 0.01*s`
その他、次のようなシンボリックな計算が ts()呼び出しの後に実行できます。
# 整数関連 有理数計算
ts();[`1r/k for k in range(8)]
===============================
[oo, 1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7]
ts();[`1r/k^2 for k in range(1,10)]
===============================
[1, 1/4, 1/9, 1/16, 1/25, 1/36, 1/49, 1/64, 1/81]
ts();sum([`1r/k^2 for k in range(1,10)])
===============================
9778141/6350400
# 整数を素数の積に分解する
ts();ts.factorint(2^12-1)
===============================
{3: 2, 13: 1, 5: 1, 7: 1}
# sympy 基本数値関数
ts();ts.sqrt(3)
===============================
3**(1/2)
# ts.I はシンボリックな虚数 i
ts();ts.sqrt(3+4 ts.I)
===============================
(3 + 4*I)**(1/2)
ts();ts.sqrt(3+4 ts.I)^2
===============================
3 + 4*I
# solve
# x + 5y - 2 == 0
# -3x + 6y - 15 == 0
ts();ts.solve([`x + 5`y - 2, -3`x + 6`y - 15], [`x, `y])
===============================
{x: -3, y: 1}
# solve for p,q
# x^2 == p^2+0.1q^2
# y^2 == 0.1p^2+q^2
ts();ts.solve([ts.Eq(`x^2,`p^2+0.1`q^2), ts.Eq(`y^2,`q^2+0.1`p^2)], [`p,`q])
===============================
[((1.01010101010101*x**2 - 0.101010101010101*y**2)**(1/2), (1.01010101010101*y**2 - 0.101010101010101*x**2)**(1/2)),
((1.01010101010101*x**2 - 0.101010101010101*y**2)**(1/2), -(1.01010101010101*y**2 - 0.101010101010101*x**2)**(1/2)),
(-(1.01010101010101*x**2 - 0.101010101010101*y**2)**(1/2), (1.01010101010101*y**2 - 0.101010101010101*x**2)**(1/2)),
(-(1.01010101010101*x**2 - 0.101010101010101*y**2)**(1/2), -(1.01010101010101*y**2 - 0.101010101010101*x**2)**(1/2))]
sympy の機能も膨大であり、その全部を説明するなんて真似はできませんが、その主だった機能を■■ scipyの章に説明します。
kmayavi:mlb
mayavi package の中に mlab sub package があります。pylab のようなグラフィックスに便利な関数・クラスが実装されています。有限要素法の計算結果を表示するような 3D グラフ表示に優れています。
ただし
-
mlab は発展途上であり、以下の問題があります。
- バージョンによって、細かい点で仕様が変わったりします。
- mgrid などを前提に作られており、使うのに大げさなものになりがちです。Python sf ワンライナーから呼び出せるような代物ではありません。
- マニュアルが分かりにくい。
- 動作が重い。N280 程度の CPU では 10 秒以上かかることが多い。
■ 単位付きの計算
PYthon sf では 電圧 V`, 電流 A`,抵抗 Ω`, 要領 uF` などの SI 単位系付きの演算・物理定数を扱えます。これらの単位系・物理定数が customize.py に定義してあるからです。
ただし、デフォルトでは V`, A`,Ω`, uF` の記号は使えますが、その値は単なる Python の float 値にすぎません。ts() を使って sympy を使えるようにすると、シンボリックな SI 単位付の sympy 値に変わります。
# 数値のみの単位系 C,R=2.2uF`,10kΩ`; C R =============================== 0.022 c` # light spped =============================== 299792458.0 100mile`/hour` =============================== 44.7027777778 # sympy 単位を持った、シンボリックな物理値 ts();C,R=2.2uF`,10kΩ`; C R =============================== 0.022*s` ts();c` # light spped ts();100mile`/hour` =============================== 44.7027777777778*m`/s`
どのような単位系、物理定数を使うかはユーザーごとに異なります。全てのユーザーを満足させる単位系・物理定数を記述することは無理です。配布した customize.py にある単位系・物理定数の設定を参考に、ユーザー自身が御自分に必要な単位・物理定数を編集ください。
シンボリックな単位系では、整数・有理数を保ちます
シンボリックな単位系では、加減乗除算の結果でも整数・有理数を保とうとします。計算結果として浮動小数点での数値が欲しいときは、物理量も「1. 単位」などと浮動小数点を指定してください。
ts(); 1 uH`/s` =============================== V`/(1000000*A`) ts(); 1. uH`/s` =============================== 1.0e-6*V`/A`
シンボリックな単位系付き値と Python sf 基本数値関数
Python sf 基本数値関数 exp, sin, cos, tan, sinh, cosh, tanh, arcsin, arccos, arctan, log, log10 の引数にシンボリックな単位付の値を与えるとき、その物理単位が打ち消しあっていないとエラーにしています。exp(..) などの引数に物理単位を持った値を入れて計算させても、その結果に物理的意味が無いからです。計算結果に設定すべき単位が定まらないからです。
ts();R,C = 10.0kΩ`, 1uF`; R C =============================== 0.01*s` ts();R,C = 10.0kΩ`, 1uF`; exp( 2 pi 10 Hz` R C ) =============================== 1.87445608759 ts();R,C = 10.0kΩ`, 1uF`; exp( R C ) AssertionError: At Float(.), you set physical quantity parameter,the units of which are not cancelled:0.01*s`
実は sympy の関数だと、exp(..) などに単位付の値を設定できて計算できてしまいます。
ts();R,C = 10.0kΩ`, 1uF`; ts.exp( R C ) =============================== exp(0.01*s`)
sqrt と `X,`Y,`Z,`T 恒等関数と その加減乗除べき乗についてはシンボリックな単位付の数値を受け付けます。その計算結果について物理単位を定められるからです。
ts();R,C = 10.0kΩ`, 1uF`; sqrt( R C ) =============================== 0.1*s`**(1/2) ts();L,C = 10.0 uH`, 1uF`; sqrt( L/C ) =============================== 3.16227766016838*V`/A` ts();m,v = 10.0 kg`, 2m`/s`; 1/2 m (`X^2)( v ) =============================== 20.0*m`**2*kg`/s`**2
シンボリックな単位系が望ましいとは限りません
一見 ts() を常に呼び出してシンボリックな単位系だけを使っておくべきに思えるでしょう。でも それが無理なときがあります。
典型的なのが伝達関数です。`s と物理値を組み合わせることができません。`s に 1/s`:[1/時間] の意味を与えられれば良いのでしょうが、現状の sympy と scipy を混在させる環境では、そのような ClRtnl クラスを作るのは至難の業です。ですから下のように ts() を呼び出さない、シンボリックな物理値ではなく、数値だけの物理係数値を使わねばなりません。plotBode(..) メソッドも sympy 単位付きの引数値を受け付けません。Python sf 基本数値関数は sympy 単位付きの引数値を受け付けますが、そのような Python コードにしてあるからです。Python 関数一般は sympy 単位付き引数値を受け付けません。
1kΩ`
────────MWMWMWMW──┬──────
↑ │ ↑
│ 10kHz sin wave ─┴─ 1uF │
Vin ─┬─ Vout
↓ │ ↓
──────────────┴──────
#Vin/Vout 伝達関数
R,C=1kΩ`,1uF`;(1/(C `s)) / (R+1/(C `s))
===============================
1000
--------
s + 1000
# Bode 線図
R,C=1kΩ`,1uF`;Gs=(1/(C `s)) / (R+1/(C `s)); Gs.plotBode(0.1Hz`,10k` Hz`)
MKSA+V 単位系
Python sf では sympy の SI 単位系を symIntf.py で定義し直しています。sympy にも単位系を定義してあるのですが、これは SI 単位系に沿った定義です。そして SI 単位系では、下のように抵抗が m**2*kg/(A**2*s**3) の単位になってしまうという不具合が付きまといます。Ωの単位がせめて V/A で表されれば通常のエンジニアにも理解可能ですが、m**2*kg/(2*s**3) の単位が抵抗の単位であると理解できる方は殆どいないでしょう。
ts();ts.ut.A import sympy.physics.units as ut;1 ut.V/(2 ut.A) =============================== m**2*kg/(2*A**2*s**3)
上のことは SI 単位系:MKSA 単位系が M:m:meter:長さ, K:kg:kilo gram:質量, S:s:sec:時間, A:A:ampere:電流を基本単位とする単位系だからです。抵抗:V/Aを MKSA の基本単位で表すと A がなくなって m**2*kg/(2*s**3) になってしまいます。
大多数のエンジニアは抵抗を V/A の単位で理解しています。m**2*kg/(2*s**3) の単位で理解していません。このことは、基本単位の組み合わせを MKSA ではなく MKSA + V で理解していることを意味します。(多くの方が このことを理解してくれません。如何でしょうか。)
Python sf では symIntf.py の中で MKSA と V を基本単位とする単位系に直しています。ですから、sympy.physics,units での単位系とは異なり、抵抗は V/A になります。電圧 V も基本単位とすると、それ以上の基本単位の組み合わせ分解できないからです。
ts(); 1 V`/ (2 A`) =============================== V`/(2*A`)ただし MKSA+V 単位系は冗長であることを意味します。電気での発生する単位時間当たりの熱量 W`:watt を単位時間あたり機械的熱量 J`/s` に交互に変換することはユーザーが行わねばなりません。
ts();1V` 2A` =============================== 2*A`*V` ts();1V` 2A` (J`/s`)/W` =============================== 2*m`**2*kg`/s`**3
抵抗を m**2*kg/(A**2*s**3) の単位で扱うことも誤りではありません。ただし殆どのエンジニアには通じないとも思います。それでも こちらの単位系を使いたい方は、customize.py を御自分で編集願います。sympy.physics,units を使って書き直すだけですから容易です。
tr()
sympy の計算をしているときでも、シンボリックな物理単位ではなく数値だけの物理単位を使うことを可能にしています。そのためには ts() 関数呼び出しの後に tr() 関数を呼び出します。
ts();R,C = 10.0kΩ`, 1uF`; ts.exp( R C ) =============================== exp(0.01*s`) ts();tr(); R,C = 10.0kΩ`, 1uF`; ts.exp( R C ) =============================== exp(0.01)
Float/Complex
物理単位付きの値や変数に加減乗除べき乗算を繰り返した結果、その物理単位が打ち消しあっているとき、その値を Float(..)/Complex(..) 関数によって Python の float/complex 値に変更できます。でも物理単位が消しあっていなときに Float(..)/Complex(..) 関数を使うとエラーになります。
ts();R,C = 10.0kΩ`, 1uF`; Float(2 s`/( R C)) =============================== 200.0 ts();R,C = 10.0kΩ`, 1uF`; Float( R C ) AssertionError: At Float(.), you set physical quantity parameter,the units of which are not cancelled:0.01*s`
Python sf 基本数値関数 exp, sin, cos, tan, sinh, cosh, tanh, arcsin, arccos, arctan, log, log10 の引数にシンボリックな単位付の値を与えるとき、その物理単位が打ち消しあっていないとエラーになるのは、Float/Complex を計算の途中で呼び出しているからです。
■ octn:oc
Python sf が用意している octn モジュールは Bool 体、八元数、8bit Galois 有元体, p元体 Zp, 一般体係数の多項式 Pl、有限群 Sn の代数系を定義しています。Python sf は octn モジュール内のクラスや関数を oc サブ名前空間の下で扱います。
後で述べる、任意の一般体要素からなる行列ベクトルを扱う ClFldTns と組み合わせて使うと、こんな少ない体だけでも様々の分野で強力な計算ツールとなります。
ClFldTns は任意の体、環を扱えます。ユーザーが自分で定義する代数系の多くを ClFldTns 行列クラスで扱えるはずです。そのとき octn.py モジュールが良い例になると思います。
Python sf の計算対象は Python sf で記述できるもの全てです。一般の数値計算だけとは限りません。群論や圏論さえ扱えます。そのような視点からも、以下の説明を読んでみてやってください。
oc.BF:Bool Field
Bool 体はデジタル回路など多くの分野で利用されます。そのため oc.BF ブール体を設けました。oc.BF のインスタンスは cusotomize.py で`1,`0 に割り振ってあります。
help(oc.BF)
class BF(__builtin__.object)
| ' Bool Field: meber is 1 or 0
| `1 * `0 = `0 # and
| `1 * `1 = `1
| `0 * `0 = `0
|
| `1 + `0 = `1 # xor
| `1 + `1 = `0
| `0 + `0 = `0
| '
・
・
`1,`0 は体であり、ClFldTns 行列クラスでの行列・ベクトル演算が可能です。
# oc.BF vector ~[`1,`0,`1] =============================== [1 0 1] ---- ClFldTns:---- # oc.BF add ~[`1,`0,`1] + ~[`0,`0,`1] =============================== [1 0 0] ---- ClFldTns: ---- # oc.BF 内積 ~[`1,`0,`1] ~[`0,`0,`1] =============================== 1 # oc.BF 行列 ~[[`1,`0,`1],[`0,`1,`1],[`0,`0,`1]] =============================== [[1 0 1] [0 1 1] [0 0 1]] ---- ClFldTns: ---- # oc.BF 逆行列 mt=~[[`1,`0,`1],[`0,`1,`1],[`0,`0,`1]];1/mt =============================== [[1 0 1] [0 1 1] [0 0 1]] ---- ClFldTns: ---- # oc.BF べき乗 mt=~[[`1,`0,`1],[`0,`1,`1],[`0,`0,`1]];mt^2 =============================== [[1 0 0] [0 1 0] [0 0 1]] ---- ClFldTns: ---- # oc.BF 行列 * vector mt,vc=~[[`1,`0,`1],[`0,`1,`1],[`0,`0,`1]], ~[`1,`0,`1]; mt vc =============================== [0 1 1] ---- ClFldTns: ----
oc.Oc:Octonion
非可換な代数系、また推移率さえ成り立たない代数系の例として八元数: ClOctonion を実装しました。cl.Oc の alias 名を持ちます。
help(oc.Oc)
Help on class ClOctonion in module pysf.octn:
class ClOctonion(__builtin__.object)
| ' Octonion class including quaternion, complex, and real numbers
| alias name Oc
| examples: assuming import octn as oc
| declaration of octernion
| oc.Oc([1,2,3,4,5,6,7,8])
| ===============================
| (1, 2, 3, 4, 5, 6, 7, 8)
|
| oc.Oc(1,2,3,4,5,6,7,8)
| ===============================
| (1, 2, 3, 4, 5, 6, 7, 8)
|
| declaration of quaternion
| oc.Oc([1,2,3,4])
| ===============================
| (1, 2, 3, 4)
|
| oc.Oc(1,2,3,4)
| ===============================
| (1, 2, 3, 4)
|
| declaration of complex number
| oc.Oc([1,2])
| ===============================
| (1, 2)
| oc.Oc(1,2)
| ===============================
| (1, 2)
|
| +-*/ ** operations: assuming a = a = oc.Oc(1,2,3,4,5,6,7,8); b = oc.Oc(1,2,3,4)
| a+b
| ===============================
| (2, 4, 6, 8, 5, 6, 7, 8)
|
| a-b
| ===============================
| (0, 0, 0, 0, 5, 6, 7, 8)
|
| a*b
| ===============================
| (-28, 4, 6, 8, 70, -8, 0, -16)
|
| a/b
| ===============================
| (1.0, 0.0, 0.0, -2.7755575615628914e-017, -2.0, 0.66666666666666674, 0.46666666666666662, 1.0666666666666667)
|
| a**3 # power is defined only for integer
| ===============================
| (-272, -148, -768, -1052, -328, -1788, -896, -2020)
|
| a**-3
| ===============================
| (-0.64705882352941146, 0.76470588235294079, 3.8235294117647052, 4.4117647058823533, 1.7058823529411766, 8.882352941176471, 4.5294117647058822, 10.058823529411764)
|
・
・
八元体の部分体として Quaternion を持つことにもなります。oc.Oc(1,3,5,7) など四つの要素からなるときが四元数部分体になるように作ってあります。
O=oc.Oc;O(0,1,0,0) O(0,1,0,0) =============================== -1 O=oc.Oc;O(0,1,0,0) O(0,0,1,0) =============================== (0, 0, 0, 1)
非可換体では逆行列が意味を持ちません。でも L U 分解アルゴリズムは非可換体要素の行列でも動作してしまいます。逆行列を計算してしまいます。ですから、非可換体で行列と その逆行列積が単位行列にならないことを数値実験で確認できます。
O=oc.Oc;mt=~[[O(0,1,2),O(1,2,3)],[O(2,3,4),O(9)]] =============================== [[(0, 1, 2, 0) (1, 2, 3, 0)] [(2, 3, 4, 0) 9]] ---- ClFldTns:---- O=oc.Oc;mt=~[[O(0,1,2),O(1,2,3)],[O(2,3,4),O(9)]]; mt/mt =============================== [[(1.0, -0.4642461538461537, 0.23212307692307688, 0.71384615384615402) (-5.5511151231257827e-17, 0.11076923076923073, -0.055384615384615365, -0.17230769230769227)] [ (0.28553846153846152, -1.3887999999999998, 0.86670769230769229, 0.22646153846153888) (0.93107692307692291, 0.3593846153846153, -0.23507692307692296, -0.2683076923076923)]] ---- ClFldTns: ----
oc.Pl: 任意体係数の多項式
oc.Pl は任意の体係数にとれる多項式クラスです。
help(oc.Pl)
class Pl(__builtin__.object)
| ' polynomial for algebraic coefficients
| Implemented 'has a relation' with scipy.poly1d
| At matrix operations, it may cause unexpected operations to inherit
| scipy.poly1d. Because poly1d is implemented under assumption of int
| float coefficients.
|
| e.g.
| import octn as oc
| oc.Pl(1,2,3,4) # a integer coefficient polynomial
| =============================== # int type is estimated from paramters
| 1x^3+2x^2+3x+4
|
| lst=[1,2,3,4];oc.Pl(lst) # can use sequence argment too
| ===============================
| 1x^3+2x^2+3x+4
|
| oc.Pl(1,2,3,4, variable='D') # assign polynomial variable string
| ===============================
| 1D^3+2D^2+3D+4
|
| oc.Pl(1,2,3,4, oc.BF) # assgin bool field coefficient
| ===============================
| x^3+x # 0 suppressed
|
| oc.Pl(1,2,3,4, dtype=oc.BF) # assgin bool field coefficient 2
| ===============================
| x^3+x
|
| oc.Pl(1,2,3,`1) # assign type estimating from argments
| =============================== # ;;type(sum([1,2,3,`1])) #== oc.BF
| x^3+x+1
・
・
この一般多項式は加減乗除べき乗算が可能です。一般多項式の割り算は 商と余りのペアを返します。有理関数ではありません。
oc.Pl(1,2,3,4)+oc.Pl(5,6,7,8) =============================== 6x^3+8x^2+10x+12 oc.Pl(1,2,3,4) oc.Pl(5,6,7,8) =============================== 5x^6+16x^5+34x^4+60x^3+61x^2+52x+32 oc.Pl(1,2,3,4)^2 =============================== 1x^6+4x^5+10x^4+20x^3+25x^2+24x+16 oc.Pl(1,2,3,4)/oc.Pl(5,6,7,8) =============================== (Pl(0), Pl(1x^3+2x^2+3x+4))
一般体多項式での割り算は、代数系の拡張で頻繁に使われます。下のように GF(2^8) Galois 有元体での積演算を計算できます。
oc.Pl([1, 0,0,0,1, 1,1,0,1], oc.BF) =============================== x^8+x^4+x^3+x^2+1 oc.Pl([1,1,0,0, 0,0,0,1], oc.BF) oc.Pl([0,1,1,0, 0,0,0,1], oc.BF)/oc.Pl([1, 0,0,0,1, 1,1,0,1], oc.BF) =============================== (Pl(x^5+x^3+x+1), Pl(x^7+x^6+x^3+x^2+x))
oc.RS: Galois 有元体
x^8 + x^4 + x^3 + x^2 + 1 を primitive polynomial とする Galois 有元体を定義してあります。CD や DVD フォーマットで使われている有元体です。
help(oc.RS)
Help on class RS in module pysf.octn:
class RS(__builtin__.object)
| ' GF(2^8) for primitive polynomial:x^8 + x^4 + x^3 + x^2 + 1:0x1d
| RS.m_lstPwrStt has power values
| e.g;; oc.RS.m_lstPwrStt
| [1, 2, 4, 8, 16, 32, 64, 128, 29, 58, ... 173, 71, 142]
|
| oc.RS(24) oc.RS(31)
| ===============================
| 0x15
|
| oc.RS.m_lstPwrStt.index(24)
| ===============================
| 28
|
| oc.RS.m_lstPwrStt.index(31)
| ===============================
| 113
|
| hex(oc.RS.m_lstPwrStt[28+113])
| ===============================
| 0x15
・
・
ClFldTns は oc.RS Galois 有元体を要素とする行列演算が可能であり Reed Solomon エラー訂正コードなどの数値実験が可能です。
α=oc.RS(2);gx=oc.Pl(1,α^0) oc.Pl(1,α) oc.Pl(1,α^2) oc.Pl(1,α^3) =============================== 0x01x^4+0x0fx^3+0x36x^2+0x78x+0x40 α=oc.RS(2);gx=oc.Pl(1,α^0) oc.Pl(1,α) oc.Pl(1,α^2) oc.Pl(1,α^3); gx(1) =============================== 0x00 mt=~[ [1,2],[3,4], oc.RS]; 1/mt =============================== [[0x02 0x01] [0x8f 0x8e]] ---- ClFldTns:---- mt=~[ [1,2],[3,4], oc.RS]; mt/mt =============================== [[0x01 0x00] [0x00 0x01]] ---- ClFldTns: ---- mt=~[ [1,2],[3,4], oc.RS]; mt^-1 [3,4] =============================== [0x02 0x8e] ---- ClFldTns: ----
oc.Zp: p 元体
passoc.Sn: n 次置換群
pass■ tlRcGn:tn
tlRnGn モジュールは無限繰り返し処理関連の機能を実装してあります。特に無限数列についての実装が実用的なレベルにあると思います。tn のサブ名前空間の下に これを置きます。
Python は関数の第一級のオブジェクトであり、関数プログラミングに近い記述が可能です。そして itertools モジュールで無限解の繰り返しに関連するコードが実装されています。
ただし itertools は繰り返しのためのジェネレータが実装されているのであり、無限数数列を扱うためには実装されていません。特に intertools で定義されているクラスには __getitem(..) method が定義されていません。sequence[idx] or sequence[idxS:idxE] のような記述ができません。それを可能にする tn.cout, tn.imap, tn.cycle, tn.repeat, tn.izip, tn.ifilter, tn.ifilterfalse, tn.islice, tn.startmap, tn.chain, tn.takewhile, tn.dropwhile, tn.groupby, tn.mix を設けました。
■ Python sf 基本数値関数
`X,`Y,`Z,`Texp, sin, cos, tan, sinh, cosh, tanh, arcsin, arccos, arctan, log, log10, sqrt と `X,`Y,`Z,`Tは「Python sf 基本数値関数」と名づけている特別な関数です。
これらは numpy の関数を継承してあるので、複素数値引数も計算可能です。ですから、下のように arctan(..) 関数の分布の様子を複素平面上で複素位相含めて、簡単に表示できます。
plot3dGr(arctan,[-pi,pi],[-pi `i, pi `i])
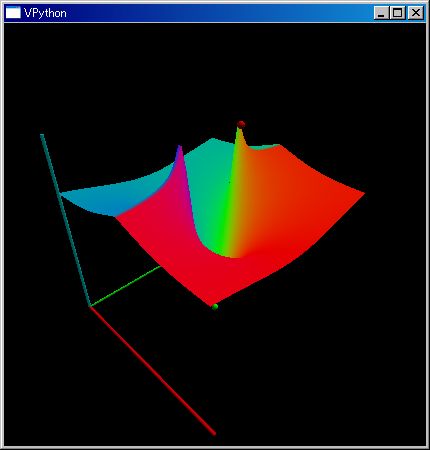
Python の math built in module の三角関数は、実数値引数しか計算できません。
import math;math.cos(pi/3) =============================== 0.5 import math;math.cos(pi/3+1j) can't convert complex to float at excecuting:math.cos(pi/3+1j) # Python sf 基本数値関数なので複素数値引数でも計算できます cos(pi/3+1j) =============================== (0.771540317408-1.01775408825j)
Python sf 基本数値関数は numpy 関数を継承しているので ufunc です。すなわちベクトルや行列引数を与えると、その要素たちの関数値を要素とする行列を返します。
sc.arange(4) =============================== [0 1 2 3] sc.arange(-4,4) =============================== [-4 -3 -2 -1 0 1 2 3] # ndarray 引数を与えると ndarray 値を返します sin(sc.arange(-4,4) pi/4) =============================== [ -1.22464680e-16 -7.07106781e-01 -1.00000000e+00 -7.07106781e-01 0.00000000e+00 7.07106781e-01 1.00000000e+00 7.07106781e-01] # ClTensor 引数を与えると ClTensor 値を返します sin(~[range(-4,4)] pi/4) =============================== [ -1.22464680e-16 -7.07106781e-01 -1.00000000e+00 -7.07106781e-01 0.00000000e+00 7.07106781e-01 1.00000000e+00 7.07106781e-01] ---- ClTensor ---- # 特殊関数:エラー関数:erf(..) も ufunc であり ClTensor 引数のとき ClTensor を返します sy();ss.erf(~[range(-4,4)] pi/4) =============================== [-0.99999112 -0.99913826 -0.97367893 -0.73331143 0. 0.73331143 0.97367893 0.99913826] ---- ClTensor ---- # Python sf 基本数値関数(行列引数) cos(`σx) =============================== [[ 1. 0.54030231] [ 0.54030231 1. ]] ---- ClTensor ----
list や tuple シーケンス・データを与えたとき、Python sf 基本数値関数は ClTensor ベクトルを返します。
(`X^2)( (1,2,3,4) ) =============================== [ 1. 4. 9. 16.] ---- ClTensor ---- arsq(0, 6, pi/3) =============================== (0.0, 1.0471975511965976, 2.0943951023931953, 3.1415926535897931, 4.1887902047863905, 5.2359877559829879) sin(arsq(0, 6, pi/3)) =============================== [ 0.00000000e+00 8.66025404e-01 8.66025404e-01 1.22464680e-16 -8.66025404e-01 -8.66025404e-01] ---- ClTensor ----
Python sf 基本数値関数については、関数のままで加減乗除べき乗算と関数の合成を可能にしています。ですから以下のような Python sf 式での計算が可能です。
#`X の多項式 (`X^2+ 2`X + 1)(2) =============================== 9.0 #`X の有理式の複素数値分布 plot3dGr( (`X-1)/(`X^2 + `X + 1), [-2,2],[-2`i, 2`i], True)
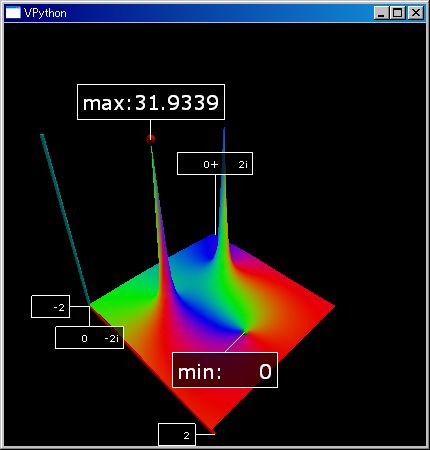
# 関数の積 f=(2 sin cos); f(pi/2) =============================== 1.22464679915e-16 # 関数の合成 plotGr(tan(cos),-2pi,2pi)
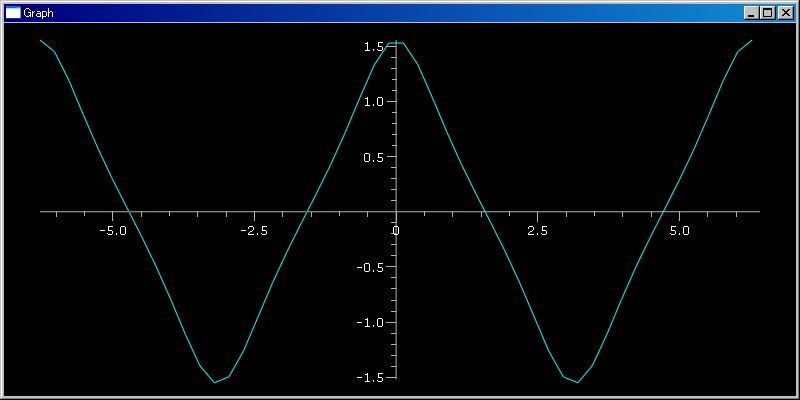
Python sf 基本数値関数に単位付の引数を与える
plotGr(sin cos, -pi, pi) plotGr(sin(`X^2), -pi, pi) 注意;; (`X^2)(3) ufunc と行列・ベクトル ベクトル・行列 要素に作用する 型を保つ `X(..) 関数の引数に与えられるのは int,float,complex のみ。BF:`1 や oc.RS(1) などは与えられない ← int,float,complex 係数の多項式を使って `X が実装されているから。 help(ClRtnl) 基本数値関数の加減乗除べき乗算と合成 sympy 単位付数値の計算
:=, =: 記号とファイル変数
ts() sc.info(sc) help(sc) sc.sinc(1) a,b,c=2,3,4; S=(a+b+c)/2;sqrt(S*(S-a)*(S-b)*(S-c)) # Heron's formula a,b,c=2,3,4; S=(a+b+c)/2;sqrt(S (S-a) (S-b) (S-c)) # Heron's formula =============================== 2.90473750966 a,b,c=1,2,3; ( -b + sqrt(b**2-4* a* c) )/(2*a) =============================== (-1+1.41421356237j) a,b,c=1,2,3; ( -b + sqrt(b^2-4 a c) )/(2a) =============================== (-1+1.41421356237j)sin(pi/3) を計算させるのに、Python では下の様に書かねばなりません。
//@@ import numpy as sc print sc.sin(sc.pi/3) //@@@ 0.866025403784
モジュールを何も import していない裸のPython には sin/cos などの基本数値関数を計算する機能は入っていません。scipy などのモジュールを import してやって、初めて sin,cos, exp, log,.. などの計算が可能になります。
「import numpy as sc」の一行は「numpy モジュールをインポートして sc の名前空間の下で扱えるようにする」ことを意味しています。sc.sin, sc.pi の名前によって、numpy モジュールに定義してある関数や変数値をアクセスしています。
でも計算ソフトとしては sin,cos,exp.. pi のような基本的な関数や定数を sc などの名前空間に閉じ込めておくべきではありません。計算の度に import numpy as sc の行を記述することも馬鹿げています。さらに言えば、計算させた最終値は人間が理解できる文字列として出力するのだから print 文さえ冗長です。
Python sf プリプロセッサは
- 使われる頻度の高い「import numpy as sc」は常に実行済みの状態にして
- sc.sin, sc.cos, sc.exp ..., sc.pi などの基本数値関数・定数は sin, cos, exp, ..., pi と「sc.」を取り去った関数名・定数名にして
- 最後の式の値については print 文を自動的に追加して
sin(pi/3) =============================== 0.866025403784
Python sf プリプロセッサは変数名・関数名を拡張します。Python 文法を超えた
Python の scipy モジュールには、科学計算のための膨大なクラス・関数が蓄積されています。膨大な Matlab の計算機能の八割ぐらいが蓄積済みと言えるともいます。 plotGr(∂x(sin + 2 cos(λ x:3 x)), -pi, pi) plotGr(sin + 2 cos(λ x:3 x), -pi, pi) 無理sc.source(~+) 1 ~+ 2 プリプロセッサ 演算子記号 import ModuleName as mn
tr();(`x+`y)^2 == `x^2 + 2 `x `y + `y^2 =============================== False tr();ts.expand((`x+`y)^2) == `x^2 + 2 `x `y + `y^2 =============================== Truets,sc,tn
■ 行列操作 II
sc.diag([1,2,3,4]) ~[sc.diag([1,2,3,4])] krry(sc.diag([1,2,3,4]))そのほかの行列ベクトルの主な機能
行列式,転置行列、複素共役転置行列、r
mt=`σx;mt.r[0]=100;`σx =============================== [[ 100. 1.] [ 1. 0.]] ---- ClTensor ---- conjugate transpose dogger r help(ClTensor)テンソルの index:[..] に tuple/list を与えたときで動作は異なります。口ではうまく説明で気なので、実際の動作を見てください
`εL
===============================
[[[ 0. 0. 0.]
[ 0. 0. 1.]
[ 0. -1. 0.]]
[[ 0. 0. -1.]
[ 0. 0. 0.]
[ 1. 0. 0.]]
[[ 0. 1. 0.]
[-1. 0. 0.]
[ 0. 0. 0.]]]
---- ClTensor ----
idx=[0,2,1];`εL[idx]
===============================
[[[ 0. 0. 0.]
[ 0. 0. 1.]
[ 0. -1. 0.]]
[[ 0. 1. 0.]
[-1. 0. 0.]
[ 0. 0. 0.]]
[[ 0. 0. -1.]
[ 0. 0. 0.]
[ 1. 0. 0.]]]
---- ClTensor ----
idx=(0,2,1);`εL[idx]
===============================
-1.0
idx=(0,2,1);`εL[*idx]
invalid syntax (, line 1) at excecuting:k__bq__sEpsilon_L___[*idx]
sc.ndarray についても、ClTensor と同様な動きです。
sc.array(`εL) =============================== [[[ 0. 0. 0.] [ 0. 0. 1.] [ 0. -1. 0.]] [[ 0. 0. -1.] [ 0. 0. 0.] [ 1. 0. 0.]] [[ 0. 1. 0.] [-1. 0. 0.] [ 0. 0. 0.]]] idx=[0,2,1];sc.array(`εL[idx]) =============================== [[[ 0. 0. 0.] [ 0. 0. 1.] [ 0. -1. 0.]] [[ 0. 1. 0.] [-1. 0. 0.] [ 0. 0. 0.]] [[ 0. 0. -1.] [ 0. 0. 0.] [ 1. 0. 0.]]] idx=(0,2,1);sc.array(`εL[idx]) =============================== -1.0 idx=(0,2,1);sc.array(`εL[*idx]) invalid syntax (m_dtrm .d .t .r, line 1) at excecuting:sc.array(k__bq__sEpsilon_L___[*idx])
固有値/固有ベクタ
scipy には普通の方が使う、行列に関する計算の殆どが既に備わっています。 sc.info(sc) 行列の固有値
H = `σx + `σy + `σz; eigvals(H)
H = `σx + `σy + `σz; eig(H)[1]
三階以上の tensor
(vector or matrix or tensor) ^ (vector or matrix or tensor)
■ ClFldTns 一般体を要素とする行列
scipy の行列・ベクトルは整数・実数・複素数を要素とする行列・ベクトルであり、Bool 体など、一般の体を要素とする行列は扱えません。厳密には要素を object タイプとして行列とすれば scipy でも任意の要素をもった行列を作れるのですが、加減乗除算に無理があります。とくに object タイプの行列では逆行列が計算できないのは致命的です。lapack を使って高速に逆行列を計算しているのですから当然ですが。
Python sf では、任意の体を要素とする行列を扱えます。そのために ClFldTns 行列クラスを実装しています。どんな体を要素とする行列であっても逆行列も計算できます。愚直に L R 分解アルゴリズムで逆行列を計算しています。ですから ユーザーが作った体クラスを要素とする ClFldTns 行列であっても、逆行列を計算できます。Duck typing で加減乗除を繰り返す L R 分解アルゴリズムを実行するだけです。
一般体でも ~[...] による行列やベクトルの生成を使えます。int, float, complex 以外の要素が入ってきたとき ClFldTns クラスのインスタンスにしています。`1,`0 Bool 体を要素とする行列を次のように作り また計算できます。
# Bool 体要素をベクトルとする行列の生成 ~[`1,`0,`1,`1] =============================== [1 0 1 1] ---- ClFldTns:---- # type 指定による ClFldTns ベクトルの生成 ~[1,0,1,1,1,1,0,0,1, oc.BF] =============================== [1 0 1 1 1 1 0 0 1] ---- ClFldTns: ---- # 和 ~[`1,`0,`1,`1] + ~[`1,`0,`0,`1] =============================== [0 0 1 0] ---- ClFldTns: ---- # 内積 ~[`1,`0,`1,`1] ~[`1,`0,`0,`1] =============================== 0 # Diadic 外積 ~[`1,`0,`1,`1] ^ ~[`1,`0,`0,`1] =============================== [[1 0 0 1] [0 0 0 0] [1 0 0 1] [1 0 0 1]] ---- ClFldTns: ---- # 行列の生成 ~[ [`0,`1],[`1,`0]] =============================== [[0 1] [1 0]] ---- ClFldTns: ---- # 行列とベクトルの積 ~[ [`0,`1],[`1,`0]] ~[`1,`0] =============================== [0 1] ---- ClFldTns: ---- # 行列のべき乗 ~[ [`0,`1],[`1,`0]]^3 =============================== [[0 1] [1 0]] ---- ClFldTns: ----
逆行列を使わないのならば、環の要素からなる行列やベクトルを作り、加減乗べき乗算も可能です。
# 多項式の生成 P=oc.Pl; P(1,2,3,4,5) =============================== 1x^4+2x^3+3x^2+4x+5 # 多項式ベクトルの生成 P=oc.Pl; ~[P([1,2,3]),P([4,5,6])] =============================== [1x^2+2x+3 4x^2+5x+6] ---- ClFldTns:関数を要素とする行列---- # 多項式ベクトルの引数値を与えて計算させる P=oc.Pl; ~[P([1,2,3]),P([4,5,6])](1) =============================== [ 6. 15.] ---- ClTensor ---- # 多項式行列の生成 P=oc.Pl; ~[ [P([1,2,3]),P([4,5,6])],[P([1,2]),P([4,5])] ] =============================== [[1x^2+2x+3 4x^2+5x+6] [1x+2 4x+5]] ---- ClFldTns: ---- # 多項式行列のべき乗 P=oc.Pl; ~[ [P([1,2,3]),P([4,5,6])],[P([1,2]),P([4,5])] ]^3 =============================== [[1x^6+14x^5+79x^4+224x^3+358x^2+326x+159 4x^6+53x^5+274x^4+692x^3+1006x^2+845x+366] [1x^5+14x^4+76x^3+194x^2+241x+122 4x^5+53x^4+262x^3+581x^2+628x+281]] ---- ClFldTns: ---- # 多項式行列の逆行列を計算させるのは無理です P=oc.Pl; ~[ [P([1,2,3]),P([4,5,6])],[P([1,2]),P([4,5])] ]^-1 int() argument must be a string or a number, not 'tuple' at excecuting:krry__(*[ [P([1,2,3]),P([4,5,6])],[P([1,2]),P([4,5])] ])**-1
python 基本数値関数: exp, sin, cos, tan, sinh, cosh, tanh, arcsin, arccos, arctan, log, log10, sqrt と `X,`Y,`Z,`T は加減乗除算が可能です。環になっています。ならば Python 基本数値関数と その組み合わせ関数を要素とする行列を作れます。
∂J(~[`X+`Y,`X^2+`Y^2+`Z^2, `X `Y `Z]) `div(~[`X+`Y,`X^2+`Y^2+`Z^2, `X `Y `Z]) `rot(~[`X+`Y,`X^2+`Y^2+`Z^2, `X `Y `Z])
加減乗除べき乗算が可能な norm 関数
■ 微分
Pythons sf では微分のためのカスタマイズを行っています。numpy の微分関数:sc.derivative(..) や simpy の微分関数:ts.diff(..) を使えば、関数の微分を行えます。でも これらを直接に使ったのでは複雑になりすぎます。そのため ∂x,∂y,∂z,∂t,∂p,∂p を customize.py に定義しました。これらを使えば関数の微分が簡単に行えます。
∂x,∂y,∂z,∂t,∂p,∂p による微分の前に、そのソースを見ておきましょう。Python は下手な説明文章を見るよりもソースを見たほうが分ることが珍しくありません。
sc.source(∂x)
def __k_P0__(fnAg):
if False:
pass
else:
return sf.P_(0,fnAg)
∂x を使って、こんな具合に計算できます。
f=λ x,y:sin(x+y); ∂x(f) ===============================unpicklable x,y=1,2; f=λ x,y:sin(x+y); ∂x(f)(x,y) =============================== -0.989992494948
もちろん、一変数関数も微分できます。一変数関数ならば、`X 関数と その合成関数を使えるので、下のような Python sf 式が可能です。
∂x( sin(`X^2+1) )(1) =============================== -0.832293685732
∂x(..) は関数を返すのですから、plotGr(..) に引き渡してやれば、グラフを描けます。
plotGr( sin(`X^2+1),-pi,pi );plotGr(∂x( sin(`X^2+1) ), -pi,pi, color=orange)
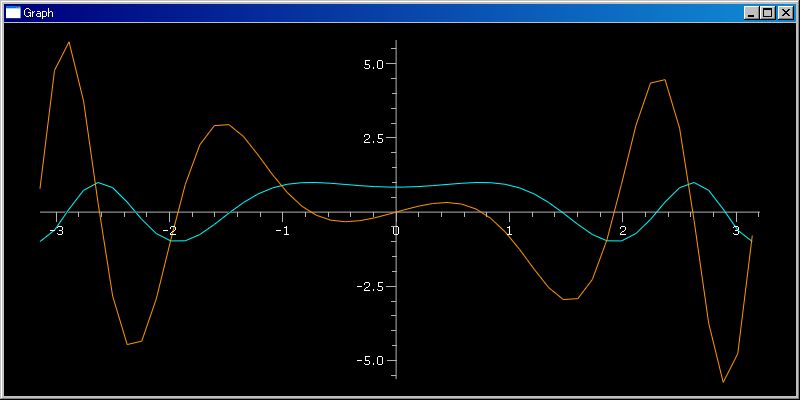
シンボリックな処理をさせるため ts() を実行して sympy を ts 名前空間に取り込ませるとき同時に ∂x(..) 関数も下のように書き換えます。∂x(..) の引数が sympy の symbolic な関数のときは ts.diff(..) を呼び出して symbolic な微分を行わせます。
ts();sc.source(∂x)
In file: D:\lng\Python26\lib\site-packages\pysf\customize.py
def __k_P0__(fnAg):
if ( isinstance(fnAg, ts.Basic)
or isinstance(fnAg, ts.Add)
or isinstance(fnAg, ts.Mul)
or (hasattr(fnAg, 'is_Function') and fnAg.is_Function())
or (hasattr(fnAg, 'is_Pow') and fnAg.is_Pow())
):
return (ts.diff(fnAg, k__bq_x___))
else:
return sf.P_(0,fnAg)
===============================
None
ts() を実行したとき、`x,`y,`z,`t,`p,`q,`n_ を sympy のシンボリックな変数として定義し ts サブ名前空間に取り込んでいます。ts() を呼び出した後は Python sf 式で、これらのシンボリック変数を下のように使えるようになります。
`x^2+`y^2
name 'k__bq_x___' is not defined at excecuting:k__bq_x___**2+k__bq_y___**2
ts();`x^2+`y^2
===============================
x**2 + y**2
ts() 呼び出しにより使えるようになる上のシンボリック変数と ts:sympy モジュール alias 名と customize.py で定義してある ∂x,∂y,∂z,∂t,∂p,∂p を使えば、下のようなシンボリックな Python sf 微分計算式を使えます。
ts();∂x(`x^2+`y^2) =============================== 2*x ts();∂y(`x^2+`y^2+`z^2-`t^2) =============================== 2*y ts();∂t(`x^2+`y^2+`z^2-`t^2) =============================== -2*t ts();∂y( ts.sin(`x^2+`y^2+`z^2-`t^2) ) =============================== 2*y*cos(x**2 + y**2 + z**2 - t**2) ts();∂p( 1/ts.sqrt(`p^2+`q^2) ) =============================== -p/(p**2 + q**2)**(3/2) ts();∂q( 1/(`p^2+`q^2) )^(2/3) =============================== (-2)**0.666666666666667*q**0.666666666666667*((p**2 + q**2)**(-2))**0.666666666666667 # `1r is a sympy rational number defined in customize.py ts();∂q( 1/(`p^2+`q^2) )^(2 `1r/3) =============================== 2**(2/3)*(-q/(p**2 + q**2)**2)**(2/3)
数値微分において ∂x,∂y,∂z は「0 番目の引数の微分」、「1 番目の引数の微分」、「2 番目の引数の微分」の意味です。∂t は「最後の引数の微分」の意味です。シンボリック微分とは異なり、x,y,z,t 文字の識別は行いません。
pos=(1,2); f=λ x,y:x^2+y; ∂x(f)(*pos) =============================== 2.0 # 上の Python sf 式で x,y を入れ替える pos=1,2; f=λ y,x:x^2+y; ∂x(f)(*pos) =============================== 0.999999999998 pos=1,2; f=λ x,y:x^2+y; ∂y(f)(*pos) =============================== 1.0 pos=1,2,3; f=λ x,y,t:x^2+y-3t; ∂t(f)(*pos) =============================== -3.00000000001
数値微分はシンボリック微分とは異なり誤差が付きまといます。微分の微分を行うと、さらに誤差が重なります。微分の微分の微分を行うと三桁程度の精度にまで落ちてきます。ご注意ください。
# rank 2 derivative f=(∂x(∂x(`X^2)));[f(x) for x in range(10)] =============================== [1.9999999999999998, 1.9999999989472883, 2.0000000433562093, 1.9999999878450581, 1.9999998990272161 , 1.9999999878450581, 2.000000165480742, 2.000000165480742, 2.000000165480742, 2.000000165480742] # rank 3 derivative f=∂x(∂x(∂x(`X^3)));[f(x) for x in range(10)] =============================== [6.0, 6.0000338031329647, 6.0002003365866585, 5.9996452250743459, 5.9960925113955454 , 6.0005334034940461, 5.9934279761364451, 5.9969806898152456, 5.9969806898152456, 5.9969806898152456]
Jacobian
customize.py に ∂J:Jacobian 微分を定義してあります。これは数値微分に限って計算します。でも任意個数の引数の関数でも計算できるので、意外と便利です。
下のように、scalar 関数の Jacobian は gradient になります。
pos=1,2; f=λ x,y:1/norm(x,y);∂J(f)(*pos) =============================== [-0.08944272 -0.17888544] ---- ClTensor ---- pos=1,2,3; f=λ x,y,z:1/norm(x,y,z);∂J(f)(*pos) =============================== [-0.01909009 -0.03818018 -0.05727027] ---- ClTensor ---- pos=1,2,3,4; f=λ x0,x1,x2,x3:1/norm(x0,x1,x2,x3);∂J(f)(*pos) =============================== [-0.00608581 -0.01217161 -0.01825742 -0.02434322] ---- ClTensor ---- ∂J([`X,`Y,`Z], inDim=3)(1,2,3) =============================== [[ 1. 0. 0.] [ 0. 1. 0.] [ 0. 0. 1.]] ---- ClTensor ---- ∂J([`X,`Y,`X^2+`Y^2], inDim=2)(1,2) =============================== [[ 1. 0.] [ 0. 1.] [ 2. 4.]] ---- ClTensor ---- r=sqrt(`X^2+`Y^2+`Z^2);∂J([`X/r,`Y/r,`Z/r],inDim=3)(1,2,3) =============================== [[ 0.24817115 -0.03818018 -0.05727027] [-0.03818018 0.19090089 -0.11454053] [-0.05727027 -0.11454053 0.09545044]] ---- ClTensor ---- 0.24817115+0.19090089+0.09545044 =============================== 0.53452248 R3=sqrt(`X^2+`Y^2+`Z^2)^3;`div([`X/R3,`Y/R3,`Z/R3])(1,2,3) =============================== 2.38524477947e-11 r=sqrt(`X^2+`Y^2+`Z^2);`div([`X/r,`Y/r,`Z/r])(1,2,3) =============================== 0.534522483873 r=sqrt(`X^2+`Y^2+`Z^2);`rot([`X/r,`Y/r,`Z/r],inDim=3)(1,2,3) [[ 0.00000000e+00 -1.47104551e-11 -5.88418203e-11] [ 1.47104551e-11 0.00000000e+00 -7.27196081e-11] [ 5.88418203e-11 7.27196081e-11 0.00000000e+00]] ---- ClTensor ----<
下のように、scalar 関数の Jacobian の Jacobian の trace は △:ラプラシアン演算になります。
pos=1,2; f=λ x,y:1/norm(x,y);∂J(∂J(f))(*pos).trace() =============================== 0.0894427185094 pos=1,2; f=λ x,y:log(1/normSq(x,y));∂J(∂J(f))(*pos).trace() =============================== -1.11022302463e-08 pos=1,2,3; f=λ x,y,z:-1/norm(x,y,z);∂J(∂J(f))(*pos).trace() =============================== 1.38777878078e-09 pos=1,2,3,4; f=λ x0,x1,x2,x3:-1/norm(x0,x1,x2,x3);∂J(∂J(f))(*pos).trace() =============================== 0.00608580200123
下のように、scalar 関数の Jacobian の「 Jacobian - Jacobiand.transpose) は rot 演算を意味します。
pos=1,2; f=λ x,y:1/norm(x,y);∂J(∂J(f))(*pos)-∂J(∂J(f))(*pos).t =============================== [[ 0. 0.] [ 0. 0.]] ---- ClTensor ---- pos=1,2,3; f=λ x,y,z:1/norm(x,y,z);∂J(∂J(f))(*pos)-∂J(∂J(f))(*pos).t =============================== [[ 0. 0. 0.] [ 0. 0. 0.] [ 0. 0. 0.]] ---- ClTensor ---- pos=1,2,3,4; f=λ x0,x1,x2,x3:1/norm(x0,x1,x2,x3);∂J(∂J(f))(*pos)-∂J(∂J(f))(*pos).t =============================== [[ 0. 0. 0. 0.] [ 0. 0. 0. 0.] [ 0. 0. 0. 0.] [ 0. 0. 0. 0.]] ---- ClTensor ----
微分形式やテンソル解析になれていないと、最初は このタイプの rot 演算に戸惑うかもしれません。でも、こちらの形式ならば、任意次元の rot を計算できます。三次元以外でも rot 演算が可能です。customize.py には、この意味での `rot(..) 関数を定義してあります。
pos=1,2,3,4; f=λ x0,x1,x2,x3:1/norm(x0,x1,x2,x3);`rot(∂J(f))(*pos) =============================== [[ 0. 0. 0. 0.] [ 0. 0. 0. 0.] [ 0. 0. 0. 0.] [ 0. 0. 0. 0.]] ---- ClTensor ----
シンボリック微分
`x `y `z `t `p `q `n の sympy 変数を customize.py で定義してあり、また ∂x ∂y ∂z ∂t ∂p ∂q 微分関数も customize.py に定義してあるので、シンボリックな微分も Python sf 式で柔軟に記述できます。
ts();∂x(ts.sin(`x)/`x) =============================== cos(x)/x - sin(x)/x**2 ts();∂y(ts.sin(`x `y)/(`x^2+`y^2)) =============================== x*cos(x*y)/(x**2 + y**2) - 2*y*sin(x*y)/(x**2 + y**2)**2 ts();∂y(ts.sin(`x `y)/(`x^2+`y^2)).subs([(`x,1),(`y,2)]) =============================== -4*sin(2)/25 + cos(2)/5 ts();float(∂y(ts.sin(`x `y)/(`x^2+`y^2)).subs([(`x,1),(`y,2)])) =============================== -0.228716955602 ts();(λ x,y:float(∂y(ts.sin(`x `y)/(`x^2+`y^2)).subs([(`x,x),(`y,y)])))(1,2) =============================== -0.228716955602
sympy の関数であっても実数値を返す関数に変換してやれば plot3dGr(..) などを使ってグラフ表示させられます。
ts();plot3dGr(λ x,y:float( (ts.sin(`x `y)/(`x^2+`y^2)).subs([(`x,x),(`y,y)])),[-pi,pi],[-pi,pi])
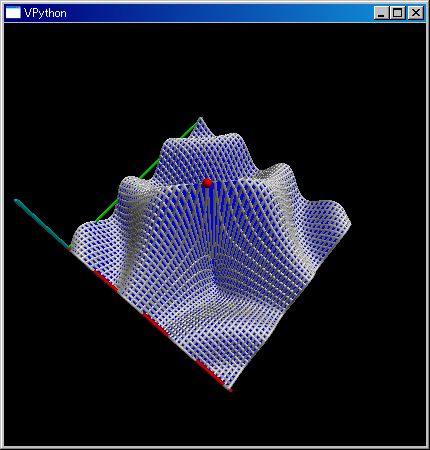
ts();plot3dGr(λ x,y:float(∂y(ts.sin(`x `y)/(`x^2+`y^2)).subs([(`x,x),(`y,y)])),[-pi,pi],[-pi,pi])
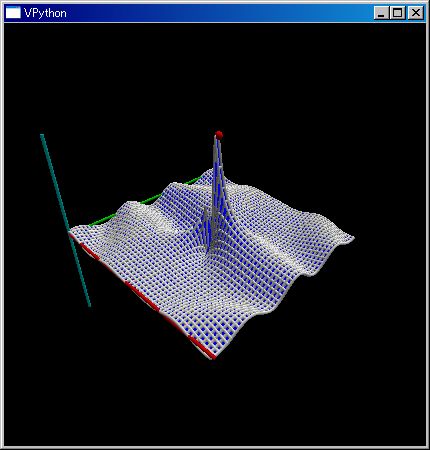
■ 積分
scipy パッケージの scipy.integrate サブ・パッケージモジュールに quad(..) などの定積分関数があるのですが、色々と面倒なので kNumeric.py のなかで下の積分関数を介在させています。
- quadR(realFunction, begin, end):実数値関数の積分
quadR(exp(-`X^2), -sc.inf, sc.inf) =============================== 1.77245385091 # sc.inf == ∞ sqrt(pi) =============================== 1.77245385091
- quadC(complexFunction, realBegin, realEnd):実数引数で複素数値戻り関数の積分
f=0.1Hz`;quadC(exp(-`X^2) exp(2 pi `i f `X), -sc.inf, sc.inf) =============================== (1.60587519197+0j) f=0.1Hz`;quadC(exp(-`X^2) exp(2 pi `i f `X), 0, sc.inf)
- quadAn(fAn, sqPath):複素数引数 複素数戻り値関数の sequence of path に沿った積分値
quadAn(1/`X, [1,`i,-1,-`i,1]) =============================== (6.2831853071795862j, 6.9757369969054392e-14, 6.9757369969054392e-14) #>== (積分値、実数値側の誤差、虚数値側の誤差)の順序 quadAn(1/`X, [2+2`i, -2+2`i, -2-2`i, 2-2`i,2+2`i]) =============================== (6.2831853071795871j, 3.0615980059724259e-14, 6.9757369942584612e-14) quadAn(1/sin(`X), [2,2`i,-2,-2`i,2]) =============================== ((5.5511151231257827e-17+6.2831853071795862j), 7.0920083175434644e-14, 7.0920083175434644e-14) ts();(1/ts.sin(`x)).series(`x) =============================== x/6 + 1/x + 7*x**3/360 + O(x**4)
- quadN(fN, sqXN):N 次元ベクトル引数の N 次元ベクトル戻り値の関数の sqXN:N次元経路シーケンス に沿った積分
vctE = λ vctP:vctP/normSq(vctP);quadN(vctE, ([1,1,0],[1,-1,0],[-1,-1,0],[-1,1,0],[1,1,0]) ) =============================== (2.5967314670465034e-18, 3.0615980059724259e-14) vctE = λ vctP:vctP/normSq(vctP);quadN(vctE, ([1,1,0],[2,2,0]) ) =============================== (0.6931471805599454, 7.6954795931166216e-15) #>== (積分値、誤差) vctE = λ vctP:vctP/normSq(vctP);quadN(vctE, ([1,0],[1,1],[0,1],[1,0])) vctE = λ vctP:vctP/norm(vctP);quadN(vctE, ([1,0],[1,1],[0,1],[1,0])) =============================== (0.0, 2.7802086910857742e-09) vctE = λ vctP:vctP log(norm(vctP));quadN(vctE, ([1,0],[1,1],[0,1],[1,0])) =============================== (0.0, 7.0976215179519565e-10)
scipy.odeint(...) 常微分方程式の数値解
scipy.integrate には常微分方程式を解く関数 odeint(..) が備わっています。
sy();help(si.odeint)
odeint(func, y0, t, args=(), Dfun=None, col_deriv=0, full_output=0, ml=None, mu=None, rtol=None, atol=None, tcrit=None, h0=0.0, hmax=0.0, hmin=0.0, ixpr=0, mxstep=0, mxhnil=0, mxordn=12, mxords=5, printmessg=0)
Integrate a system of ordinary differential equations.
Solve a system of ordinary differential equations using lsoda from the
FORTRAN library odepack.
Solves the initial value problem for stiff or non-stiff systems
of first order ode-s::
dy/dt = func(y,t0,...)
where y can be a vector.
Parameters
----------
func : callable(y, t0, ...)
Computes the derivative of y at t0.
y0 : array
Initial condition on y (can be a vector).
t : array
A sequence of time points for which to solve for y. The initial
value point should be the first element of this sequence.
args : tuple
Extra arguments to pass to function.
Dfun : callable(y, t0, ...)
Gradient (Jacobian) of func.
col_deriv : boolean
True if Dfun defines derivatives down columns (faster),
otherwise Dfun should define derivatives across rows.
full_output : boolean
True if to return a dictionary of optional outputs as the second output
printmessg : boolean
Whether to print the convergence message
Returns
-------
y : array, shape (len(y0), len(t))
Array containing the value of y for each desired time in t,
with the initial value y0 in the first row.
・
・
d^2(vctX)/dt^2 = - vctX/normSq(vctX) 初期条件 位置 [1,1] 速度 [1,0.5]
odeint が扱えるのは一階の常微分方程式なので、速度も含めた四つの要素からなるベクトルの常微分方程式に変換します。
d X[0]/dt = X[2] d X[1]/dt = X[3] d X[2]/dt = -X[0]/normSq(X[:2]) d X[3]/dt = -X[1]/normSq(X[:2]) 初期条件 位置 [1,1] 速度 [1,0.5]
sy();f=λ x,t:sc.r_[x[2:], -x[:2]/normSq(x[:2])];si.odeint( f, [1,1,1,0.5], klsp(0,5)) #>== r_[vct1, vct2] は vct1 と vct2 を繋げたベクタを作ります sy();f=λ x,t:[x[2],x[3], -x[0]/(x[0]^2+x[1]^2), -x[1]/(x[0]^2+x[1]^2)];si.odeint( f, [1,1,1,0.5], klsp(0,5)) =============================== [[ 1. 1. 1. 0.5 ] [ 1.09948036 1.04850109 0.9502175 0.4513988 ] [ 1.19399814 1.09226499 0.90267724 0.40700463] [ 1.28376596 1.13168028 0.85707181 0.36605682] [ 1.36896773 1.16706795 0.81314302 0.32797938] [ 1.4497631 1.19869719 0.77067287 0.292326 ] [ 1.52629118 1.22679669 0.72947583 0.25874392] [ 1.59867358 1.25156282 0.68939263 0.22694952] [ 1.66701673 1.27316581 0.6502853 0.1967113 ] [ 1.73141394 1.29175437 0.61203327 0.16783778] [ 1.79194694 1.30745936 0.57453019 0.14016871] [ 1.84868724 1.32039656 0.53768139 0.11356852] [ 1.90169719 1.33066901 0.50140187 0.08792142] [ 1.95103089 1.33836872 0.46561458 0.06312765] [ 1.99673492 1.34357826 0.43024911 0.03910051] [ 2.03884896 1.3463719 0.39524045 0.01576411] [ 2.07740631 1.34681664 0.36052809 -0.00694846] [ 2.11243426 1.34497304 0.32605516 -0.02909658] [ 2.14395449 1.34089595 0.2917677 -0.0507333 ] [ 2.17198324 1.33463508 0.25761402 -0.07190632] [ 2.19653162 1.3262355 0.22354414 -0.09265873] [ 2.21760569 1.3157381 0.18950928 -0.11302976] [ 2.23520654 1.30317995 0.15546131 -0.13305525] [ 2.24933041 1.2885946 0.12135234 -0.15276815] [ 2.25996861 1.27201237 0.08713423 -0.17219894] [ 2.26710753 1.25346059 0.0527581 -0.19137594] [ 2.2707285 1.23296379 0.01817389 -0.21032558] [ 2.27080765 1.21054389 -0.01667018 -0.22907269] [ 2.26731575 1.18622035 -0.05182814 -0.24764068] [ 2.26021787 1.16001031 -0.08735689 -0.26605175] [ 2.24947314 1.1319287 -0.12331689 -0.284327 ] [ 2.23503429 1.10198833 -0.15977288 -0.30248658] [ 2.21684719 1.07020002 -0.19679487 -0.32054978] [ 2.19485024 1.03657265 -0.23445908 -0.33853512] [ 2.16897371 1.00111326 -0.27284931 -0.35646032] [ 2.13913887 0.96382712 -0.31205836 -0.37434237] [ 2.10525696 0.92471778 -0.35218992 -0.39219739] [ 2.06722803 0.88378724 -0.39336082 -0.41004052] [ 2.02493939 0.84103597 -0.43570387 -0.42788569] [ 1.97826385 0.79646314 -0.4793714 -0.44574519] [ 1.92705746 0.75006674 -0.5245399 -0.46362906] [ 1.87115685 0.7018439 -0.57141585 -0.48154415] [ 1.81037564 0.65179128 -0.62024371 -0.49949265] [ 1.74450021 0.59990564 -0.67131624 -0.51746985] [ 1.67328398 0.54618471 -0.72498884 -0.53546062] [ 1.59644009 0.49062853 -0.78169956 -0.55343382] [ 1.51363161 0.4332415 -0.84199738 -0.57133321] [ 1.42445825 0.37403565 -0.90658383 -0.58906213] [ 1.32843779 0.31303598 -0.97637568 -0.60645702] [ 1.22497954 0.25028953 -1.05260281 -0.62323912]]
sy();f=λ x,t:[x[2],x[3], -x[0]/(x[0]^2+x[1]^2), -x[1]/(x[0]^2+x[1]^2)];plotTrajectory(si.odeint( f, [1,1,1,0.5], klsp(0,5))[:,:2])
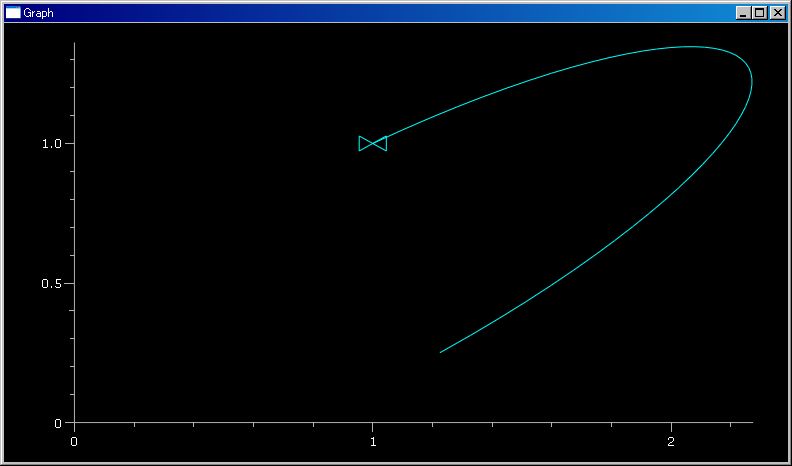
odeint 常微分方程式の数値解
常微分方程式系の既知関数が時間に依存しないときに限定してワンライナーでも使える odeint(..) 関数を用意しました。時間引数が入らないため、既知関数を多変数関数として記述できます。Laplace 変換では s^2-2s+26 と表される発散系を解いてみます。
;;plotGr(odeint(λ x,y:[y, 2y-26x],[0.01,0])(10, 256)[:,0])

クリップされた発振のような非線形方程式でも簡単に解けます。
;;plotGr(odeint(λ x,y:[0 if x>1 and y>0 else 0 if x<-1 and y<0 else y, 2y-26x],[0.01,0])(10, 256)[:,0])

■ Python sfファイル実行
複雑な計算をさせるときには、ワンライナーで書くべきではありません。可読性を犠牲にしてまでワンライナーを使うべきではありません。このときは "-fs" オプションをつけて Python sf プリプロセッサに文字列変換のみを行わせます。Python sf でに -fs オプションの後にファイル名を指定すると、プリプロセスだけをした結果を __tempConverted.py ファイルに書き出します。次のような具合です。ちなみに「-fs」 は convert File and Skip execution から決めました
//@@
def f(x,y):
return ~[sin(x)+y^2, y cos(x)]
def g(x,y):
return ~[sin(x) y, cos(x)]
#return ~[[sin(x) y, cos(x)],[tan(x) y, sinh(x+y) x]]
px=(1,2)
pp(∂J(λ x,y: f(x,y) g(x,y))(*px))
print
pp(∂J(f)(*px) g(*px) + f(*px) ∂J(g)(*px))
//@@@
//copy \#####.### temp.py /y
//sfPP.py -fs temp.py
//__tempConverted.py
[ 4.32242, 11.0977]
[ 7.39293, 1.53359]
私はエディターで「//@@ .... //@@@ の間にあるテキストを C:\#####.### ファイルに書き込み、その次にある // で始まるコマンドを実行していくマクロ」を作っています。このマクロも便利です。コンソール・モードを持っているエディタをお使いならば、このマクロを作っておくと、Python sf に限らず、任意の言語一般に使えて便利ですよ。
短いテスト・プログラム・コードを一つのファイルに時系列に従って記録していけます。このマクロを Python に限らず、C++/STL/boost、Ruby、perl, OCaml, erlang, Java などにも使っています。短いテストコードを何百も溜め込んでいます。コンパイル・オプション、実行オプションまで含めて、必要な情報は全て残していけます。何時でも再実行できます。本当に便利ですよ。
このような WZ エディタのマクロも、ここに公開してあるので、WZ エディタ使いの方はご利用ください。その他のエディタの方は、是非とも、ことようにエディタのマクロを作ってみてください。
このようなエディタのマクロのおかげで、この html ファイルに書いてある Python sf 式は、全て書くと同時に再チェックしていっています。たんに 「ctrl + O -< E」 のキー操作だけで、勝手に temp.py ファイルを作り、「sfPP.py -fs temp.py」 を実行させ、プリプロセッサに __tempConverted.py ファイルを作らせ、__tempConverted.py を実行させられるからです。
ちなみに、上の Python sf ファイル実行は、ベクトル値を返す関数の内積に Jacobian 微分を働かせたときにも (f g)' == f' g + f g' の分配則が成り立たないことを確認する数値実験です。∂J に汎用の Jacobian 微分関数を割り振るように、後で述べる customize.py ファイルに登録してあります。
Python sf プリプロセッサが生成するファイル
ファイル実行のために Python sf プリプロセッサが吐き出した __tempConverted.py ファイルを見てやると、その働きが良く判ります。
type __tempConverted.py
from __future__ import division
# -*- encoding: cp932 -*-
from sf import *
from sf.customize import *
if os.path.exists('.\sfCrrntIni.py'):
from sfCrrntIni import *
def f(x,y):
return krry([[sin(x)+y**2, y * cos(x)],[tan(x), sinh(x+y)]])
def g(x,y):
return krry([[sin(x) * y, cos(x)],[tan(x), sinh(x+y)]])
px=(1,2)
pp(k__Round_J___(lambda x,y: f(x,y) * g(x,y))(*px))
pp(k__Round_J___(f)(*px) * g(*px) + f(*px) * k__Round_J___(g)(*px))
「from __future__ import division」は整数/整数の割り算のとき float 値を返すようにさせています。これがないと 2/3 は 0 になってしまいます。
Python 3000 では、デフォルトで整数/整数は float 値にする仕様に変わります。でも 2.x バージョンの python は「from __future__ import division」がないと整数/整数は整数になってしまいます。
//@@ a=2/3 print a //@@@ //copy \#####.### temp.py /y //python temp.py 0
実数の数値計算が主なとき、これでは困ります。2.0/3 と書けばよいのですが、どうしても2/3 と書いてしまいます。通常書いている数式が 2/3 と書くからです。しかも、上のような二行だけでしたら、直ぐに気づきます。でも 20 行のコードの中に、このミスが紛れ込むと簡単には分かりません。何かおかしいからとデバッガで何十分もかけておって初めて割り算の書き間違いだと気づくことが何度も発生します。これを避けるために Python sf では、無条件で「from __future__ import division」を有効にしています。ワンライナーのときも同じです。
「from sf import *」により、 Python sf の基本機能:行列演算、表示関数などの名前空間を global 変数に取り込んでいます。kzrs(3) と書くだけで sf.py に定義してある、0 ベクトル/行列を生成する kzrs 関数をで呼び出せます。「import sf;sf.kzrs(3)」 などと冗長な書き方をせずに済ませられるようにしています。
「from customize import *」も同様に customize.py ファイル内で宣言・定義してある変数名、関数名、モジュール名を global 変数に取り込ませています。customize.py はユーザーが必要とするデフォルトの名前空間を指定するために設けています。ユーザー側で customize.py を編集し、必要なユーザー環境に向けてカスタマイズしてください。
■■ scipy
scipy si モジュール
積分の quadR は si.quad を、より単純に使えるように kNumeric で少しだけ修正したものです。
scipy sl モジュール
numpy.linalg よりも scipy.linalg の方が、多くの機能を持っています。行列の sin/cos 関数は numpy.linalg にはありませんが、scipy.linalg には実装されています。
sl に scipy パッケージの linalg モジュールを割り当てて Python sf 名前空間に入れてあります。これにより、linalg モジュールにある線形代数関連の関数を使えるようりなります。例えば行列の sin 関数の計算を次のように行えます。
sy();H = `σx + `σy+`σz; sl.sinm(H) =============================== [[ 0.5698601+0.j 0.5698601-0.5698601j] [ 0.5698601+0.5698601j -0.5698601-0.j ]]
上の sinm の計算は要素ごとの sin を計算させているのではありません。下の計算値が上の値と同じであることからも分るように、行列自体の sin を計算させています。
sy();N,H =20, `σx + `σy+`σz; sum([(`i H)^(2n+1)/sy.factorial(2n+1) for n in range(N)])/`i =============================== [[ 0.5698601+0.j 0.5698601-0.5698601j] [ 0.5698601+0.5698601j -0.5698601+0.j ]] ---- ClTensor ---- H=`σx + `σy+`σz; (expm(`i H) - expm(-`i H))/(2`i) =============================== [[ 0.5698601+0.j 0.5698601-0.5698601j] [ 0.5698601+0.5698601j -0.5698601+0.j ]] ---- ClTensor ----
sy();H = `σx + `σy+`σz; sl.cosm(H) =============================== [[ -1.60556539e-01 +0.00000000e+00j 1.11022302e-16 -1.11022302e-16j] [ 1.66533454e-16 +1.66533454e-16j -1.60556539e-01 +0.00000000e+00j]]
■■ sympy
sympy のバージョンは 2010 年 5 月の段階で 0.6... のバージョンであり、完成したものではありません。でも基本的なところは動いています。十分に実用できる団塊に到達しています。 微分 積分 行列 ts();ts.symbols('xy');x+yS("...")
S(文字列) により、文字列を sympy の式として評価します。結構便利です。
ts();x,y,z=ts.symbols('xyz');x+y+ ts.S('x+y+z')
===============================
z + 2*x + 2*y
ts();x,y,z=ts.symbols('xyz');ts.sin(x)+y+ ts.S('sin(x)+y+z')
===============================
z + 2*y + 2*sin(x)
sympy 有理数
ts();ts.sin(`1f/5) =============================== sin(0.2) ts();ts.sin(`1r/5) =============================== sin(1/5)mailto: your@email.ne.jp
Last update: