PythonSf は Python Scientific Functional math software の略です。電卓の手軽さで matlab/mathematica クラスの計算処理を可能にします。PythonSf は数学ソフトの L.L:Scripting Language です
あえてコンソール・プログラムとすることで、日常メモ書き数式を使ったエディタ上での計算を可能にし、数式入力のためのユーザー・インターフェースをユーザーごとに最適なものにします。プリプロセッサを介在させることで、積演算子の省略を可能にするなど数学での数式記述に近いメモ書き数式記述と Python との upper compatibility を両立させます。また名前空間の拡張とカスタマイズ機能により、ユーザーの専門分野に合わせた数式記述を可能にします。これにより可読性を保ちながら、短い計算式:ワン・ライナー記述を可能にします。たぶん大多数のユーザーが、日常計算の九割以上をワンライナーで済ませられるでしょう。また任意の Python ワン・ライナー・コードの実行も可能です。次のような具合です。
PythonSf ワンライナー
# 数値の加減乗除べき乗算
(1-2*3/4)^5
===============================
-0.03125
# sin(1/x) value at x=pi
sin(1/`X)(pi)
===============================
0.312961796208
# 数値微分値: sin(1/x) value at x=pi
∂x( sin(2/`X) )(`π)
===============================
-0.162946719226
# シンボリック微分: sin(1/x)
ts(); ∂x( ts.sin(1/`x) )
===============================
-cos(1/x)/x**2
# Groebner 基底をシンボリックに計算する
ts();x,y,z=ts.symbols('x y z');f1,f2,f3=[x+y^2+3z^2-4, 4y^2-5,y^4-5z-10]; ts.groebner([f1,f2,f3], [x,y,z])
===============================
[-5/4 + y**2, 1483/256 + x, 27/16 + z]
# 行列とベクトルの積演算
# |1,2| * |5|
# |3,4| |6]
mt,vc=~[[1,2],[3,4]], ~[5,6]; mt vc
===============================
[ 17. 39.]
---- ClTensor ----
# W:ワット、A:アンペア単位付きの数値計算
ts(); wattage,current=100W`,2.3A`; wattage/current^2
===============================
18.9035916824197*V`/A`
# Bool 体係数多項式の商と剰余
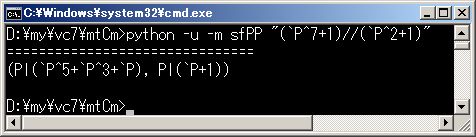
(`P^7+1)/(`P^2+1)
===============================
(Pl(`P^5+`P^3+`P), Pl(`P+1))
x=`P; (x^7+1)%(x^2+1)
===============================
`P+1
# 楕円関数:第一種の不完全/Jacobi 楕円関数の計算
φ,m=pi/3,0.6; sy(); u=ss.ellipkinc(φ,m); ss.ellipj(u,m)
===============================
(0.8660254037844386, 0.50000000000000011, 0.74161984870956643, 1.0471975511965976)
# Sn(4) 置換群における 置換集合:{Sb(2,3,0,1), Sb(1,0,3,2),Sb(1,3,2,0)} の左剰余類
=:SS4; SS4/{Sb(2,3,0,1), Sb(1,0,3,2),Sb(1,3,2,0)}
===============================
kfs([Sb(0,1,2,3), Sb(0,1,3,2), Sb(0,2,1,3), Sb(0,2,3,1), Sb(0,3,1,2), Sb(0,3,2,1)])
# 数値 1234 と文字列 '1' の hash コードを確認する Python テスト・コード
hash(1234), hash('1')
===============================
(1234, 1977051568)
# グラフ描画: sin(1/x) を [0.2, pi] 領域で
plotGr( sin(1/`X), 0.2, pi )
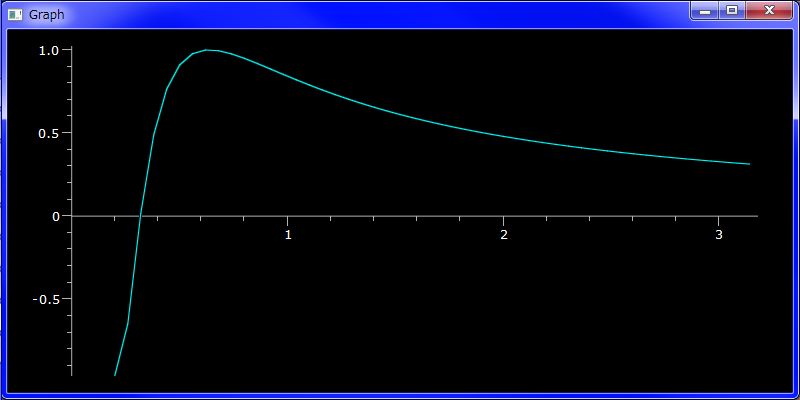
上の数式で、`X は back quote ` 記号により拡張された名前空間に属する変数名です。カスタマイズ機能を使って、`X に加減乗除べき乗算が可能な恒等関数を割り振っています。これにより日常でのメモ書きに近い、計算可能な任意の有理関数を記述できます。同様に `P には、ブール体係数の単項一次多項式(x 相当) を割り振ってあります。これも加減乗除べき乗算可能であり、殆どメモ書き数式と同じままにブール体系数多項式を計算できます。
特殊記号の漢字∂∇□△ およびギリシャ文字漢字を使えるようにすることでメモ書き数式を数学教科書での記述に近いものにできています。∂x(...) による微分表記の可読性の高さを、漢字文化圏の方には理解してもらえるはずです。
~[...] 表記により行列やベクトルを表記します。グラフ描画は plotGr(..) に関数と表示領域パラメータを与えるだけです。どちらも最小の手間で行列計算処理すること、グラフを描くことを狙っています。
PythonSf では、多くの計算をワンライナーで行います。複数の Python 式/文を使うときはセミコロンを間に挿入します。上の全ての例がワンライナーで書かれています。
上の計算例で print 命令がないにもかかわらず、最後の式の値が出力されていることにも注目ください。 ワンライナーで複数の式/文を実行するとき、ユーザーが知りたい計算値は、大部分の場合最後の式の値なので、それを自動的にコンソールに出力させています。
数学での数式記述は、短さと可読性の両立させています。PythonSf 数式でも短く可読性の高い記述を追求しています。ワンライナーの最終式の値の自動出力は その一例です。
上で「 matlab/mathematica クラスの計算処理を可能にする」と書きましたが、これは誇大妄想でも、大言壮語でもありません。PythonSf は Python upper compatible であり、Python package/module として配布されている全ての機能を利用できるからです。
PythonSf は、sy() 関数呼び出しにより SciPy および、その sub package を import します。SciPy package は、実用的には十分なほどに matlab の多くの数値計算機能を Python で実装しています。sy() により special function sub package を ss のラベルに import してあるので、上の計算例のように、ss の下で楕円関数 ellipkinc, ellipj を呼び出しています。
また ts() により SymPy を import し、同時に `x,`y,`z,`t ラベルに SymPy のシンボリック変数を割り当てます。これによりシンボリックな演算操作が可能です。上の計算例ではシンボリック微分を行っています。
さらに Numpy の 行列・ベクトルを拡張し一般体も扱えるようにしてあり、Zp(N) や、それを係数とする多項式も扱えるようにしてあります。置換群 Sn(N) も扱えます。Laplace 変換/z 変換のための有理式クラスも用意してあります。 標準の PythonSf だけで学部数学程度の計算能力を備えています。
もっと高度な数学機能が必要なときは、御自分で Python 言語を使い、また PythonSf のカスタマイズ機能を使って実装ください。簡単です。
これらの膨大な数学領域を扱えるにも関わらず、Python を知っているならば、PythonSf の学習コストは一日程度です。文法は Python であり、プリプロセッサで行っているのは、数学での数式記述に近づけることだけであり、Python Upper Compatible を保っているからです。ss が special function subpackage であること、`x,`y,`z が SymPy のシンボリック変数であることなどの、ラベルと対応する Python object を覚えるだけで、Python 文法と数学知識から多くの PythonSf 式が 予測・類推できます。上の PythonSf 式例を見ただけで、多くの方は関数電卓以上の計算ができるようになっていると思います。
あなたが Python ユーザーであるならば、matlab/mathematica など既存数学ソフトのヘビー・ユーザーであっても、PythonSf を強く勧めます。PythonSf は数学ソフトの L.L:Light weight/Script Language です。ブール体係数多項式の商と剰余を計算させたときのように、メモ書き数式と殆ど同じような短い式で記述・計算させられます。 他数学ソフトのヘビー・ユーザーであっても、PythonSf の方が数式記述が短く簡単に計算させられるので、こちらでの計算のほうが多くなるはずです。
PythonSf の方が数式記述力の多くが次に述べるカスタマイズ機能によってもたらされます。
ユーザーの専門分野によって望ましい数学ソフト機能は異なります。多くのユーザーが、自分に合わせて数学ソフトをカスタマイズする必要に迫られるはずです。逆に自由にカスタマイズできる数学ソフトを望むユーザーも多いはすです。
PythonSf はカスタマイズ・モジュール customize.py/sfCrrntIni.py の中で拡張された名前空間の短いラベルに、Python program を使って、望ましい機能の Python object を割り当てることによりカスタマイズを実装します。ここで customize.py は python path に置かれます。sfCrrntIni.py は current directory に置かれます。PythonSf は、数式を実行する前に from customize import *, from sfCrrntIni import * を行います。すなわち customize.py/sfCrrntIni.py で宣言された変数、関数、クラスとクラス・インスタンスの名前は全てグローバル変数名前空間に入り込んできます。
例えば上の例で `P がブール体係数の単項一次多項式でした。これは customize.py の中で下のような Python program を書くことで実現されています。そしてプリプロセッサが `P を k__bq_P___ に置き換えることで、先のブール体系数多項式の割り算式 (`P^7+1)/(`P^2+1) は Python は、Python program code として実行できる文字列になります。
class PB(oc.Pl):
"""' BF:Bool Field `P polynomial '"""
def __init__(self, *sqAg):
oc.Pl.__init__(self, dtype = oc.BF, variable='`P', *sqAg)
k__bq_P___ = PB(1,0)
customize.py/sfCrrntIni.py の中で何をどのように import するのか、どんな変数名に何を割り当てるのかはユーザーの自由です。k__bq_P___ に別の機能を持ったインスタンスを割り当てれば、`P は別の意味を持つことになりますす。
ここで、back quote:` による名前空間の拡張に注目下さい。もし一文字 P にブール体係数の単項一次多項式を割り振り振るのは無謀すぎます。一文字 P は短すぎます。どこかで名前の衝突が発生し予定外の動作になる危険性が潜んできます。でも `P ならば、名前の衝突は PythonSf 式の範囲だけに限られます。名前の衝突に神経質になる必要はありません。すなわち短い PythonSf 式で複雑な計算をさせられるようになります。 (`P^7+1)/(`P^2+1) だけでブール体系数多項式の割り算を計算できてしまいます。
Current directory に置かれる sfCrrntIni は、そのディレクトリに限ったカスタマイズ・プログラム・コードを記述します。特定の分野に限って、そこで必要となる前提数式を sfCrrntIni.py のグローバル変数に書き上げておけば、短い PythonSf 式で数多くの処理ができてしまいます。
適切にカスタマイズしてやることで日常計算の九割以上が PythonSf 式の a one-liner で計算できてしまうようになります。(`P^7+1)/(`P^2+1) で計算させるような真似を、ユーザー側で自由に設定できます。
貴方が考えている数式群の前提を、明示的にカスタマイズ・ファイルに凝縮していくことにも注目ください。 sfCrrntIn.py などのカスタマイズ・ファイルには何度も参照される重要な関数・式のみが凝縮して残されていきます。一年後でも、そのカスタマイズ・ファイルを読み直せば、当時考えていた文脈が直ぐに戻ってきます。そしてメモに残されているワンライナー PythonSf 式は、そのカスタマイズ・ファイルの下で、何時でも用意に再実行可能です。
容易に再実行可能なのは、その前提が凝縮してた蓄積された sfCrrntIni.py だけに PythonSf one-liners の計算が依存しているからです。それとは別に昔大量に行われる計算には依存しないからです。One-liner の一行だけで計算が完結しているため、それ以前の計算とは独立しているからです。
Mathematica などの notebook では、多くの場合計算式の独立性が成り立ちません。それらのnotebook でも、計算過程を保存でき後で参照できます。でも、notebook に残っている大部分の式がゴミです。そしてゴミと後で再利用する大事な式や値との区別が不明確です。書いた直後ならば重要な式・考えている文脈が頭の中に残っているので、そのような notebook でも役にたちます。でも一年後などでは notebook を最初から読み下して昔考えていた文脈を再構築せねばなりません。ゴミ溜めの中から重要な式を拾い出して、昔考えていた文脈を頭の中に再構築するには大変な労力が必要となります。
PythonSf は CUI:コンソール・ソフトです。GUI ではありません。マウスを使うのは 3D グラフを様々の角度から見るときぐらいです。 計算ソフトはグラフ表示を除いたら GUI に向きません。人間が数式文字列を与えて、コンピュータがそれを計算して結果の文字列を返すだけだからです。計算途中で人間とコンピュータが対話する必要性がないからです。∂ などの漢字記号を許せば、CUI の範囲のメモ書き数式でも、数学教科書での数式表記に近づけられることも CUI の使用を助けます。
コンピュータに与える数式文字列の入力は使い慣れたエディタで行うのが適切です。文字列の取り扱いで使い慣れたエディタに勝るものはないからです。エディタで計算させたい数式文字列を入力し終わったら、エディタのコンソール処理マクロを使って PythonSf プリプロセッサの CUI インターフェース経由で計算処理をさせ、計算結果を待つだけです。
PythonSf での計算処理はエディタを使わずに、コンソールで直接行わせることも可能です。先のブール体係数多項式の計算は次のようにコンソールでも行わせられます。

要は sfPP.py プリプロセッサ・モジュールに PythonSf 式文字列を与えることで計算処理を行うわけです。ただ「一日に何十回、何百回も python -u -m sfPP "..." と決まりきった文字列を入力すること」と「計算結果をコピーすること」をエディタ側で行うことで手間を省くことを推奨しているわけです。この"python -u -m sfPP"文字列とカーソル下の PythonSf 式文字列とを繋ぎ合わせてコンソール側に実行させるエディタ・マクロを作って使うことを強く推奨します。Vim エディタでの PythonSf 式を実行するマクロの配布と使い方はこちらで詳述します。PythonSf を評価するだけならば、人間がコンソールから手入力することもありだと思います。
PythonSf をエディタ上で計算させることと、分野に合わせたカスタマイズによる短い数式文字列で計算できることから、PythonSf では one-liners による計算が多用されます。
ユーザーに合わせたカスタマイズを施すことで、日常計算の九割以上を PythonSf の自然なワンライナーで計算できてしまいます。これにより数学を使った思考が変わります。群論、圏論、特殊・一般相対論など難しい教科書を抽象的なまま式を写経して勉強しなければならなかった分野で、 PythonSf を使って具体的に計算確認しながら読み進めていけるようになります。これにより短時間に各分野を習得できるようになります。
ここで「自然な」とは「if then else 構文を含まない」ことを意味しています。計算処理では、普通のプログラムより自然なワンライナーで記述できる場合が多くなります。数学の世界では、理論が十二分以上に整理し尽くされていることが多いので、if then else の場合分けを必要としないことが多いからです。if then else がなければ、そのプログラムは 1 行目から始まるコードをインデントなしで並べていくだけです。インデントなしで単純に縦に並んだコードならば、それを横に並べてワンライナーにしても可読性の悪化は限られます。
自然なワンライナーに for ループやリスト内包表記は含めます。リスト内包表記の後ろに付けられる if 式も含めます。これらは可読性の妨げになりません。ワンライナーの for ループで実行できる文は一つだけであり、インデントを必要としないからです。また multiple iterator:mitr(..) ジェネレータを使うことで、多重ループもワンライナーで自然に扱えます。
ワンライナーにすることで、一つの纏まった機能を容易に再利用可能になります。エディタの一行コピー・ペーストと必要に応じた一部の修正による計算操作の容易性の意味だけではなく、思考での容易さにも注目してください。ワンライナーは、その一行で一つの纏まった機能として完結しています。前後の文脈に影響されません。その一行は、一年後でも、そのワンライナーだけで完結して、一つのシステムとして纏まって動くのです。このようなワンライナーは思考を積み重ねていく上での一つの部品ユニットとしても再利用できるのです。
もちろん、無理なワンライナーは避けるべきです。作者自身が 処理内容を読み取れないないようなワンライナーは本末転倒です。PythonSf でも、もちろんブロック記述も可能です。ワンライナーが無理筋なときは積極的にブロック記述にしてください。それでも通常の Python コードの数分の 1 のコード記述量で済むのですから。
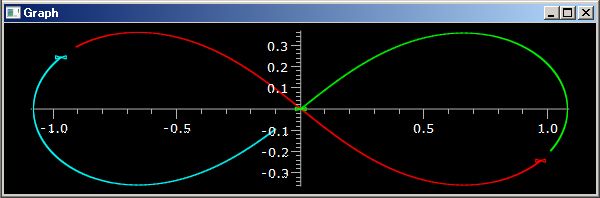
百聞は一見にしかずです。三つの粒子がニュートン力学に従って 8 の字軌跡を描く様子を計算する下の PythonSf スクリプトを見てください
PythonSf ブロック
//@@
# initial positions/vectors
inV=[-0.97,0.243, # 0th particle initial position
0.97,-0.243, # 1st parcitle initial position
0,0, # 2nd parcitle initial position
-0.466,-0.432, # 0th particle initial velocity
-0.466,-0.432, # 1st particle initial velocity
0.932,0.864] # 2nd particle initial velocity
# N particle problem
N=len(inV)//4
# get force to j-th particle from k-th particle
getFV=λ v,i,k:(λ r=krry(v[2k:2k+2])-krry(v[2i:2i+2]):r/norm(r)^3 if norm(r)!=0 else ~[0,0])()
# sum up forces to j-th paticle
sumFc=λ v,j:sum([getFV(v,j,k) for k in range(N) if j!=k])
# define function:fnc which drives a differential equation dv/dt == fnc(*v).
# kOde(...) needs a fnc(x0,x1,...) whick parameter is expanded.
fnc= λ *v: np.r_[v[2N:],(~[sumFc(v,j) for j in range(N)]).r]
# solve the differential equation numerically untill 2 second on 400 points
# kOde(...) returns 400 x 2N data
mt=kOde(fnc,inV, 2 s`,400)
# draw the trajectories of 3 particles using mt data
pt=plotTrajectory
pt(mt[:,:2])
pt(mt[:,2:4],color=red)
pt(mt[:,4:6],color=green)
//@@@
" fnc= λ *v: np.r_[v[2N:],(~[sumFc(v,j) for j in range(N)]).r]" の部分が少しばかり技巧に走っていますが、その他は Python と Numpy に少し詳しければ何の処理をしているのか推測できると思います。この技巧は kOde(...) 上微分方程式のソルバーがベクトル値しか受け付けないため、三個の粒子の位置と速度のベクトル微分方程式を、一個のベクトルだけによる微分方程式で扱うための対策が入っているためです。それを短いワンライナーで記述するために技巧に走っています。その技巧にしても、次の節の説明を読んでもらえば、また Numpy 行列のメソッドに詳しければ容易に読み下せる内容です。
このスクリプトを実行させると、上図のような 8の字軌跡を描きます。
上のスクリプトでは他人様に読んでもらうためにコメントを追加し、改行や空行を挿入していますが、それらは実際の処理には必要ありません。このスクリプトから それらを取り去れば、Python 文が if then else 無しで、すなわちインデント無しで縦に並んでいるだけになります。ならば、これを横に並べてワン・ライナーにできます。実際に下のワン・ライナーでも全く同様に動きます。また この程度のコード量は 27 インチ LCD の全画面ならばワン・ライナーで表示できます。
PythonSf ワンライナー
inV=[-0.97,0.243, 0.97,-0.243, 0,0, -0.466,-0.432, -0.466,-0.432, 0.932,0.864]; N=len(inV)//4; getFV=λ v,i,k:(λ r=krry(v[2k:2k+2])-krry(v[2i:2i+2]):r/norm(r)^3 if norm(r)!=0 else ~[0,0])(); sumFc=λ v,j:sum([getFV(v,j,k) for k in range(N) if j!=k]); fnc= λ *v: np.r_[v[2N:],(~[sumFc(v,j) for j in range(N)]).r]; mt=kOde(fnc,inV, 2 s`,400); pt=plotTrajectory; pt(mt[:,:2]); pt(mt[:,2:4],color=red); pt(mt[:,4:6],color=green)
上の意味の分かりにくい初期数値パラメータの羅列に物理単位系を追加してやれば、この PythonSf 式のワンライナーの塊りが、三体問題の求解の意味を持っていることを表現できます。このスクリプトの作者は、ニュートン力学や微分方程式を熟知しています。このワン・ライナーの読者が一年後の作者など この分野に精通した方なら、下の PythonSf 式を見るだけで、この物理的な意味を、特別な解読作業をすることなく自然に読み取れるでしょう。
PythonSf ワンライナー
inV=[-0.97m`,0.243m`, 0.97m`,-0.243m`, 0m`,0m`, -0.466m`/s`,-0.432m`/s`, -0.466m`/s`,-0.432m`/s`, 0.932m`/s`,0.864m`/s`]; N=len(inV)//4; getFV=λ v,i,k:(λ r=krry(v[2k:2k+2])-krry(v[2i:2i+2]):r/norm(r)^3 if norm(r)!=0 else ~[0,0])(); sumFc=λ v,j:sum([getFV(v,j,k) for k in range(N) if j!=k]); fnc= λ *v: np.r_[v[2N:],(~[sumFc(v,j) for j in range(N)]).r]; mt=kOde(fnc,inV, 2 s`,400); pt=plotTrajectory; pt(mt[:,:2]); pt(mt[:,2:4],color=red); pt(mt[:,4:6],color=green)
このワン・ライナーは8の字軌跡だけでなく、任意の二次元三体問題に使えます。後で説明するように これを少し変形するだけで任意の三次元 N 体問題に拡張できます。
このワン・ライナーは、これだけで独立しています。Mathematica や Matlab での NoteBook とは異なり、それ以前に書かれた式に依存しません。この一行だけで完結して動作します。ですから、この一行をエディタ上で copy and paste してやり、初期条件パラメータを変更するだけで、様々の軌跡を検討できます。N 体問題についての考察を積み重ねていくとき、 このワン・ライナー・ユニットを何度も再利用できます。
逆に、このような様々に利用できるワンライナーを各分野ごとに蓄積していくことで、その分野を深く理解したことにもなります。この意味で PythonSf は数学思考をコンピュータを活用したものに変えます。今まで抽象的・思弁的な思考のだけで、写経を何度も繰り返すことで理解しなければならなかった分野であっても、コンピュータを活用して実際の問題に適用しながら理解していくことを PythonSf は可能にします。
以下では、PythonSf のワンライナーで可能な計算処理を数多く羅列していきます。以下の説明は PythonSf の計算処理機能のギャラリーともいえます。これらは PythonSf の威力を示ものになると思います。
Python での数学処理について詳しい方の中には「なぜ SAGE を使わないのか」と思う方もいると思います。理由は SAGE は数学を作る側:職業数学者のためのソフトであり、数学を使う側にとっては PythonSf の方が便利だからです。PARI/GP、GAP、Maxima、SINGULAR などの数式処理パッケージが統合されていることから SAGE が数学を作る側のソフトだと分かります。これらを必須とするような方は職業数学者だと思います。
SAGE と PythonSf は どちらも Python の数学ソフトであり Python で扱う数学については重複する部分も多くあります。大きな違いは、SAGE は 数学の定理や公式を作る側のソフトであり、PythonSf は その定理や公式を実際に応用するためのソフトだという点です。電卓の手軽さで・9割り以上をワン・ライナーで使うという点です。
Python で数学を使うことに関しては、多くの場面で SAGE より PythonSf の方が手軽です。現在 SAGE を使っているとしても、SciPy, SymPy, Matplotlib など python だけでも記述できるような対象しか扱っていない方ならば、PythonSf の方が便利です。 SAGE を使っている職業数学者の方でも、SAGE の notebook で計算させるより、Vim/Emacs など日常使っているエディタから計算させるほうが便利だと思う方が多数派でしょう。そのような方は是非とも PythonSf も試してください。御自分の定理や公式を Python で実装してあるならば、それを PythonSf でも動かして見てください。それを PythonSf のワン・ライナー式で動かすようにカスタマイズしてみてください。その学習コストもカスタマイズも一日程度のはずです。
評価版の portable な PythonSf を配布します。Python2.7 向けです。インストーラーはz使いません。このほうがユーザ環境の変更招しないので喜ばれると考えます。コンピュータにインストールするにしても、portable PythonSf のなかから、いくつかのディレクトリと py ファイルを python lib path にコピーするだけです。 また この配布には、Vim editor 上で PythonSf 式の計算を可能にするエディタ・マクロを組み込んだ Vim も一緒に配布します。
smallWithoutPython_v096a_win7_64.zip,smallWithoutPython_v096a_win_32.zip は SciPy や VPython,SymPy,Matplotlibといった PythonSf に必要なライブラリが既にインストールずみ、または別にインストールする方のために設けました。80MB と小さいサイズに収まっています。
現在のところ windows7 64ビット向けのみを用意しています。
bigIncludingPython_v096a_win7_64.zip ,bigIncludingPython_v096a_win_32は Python や SciPy,SymPy,VPython や Matplotlibといった PythonSf に必要なライブラリ全てを含んだ portable な環境です。Python でさえもインストールする必要がありません。その代償として 解凍後は 1.2GB と大きなサイズになってしまいました。でも現在の USB メモリならば問題なく持ち運べるでしょう。
現在のところ windows 向けのみを用意しています。 smallWithoutPython_v096a_win7_64 and smallWithoutPython_v096a_win_32 の違いは Vim エディタ部分だけです。Python 部分は 64/32 どちらも同じファイルです。
ここで同梱配布している Vim は kaoriya さんの windows 向けの Vim です。日本人向けの配布であり、PythonSf 式でのギリシャ文字や記号を漢字コードで表記するのにトラブルが少ないと思います。普段の思考も Vim エディタ上で行う理系の方にとって PythonSf と pysf.vim の組み合わせが life changing なソフトになることを望みます。なお PythonSf と Vim の間の問題については kVerifierLab にお問い合わせください。Kaoriya さんには無関係です。
なお PythonSf 自体は二つのファイルを除いてソースが付属しており、32/64 bit どちらでも動作します。ただしソースが付属していない pyc のみのファイルが 32/64bit で異なっています。
試用の結果 PythonSf を気に入ってもらってユーザーの Python 環境にインストールしたいとき、smallWithoutPython_v??? をお使いの方は PythonSf を働かさせのに必要な Python やライブラリをインストールずみです。そのときは下のようにしてください。
bigIncludingPython_v??? をお使いの方は下のようにしてください。
smallWithoutPython_v096_win7_64 を使っているときは、既に Python がインストールされているので、そこにディレクトリ pysf とファイル sfPP.py をコピーします。python\\Lib\site-packages\ ディレクトリの下に pysf ディレクトリは コピーします。python\\Lib\ の下に sfPP.py をコピーします。
Vc7VrfyMDdRt10D.zip ファイルは評価版の PythonSf を動かすためのキーファイルになっています。これがないと評価版の PytonSf が動作しません。コマーシャル版にアップ・グレードしたあとは必要ありません。コピーしておく必要があります。
評価版とコマーシャル版の違いは下の二点だけです。
PythonSf を気に入っていただきコマーシャル版を希望される方はカレント・ディレクトリにできている yourMichine.code ファイルを添付したメールを kverifierlab@yahoo.co.jp に送付ください。
なおコマーシャル版の価格 PythonSf は 5000 円です。
PythonSf は CUI インターフェースのソフトです。ユーザーが日常使っているエディタに組み込んで使うために、GUI 全盛の現在でも 敢えて CUI にしています。PythonSf にはエディタ組みを前提に実装されている機能が多くあります。エディタ組み込みに拘る理由は、使い込んだエディタが数式入力の human interface として最適だと考えるからです。エディタ組み込みの一例として、Vim エディタでのマクロ:pysf.vim と Emacs エディタでのマクロ pysf.el を配布しています。この章では pysf.vim マクロを組み込んだ Vim エディタ上での PythonSf の使い方を説明します。
pysf.vim マクロは PythonSf 式の計算以外にも、通常の python code, OS コマンドも Vim 上で実行させられます。C 言語などコンピュータにインストールされている任意の言語系のコンパイルや実行も可能です。これにより、ほかのアプリケーションと PythonSf を組み合わせて使うことも多くあります。
これらの pysf.vim ファイルに含まれる各マクロは 20 行にも満たないような単純で小さなマクロたちです。キーバインドなど各ユーザーで その機能を簡単に修正できます。 これらのマクロは大きく分けて「ワン・ライナー系のマクロ」、「ギリシャ文字記号入力マクロ」と「ブロック実行系のマクロ」の三つに分けられます。まずは単純なワン・ライナー系のマクロから見ていきましょう。
Portable PythonSf Vim エディタでの PythonSf のワン・ライナー式文字列をこのマクロで計算させるには、その文字列行の上にカーソルを置いてノーマル・モードで ;j 操作を行います。インサート・モード中ならば Alt+;j 操作を行います。
PythonSf ワンライナー
3+4
===============================
7
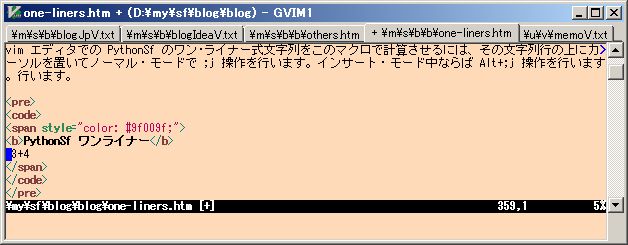
;j 操作によりカーソル下の行の 3+4 文字列を中身とする __tmp ファイルをカレント・ディレクトリに生成します。そして python -u -m sfPP -fl __tmp コマンドを OS に実行させ、CUI が返した文字列を Vim エディタの最下行のコマンド・ラインに表示します。
PythonSf Commercial 版ではなく PythonSf Open 版でワン・ライナー計算をさせたいときは、ノーマル・モードで ,j 操作を行います。
それらの計算結果を Vim エディタ編集結果として残したいときは、ノーマル・モードでの p 操作を行います。
PythonSf は Python Upper Compatible ですから、普通の Python ワンライナー・コードも ;j 操作で実行できます。Vim ノーマル・モードで、下の Python ワン・ライナー・コード文字列行の上にカーソルを持っていき ;j 操作を行えば、この Python ワンライナー・コードを実行します。
PythonSf ワンライナー
import tarfile as tr;tr.open('pycrypto-2.0.1.tar.gz', 'r').extractall()
IOError:You may use nonexistent variable name:[Errno 2] No such file or directory: 'pycrypto-2.0.1.tar.gz'
ちなみに ;j 操作で行っている Vim マクロは、下の 22 行です。
function! s:ExecPySf_1liner()
let l:strAt = s:__getLineOmittingComment()
call writefile([strAt], "__tmp")
let l:strAt = system("python -u -m sfPP -fl __tmp")
if @0 == 0
let @0 = l:strAt
else
let @0 = l:strAt
endif
let @" = @0
if match(&clipboard, "unnamed") >= 0
let @* = @0
endif
echo @0
" clipboard に unnamed が設定されてないとき、a* にも戻り値を設定する
" vim 以外のアプリケーションからも計算結果を参照できるようにするため
" 下は clipboard += unnamed になっているときにも必要です。そのときは
" p で past されるのは @* の中身だからです。
endfunction
このように小さな Vim マクロですから、このような操作が気に入らない方は、御自分に合うように簡単にカスタマイズできるはずです。
Vim macro:pysf.vim は ;j または ,j 操作で、カレント・ディレクトリに __tmp ファイルを生成します。そして python -u -m sfPP -fl __tmp または python -u -m sfPPOp -fl __tmp を OS に実行させます。すると pysf\sfPPrcssr.py または pysfOp\sfPPrcssrOp.py が実行されて __tmp ファイルをプリプロセッサ処理して、プリプロセッサ内部で実行まで行ってしまいます。その実行直前に カレント・ディレクトリにプリプロセスした結果を _tmC.py ファイルに書き出すことも行います。_tmC.py を作るのはデバッグのためです。PythonSf ワン・ライナーでエラーが起きたとき、それまでのトレース情報が欲しいときは _tmC.py ファイルを実行します。もっと詳しくデバッグしたいときは python -m pdb _tmC.py と実行します。
pysf.vim マクロはノーマル状態で、コマンド文字列の上にカーソルを置いて ;a 操作することにより OS コマンドも実行できます。下のような具合です
dir コマンド文字列 dir cl*.pvl
dir コマンドぐらいでは あまり嬉しくもないでしょうが、任意のプログラムを起動できることで多くのことが可能になります。例えば Vim 画面で下の文字列の上にカーソルを置いて ;a 操作を行えば 10 ページ目で pdf ファイルを開いてくれます。下の行を copy and paste して page パラメータ 10 と ファイル名を変えてやれば、そのページで指定された pdf ファイルを開きます。
ページ指定を伴う acrobat 起動コマンド文字列 C:"\Program Files (x86)\Adobe\Reader 9.0\Reader\AcroRd32.exe" /A page=10 D:\utl\vim73\byte_of_vim_v051.pdf
ちなみに、OS コマンドを実行させている Vim マクロ関数は Exec_command() です。興味のある方・カスタマイズしたい方は pysf.vim ファイルを参照ください。
上の pdf ファイルを開くコマンドは戻り値を必要としません。にもかかわらずコマンドの終了を待っているので、 すなわち Vim の子プロセスとしてコマンドを実行し pdf ファイルを開いているので、その pdf ファイルを開いている間は下の Vim ファイルの編集ができません。これを避けるために Windows OS では start を付けて別プロセスでコマンドを実行させます。このためにはノーマル・モードで ;f 操作を行います。
Windows では「start fileName」を実行させると fileName の拡張子に関連付けられたアプリケーションが そのファイルを引数として起動されます。これを利用するとコンピュータ操作が便利になります。たとえば Vim ノーマル・モードで URL 文字列行の上にカーソルを持っていき ;f 操作をすると、デフォルトの web ブラウザが その URL で立ち上がります。
URL の ;f すなわち start 実行 http://www.nhk.or.jp/daily/english/
PythonSf 式でグラフ表示をさせたまま別の PythonSf 式を実行させたいことが よく発生します。このときは ;s 操作を行い PythonSf を Vim とは別プロセスで実行させます。これによりグラフをさせたままで、 Vim の操作を並行して実行できます。複数個のグラフを表示さながら、別の PythonSf 式を計算させられます。
ワン・ライナー実行 Vim マクロでは、コメントは行頭から ;; までに書きます。下のような具合です。
コメント + ;; + PythonSf 式文字列 PythonSf グラフ表示式;;plotGr(sin, 0,2pi)
なぜ行頭コメントに拘るのか? PythonSf 式では # 以降にコメントを書けるのに。それはワン・ライナーが長くなると、後ろコメント文では その開始位置が一目で判読できないからです。 OS コマンド文字列や URL などの文字列が長くなるときも同じです。そのため pysf.vim の one-liner macro では 連続する二つのセミコロン ;; をデリミタとし、その前の文字列をコメントとみなします。例えば下の URL文字列行にカーソルを持っていき ;f 操作をすると NHK の英語ニュース音声をダウンロードできるページに飛んでいきます。PythonSf 式文字列行にカーソルを持っていき ;j 操作をすれば 3+4 を計算します。
コメント + ;; + URL 文字列 NHK 英語ニュース;;http://www.nhk.or.jp/nhkworld/english/radio/program/index.html コメント + ;; + PythonSf 式文字列 PythonSf 式 コメント・テスト;;3+4
PythonSf ブロック式や複数行にわたる Python コード、C プログラムなどの一般プログラム・ブロックのコンパイルや実行も pysf.vim マクロから行えます。
pysf.vim でのブロック行とは、下のように //@@ と //@@@ の文字列行で挟まれた間のテキスト行のことを意味します。pysf.vim は このブロック行に対して PythonSf ブロック式の計算をさせたり Python プログラムを実行させたり、コンパイルさせたりします。
pysf.vim でのブロック
//@@
・
ブロック行
・
//@@@
PythonSf 計算で、ワン・ライナーでの計算よりも複数行での計算のほうが望ましいときは次のようにします。
PythonSf ブロック式
//@@
# 07.11.26 beer barrel form pulley
# width = 5 meter, hieght = 1meer, depth 1 meter,
#import sf
import pysf.sfFnctns as sf
N, M =20,5
dctUpper={}
dctLower={}
for pos, index in zip(sf.masq([-2.5,N+1, 5.0/N],[-0.5,M+1, 1.0/M]), sf.mrng(N+1,M+1) ):
dctUpper[index] = (pos[0], 1, pos[1])
dctLower[index] = (pos[0],-1, pos[1])
N, M = 10,5
dctLeft ={}
dctRight ={}
for (theta, z), index in zip(sf.masq([sf.pi/2, N+1, -sf.pi/N], [-0.5, M+1, 1.0/M])
,sf.mrng(N+1,M+1) ):
dctRight[index] = [2.5+sf.cos(theta), sf.sin(theta),z]
dctLeft[index] = [-2.5-sf.cos(theta), sf.sin(theta),z]
sf.renderFaces(dctUpper)
sf.renderFaces(dctLower)
sf.renderFaces(dctLeft)
sf.renderFaces(dctRight)
dctLeft ={}
dctRight ={}
N=40
for (theta, z), index in zip(sf.masq([sf.pi, N+1, -2*sf.pi/N], [-0.5, M+1, 1.0/M])
,sf.mrng(N+1,M+1) ):
dctRight[index] = [2.5+(2-sf.cosh(z))*sf.cos(theta), (2-sf.cosh(z))*sf.sin(theta),z]
dctLeft[index] = [-2.5-(2-sf.cosh(z))*sf.cos(theta), (2-sf.cosh(z))*sf.sin(theta),z]
sf.renderFaces(dctLeft, blMeshOnly=True, meshColor=sf.red)
sf.renderFaces(dctRight, blMeshOnly=True, meshColor=sf.red)
//@@@
ちなみに、PythonSf ブロックを実行させている Vim マクロ関数は ExecSf_Bloc() です。興味のある方・カスタマイズしたい方は pysf.vim ファイルを参照ください。
なお、この PythonSf ブロック式は下のようなベルト・コンベアの 3D 図を描画しています。
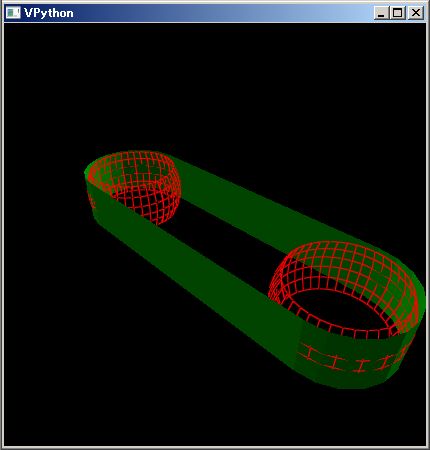
コンベヤのプーリーは上の 3D 図のように中央が膨らんでいます。直感に反すでしょうが、これによりコンベヤ・ベルトをプーリーの中央に保っています。
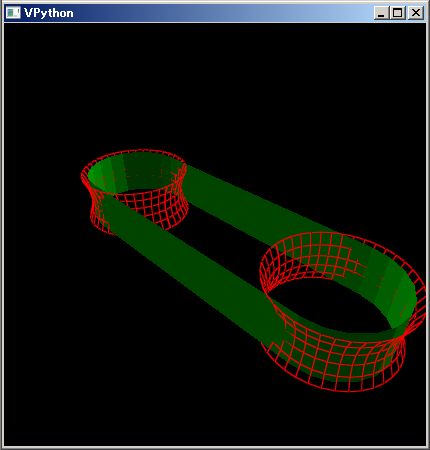
逆に下のように赤いコンベヤ・プーリーの中央を凹ませると、コンベヤ・ベルトはプーリーの端に引き寄せられ、コンベヤが壊れてしまいます。
PythonSf ブロック式
//@@
# 07.11.26
# width = 5 meter, hieght = 1meer, depth 1 meter,
#import sf
import pysf.sfFnctns as sf
N, M =20,5
dctUpper={}
dctLower={}
for pos, index in zip(sf.masq([-2.5,N+1, 5.0/N],[-0.5,M+1, 1.0/M]), sf.mrng(N+1,M+1) ):
dctUpper[index] = (pos[0], 1, pos[1])
dctLower[index] = (pos[0],-1, pos[1])
N, M = 10,5
dctLeft ={}
dctRight ={}
for (theta, z), index in zip(sf.masq([sf.pi/2, N+1, -sf.pi/N], [-0.5, M+1, 1.0/M])
,sf.mrng(N+1,M+1) ):
dctRight[index] = [2.5+sf.cos(theta), sf.sin(theta),z]
dctLeft[index] = [-2.5-sf.cos(theta), sf.sin(theta),z]
sf.renderFaces(dctUpper)
sf.renderFaces(dctLower)
sf.renderFaces(dctLeft)
sf.renderFaces(dctRight)
dctLeft ={}
dctRight ={}
N=40
for (theta, z), index in zip(sf.masq([sf.pi, N+1, -2*sf.pi/N], [-0.5, M+1, 1.0/M])
,sf.mrng(N+1,M+1) ):
dctRight[index] = [2.5+sf.cosh(z)*sf.cos(theta), sf.cosh(z)*sf.sin(theta),z]
dctLeft[index] = [-2.5-sf.cosh(z)*sf.cos(theta), sf.cosh(z)*sf.sin(theta),z]
sf.renderFaces(dctLeft, blMeshOnly=True, meshColor=sf.red)
sf.renderFaces(dctRight, blMeshOnly=True, meshColor=sf.red)
thetaS = 2.05117740593
#Z0 = 0.48121182506 # real value
Z0 = 0.35 # exagerated value
lstRear =[(2.5+sf.cosh(0.5)*sf.cos(thetaS),1,-0.5), (2.5, sf.cosh(-Z0), -Z0)]
lstFront =[(2.5+sf.cosh(0.5)*sf.cos(thetaS),1,0.5), (2.5, sf.cosh(Z0), Z0)]
N=30
for theta in sf.arSqnc(sf.pi/2, N+1, -sf.pi/N):
lstRear.append( (2.5+sf.cosh(Z0)*sf.cos(theta), sf.cosh(-Z0)*sf.sin(theta),-Z0) )
lstFront.append( (2.5+sf.cosh(Z0)*sf.cos(theta), sf.cosh(Z0)*sf.sin(theta),Z0) )
sf.plotTrajectory(lstRear, blAxis=False)
sf.plotTrajectory(lstFront, blAxis=False)
//@@@
このような曲面の組み合わさった 3D 図を word などの drawing soft を使って書くのは大変です。理系の方ならば上のような PythonSf 数式で描かせたほうが楽だと思います。如何でしょうか。
Python のプログラム・コードについても、PythonSf のブロック計算と同様に pysf.vim マクロ:Exec_BlockCntn() は //@@ と //@@@ で囲まれたブロック行を ;p で実行します。
Python ブロック実行
//@@
#from;;http://www.daniweb.com/forums/thread113274.html
#from TurtleWorld import *
#TurtleWorld()
import turtle as t
def Koch(length):
if length<=2 :
t.forward(10*length)
return
Koch(length//3)
t.left(60)
Koch(length//3)
t.right(120)
Koch(length//3)
t.left(60)
Koch(length//3)
t.setpos(-300,10)
Koch(60)
t.exitonclick()
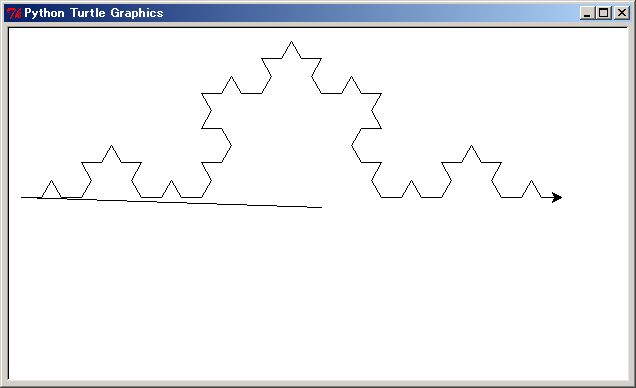
なお、PythonSf は python に upper compatible であり、上の python ブロック・コードを PythonSf 式としても実行できてしまいます。Vim エディタ上の ;k 操作でも同じプログラム動作を行ってしまいます。同じ Koch 曲線を描きます。ただし PythonSf プリプロセッサが動いてしまいます。少しだけ余分に CPU 時間を消費します。実際には体感できませんが。PythonSf 評価版では 5 秒の遅れが入るので体感できます。
ちなみに、Python ブロック実行をさせている Vim マクロ関数は ExecPy_Bloc() です。興味のある方・カスタマイズしたい方は pysf.vim ファイルを参照ください。
ブロック行に連続して書いたコマンド文字列行を実行していくことで、任意言語のコンパイル・リンク・実行をpysf.vim マクロで行わせられます。pysf.vim マクロでは ;e 操作に この動作を割り当ててあります。
Vim ノーマル・モードで //@@ ... //@@@ ブロック行の何処かにカーソルを置いて ;e 操作を行うと pysf.vim:Exec_BlockCntn() マクロは次のように働きます。
//copy ...、 //gcc .... などと // で始まるコピー・コマンドやコンパイル・コマンド文字列を書いておけば、pysf.vim はブロック行に書かれた内容をコンパイルしていきます。下に C++ プログラムでの例を示します。@@@ の次にカレント・ディレクトリの __temp ファイルを a.cpp にコピーし、a.cpp を gcc でコンパイルしています。
ブロック・コマンド連続実行: C プログラムのコンパイルと実行
//@@
//06.01.28 test valarray sum <== OK
#include &;t;valarray>
#include &;t;iostream> // iostream cannot co-exist with systemc.h
using namespace std;
int main()
{
valarray<int> vlrInAt(5); // 要素が 0 で初期化された size 5 の vararray
vlrInAt[0]=1;
vlrInAt[1]=2;
vlrInAt[2]=3;
vlrInAt[3]=4;
vlrInAt[4]=5;
cout << vlrInAt.sum() << endl;
return 0;
}
//@@@
//copy __temp a.cpp /y
//g++ a.cpp -O0 -g
//a
ブロック・コマンド連続実行 ;e キー操作では、//@@@ に連続する行に任意のコマンド文字列を記述できます。ブロック行を Haskell で実行したければ下のように書くだけです
ブロック・コマンド連続実行
//@@
data Variables = C Char | S String | I Int | Iex Integer | D Double | F Float
data VarList a = VarX a [Variables]
instance Show Variables where
show (C ch) = "C " ++ show ch
show (S str) = "S " ++ show str
show (I m) = "I " ++ show m
show (Iex n) = "Iex " ++ show n
show (D o) = "D " ++ show o
show (F p) = "F " ++ show p
instance Show a => Show (VarList a) where
show (VarX x y) = "Var " ++ show x ++ " " ++ show y
x = VarX 11 [(Iex 21), (S "fd"), (C 'a')]
main = do
print x
//@@@
//copy __temp temp.hs /y
//D:\lng\Haskell\ghc6121\bin\runghc.exe temp.hs
Var 11 [Iex 21,S "fd",C 'a']
上の Haskell 実行コマンドではフル・パスで指定しているので、path 環境変数への設定さえなしで実行しています。
このようなブロックの連続実行は小さな大量に発生する小さなテスト・プログラムの実行に便利です。小さなテスト・ファイルが何十、何百も溜まってくると、それらを管理できなくなってしまいます。でもブロック・コマンドの連続実行ならば一つのファイルのなかにテスト・コードを全部纏めて置いておけます。コンパイル・オプション、リンク・オプションやテスト実行での引数も そのファイルの同じ場所に残っています。そのブロック行の場所にカーソルを持っていくだけで、以前のテスト結果を何時でも再現できます。
ちなみにブロック・コマンドの連続実行マクロは関数は Exec_BlockCntn() です。興味のある方・カスタマイズしたい方は pysf.vim ファイルを参照ください。まだ Exec_BlockCntn() 関数はエラー処理が殆ど書かれていないので、そこらを改善すべきです。しかし この状態でも便利に使えるのでテスト的に公開します。
日本語 Windows ならば IME を使ってギリシャ文字や ∂ 記号を入力できます。でも数式入力の最中にIME のオン・オフ操作を入れることは面倒です。それを対策するために Vim の入力モードでアルファベット文字の直後で ctrl+a+g 操作をしたとき、そのアルファベットをギリシャ文字漢字に変更するマクロを作りました。
数式入力中に IME のオン・オフにイラつくかたは御利用ください。
PythonSf は CUI インターフェースのソフトです。ユーザーが日常使っているエディタに組み込んで使うために、GUI 全盛の現在でも 敢えて CUI にしています。PythonSf にはエディタ組みを前提に実装されている機能が多くあります。エディタ組み込みに拘る理由は、使い込んだエディタが数式入力の human interface として最適だと考えるからです。エディタ組み込みの一例として、Vim エディタでのマクロ:pysf.vim と Emacs エディタでのマクロ pysf.el を配布しています。この章では pysf.el マクロを組み込んだ Emacs エディタ上での PythonSf の使い方を説明します。
pysf.el マクロは PythonSf 式の計算以外にも、通常の python code, OS コマンドも Emacs 上で実行させられます。C 言語などコンピュータにインストールされている任意の言語系のコンパイルや実行も可能です。これを活用して、ほかのアプリケーションと PythonSf を組み合わせて使うことも多くあります。
これらの pysf.el ファイルに含まれる各マクロは 20 行にも満たないような単純で小さなマクロたちです。キーバインドなど各ユーザーで その機能を簡単に修正できます。 これらのマクロは大きく分けて「ワン・ライナー系のマクロ」、「ギリシャ文字記号入力マクロ」と「ブロック実行系のマクロ」の三つに分けられます。まずは単純なワン・ライナー系のマクロから見ていきましょう。
Emacs エディタで、 PythonSf のワン・ライナー式文字列を このマクロで計算させるには、その文字列行の上にカーソルを置いて C-; C-j 操作を行います。
PythonSf ワンライナー
3+4
===============================
7
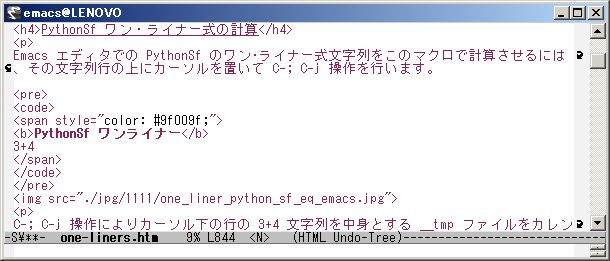
C-; C-j 操作によりカーソル下の行の 3+4 文字列を中身とする __tmp ファイルをカレント・ディレクトリに生成します。そして python -u -m sfPP -fl __tmp コマンドを OS に実行させ、CUI が返した文字列を Emacs エディタ画面下行のエコー領域に表示します。
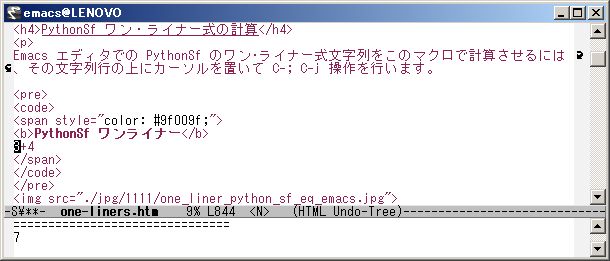
PythonSf Commercial 版ではなく PythonSf Open 版でワン・ライナー計算をさせたいときは C-, C-j 操作を行います。
それらの計算結果を Emacs エディタ編集結果として残したいときは、yank 操作を行います。
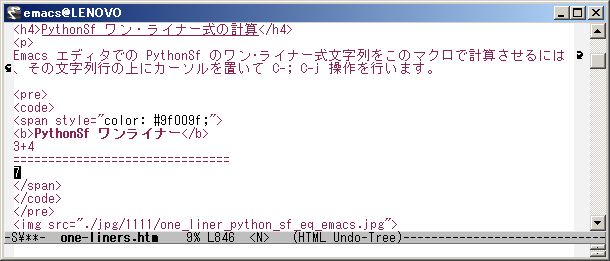
ちなみに C-; C-j 操作で行っている Emacs マクロは、下の 10 行です。
(defun ExecPySf_1liner()
"Evaluates the current line in PythonSf, then copies the result to the clipboard."
(interactive)
(write-region (__getLineOmittingComment) (line-end-position) "__tmp" nil)
(let ((strAt
(shell-command-to-string "python -u -m sfPP -fl __tmp" )
))
(message strAt)
(kill-new strAt)))
また PythonSf Open のワンライナーの計算のために C-, C-j 操作で行っている Emacs マクロは、下の 10 行です。
(defun ExecPySfOp_1liner()
"Evaluates the current line in PythonSf, then copies the result to the clipboard."
(interactive)
(write-region (__getLineOmittingComment) (line-end-position) "__tmp" nil)
(let ((strAt
(shell-command-to-string "python -u -m sfPPOp -fl __tmp" )
))
(message strAt)
(kill-new strAt)))
このように小さな Emacs マクロですから、この動作が気に入らない方は、御自分に合うように簡単にカスタマイズできるはずです。
プリプロセッサと __tmp ファイルと _tmC.py ファイルC-; C-j または C-, C-j 操作で、カレント・ディレクトリに __tmp ファイルを生成させ、python -u -m sfPP -fl __tmp または python -u -m sfPPOp -fl __tmp を OS に実行させます。すると pysf\sfPPrcssr.py または pysfOp\sfPPrcssrOp.py が実行されて __tmp ファイルをプリプロセッサ処理して、プリプロセッサ内部で実行まで行ってしまいます。同時にカレント・ディレクトリにプリプロセスした結果を _tmC.py ファイルに書き出します。_tmC.py を作るのはデバッグのためです。PythonSf ワン・ライナーでエラーが起きたとき、それまでのトレース情報が欲しいときは _tmC.py ファイルを実行します。もっと詳しくデバッグしたいときは python -m pdb _tmC.py と実行します。
PythonSf は Python Upper Compatible ですから、普通の Python Code ワンライナーも C-; C-j 操作または C-, C-j 操作で実行できます。Vim ノーマル・モードで、下の Python ワン・ライナー文字列行の上にカーソルを持っていき C-; C-j 操作を行えば、この Python Code ワンライナーを実行します。print 命令がなくても、最終式の値を PythonSf は出力するので、デバッガで行っている確認動作がエディタでもできてしまいます。
PythonSf ワンライナー
[1,2,3] == (1,2,3)
===============================
False
ちなみに上の C-; C-j 操作で行われるのは PythonSf ワンライナー式の計算であり、プリプロセスされた結果として次の Python code が実行されています。
コンソール・コマンド
type _tmC.py
from __future__ import division
# -*- encoding: cp932 -*-
from pysf.sfFnctns import *
setDctGlobals(globals())
from pysf.customize import *
if os.path.exists('./sfCrrntIni.py'):
from sfCrrntIni import *
rightSideValueGlb__= [1,2,3] == (1,2,3)
print "==============================="
print rightSideValueGlb__
putPv(rightSideValueGlb__, '_dt')
また PythonSf Open 版向けの C-, C-j 操作で実行されるのは、次の Python code です。 pysfOp ディレクトリにあるファイルで動いているのが分かります。
コンソール・コマンド
type _tmC.pyfrom __future__ import division
# -*- encoding: cp932 -*-
from pysfOp.sfFnctnsOp import *
setDctGlobals(globals())
from pysfOp.customizeOp import *
if os.path.exists('./sfCrrntIniOp.py'):
from sfCrrntIniOp import *
rightSideValueGlb__ = [1,2,3] == (1,2,3)
print "==============================="
print rightSideValueGlb__
pysf.vim マクロは OS コマンドも実行できます。 ノーマル状態で、コマンド文字列の上にカーソルを置いて C-; C-a 操作します。 下のような具合です
dir コマンド文字列
dir cl*.pvl
dir コマンドぐらいでは あまり嬉しくもないでしょうが、任意のプログラムを起動できることで多くのことが可能になります。例えば Vim 画面で下の文字列の上にカーソルを置いて C-; C-a 操作を行えば 10 ページ目で pdf ファイルを開いてくれます。下の行を copy and paste して page パラメータ 10 と ファイル名を変えてやれば、指定された 10ページで pdf ファイルを開きます。
ページ指定を伴う acrobat 起動コマンド文字列
C:"\Program Files (x86)\Adobe\Reader 11.0\Reader\AcroRd32.exe" /A page=10 D:\my\sf\ElcMg\sp330.pdf
ちなみに、OS コマンドを実行させている Emacs マクロ関数は Exec_command() です。興味のある方・カスタマイズしたい方は pysf.el ファイルを参照ください。
なお Windows7 の場合は上の操作を行うと「Adbe Reader の保護モード」のダイアログ・ウィンドウが出て「保護モードを無効にして開く」をチェックせねばなりません。でも次の節の start コマンド実行で、この面倒さも回避できます。
上の pdf ファイルを開くコマンドは戻り値を必要としません。にもかかわらずコマンドの終了を待っているので、 すなわち Emacs の子プロセスとしてコマンドを実行し pdf ファイルを開いているので、その pdf ファイルを開いている間は Emacs ファイルの編集ができません。これを避けるために Windows OS では start を付けて別プロセスでコマンドを実行させます。このためにはノーマル・モードで C-; C-f 操作を行います。
Windows では「start fileName」を実行させると fileName の拡張子に関連付けられたアプリケーションが そのファイルを引数として起動されます。これを利用するとコンピュータ操作が便利になります。たとえば URL 文字列行の上にカーソルを持っていき C-; C-f 操作をすると、デフォルトの web ブラウザが その URL で立ち上がります。
Linux では C-; C-f 操作は意味がありません。拡張子に関連付けたアプリケーションを自動起動する機能がないからです。また unix で並列にコマンドを実行させたいときは、コマンド文字列の最後に ; 文字を付け加えて C-; C-a 操作を行ってください。
URL の C-; C-f すなわち start 実行
http://www.nhk.or.jp/daily/english/

式の後ろ側のコメントは # の後に書けばよいのですが、式の前側にコメントを書きたいことがよくあります。このためにはワン・ライナー実行 Emacs マクロでは、コメントは行頭から ;; までに書きます。下のような具合です。
コメント + ;; + PythonSf 式文字列
PythonSf グラフ表示式;;plotGr(sin, 0,2pi)
なぜ行頭コメントに拘るのか? PythonSf 式では # 以降にコメントを書けるのに。それはワン・ライナーが長くなると、後ろコメント文では その開始位置が一目で判読できないからです。 OS コマンド文字列や URL などの文字列が長くなるときも同じです。そのため pysf.el の one-liner macro では 連続する二つのセミコロン ;; をデリミタとし、その前の文字列をコメントとみなします。例えば下の URL文字列行にカーソルを持っていき C-; C-f 操作をすると NHK の英語ニュース音声をダウンロードできるページに飛んでいきます。PythonSf 式文字列行にカーソルを持っていき C-; C-j 操作をすれば 3+4 を計算します。
コメント + ;; + URL 文字列
NHK 英語ニュース;;http://www.nhk.or.jp/nhkworld/english/radio/program/index.html
コメント + ;; + PythonSf 式文字列
PythonSf 式 コメント・テスト;;3+4
PythonSf ブロック式や複数行にわたる Python コード、C プログラムなどの一般プログラム・ブロックのコンパイルや実行も pysf.el マクロから行えます。
pysf.el でのブロック行とは、下のように //@@ と //@@@ の文字列行で挟まれた間のテキスト行のことを意味します。pysf.el は このブロック行に対して PythonSf ブロック式の計算をさせたり Python プログラムを実行させたり、コンパイルさせたりします。
pysf.el でのブロック
//@@
・
ブロック行
・
//@@@
PythonSf 計算で、ワン・ライナーでの計算よりも複数行での計算のほうが望ましいときは次のようにします。
PythonSf ブロック式
//@@
# 07.11.26 beer barrel form pulley
# width = 5 meter, hieght = 1meer, depth 1 meter,
#import sf
import pysf.sfFnctns as sf
N, M =20,5
dctUpper={}
dctLower={}
for pos, index in zip(sf.masq([-2.5,N+1, 5.0/N],[-0.5,M+1, 1.0/M]), sf.mrng(N+1,M+1) ):
dctUpper[index] = (pos[0], 1, pos[1])
dctLower[index] = (pos[0],-1, pos[1])
N, M = 10,5
dctLeft ={}
dctRight ={}
for (theta, z), index in zip(sf.masq([sf.pi/2, N+1, -sf.pi/N], [-0.5, M+1, 1.0/M])
,sf.mrng(N+1,M+1) ):
dctRight[index] = [2.5+sf.cos(theta), sf.sin(theta),z]
dctLeft[index] = [-2.5-sf.cos(theta), sf.sin(theta),z]
sf.renderFaces(dctUpper)
sf.renderFaces(dctLower)
sf.renderFaces(dctLeft)
sf.renderFaces(dctRight)
dctLeft ={}
dctRight ={}
N=40
for (theta, z), index in zip(sf.masq([sf.pi, N+1, -2*sf.pi/N], [-0.5, M+1, 1.0/M])
,sf.mrng(N+1,M+1) ):
dctRight[index] = [2.5+(2-sf.cosh(z))*sf.cos(theta), (2-sf.cosh(z))*sf.sin(theta),z]
dctLeft[index] = [-2.5-(2-sf.cosh(z))*sf.cos(theta), (2-sf.cosh(z))*sf.sin(theta),z]
sf.renderFaces(dctLeft, blMeshOnly=True, meshColor=sf.red)
sf.renderFaces(dctRight, blMeshOnly=True, meshColor=sf.red)
//@@@
ちなみに、PythonSf ブロックを実行させている Emacs マクロ関数は ExecSf_Bloc() です。興味のある方・カスタマイズしたい方は pysf.el ファイルを参照ください。
なお、この PythonSf ブロック式は下のようなベルト・コンベアの 3D 図を描画しています。

ちなみにコンベヤのプーリーは上の 3D 図のように中央が膨らんでいます。直感に反するでしょうが、これによりコンベヤ・ベルトをプーリーの中央に保っています。
逆に下のように赤いコンベヤ・プーリーの中央を凹ませると、コンベヤ・ベルトはプーリーの端に引き寄せられ、コンベヤが壊れてしまいます。
PythonSf ブロック式
//@@
# 07.11.26
# width = 5 meter, hieght = 1meer, depth 1 meter,
#import sf
import pysf.sfFnctns as sf
N, M =20,5
dctUpper={}
dctLower={}
for pos, index in zip(sf.masq([-2.5,N+1, 5.0/N],[-0.5,M+1, 1.0/M]), sf.mrng(N+1,M+1) ):
dctUpper[index] = (pos[0], 1, pos[1])
dctLower[index] = (pos[0],-1, pos[1])
N, M = 10,5
dctLeft ={}
dctRight ={}
for (theta, z), index in zip(sf.masq([sf.pi/2, N+1, -sf.pi/N], [-0.5, M+1, 1.0/M])
,sf.mrng(N+1,M+1) ):
dctRight[index] = [2.5+sf.cos(theta), sf.sin(theta),z]
dctLeft[index] = [-2.5-sf.cos(theta), sf.sin(theta),z]
sf.renderFaces(dctUpper)
sf.renderFaces(dctLower)
sf.renderFaces(dctLeft)
sf.renderFaces(dctRight)
dctLeft ={}
dctRight ={}
N=40
for (theta, z), index in zip(sf.masq([sf.pi, N+1, -2*sf.pi/N], [-0.5, M+1, 1.0/M])
,sf.mrng(N+1,M+1) ):
dctRight[index] = [2.5+sf.cosh(z)*sf.cos(theta), sf.cosh(z)*sf.sin(theta),z]
dctLeft[index] = [-2.5-sf.cosh(z)*sf.cos(theta), sf.cosh(z)*sf.sin(theta),z]
sf.renderFaces(dctLeft, blMeshOnly=True, meshColor=sf.red)
sf.renderFaces(dctRight, blMeshOnly=True, meshColor=sf.red)
thetaS = 2.05117740593
#Z0 = 0.48121182506 # real value
Z0 = 0.35 # exagerated value
lstRear =[(2.5+sf.cosh(0.5)*sf.cos(thetaS),1,-0.5), (2.5, sf.cosh(-Z0), -Z0)]
lstFront =[(2.5+sf.cosh(0.5)*sf.cos(thetaS),1,0.5), (2.5, sf.cosh(Z0), Z0)]
N=30
for theta in sf.arSqnc(sf.pi/2, N+1, -sf.pi/N):
lstRear.append( (2.5+sf.cosh(Z0)*sf.cos(theta), sf.cosh(-Z0)*sf.sin(theta),-Z0) )
lstFront.append( (2.5+sf.cosh(Z0)*sf.cos(theta), sf.cosh(Z0)*sf.sin(theta),Z0) )
sf.plotTrajectory(lstRear, blAxis=False)
sf.plotTrajectory(lstFront, blAxis=False)
//@@@

このような曲面の組み合わさった 3D 図を word などの drawing soft を使って書くのは大変です。理系の方ならば上のような PythonSf 数式で描かせたほうが楽だと思います。如何でしょうか。
Python のプログラム・コードについても、PythonSf のブロック計算と同様に pysf.el マクロ:ExecPy_Block() は //@@ と //@@@ で囲まれたブロック行を C-; C-p で実行します。
Python ブロック実行
//@@
#from;;http://www.daniweb.com/forums/thread113274.html
#from TurtleWorld import *
#TurtleWorld()
import turtle as t
def Koch(length):
if length<=2 :
t.forward(10*length)
return
Koch(length//3)
t.left(60)
Koch(length//3)
t.right(120)
Koch(length//3)
t.left(60)
Koch(length//3)
t.setpos(-300,10)
Koch(60)
t.exitonclick()

なお PythonSf は python に upper compatible であり、上の python ブロック・コードを PythonSf 式としても実行できてしまいます。Emacs エディタ上の C-; C-k 操作でも同じプログラム動作を行ってしまいます。同じ Koch 曲線を描きます。ただし PythonSf プリプロセッサが動いてしまいます。少しだけ余分に CPU 時間を消費します。実際には体感できませんが。PythonSf Commercial 版では 5 秒の遅れが入るので体感できます。
ちなみに、Python コードのブロック実行をさせている Emacs マクロ関数は ExecPy_Bloc() です。興味のある方・カスタマイズしたい方は pysf.el ファイルを参照ください。
ブロック行の後に連続して書いたコマンド文字列行を実行していくことで、任意言語のコンパイル・リンク・実行をpysf.el マクロと C-; C-e 操作で行わせたいのですが、pysf.el マクロでは実装できていません。Vim マクロでは実装できているのですが。
漢字入力機能:IME を使ってギリシャ文字や ∂ 記号を入力できます。でも数式入力の最中にIME のオン・オフ操作を入れることは面倒です。それを対策するために、アルファベット文字の直後で C-, C-g 操作をしたとき、そのアルファベットをギリシャ文字漢字に変更するマクロを作りました。
数式入力中に IME のオン・オフにイラつくかたは御利用ください。
全てのソース・コードを但し書き付き修正 MIT ライセンスで公開している PythonSf の Open 版も設けています。 PythonSf 商用版よりプロプロセッサが大幅に簡易化されています。そのため PythonSf 商用版でのような簡潔な数式記述ができなくなっています。でも Python 文法の範囲内で記述している分には PythonSf 商用版/Open 版は同じとみなせます。
PythonSf Open のプリプロセッサが大幅に簡易化されているといっても、ギリシャ文字や∂∇□△の漢字記号は扱えます。`:backquote による名前空間の拡張も扱えます。できないのは積演算子の省略や 行列・ベクトルの ~[...] 表記です。またべき乗演算子に ^ 記号を使えません。** 記号を使わねばなりません。これらは「日常のメモ書き数式のままで計算する」という PythonSf の目的からは後退しています。でも Python 文法での記述に戻るだけであり、耐えられる範囲の制限だと思います。
現在:2013年6月 で PythonSf Commercial の 70% 程度の機能が PythonSf Open 版に移植されています。Open 版に移植されていない機能を使うときは Commercial 版で計算してください。";j" 操作が必要になることと 5 秒ディレーが入るだけです。
なお但し書き付き修正 MIT ライセンスの但し書き条件は
なお但し書きの内容は
PythonSf Open が Commercial 版より大きく劣るのは積演算子の省略が使えないことです。また ClTensor クラスではなく np.ndarray を使うため、行列の積、ベクトルの内積に np.dot(..) 関数を使わねばなりません。以下のような具合です
# パウリ行列 σx に対するベクトル a=[2,3] の期待値の計算例
PythonSf Commercial one-liner
a=[2,3]; a `σx a
===============================
12.0
PythonSf Open one-liner
a=[2,3]; np.dot(a, np.dot(`σx, a))
===============================
12.0
# PythonSf Open では `σx が np.ndarray のため、a*`σx*a が期待値ではなく、要素ごとの積行列になってしまう
# また積演算子の省略ができないので明示的に * 演算記号を記述せねばならない。
PythonSf Open miss calculation
a=[2,3]; a*`σx*a
===============================
[[ 0. 9.]
[ 4. 0.]]
積演算子を省略できないこと、np.dot(..) を使うことは数式の可読性・記述性を著しく落とします。といっても Python のレベルに落ちるだけですが。
numpy matrixnumpy の行列を matlab での行列演算操作に近づけるものとして np.matrix があります。でも np.matrix は実質的に使い物になりません。計算結果を出力させても、見た目では np.ndarray か np.matrix か分からないからです。同時に numpy/scipy に定義されている関数は ufunc でないものも多いからです。ufunc(np.matrix) と ufunc 関数を呼び出すのならば、その戻り値も np.matrix です。でみ non-ufunc(np.matrix) は np.ndarray になってしまうからです。np.matrix を使うならば、使う関数の全てについて ufunc であるか否かが頭に入っていなければならなりません。そうでないと予期しない np.matrix と np.ndarray の混在計算になってしまいます。分けが分からなくなります。それぐらいならば np.ndarray だけに限って計算したほうが楽です。
np.matrix の実装は中途半端であり、PythonSf では np.matrix を使わないことを推奨します。PythonSf Open では np.ndarray(..) の範囲で閉じるようにます。PythonSf Open でもユーザーが明示的に np.matrix(..) を使うことは可能です。でも そのときはユーザーが np.matrix と np.ndarray の違いを管理せねばなりません。
numpy ndarray と ClTensor/ClFldTnsPythonSf Commercial 版では、中途半端な np.matrix の代わりに ClTensor/ClFldTns クラスを使っています。
PythonSf Commercial, Open, Python の機能比較表を下に示します。
| ・ | PythonSf Commercial | PythonSf Open | Python |
|---|---|---|---|
| 漢字ギリシャ文字・∇□∂△記号の使用 | 可能 | 可能 | 不可 |
| ` による名前空間の拡張 | 可能 | 可能 | 不可 |
| ユーザー定義演算子:~==,~*, ... | 可能 | 不可 | 不可 |
| default import ファイル | customize.py/sfCrrntIni.py | customizeOp.py/sfCrrntIniOp.py | 無理 |
| 積演算子の省略 | r=5; 2pi r | r=5; 2*pi * r | r,pi=5,3.14; 2*pi * r |
| べき乗記号 | ^ or ** | ** | ** |
| 計算結果のファイル変数 _dt.pvl 生成 | 生成する | 生成しない | 生成しない |
| 複素数表記 | a,b=1,2; a + b `i | a,b=1,2; a + b*`i | a,b=1,2; a + b*1j |
| 多項式関数 | `X^2+3`X+1 | `X**2+3*`X+1 | lambda x:x**2+3*x+1 |
| 行列・ベクタ生成 | ~[1,2,3] | kry0(1,2,3) | np.array([1,2,3]) |
| Zp(3)要素のベクタ生成 | ~[1,2, Z3] | kry0(1,2, Z3) | np.array([1,2], dtype=Z3) |
| 行列・ベクタ積 | `σx [1,2] | np.dot(`σx, [1,2]) | np.dot([[0,1],[1,0]], [1,2]) |
| ベクタ内積 | a,b=~[1,2],[3,4]; a b | a,b=[1,2],[3,4]; np.dot(a,b) | a,b=[1,2],[3,4]; np.dot(a,b) |
| 逆行列 | 1/~[[1,2],[3,4]] | np.linalg.inv([[1,2],[3,4]]) | np.linalg.inv([[1,2],[3,4]]) |
| Zp(3)要素行列の逆元 | 1/~[[1,2],[3,4], Z3] | 不可 | 不可 |
| ベクトル関数 | ~[`X^2,`Y+1] | λ x,y:kryO(x**2,y+1) | lambda x,y:np.array([x**2,y+1]) |
PythonSf Open 版は全てのコードを但し書き付き MIT ライセンスで公開しています。ただ Open 版のプリプロセッサ pysfOp/sfPPrcssrOp.py が 160 行と小さいため、積演算子の省略やユーザー演算子拡張機能が使えません。でも漢字ギリシャ文字 ∇□∂△ 記号は使えます。Backqote:` による名前空間の拡張も可能です。 文法としては Python ⊂ PythonSf Open ⊂ PythonSf Commercial の関係にあるので、Python 文法の範囲内で数式を記述している分には PythonSf Open 版でも問題ありません。
PythonSf Open 版には上のような制限が付きますが、十分に実用的な段階にあるとも言えます。以下の説明では PythonSf Commercial 版に限って説明しています。PythonSf Open 版で使うときは上の書き換えを行ってください。それでも動かないときは Commercial 版を使用してください。5 秒のディレーが入るだけです。
なお 2013.07.09 現在 PythonSf Open 版の block 実行はバギーです。漢字ギリシャ文字を使えません。でも多用するワン・ライナーは十分に実用的なレベルにあります。
行列・ベクトルの生成には kryO(..) 関数を使うPythonSf Open 版では、行列・ベクトルの生成には kryO(..) 関数を使うことを推奨します。Numpy の np.array(..) 関数も使えるのですが、np.array(..) は int 引数値のとき、整数タイプの行列やベクトルを生成してしまいます。この整数タイプの行列やベクトルに浮動小数点値を代入すると、小数点以下が Warning や Error なしで切り捨てられてしまいます。
多くの場合は PythonSf 式を書いている段階で気づくのですが、どうしても見逃しが発生します。数学では整数型変数への浮動小数点の代入と言う考え方がないからです。見逃しても小数点以下の切捨てだけですから、計算結果は一見正しそうな値となっています。
演習問題で一つの式を解くだけならば、小さな見逃しにすぎません。でも論文や実務で多くの数式・計算が積み重ねられ、そのなかの少ない箇所で小数点以下が切り捨てられる問題が入り込むと厄介です。後で結果が変だと気付いても、その原因箇所の特定が大変です。その特定作業だけで一週間とられたりします。それが数ヶ月に一回程度の頻度で発生することになりかねません。
kryO(..) 関数による行列・ベクトルの生成ならば整数引数でも浮動小数点タイプの行列・ベクトルを生成します。明示的に int を指定したときだけ整数タイプの行列ベクトルを生成します。
整数引数での kryO(..) 関数による浮動小数点ベクトルの生成 kryO(1,2,3) =============================== [ 1. 2. 3.] int タイプ指定での kryO(..) 関数による浮動小数点ベクトルの生成 kryO(1,2,3, int) =============================== [1 2 3] np.array での default int ベクトル vc = np.array([1,2,3]); vc =============================== [1 2 3] np.array int ベクトルでの小数点の切捨て vc = np.array([1,2,3]); vc[0]=2.6; vc =============================== [2 2 3]
PythonSf は数式記述を簡便なメモ書き数式に近づけるためプリプロセッサを介在させ、 少しだけ Python 文法を拡張しています。この拡張部分を知っておかないと、PythonSf 数式を見ても意味が分らない部分が出てくると思います。PythonSf が始めての方は、この節だけは目を通しておかれたほうが理解が早いと思います。
数学の式では積の演算子が省略されることが普通です。PythonSf でも それを踏襲します。
PythonSf は普段メモ書きしている数式に近い記述で計算処理することを目指して作りました。このためにプリプロセッサを介在させています。このプリプロセッサにより積演算子の省略を可能にしています。下のような具合です。
PythonSf ワンライナーたち
a,b=3,4; 2 a b
===============================
24
a,b=3,4; 2a + 3b
===============================
18
a,b=3,4; 2(a+b)
===============================
14
a,b=3,4; a (a+b)
===============================
21
積演算子の省略を誤用したPythonSf ワンライナーたち
a,b=3,4; ab
name 'ab' is not defined at excecuting:ab
a,b=3,4; a(a+b)
'int' object is not callable at excecuting:a(a+b)
ただし Python 文法との共存を許すため、 ab とか a(a+b) のようには書けません。Python 文法では ab 文字列は a*b ではなく、変数 ab とみなすからです。また a(a+b) は、 a と (a+b) の積ではなく、引数 a+b を関数 a により関数呼び出しする意味になるからてす。
数学ではべき乗演算子に ^ を使うことが普通です。** 演算子を使うのはログラミングの世界での話です。一方で Python では ^ は bit exor 演算子の意味になります。
PythonSf プリプロセッサでは Python との互換性よりも、数学記述に近いメモ書き数式のほうを選択し ^ をべき乗演算子の意味にしました。bit exor 演算を行せるときは \^ を使うことにしました。もちろん ** 演算子をべき乗の意味に使うことも可能です。下のような具合です
PythonSf ワンライナー
2^4, 2\^4, 2**4
===============================
(16, 6, 16)
PythonSf 式は Python Upper Compatible だといっていますが、ここの ^ 演算子のように、厳密には Python Upper Compatible ではない箇所が幾つかあります。Python では sin (pi/3) とスペースを挿入しても sin 関数を計算をしてくれますが、PythonSf 式では sin*(pi/3) の意味になってしまいます。でも bit exor 演算など殆どの方は一年に何回も使わないはすです。関数呼び出しの括弧の前にスペースを必要とする方もいないと思います。このような些細なことがらだけを例外とするならば「PythonSf は Python Upper Compatible だ」といっても許されると主張します。
数式の記述は、できるだけ短く書けることが望まれます。数学では x,y が何であるかを説明しなくても x+y と書いたら、二変数の足し算すなわち二変数関数のことを意味します。でもプログラミングの世界でそんなことをしたら「未定義の x,y を使っている」エラーとなって動きません。
グローバルな x,y ラベルに何らかのインスタンスを予めアサインしておけば未定義エラーを避けられます。でも x,y のような短い変数名をグローバルな定義済みにすることは Python コードに悪影響を与えてしまいます。
PythonSf では、この数式と Python コードの衝突を回避するために、変数名の前後に複数のバック・クォートを追加できるようにしました。このように名前空間を拡張することで、既存の Python コードにはない、数学向けの短い変数名を使用できるようにしました。
たとえば `X に加減乗除べき乗算が可能な恒等関数クラスの callable instance を割り当てておくことで `X^2+3`X+1 を二次関数として扱えるようにしています。下のような具合です。
PythonSf ワンライナーたち
(`X^2+3`X+1)(1)
===============================
5
(`X^2+3`X+1)(2)
===============================
11
x=`X; (x^2+3x+1)(3)
===============================
19
`Y に、引数の二番目を取り出す機能を追加した加減乗除べき乗算が可能な恒等関数クラスの callable instance を割り当てておくことで `X^2+3`Y を二変数の二次関数として扱えるようにしています。下のような具合です。
PythonSf ワンライナーたち
(`X^2+3`Y+1)(1,2)
===============================
8
sqrt(`X^2+3`Y+1)(1,2)
===============================
2.82842712475
PythonSf では、ベクトルや行列をあらわすのに ~[...]の記法を使います。下のような具合です。
PythonSf ワンライナーたち
~[1,2,3] # float value vector
===============================
[ 1. 2. 3.]
---- ClTensor ----
~[1,2,3+4j] # complex value vector
===============================
[ 1.+0.j 2.+0.j 3.+4.j]
---- ClTensor ----
vc=~[1,2,3]; vc+[4,5,6] # vector add
===============================
[ 5. 7. 9.]
---- ClTensor ----
vc=~[1,2,3]; vc [4,5,6] # vector inner product
===============================
32.0
~[ [1,2],[3,4] ] # matrix
===============================
[[ 1. 2.]
[ 3. 4.]]
---- ClTensor ----
mt,vc=~[[1,2],[3,4]],~[5,6]; mt vc # product of matrix and vector
===============================
[ 17. 39.]
---- ClTensor ----
mt=~[[1,2],[3,4]]; 1/mt, mt^-1 # inverse of matrix
===============================
(ClTensor([[-2. , 1. ],
[ 1.5, -0.5]]),
ClTensor([[-2. , 1. ],
[ 1.5, -0.5]]))
# 辞書行列から ClTensor 行列の生成
dct={(0,0):1,(0,1):2,(1,0):3,(1,1):1}; ~[dct]
===============================
[[ 1. 2.]
[ 3. 1.]]
---- ClTensor ----
PythonSf のベクトルや行列ではデフォルトで浮動小数点型のそれにします。浮動小数点のベクトルや行列であっても整数のベクトル・行列であっても、整数のときと同様な計算結果になることが多いからです。逆に整数は割り算が入ると小数点以下が 0 になってしまうからです。
ベクトルや行列に整数など浮動小数点以外の型:typeを指定したいときは ~[..., type] と最後に型:type引数を追加します。
PythonSf ワンライナー
~[1,2,3, int] # int type vector
==============================
[1 2 3]
---- ClTensor ----
oc.BF:ブール体型などユーザーが定義する型を指定することで、その型でのベクトル・行列演算も可能です。
PythonSf ワンライナーたち
~[1,0,1, oc.BF] # oc.BF:Bool Field type vector
===============================
[1 0 1]
---- ClFldTns:<class 'pysf.octn.BF'> ----
mt,vc=~[[1,1,0],[1,1,1],oc.BF],~[1,0,1, oc.BF]; mt vc # product of Bool Type matrix and vector
===============================
[1 0]
---- ClFldTns:<class 'pysf.octn.BF'> ----
~[1,2,3, oc.BF] # oc.BF:Bool Field type vector
===============================
[1 0 1]
---- ClFldTns:< class 'pysf.octn.BF'> ----
class Cl(int):pass; ~[1,2,3, Cl] # user defined type
===============================
[1 2 3]
---- ClFldTns:&;t;class 'pysf.sfPPrcssr.Cl'> ----
PythonSf の ~[...] シンタックスによる行列やベクトルの生成では ClTensor または ClFldTns インスタンスを生成します。Numpy の ndarray インスタンスではありません。ベクトル行列の乗除算でも整数や実数のときと同様なシンタックスで記述するためです。ですから ClTensor や ClFldTns の乗算は、「行列とベクトル」「行列と行列」の乗算になります。「ベクトルとベクトル」の乗算は内積となり除算はエラーになります。一方で ndarray の乗除算は要素ごとの乗除算です。最初のうちは戸惑うと思います。御注意ください。
PythonSf ワンライナーたち
# PythonSf でのベクトルどうしの積:内積
~[1,2,3] ~[4,5,6]
===============================
32.0
~[1,2,3]/ ~[4,5,6]
Traceback (most recent call last):
File "D:\lng\Python26\lib\runpy.py", line 122, in _run_module_as_main
"__main__", fname, loader, pkg_name)
File "D:\lng\Python26\lib\runpy.py", line 34, in _run_code
exec code in run_globals
File "D:\my\vc7\mtCm\sfPP.py", line 2, in
pysf.sfPPrcssr.start()
File "pysf\sfPPrcssr.py", line 2722, in start
__execLine( (" ".join(sys.argv[1:])).strip() )
File "pysf\sfPPrcssr.py", line 2345, in __execLine
valStt = eval(ustConvertedAt, globals(), locals() )
File "", line 1, in
File "pysf\sfFnctns.py", line 547, in __truediv__
return self.__mul__(ag.inv())
File "pysf\sfFnctns.py", line 492, in inv
return copy.deepcopy(self.m_inv)
File "pysf\sfFnctns.py", line 909, in __getattr__
self.__dict__['m_inv'] = ClTensor(sl.inv(self))
File "D:\lng\Python26\lib\site-packages\numpy\linalg\linalg.py", line 423, in inv
return wrap(solve(a, identity(a.shape[0], dtype=a.dtype)))
File "D:\lng\Python26\lib\site-packages\numpy\linalg\linalg.py", line 290, in solve
_assertRank2(a, b)
File "D:\lng\Python26\lib\site-packages\numpy\linalg\linalg.py", line 134, in _assertRank2
two-dimensional' % len(a.shape)
numpy.linalg.linalg.LinAlgError: 1-dimensional array given. Array must be two-dimensional
# Numpy での割り算:ベクトル要素どうしの積
vA,vB = np.array([1,2,3]),np.array([4,5,6]); vA/vB
===============================
[ 0.25 0.4 0.5 ]
# Numpy でのベクトル要素どうしの積
np.array([1,2,3]) np.array([4,5,6])
===============================
[ 4 10 18]
np.array([1,2,3])/np.array([4,5,6])
===============================
[ 0.25 0.4 0.5 ]
なお、整数/実数/複素数を要素とする ClTensor インスタンスが最終計算値のとき、計算結果の文字列の最後に ---- ClTensor ---- 文字列が追加されます。ClFldTns インスタンスが最終計算値のときは ---- ClFldTns:< class 'pysf.octn.BF'> ---- など要素のタイプも含めた文字列が返されます。下のような具合です。np.ndarray インスタンスのときはタイプ情報は返されません。
ClTensor インスタンスのベクトル・行列の式
===============================
戻り値
---- ClTensor ----
ClFldTns インスタンスのベクトル・行列の式
===============================
戻り値
---- ClFldTns:< class 'pysf.octn.BF'> ----
np.ndarray インスタンスのベクトル・行列の式
===============================
戻り値
# 型情報の明示的な表示はありません。
PythonSf ワンライナーたち
σx,σz=~[[0,1],[1,0]], ~[[1,0],[0,-1]]; σx σz
===============================
[[ 0. -1.]
[ 1. 0.]]
---- ClTensor ----
σx,σz=~[[0,1],[1,0]], ~[[1,0],[0,-1]]; σx+σz
===============================
[[ 1. 1.]
[ 1. -1.]]
---- ClTensor ----
ギリシャ文字の他に日常の計算で使うことの多い「∇□∂△」漢字記号も扱えるようにしています。特に微分記号 ∂ は便利に多用されます。
PythonSf ワンライナーたち
# 数値微分
∂x(`X^2+2`X+3)(2)
===============================
6.0
# シンボリック微分
ts(); ∂x(`x^2+2`x `y+3)
===============================
2*x + 2*y
# Jacobian 数値微分
∂J(`X^2+`Y^2, 2)(1,2)
===============================
[ 2. 4.]
---- ClTensor ----
ワンライナーで lambda 式が多用されることと、lambda より漢字 λ の方が視認性で勝ることより、lambda 式の記述に漢字 λ を使えるようにしています。これによりコンピュータ・サイエンスの教科書にあるような λ 式記述が可能になります。下のような具合です。その代償として λ 一文字だけの変数を使えなくなります。
PythonSf ワンライナーたち
f=λ x:sin(x)+2cos(x); f(pi/2)
===============================
1.0
# python lambda 式でデフォルト引数を利用した let 文 を使う
# デフォルト引数 y=sin(x)+2cos(x) が let 分になっている。
# y の書き換えができない。
f=λ x:(λ y=sin(x)+2cos(x): y+y^2)(); f(pi/2)
===============================
2.0
# λ ラベルには値を割り振れません。λ は lambda 構文だからです。
λ=3; 2λ
invalid syntax (, line 1) at excecuting:lambda=3
Python での λ:labmda 式は、コンピュータ・サイエンスでの λ式 に近い仕様になっています。下の様に Church 数による自然数のモデル化ができてしまいます。
PythonSf ワンライナーたち
# Charch 数 2
Z='1';S =λ s:s+'1';(λ s:λ z:s(s(z)))(S)(Z)
===============================
111
# Charch 数での 2 + 3
Z='1';S =λ s:s+'1';(λ s:λ z:s(s( s(s(s(z))) )))(S)(Z)
===============================
111111
λ式にラベルをアサインすることで、リカーシブな関数呼び出しが可能になります。これにより短いコードで複雑な処理を可能にできることが多くあります。
PythonSf ワンライナーたち
# gcd 関数:Euclid 互助法
gcd=λ a,b: b if a%b==0 else gcd(b, a%b); gcd(12,9)
===============================
3
gcd=λ a,b: b if a%b==0 else gcd(b, a%b); gcd(9,12)
===============================
3
# lcm 関数
gcd=λ a,b: b if a%b==0 else gcd(b, a%b); lcm=λ a,b:a*b//gcd(a,b); lcm(3,4)
===============================
12
~~, ~^, ~+, ~-, ~*, ~/, ~%, ~&, ~|, ~== の中置ユーザー演算子を定義できます。ただ現在のところ演算子の優先順位が最大固定なので、括弧が必要になることか多くなります。
例えば ~== に nearlyEq(..) 関数を customize.py の中で割り振ってあります。ですから下のような計算ができます。
PythonSf ワンライナーたち
(3.3pF`) ~== (3.300001pF`)
===============================
True
(3.3pF`) ~== (3.30001pF`)
===============================
False
~[1, 2] ~== [1, 2.000001]
===============================
True
~[1, 2] ~== [1, 2.00001]
===============================
False
PythonSf プリプロセッサが PythonSf 式を実行する前に from pysf.sfFnctns import * を行っています。これにより基本数値関数 exp, sin, cos, tan, sinh, cosh, tanh, arcsin, arccos, arctan, log, log10, sqrt など多くの基本的な数学要素をグローバル名前空間に導入済みにしています。これにより import math などを行わずに計算処理が可能です。通常の関数電卓で行う計算の殆どを PythonSf では import なしで可能です。
PythonSf ワンライナー
tan(pi/3)
===============================
1.73205080757
すでに `X などの変数名を使っていますが、PythonSf では変数名の前後に back quote:` を複数追加したものを、プリプロセッサによる変換を介在させることで許しています。この名前空間の拡張と PythonSf のカスタマイズ機能により、数学慣習に従った短い数式記述と Python 文法を共存させています。
より具体的に見てみましょう。PythonSf プリプロセッサが ` で始まる変数名を見つけると k__bq_ を文字列の最初に、__ を文字列の最後に付加した物に変換します。例えば `X は k__bq_X__ 文字列に変換されます。そしてカスタマイズ・ファイル:customize.py の中で k__bq_X__ 変数名に加減乗除べき乗算が可能な恒等関数のクラス・インスタンスを assign することで `X^2+1 などの記述を可能にしています。
数式の記述は、できるだけコンパクトであることが望まれます。そのため多くの暗黙の前提の上に数式が書かれます。数学の世界では x と書けば、未知変数 x を意味します。物理の世界では h や c 等を書いたときには、プランク定数と光速度の積を意味したりします。でも X,h,c のように短いグローバル変数ラベルに、恒等関数、プランク定数や光速度の意味を与えてしまうのは、Python コードの記述としては やりすぎです。どこかで Python コードと矛盾する可能性が出てきます。
この問題を対策するため、PythonSf では変数文字列の前後に一つ以上のバック・クォート文字を追加できるようにして名前空間を拡張しました。この拡張された変数名 の拡張された変数名 `X や h` や c` にプランク定数や光定数を割り当てることで、数学や物理での暗黙の前提を使いながらも Python コードと矛盾しないメモ書き数式記述を可能にしました。
なお PythonSf では名前の最後にバック・クォートを追加した変数名には物理単位、または物理定数を割り当てるという naming convention を適用しています。
また back quote は Γ``_[i,j,k] などのようにテンソル・インデックスの上下を示すことにも naming convention として使います。この例では i,j が上側の, k が下側のインデックスになります。Γ``_ では back quate が名前の前後ではないと指摘されるかもしれません。厳密には名前の前後というとき under_score 文字列は含まないと思ってください。
数式を書くとき、暗黙の前提とする事柄はユーザーの専門分野によって異なります。場合によっては計算するディレクトリごとに暗黙の前提が必異なったりさえします。
このため、PythonSf では共通前提向けに pysf\customize.py ファイルを設けています。それとは別に、カレント・ディレクトリに sfCrrntIni.py ファイルを置けるようにしています。PythonSf プリプロセッサは計算処理の前に from pysf.customize import * を実行します。カレント・ディレクトリに sfCrrntIni.py ファイルが存在するときは、from sfCrrntIni import * も実行します。
標準配布の中に customize.py, sfCrrntIni.py も含まれています。customize.py の中で上の PythonSf 式例で使った物理単位や `X,`x 変数を定義しています。その他に、単位純虚数:`i, ブール値:`1,`0、パウリ行列:`σx,`σy,`σz を、ts() 関数の中では有理数の 1:`1r などを customize.py で定義しています。次のような計算が可能です。
PythonSf ワンライナー
exp(2pi `i/3)
===============================
(-0.5+0.866025403784j)
# oc.BF Bool 値ベクトルの和
~[`1,`0,`1]+[`1,`1,`1]
===============================
[0 1 0]
---- ClFldTns:< class 'pysf.octn.BF'> ----
`σx + 2`σy
===============================
[[ 0.+0.j 1.-2.j]
[ 1.+2.j 0.+0.j]]
---- ClTensor ----
# exp 行列の計算
t,mt=0.1, `σx + 2`σy; expm(`i t mt)
===============================
[[ 0.97510399+0.j 0.19833750+0.09916875j]
[-0.19833750+0.09916875j 0.97510399+0.j ]]
---- ClTensor ----
# 有理数の数列
ts(); [`1r/(k+1) for k in range(10)]
===============================
[1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 1/9, 1/10]
ts(); sum( [`1r/(k+1) for k in range(10)] )
===============================
7381/2520
その他 customize.py には三階の Livi-Civita テンソル:`εL, 微分関数:∂x, Jacovian 微分:∂J、Laplace 演算子多項式:`s などが定義してあり、これらを使った計算処理が可能です。下のような具合です。
PythonSf ワンライナーたち
`εL # Levi-Civita tensor
===============================
[[[ 0. 0. 0.]
[ 0. 0. 1.]
[ 0. -1. 0.]]
[[ 0. 0. -1.]
[ 0. 0. 0.]
[ 1. 0. 0.]]
[[ 0. 1. 0.]
[-1. 0. 0.]
[ 0. 0. 0.]]]
---- ClTensor ----
===============================
[-3. 6. -3.]
---- ClTensor ----
a,b=~[1,2,3],~[4,5,6]; np.cross(a,b) # outer product by Numpy
===============================
[-3. 6. -3.]
∂x(`X^2+1)(1) # differential value of x^2+1 at 1
===============================
2.0
∂J(~[`X+`Y, `X `Y], 2)(1,2) # Jacobian of ~[x+y,x y] field at [1,2]
===============================
[[ 1. 1.]
[ 2. 1.]]
---- ClTensor ----
1/(`s+1) ( (`s+2) +1/(`s+3)) # calculate Laplace operator expression
===============================
2
1 s + 5 s + 7
-------------
2
s + 4 s + 3
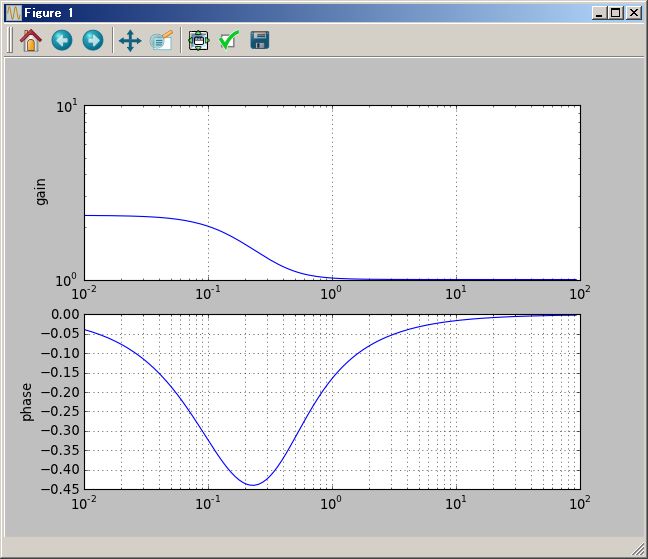
# Bode 線図
(1/(`s+1) ( (`s+2) +1/(`s+3))).plotBode(0.01Hz`,100Hz`)
標準配布の PythonSf では sfCrrntIni.py の中で、整数剰余体:Zp(N) の N が 2,3,4,5,7 のときの Z2,Z3,Z4,Z5,Z7 を定義しています。これらは PythonSf 式を実行するときのグローバル変数中に存在することとなり、import 文無しで PythonSf 式中で Z2,Z3,Z4,Z5,Z7 を好きに使えます。次のような具合です。
PythonSf ワンライナーたち
# Z3 行列
~[range(2*2), Z3].reshape(2,2)
===============================
[[Z3(0) Z3(1)]
[Z3(2) Z3(0)]]
---- ClFldTns:< class 'sfCrrntIni.Z3'> ----
# Z3 行列の逆行列
mt=~[range(2*2), Z3].reshape(2,2); mt^-1
===============================
[[Z3(0) Z3(2)]
[Z3(1) Z3(0)]]
---- ClFldTns:< class 'sfCrrntIni.Z3'> ----
# Z3 行列どうしの積
mt=~[range(2*2), Z3].reshape(2,2); mt mt^-1
===============================
[[Z3(1) Z3(0)]
[Z3(0) Z3(1)]]
---- ClFldTns:< class 'sfCrrntIni.Z3'> ----
customize.py/sfCrrntIni.py はユーザーが自分の都合に合わせてカスタマイズして使うものです。中身は Python プログラムに過ぎませんので、ユーザの必要に応じて自由に改変できます。
下の rpy2 を使えば下の Python プログラムで R に計算させられます。(ここのコードを使わせてもらいました。)
Python コード・ブロック
//@@
import rpy2.robjects as robjects
rmean = robjects.r('mean')
rvar = robjects.r('var')
tmp_vec = [1.1,3.3,5.5]
vec = robjects.FloatVector(tmp_vec)
mean = rmean(vec)[0]
var = rvar(vec)[0]
//@@@
ならば下のコードを sfCrrntIni.py に追加してやることで、エディタから R の機能が使えるようになります。
Python コード・ブロック
import rpy2.robjects as robjects
ro=robjects.r
rof=robjects.FloatVector
//@@
//@@@
上の R-Python 計算を次の PythonSf ワン・ライナーで計算できてしまいます。
PythonSf ワンライナー
vc = [1.1,3.3,5.5]; rmean,rvar = ro('mean'), ro('var'); vec = rof(vc); rmean(vec)[0], rvar(vec)[0]
もっとも平均や分散を求めるだけならば、下の PythonSf ワン・ライナーの方を勧めます。多くの統計計算も scipy.stats sub package の物で済むと思います。
PythonSf ワンライナー
vc = [1.1,3.3,5.5]; np.mean(vc), np.cov(vc)
===============================
(3.3000000000000003, array(4.84))
PythonSf では、pickable なインスタンスをファイル変数にできます。このファイル変数はカレント・ディレクトリに拡張子 pvl で実際のファイルとして作られます。OOP 用語を使って言い換えると、pickable な計算結果をファイル変数としてシリアライズして、何時でも再利用可能にします。one-liner では「:=」でファイル変数への書き込みを行い「=:」でファイル変数からの読み込みを行います。ファイル変数はカスタマイズと似た機能を果たします。
下に示すように「tmp:=3+4」で tmp.pvl ファイルがカレント・ディレクトリに作られます。「=:tmp; tmp/2」でカレント・ディレクトリから tmp.pvl を読み出し、tmp 変数に その値を設定します。そのあと tmp を含んだ式を計算できるようになります。
PythonSf ワンライナー
tmp:= 3+4
===============================
7
dos command
dir tmp.pvl
ドライブ D のボリューム ラベルは ボリューム です
ボリューム シリアル番号は 4CBC-BC86 です
D:\my\vc7\mtCm のディレクトリ
2012/01/05 06:13 42 tmp.pvl
1 個のファイル 42 バイト
0 個のディレクトリ 41,679,384,576 バイトの空き領域
dos command
type tmp.pvl
# python object printed out by pprint
7
PythonSf ワンライナー
# read tmp.pvl and halve it
=:tmp; tmp/2
===============================
3.5
ファイル変数の もっと実用的な使用例を示します。標準配布している PythonSf のカレント・ディレクトリには X32.pvl,X64.pvl,X28.pvl, Px32.pvl,Px64.pvl,Px128.pvl といった量子力学の行列力学で使うための[-1,1] 範囲の位置演算子行列、[0,2pi] 範囲の運動量演算子行列のファイル変数を入れてあります。X32 は下のようなデータの行列です。
PythonSf ワンライナー
P,X=:Px32,X32; X
===============================
[[-0.96875 0. 0. ..., 0. 0. 0. ]
[ 0. -0.90625 0. ..., 0. 0. 0. ]
[ 0. 0. -0.84375 ..., 0. 0. 0. ]
...,
[ 0. 0. 0. ..., 0.84375 0. 0. ]
[ 0. 0. 0. ..., 0. 0.90625 0. ]
[ 0. 0. 0. ..., 0. 0. 0.96875]]
---- ClTensor ----
位置/運動量演算子行列 X,Px を使って、Hamiltonian 行列を記述できます。Hamiltonian 行列が位置・運動量演算子行列の多項式として与えらるのならば、量子力学の教科書の行列力学の章に書いてある行列力学の方程式が実際に計算できます。例えば調和振動子の Hamiltonian は下のように書けます。
PythonSf ワンライナー
P,X=:Px64, X64; H=P^2+X^2; H
===============================
[[ 4.25805908 +8.32667268e-17j 1.99678801 +9.80959047e-02j
0.49679034 +4.89295777e-02j ..., 0.21901645 -3.24880216e-02j
0.49679034 -4.89295777e-02j 1.99678801 -9.80959047e-02j]
[ 1.99678801 -9.80959047e-02j 4.19751221 +5.55111512e-17j
1.99678801 +9.80959047e-02j ..., 0.12179970 -2.42274668e-02j
0.21901645 -3.24880216e-02j 0.49679034 -4.89295777e-02j]
[ 0.49679034 -4.89295777e-02j 1.99678801 -9.80959047e-02j
4.13891846 -5.55111512e-17j ..., 0.07680678 -1.92390964e-02j
0.12179970 -2.42274668e-02j 0.21901645 -3.24880216e-02j]
...,
[ 0.21901645 +3.24880216e-02j 0.12179970 +2.42274668e-02j
0.07680678 +1.92390964e-02j ..., 4.13891846 +2.04697370e-16j
1.99678801 +9.80959047e-02j 0.49679034 +4.89295777e-02j]
[ 0.49679034 +4.89295777e-02j 0.21901645 +3.24880216e-02j
0.12179970 +2.42274668e-02j ..., 1.99678801 -9.80959047e-02j
4.19751221 +6.80011603e-16j 1.99678801 +9.80959047e-02j]
[ 1.99678801 +9.80959047e-02j 0.49679034 +4.89295777e-02j
0.21901645 +3.24880216e-02j ..., 0.49679034 -4.89295777e-02j
1.99678801 -9.80959047e-02j 4.25805908 -8.32667268e-17j]]
---- ClTensor ----
この Hamiltonian 行列は無限次元 Hilbert 空間の近似式にすぎません。でも、高々 64 x 64 行列による近似式でも、量子力学における調和振動子らしい性質を幾つも備えています。まずは Hamiltonian のエネルギー固有値を昇順に並べたものと、その隣り合う要素間の差分値を見てみましょう。
PythonSf ワンライナーたち
# Hamiltonian の固有値の昇順配列
P,X=:Px64, X64; H=P^2+X^2; eigvalsh(H)
===============================
[ 0.03125000+0.j 0.09375000+0.j 0.15625000+0.j 0.21875000+0.j
0.28125000+0.j 0.34374997+0.j 0.40625022+0.j 0.46874830+0.j
0.53125901+0.j 0.59370001+0.j 0.65642917+0.j 0.71797533+0.j
0.78307742+0.j 0.83758165+0.j 0.91619057+0.j 0.94962095+0.j
1.06362868+0.j 1.07763419+0.j 1.23050560+0.j 1.23652959+0.j
1.41810063+0.j 1.42121437+0.j 1.62625614+0.j 1.62810710+0.j
1.85462810+0.j 1.85582224+0.j 2.10294704+0.j 2.10374776+0.j
2.37102704+0.j 2.37156478+0.j 2.65874147+0.j 2.65908661+0.j
2.96600288+0.j 2.96619493+0.j 3.29274974+0.j 3.29281031+0.j
3.63887701+0.j 3.63893806+0.j 4.00435423+0.j 4.00453612+0.j
4.38921091+0.j 4.38952113+0.j 4.79342210+0.j 4.79387721+0.j
5.21696632+0.j 5.21759441+0.j 5.65982304+0.j 5.66066864+0.j
6.12196967+0.j 6.12310288+0.j 6.60337666+0.j 6.60491066+0.j
7.10399790+0.j 7.10612440+0.j 7.62374802+0.j 7.62681621+0.j
8.16243915+0.j 8.16715679+0.j 8.71954535+0.j 8.72762234+0.j
9.28731293+0.j 9.31657988+0.j 9.75250929+0.j 10.19014824+0.j]
---- ClTensor ----
# Hamiltonian 固有値の差分
P,X=:Px64, X64; H=P^2+X^2; vc=eigvalsh(H); vc=vc-shftSq(vc)
Waring: don't use assignment at last sentence.We ignore the assignment.
===============================
[ 3.12500000e-02+0.j 6.25000000e-02+0.j 6.25000000e-02+0.j
6.24999998e-02+0.j 6.25000026e-02+0.j 6.24999695e-02+0.j
6.25002517e-02+0.j 6.24980750e-02+0.j 6.25107081e-02+0.j
6.24410072e-02+0.j 6.27291558e-02+0.j 6.15461604e-02+0.j
6.51020863e-02+0.j 5.45042324e-02+0.j 7.86089186e-02+0.j
3.34303833e-02+0.j 1.14007733e-01+0.j 1.40055090e-02+0.j
1.52871408e-01+0.j 6.02399218e-03+0.j 1.81571035e-01+0.j
3.11374152e-03+0.j 2.05041772e-01+0.j 1.85096230e-03+0.j
2.26521002e-01+0.j 1.19413904e-03+0.j 2.47124794e-01+0.j
8.00725528e-04+0.j 2.67279275e-01+0.j 5.37743185e-04+0.j
2.87176693e-01+0.j 3.45136237e-04+0.j 3.06916275e-01+0.j
1.92040921e-04+0.j 3.26554815e-01+0.j 6.05733205e-05+0.j
3.46066693e-01+0.j 6.10529677e-05+0.j 3.65416172e-01+0.j
1.81887321e-04+0.j 3.84674788e-01+0.j 3.10218641e-04+0.j
4.03900971e-01+0.j 4.55112728e-04+0.j 4.23089107e-01+0.j
6.28094792e-04+0.j 4.42228631e-01+0.j 8.45595766e-04+0.j
4.61301033e-01+0.j 1.13320700e-03+0.j 4.80273786e-01+0.j
1.53399721e-03+0.j 4.99087243e-01+0.j 2.12649374e-03+0.j
5.17623621e-01+0.j 3.06819454e-03+0.j 5.35622935e-01+0.j
4.71764271e-03+0.j 5.52388560e-01+0.j 8.07698830e-03+0.j
5.59690586e-01+0.j 2.92669528e-02+0.j 4.35929408e-01+0.j
4.37638952e-01+0.j]
---- ClTensor ----
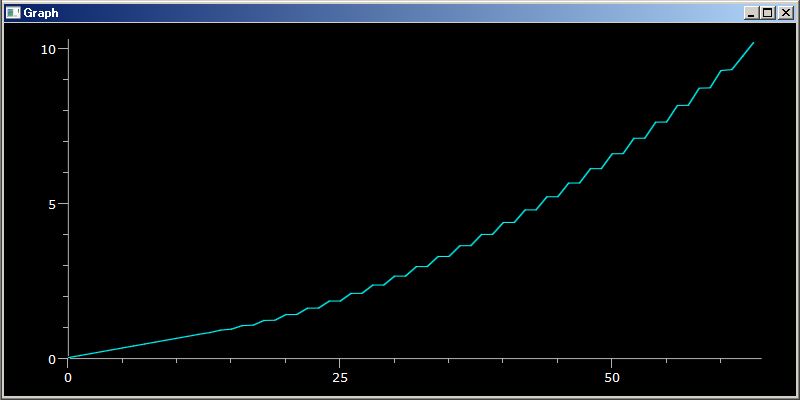
最初の固有値は 2pi h/2:2/64:3.125e-2:0 振動ですが、その次からは 2pi h:4/64:6.25e-2 刻みになっています。0 点振動の近くではエネルギー固有値は 0.0625 刻みで直線上に分布します。でも 0 点振動から離れると直線から二次の曲線に移っていきます。 64 点有限近似の影響が表れてきます。この固有値分布は下のように可視化されます。
PythonSf ワンライナー
P,X=:Px64, X64; H=P^2+X^2; plotGr( eigvalsh(H) )
波動関数の時間変化も、この Hamiltonian 行列から計算できます。
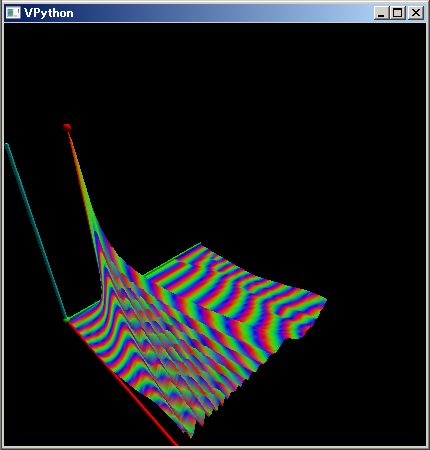
初期状態でインデックス 16 の位置に集中している波動関数ベクトル vc の位相も含めた時間変化:調和振動子波動関数の運動を、下のように自然なワン・ライナーで計算・可視化できます。
PythonSf ワンライナー
P,X=:Px64, X64; H=P^2+10 X^2; vc=kzrs(64); vc[16]=1; renderMtCplx( ~[ expm(`i H t) vc for t in klsp(0, 5s`)])
ファイル変数は何度でも再利用できます。ですからファイル変数を、ある種のカスタマイズ・データとしても利用できます。ファイル変数は行列などの pickable にインスタンスにしか使えないのですが、必要なときにだけ =: で読み出して使うので、他の PythonSf 式の時間負荷になりません。sfCrrntIni.py/customize.py に書かれた Python Code は何時でも PythonSf 式の実行前に import され実行されるので時間負荷となり、応答時間を増大させます。
この意味で、ファイル変数は別の時間負荷とならないカスタマイズ方法としても使えます。
PythonSf では、 基本数値関数 exp, sin, cos, tan, sinh, cosh, tanh, arcsin, arccos, arctan, log, log10, sqrt, absF は、グローバル変数に入れてあり、import 無しで直ぐに使えます。同時に、これらは加減乗除と整数べき乗算および関数合成を可能にしてあります。
PythonSf ワンライナー
x=pi/6; ( 2 sin cos )(x), sin(2`X)(x)
===============================
(0.8660254037844386, 0.8660254037844386)
関数を加減乗除べき乗算と関数合成を可能なものにするために ClAF クラスを設けています。pysf\basicFnctns.py で実装しています。この ClAF で Numpy の exp, sin, cos, tan, sinh, cosh, tanh, arcsin, arccos, arctan, log10, sqrt を包んでやることで、本関数 sin(2pi `X^2) + 1 などの PythonSf 式を可能にしています。
usFn=ClAF(userFunction) と一変数関数:userFunction を包んで usFn などのラベルに割り当ててやれば、usFn が関数合成と加減乗除べき乗算が可能な userFnction の関数機能を持った関数になります。customize.py または sfCrrntIn.py の中に usFn=ClAF(userFunction) コードを書いてやれば usFn が PythonSf 式を実行するときのグローバル変数に入り込みます。このようにカスタマイズしてやることでユーザーが望む関数を import なしで使える、関数合成と加減乗除べき乗算が可能な関数にできます。
exp, sin, cos, tan, sinh, cosh, tanh, arcsin, arccos, arctan, log10, sqrt を ClAF で包むことは pysf\kNumeric.py で行っています。そして customize.py のなかで kNumeri.py を import * してあります。興味のある方は Python ソース・コードを見てみてください。
数学の世界では x,y,z は変数の意味になります。x,y,z が何であるかに言及することなく sin(x^2), cos(2x+1), tan(x+y), exp(x^2+y^2+z^2) などの関数の意味は明確であるとされてしまいます。 「x^2+2x + 3 は二次関数である」というとき、x が何であるかまでは言及しません。
同様なことを可能にするため、 `X,`Y,`Z,`T 変数に加減乗除べき乗算と関数合成が可能な恒等関数を assign するコードを customize.py に書いてあります。`X,`Y,`Z,`T は、一番目の、二番目の、三番目の、最後の引数を取り出す意味も与えてあります。恒等関数といっても加減乗除べき乗算を組み合わせることで任意の多項式関数を表現できます。下のような具合です。
PythonSf ワンライナー
(`X^2+2`X+3)(2) # quadratic function
===============================
11
PythonSf ワンライナー
(`X^2+`Y^2)(2,3) # 2 parameter quadratic function
===============================
13
PythonSf ワンライナー
(`X^2 + `T)(2,3) # `T picks up the last parameter 3
===============================
7
PythonSf ワンライナー
N=6; [(sin(2`X))(n/N) for n in range(N)]
===============================
[0.0, 0.32719469679615221, 0.61836980306973699, 0.8414709848078965, 0.97193790136331271, 0.99540795775176494]
Python には、Numpy, SciPy パッケージという、膨大な数学ライブラリの蓄積があります。SciPy は Numpy を包含します。SciPy のサブパッケージには scipy.optimize,integrate,linalg,special,signal といった Matlab では別の単独パッケージとして売られているような物も入っています。でも Numpy には、これらがありません。
「ならば、nympy ではなく、SciPy だけを使っておけばよい。」とはできません。 SciPy は膨大すぎて、netbook のような非力なパソコンでは import scipy とするだけで、二秒近くかかったりします。一方で Numpy は一桁短い時間で import を終了します。ですから PythonSf では常に import numpy as np を実行しますが、import scipy as sy を実行するのは、sy() を明示的に呼び出したときに限っています。
sy() を呼び出すと import scipy as sy のほかに so,si,sl,ss,sg の名前で下のサブ・パッケージも同時に import しています。これらの サブ・パッケージの import 時間は無視できる程度だからです。これらのサブ・パッケージは下の機能を持っています。
Numpy は pysf.sfFnctns モジュールの中で import numpy as np と import 済みであり、Numpy package にある膨大な機能が np名前空間 の下で全て利用可能です。
PythonSf ワンライナー
# numpy.source(..) 関数は引数に与えられた関数やモジュールのソース・コードを返します
np.source(fft)
In file: pysf\kNumeric.py
def fft(sqAg, n=None, axis = -1):
"""' reverse Fasst Fourier Transform
return ClTensor array
'"""
import numpy.fft as fp
return sf.krry(fp.fft(sqAg, n, axis))
===============================
None
PythonSf ワンライナー
# numpy.info(..) 関数は引数に与えられた関数やモジュールについてのコンパクトな説明を返します。
# help(..) でのように詳細すぎる説明ではありません。
np.info(np.linalg)
Core Linear Algebra Tools
-------------------------
Linear algebra basics:
- norm Vector or matrix norm
- inv Inverse of a square matrix
- solve Solve a linear system of equations
- det Determinant of a square matrix
- lstsq Solve linear least-squares problem
- pinv Pseudo-inverse (Moore-Penrose) calculated using a singular
value decomposition
- matrix_power Integer power of a square matrix
Eigenvalues and decompositions:
- eig Eigenvalues and vectors of a square matrix
- eigh Eigenvalues and eigenvectors of a Hermitian matrix
- eigvals Eigenvalues of a square matrix
- eigvalsh Eigenvalues of a Hermitian matrix
- qr QR decomposition of a matrix
- svd Singular value decomposition of a matrix
- cholesky Cholesky decomposition of a matrix
Tensor operations:
- tensorsolve Solve a linear tensor equation
- tensorinv Calculate an inverse of a tensor
Exceptions:
- LinAlgError Indicates a failed linear algebra operation
===============================
None
PythonSf ワンライナー
# 擬似逆行列の計算
np.linalg.pinv([[1,2,3],[4,5,6]])
===============================
[[-0.94444444 0.44444444]
[-0.11111111 0.11111111]
[ 0.72222222 -0.22222222]]
PythonSf ワンライナー
# 擬似逆行列との積が単位行列になること:上の計算結果の確認
np.dot([[1,2,3],[4,5,6]], np.linalg.pinv([[1,2,3],[4,5,6]]))
===============================
[[ 1.00000000e+00 -4.44089210e-16]
[ 0.00000000e+00 1.00000000e+00]]
なお、Numpy の中でも使用頻度の高いフーリエ変換:fft,ifft,fftshift, 行列の固有値、固有ベクトル:eig,eigvals, 行列の exponential/logarithm/square_root:expm,logm,sqrtm は、グローバル名前空間に再実装してあり、下のように直接呼び出せます。これらの関数の戻り値は ClTensor インスタンスに修正してあります。
PythonSf ワンライナーたち
fft([1,2,3,4])
===============================
[ 10.+0.j -2.+2.j -2.+0.j -2.-2.j]
---- ClTensor ----
eig([[1,2],[3,4]])
===============================
(ClTensor([-0.37228132, 5.37228132]),
ClTensor([[-0.82456484, -0.41597356],
[ 0.56576746, -0.90937671]]))
eigvals([[1,2],[3,4]])
===============================
[-0.37228132 5.37228132]
---- ClTensor ----
expm([[1,2],[3,4]])
===============================
[[ 51.9689562 74.73656457]
[ 112.10484685 164.07380305]]
---- ClTensor ----
sqrtm([[1,2],[3,4]])
===============================
[[ 0.55368857+0.46439416j 0.80696073-0.21242648j]
[ 1.21044109-0.31863972j 1.76412966+0.14575444j]]
---- ClTensor ----
seed(0); rand(2,3)
===============================
[[ 0.5488135 0.71518937 0.60276338]
[ 0.54488318 0.4236548 0.64589411]]
---- ClTensor ----
seed(0); randn(2,3)
===============================
[[ 1.76405235 0.40015721 0.97873798]
[ 2.2408932 1.86755799 -0.97727788]]
---- ClTensor ----
seed(0); randint(10,size=[2,3])
===============================
[[5 0 3]
[3 7 9]]
---- ClTensor ----
seed(0); shuffle(range(10))
===============================
[2, 8, 4, 9, 1, 6, 7, 3, 0, 5]
SciPy パッケージは sy() を呼び出して下のように使います。
PythonSf ワンライナー
sy(); sy.factorial(10), sy.factorial(10, True)
===============================
(array(3628800.0), 3628800L)
SciPy は sy() と関数呼び出しを行ったときに sy のパッケージ名で import されます。このとき同時に import scipy.optimize as so, import scipy.integrate as si, import scipy.linalg as sl, import scipy.special as ss, import scipy.signal as sg も行われます。sy() を一度呼び出すだけで、so,si,sl,ss,sg の下で optimize,integrate,linalg,special,signal のサブ・パッケージ内にある膨大な機能を利用可能になります。
PythonSf ワンライナー
sy(); so.bisect(`X^3+2`X^2-3`X-1, -10,10) # find 0 point by bi-section method
===============================
1.19869124352
PythonSf ワンライナー
# 二重積分:関数 f(x,y)=x^2 + y^2 を、原点から半径 1 の円内の領域で積分する
sy(); si.dblquad(`X^2+`Y^2, -1,1, sqrt(1-`X^2),-sqrt(1-`X^2) )
===============================
(-1.5707963267947727, 1.2484818956437493e-08)
# 右側の 1.2484818956437493e-08 は推定誤差
PythonSf ワンライナー
sy(); sl.sinm(`σx) # sinm(x) == x - x^3/3! + x^5/5! - ...
===============================
[[ 0. 0.84147098]
[ 0.84147098 0. ]]
# 注意 SciPy のユニーバーサル関数は ClTensor 引数値を与えれは ClTensor インスタンスを返す
# でも SciPy 関数の中には、sinm(..) のように ufunc でなくて ClTenso 引数値:`σx を与えても np.ndarray 値を返すものがある。
PythonSf ワンライナー
sy(); ss.zeta(3,0) # special function ζ(..)
===============================
1.79769313486e+308
Numpy の info(..) 関数は非常に便利です。help(..) 関数より、凝縮して情報を表示してくれ、また np.info(..) 関数の情報だけで十分なことが多いからです。パッケージ・モジュール・クラス・関数やインスタンスなどドキュメント文字列を備えた全ての Python オブジェクトに対して使えます。 PythonSf 式だけに限らずに、np.info(..) 関数は Python 一般で、もっと使われるべきです。
PythonSf ワンライナー
np.info(set)
set()
set() -> new empty set object
set(iterable) -> new set object
Build an unordered collection of unique elements.
Methods:
difference_update -- Remove all elements of another set from this set.
symmetric_difference -- Return the symmetric difference of two sets as a new set.
pop --
issuperset -- Report whether this set contains another set.
remove -- Remove an element from a set; it must be a member.
issubset -- Report whether another set contains this set.
union -- Return the union of sets as a new set.
add -- Add an element to a set.
discard -- Remove an element from a set if it is a member.
intersection -- Return the intersection of two or more sets as a new set.
symmetric_difference_update -- Update a set with the symmetric difference of itself and another.
update -- Update a set with the union of itself and others.
difference -- Return the difference of two or more sets as a new set.
copy -- Return a shallow copy of a set.
isdisjoint -- Return True if two sets have a null intersection.
clear -- Remove all elements from this set.
intersection_update -- Update a set with the intersection of itself and another.
===============================
None
np.source(..) 関数は、モジュール、クラス、関数の Python source code を表示する関数です。Python は短く書けるけれど可読性に優れた言語です。下手なドキュメントよりソース・コードを読んだ方が良く解ることが珍しくありません。Python document 文字列だけでは解りにくいときは、そのソース・コードを見てみましょう。下のような具合です。
PythonSf ワンライナー
np.source(mitr)
In file: pysf\basicFnctns.py
def mitr(*args):
""" 多次元の繰り返しを生成するジェネレータ
generator generating for multiple dimention iterators
e.g.
list(mitr(2,3))
===============================
[(0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2)]
s=set(['a','b']);list(mitr(s,s))
===============================
[('a', 'a'), ('a', 'b'), ('b', 'a'), ('b', 'b')]
s=[1,2,3];list(mitr(s,s))
===============================
[(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)]
"""
head, tail = args[0], args[1:]
if type(head) in [int, long, float]:
head = range(int(head))
if tail:
if len(tail) == 1 and hasattr(tail[0],'next'):
# to avoid multiple use of one iterator
tailAt = (tuple(tail[0]), )
else:
tailAt = tail
for i in head:
for j in mitr(*tailAt):
if len(tail) == 1:
yield (i, j)
else:
yield (i,)+j
else:
for i in head:
yield i
===============================
None
ついでですが、上の mitr(..) generator は多重ループを一つのイタレータで済ますようにする generator 関数です。PythonSf ワンライナーでは短く多重ループ処理を記述できるので多用します。上のソースを追ってみれば、mitr(..) generator が関数プログラミング的に実装されており、任意の N 重ループも扱えることまで解るでしょう。
ちなみに上の mitr(..) の機能は itertools.product の機能と同じです。itertools.product(..) が実装される前から mitr(..) を使っているため、また次の enumitr(..) 関数との整合性を保つため mitr(..) を使い続けます。
enmitr(..) は mitr(..) の機能に加えて、整数インデックスも返すので、行列・テンソル・データの作成に便利です。次のような具合です。
PythonSf ワンライナー
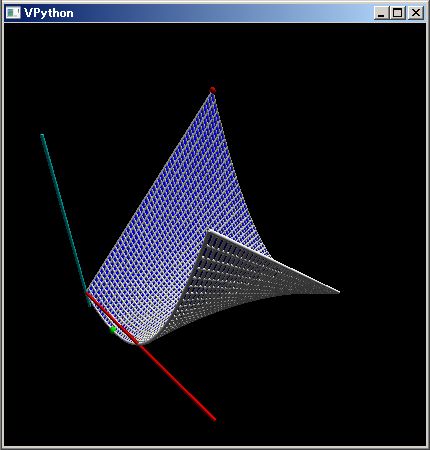
# [-1,1]x[-1,1] の領域での x^2 - x y 関数分布を行列データとして作り、表示させる
dct={}; v=klsp(-1,1); for idx,pos in enmitr(v,v):dct[idx]=(`X^2-`X `Y)(*pos); renderMtrx(dct)
分からないコードが出てきたときは、np.info(..), np.source(..) を使った PythonSf ワンライナーで、その機能や使い方を調べられます。上の klsp(..) の意味が分からないときは、これらを使って調べましょう。PythonSf のワンライナーを使えば、その確認・実行は簡単です。
PythonSf ワンライナーたち
# klsp のソース: Numpy の linspace に kryy(..) 関数を被せて ClTesnor インスタンスを変えているだけ
np.source(klsp)
In file: pysf\basicFnctns.py
def klsp(*sq, **dct):
"""' return ClTensor of scipy.linspace(...)
'"""
return sf.krry(sc.linspace(*sq, **dct) )
===============================
None
# [-1,1] の範囲を 49 等分する 50 点の ClTesor データ
klsp(-1,1)
===============================
[-1. -0.95918367 -0.91836735 -0.87755102 -0.83673469 -0.79591837
-0.75510204 -0.71428571 -0.67346939 -0.63265306 -0.59183673 -0.55102041
-0.51020408 -0.46938776 -0.42857143 -0.3877551 -0.34693878 -0.30612245
-0.26530612 -0.2244898 -0.18367347 -0.14285714 -0.10204082 -0.06122449
-0.02040816 0.02040816 0.06122449 0.10204082 0.14285714 0.18367347
0.2244898 0.26530612 0.30612245 0.34693878 0.3877551 0.42857143
0.46938776 0.51020408 0.55102041 0.59183673 0.63265306 0.67346939
0.71428571 0.75510204 0.79591837 0.83673469 0.87755102 0.91836735
0.95918367 1. ]
---- ClTensor ----
# [-1,1] の範囲を 5 等分する 6 点の ClTesor データ
klsp(-1,1, 6)
===============================
[-1. -0.6 -0.2 0.2 0.6 1. ]
---- ClTensor ----
np.inf(..), np.source(..) や PythonSf ワンライナーを使ってドキュメント文字列を調べたり、テスト・コードを実行してみることは PythonSf 式の作成だけに限らず、Python プログラミング一般の作成でも有効です。活用ください。
np.array(..) を使って生成する np.ndarray インスタンスは使いにくいので、PythonSf では ClTensor または ClFldTns インスタンスを主に使います。整数、実数・複素数を要素とする行列・ベクトルには ClTensor を使います。それ以外の一般の環・体を要素とする行列・ベクトルには ClFldTns を使います。~[...] 記法で作られるインスタンスのタイプは ClTensor または ClFldTns のどちらかです。
np.ndarray インスタンスが使いにくいのは下の理由によります。
実際に numpy.ndarray 使ってみると、浮動小数点タイプの行列やベクトルを作ったつもりなのに整数タイプの行列ができてしまうことが非常に困ります。それらしく動いてしまうので、分からないまま少しだけ値が違う計算が入り込んでミスに気づかずに計算作業を蓄積していってしまうからです。後でミスを見つけ出すのが厄介だからです。数学の世界では浮動小数点と整数を区別しないことが大部分であり、注意していても その癖がどうしても入り込んでしまいます。ClTensor クラスは np.ndarray を継承しているのですが、デフォルトで浮動小数点タイプの行列やベクトルを生成するようにしてあります。
敢えて ClTensor を導入するのですから、np.dot(..) 関数を使わなくてもすむように、__mul__(..), __pow__(...) などの加減乗除べき乗算に対応する関数を定義した実装にしました。これにより、日常のメモ書きに近い PythonSf 数式による行列やベクトルの演算が可能にできました。
ClTensor インスタンスと tuple, list といった Python シーケンスも、そのサイズさえ合えば、ClTensor インスタンスとの加減乗除算をできるようにしています。ですから Matlab などと違って、縦ベクトル・横ベクトルの概念を使うことなく、行列とベクトルとの積や内積演算が行えるようにしてあります。下のような具合です。
PythonSf ワンライナーたち
# 内積
vc=~[1,2,3]; vc ~[4,5,6]
===============================
32.0
# ベクトルとリストの内積
vc=~[1,2,3]; vc [4,5,6]
===============================
32.0
~[k for k in range(1,4)] [4,5,6]
===============================
32.0
vc=~[1,2,3]; vc range(4,7)
===============================
32.0
# ベクトルとタプルの内積
vc=~[1,2,3]; vc (4,5,6)
# 行列とベクトルの積
mt = ~[[1,2],[3,4]]; mt ~[5,6]
===============================
[ 17. 39.]
---- ClTensor ----
# 行列 * リスト
mt = ~[[1,2],[3,4]]; mt [5,6]
===============================
[ 17. 39.]
---- ClTensor ----
# リスト * 行列
mt = ~[[1,2],[3,4]]; [5,6] mt
===============================
[ 23. 34.]
---- ClTensor ----
# 行列とタプルの積
mt = ~[[1,2],[3,4]]; mt (5,6)
===============================
[ 17. 39.]
---- ClTensor ----
SciPy より小さいとはいえ、Numpy package には PythonSf で頻繁に使うランダム関数、高速フーリエ変換、線形代数パッケージが備わっています。PythonSf では numpy の import 時間が短いことより、これらを積極的に利用しています。
これらは np.random.rand(...) などと呼び出せるのですが、使う頻度からすると np.random などのモジュール名を何度も打ち込むのは面倒すぎます。Global な名前空間に、これらの関数名を置いておくべきです。同時に、これらが返すインスタンスのタイプが np.ndarray であることが、行列やベクトルの積演算を面倒にしてくれるので対策が望まれます。ですから、これらの対策を施した以下のバッファ関数を PythonSf のグローバル名前空間に実装・追加しています。
numpy.random モジュールは整数乱数生成関数:randint(..)、0-1一様分布ランダム関数:rand(..)、正規分布ランダム関数:randn(..),シーケンス・データのランダムな入れ替え関数:shuffle(..) といった便利に使える関数が備わっています。これらは行列やベクトルの乱数も生成でき非常に便利です。
rand(..) 関数には、下のようにバッファ関数を設けてあります。
np.source(rand)
In file: pysf\kNumeric.py
def rand(*sqAg):
if len(sqAg) == 0:
return (sf.sc.random.rand(*sqAg))
else:
return sf.krry(sf.sc.random.rand(*sqAg))
===============================
None
seed(..), randint(..), randn(..) と shuffle(..) も同様に置き換えてあるので、次のような PythonSf 式を使った計算が可能になります。
PythonSf ワンライナーたち
# [0,1] の範囲でのランダム変数を返す
seed(0); rand()
===============================
0.548813503927
# [0,1] の範囲でのランダム変数行列を返す
seed(0); rand(2,4)
===============================
[[ 0.5488135 0.71518937 0.60276338 0.54488318]
[ 0.4236548 0.64589411 0.43758721 0.891773 ]]
---- ClTensor ----
# 正規分布でのランダム変数行列を返す
seed(0); randn(2,4)
===============================
[[ 1.76405235 0.40015721 0.97873798 2.2408932 ]
[ 1.86755799 -0.97727788 0.95008842 -0.15135721]]
---- ClTensor ----
# 0 から 1 の整数値を要素とするランダムな行列
randint(9,size=[2,5])
===============================
[[5 6 7 3 1]
[8 1 1 7 4]]
---- ClTensor ----
# デフォルトの浮動小数点タイプ要素からなるランダム行列
~[randint(9,size=[2,5])]
===============================
[[ 1. 0. 5. 2. 4.]
[ 5. 1. 8. 5. 6.]]
---- ClTensor ----
# BOOL 体:1 or 0 を要素とするランダム行列
~[randint(2,size=[2,5]), oc.BF]
===============================
[[0 1 0 0 1]
[1 1 0 0 0]]
---- ClFldTns:< class 'pysf.octn.BF'> ----
下の PythonSf 式は sin(2θ)==2sin(θ)cos(θ) の公式を数値実験で確認しています。
PythonSf ワンライナー
# sin(2θ)== 2sin(θ)cos(θ) の証明・確認
vc=randn(10); [sin(2θ) for θ in vc] ~== [2 sin(θ) cos(θ) for θ in vc]
===============================
True
# 複素数値でも sin(2θ)== 2sin(θ)cos(θ)
mt=randn(2,10);vc=mt[0,:]+`i mt[1,:]; [sin(2θ) for θ in vc] ~== [2 sin(θ) cos(θ) for θ in vc]
===============================
True
上の PythonSf ワン・ライナー式を実行することで「正規表現分布するランダムなθに対し sin(2θ) が 2sin(θ)cos(θ) と六桁以上一致することを 10 回確認した」ことになります。~== はユーザー定義の中置演算子であり、nearlyEq(..) 関数を customize.py でアサインしてあります。これは六桁の精度で一致すれば True を返します。(浮動小数点演算ではコンピュータの計算誤差により、数学公式が成り立たないことが普通なので == 演算子は使えません。)負数も含めて、六桁の精度で十回一致することは sin(2θ)==2sin(θ)cos(θ) が成り立つことを証明したといっても過言ではないでしょう。人間の論証による証明では、それよりずっと多くの確率で誤りが入り込むからです。
このような確認・証明のために random 関連の関数が便利に使えます。
numpy.random モジュールには shuffle(..) 関数があり、シーケンス引数の中身を置換してくれます。ただし np.random.shuffle(..) 関数の戻り値は None です。引数シーケンス・レファランスが指しているシーケンス・データの中身を書き換えます。でもワンライナーで書くときには、戻り値も引数レファレンスを返すことが強く望まれます。shuflle(..) 関数もグローバル変数名にすることも含めて、PythonSf グローバル変数の shuflle(..) 関数は下のように修正してあります。
PythonSf ワンライナー
np.source(shuffle)
In file: pysf\kNumeric.py
def shuffle(sqAg):
sf.sc.random.shuffle(sqAg)
return sqAg
===============================
None
この結果、下のような使い方ができます。
PythonSf ワンライナー
shuffle(range(10))
===============================
[1, 7, 4, 9, 0, 2, 5, 3, 6, 8]
# 比較: NumPy の shuffle(..) 関数
np.random.shuffle(range(10))
===============================
None
高速フーリエ(逆)変換は多くの分野で頻繁に使われます。PythonSf のグローバル名前空間に置くべきです。同時に ClTensor インスタンスを返すようにしたほうが便利です。このように考えて numpy.fft package の fft,ifft 関数のバッファ関数 fft,ifft および fftshift をグローバル変数領域に置いてあります。戻り値も ClTensor インスタンスを返すように修正してあります。
ただし Numpy の fft(..) ifft(..) はベクトルの norm を保存しません。Matlab と同様にスペクトル密度を保つようにフーリエ(逆)変換されます。でも数学的には ノルムを保つフーリエ(逆)変換が望まれることも多くあります。このため nft(..), inft(..):ノルムを保つフーリエ(逆)変換もグローバル変数空間に追加してあります。
なお FFT といっても、任意のベクトル長を対象にフーリエ変換します。2^N 長に限りません。以下のような具合です。
PythonSf ワンライナーたち
N=7; fft(range(N))
===============================
[ 21.0+0.j -3.5+7.26782489j -3.5+2.79115686j -3.5+0.79885216j
-3.5-0.79885216j -3.5-2.79115686j -3.5-7.26782489j]
---- ClTensor ----
N=7; ifft(fft(range(N)))
===============================
[ 2.91830052e-15+0.j 1.00000000e+00+0.j 2.00000000e+00+0.j
3.00000000e+00+0.j 4.00000000e+00+0.j 5.00000000e+00+0.j
6.00000000e+00+0.j]
---- ClTensor ----
N=7; nft(range(N))
===============================
[ 7.93725393+0.j -1.32287566+2.7469796j -1.32287566+1.05495813j
-1.32287566+0.30193774j -1.32287566-0.30193774j -1.32287566-1.05495813j
-1.32287566-2.7469796j ]
---- ClTensor ----
N=7; inft(nft(range(N)))
===============================
[ 2.85344905e-15+0.j 1.00000000e+00+0.j 2.00000000e+00+0.j
3.00000000e+00+0.j 4.00000000e+00+0.j 5.00000000e+00+0.j
6.00000000e+00+0.j]
---- ClTensor ----
N=7; norm(fft(range(N))) ~== ( sqrt(N) norm(nft(range(N))))
===============================
True
行列の指数関数:expm(.), 対数関数:logm(.), 平方根関数 sqrtm(.) や固有値を求める関数eigvals(.)/eigvalsh(.)、行列の固有値と固有ベクトルを求める関数:eig(.)/eigh(.) もグローバル変数空間におくと同時に ClTensor インスタンスを返すように修正してあります。下のような具合です。
PythonSf ワンライナーたち
t=0.1; expm(`σx t)
===============================
[[ 1.00500417 0.10016675]
[ 0.10016675 1.00500417]]
---- ClTensor ----
t=0.1; logm( expm(`σx t) )
===============================
[[ -9.02056208e-17 1.00000000e-01]
[ 1.00000000e-01 -9.02056208e-17]]
---- ClTensor ----
t=0.1; sqrtm(`σx t)
===============================
[[ 0.15811388+0.15811388j 0.15811388-0.15811388j]
[ 0.15811388-0.15811388j 0.15811388+0.15811388j]]
---- ClTensor ----
t=0.1; sqrtm(`σx t)^2
===============================
[[ 0.0+0.j 0.1+0.j]
[ 0.1+0.j 0.0+0.j]]
---- ClTensor ----
t=0.1; eigvalsh(`σx t)
===============================
[-0.1 0.1]
---- ClTensor ----
t=0.1; eigh(`σx t)
===============================
(ClTensor([-0.1, 0.1]),
ClTensor([[-0.70710678, 0.70710678],
[ 0.70710678, 0.70710678]]))
t=0.1; mt=`σx t; mt[1,1]=3; eigvals(mt)
===============================
[-0.00332964 3.00332964]
---- ClTensor ----
t=0.1; mt=`σx t; mt[1,1]=3; eig(mt)
===============================
(ClTensor([-0.00332964, 3.00332964]),
ClTensor([[-0.99944614, -0.03327794],
[ 0.03327794, -0.99944614]]))
その他の SciPy 非ufunc で頻繁に使うものがあるときは、これらと同様なバッファ関数を作り、ClTensor インスタンスを返すようにして customize.py などに実装しておくと便利です。
なお、ベクトルや行列専用のプリント関数 pp(.) を設けてあります。不必要な 0 出力を抑圧することで、計算結果を人間にとって見やすくします。下のような具合です。
PythonSf ワンライナー
t=0.1; pp(sqrtm(`σx t)^2)
[[ 0, 0.1]
,[ 0.1, 0]]
-------- pp --
===============================
None
SymPy パッケージにより symbolic な数式処理を可能にします。SymPy はまだ出来立てであり、Mathematica, Maxima などと比較すれば見劣りします。何百行にもなるプログラムで SymPy を使いまくれば、たぶん SymPy のバグに遭遇するでしょう。でもワンライナーで記述できるようなレベルでは十分に実用的なレベルにあります。
PythonSf で SymPy を利用するには ts() 関数を最初に呼び出します。この関数呼び出しにより「import sympy as ts」が実行されるとともに、`x,`y,`z,`t の SymPy シンボリック変数が定義されます。これにより以下のようなシンボリックな演算処理が可能になります。
PythonSf ワンライナーたち
# x+y+z = 6
# x-y = 0 を x,y 変数に対して解く
ts(); ts.solve( [`x+`y+`z-6, `x-`y], [`x,`y] )
===============================
{x: -z/2 + 3, y: -z/2 + 3}
# (x+z) y = 6
# x-y = 0 を x,y 変数に対して解く
ts(); ts.solve( [(`x+`z) `y-6, `x-`y], [`x,`y] )
===============================
[(-z/2 + (z**2 + 24)**(1/2)/2, -z/2 + (z**2 + 24)**(1/2)/2),
(-z/2 - (z**2 + 24)**(1/2)/2, -z/2 - (z**2 + 24)**(1/2)/2)]
PythonSf では SI 単位系付の数値計算が可能です。sympy.physics.unit の単位を利用しています。「`」による名前空間の拡張を利用して customize.py の中で A`,Ω`,V` などに電流、抵抗、電圧などの単位を割り振っています。っています。SymPy を利用するので ts() を呼び出してから使えるようになります。下のような具合です。
PythonSf ワンライナーたち
# 電圧/電流--> 抵抗
ts(); V,I=3.0V`, 2 A`; V/I
===============================
1.5*V`/A`
# 電圧/抵抗 --> 電流
ts(); V,R=3.0V`, 1.5Ω`; V/R
===============================
2.0*A`
f` p` n` u` mili` k` M` G` hour` min` s` ms` us` ns` ps` kg` g` =1, nm` um` mm` cm` m` met met km` inch` feet` mile` C` A` mA` uA` V` mV` uH` F` uF` pF` Ω` kΩ` ohm` Hz` N` J` mLght` の単位を customize.py で定義してあります。この部分の Python code を追加修正することで、ユーザーの望みの単位を追加できます。
下の主だった物理定数も単位付きで customize.py に定義してあります。
Python コード
#=========== 物理定数 begin ==================================
# light velosity m/s
k_c_bq____ = 2.99792458e+8 * ut.m / ut.s #@:c` --> k__bq__c___
# プランク定数 h/2π 1.054571628(53)×10-34 J s
k_h_bq__bq____ = 1.054571628e-34 * ut.J * ut.s #@:h`` --> h/(2π)
k_h_bq____ = 6.62606896e-034 * ut.J * ut.s #@:h` -->
#ボルツマン定数 J K^-1。 K は絶対温度の単位です。 Joule/Kelvin
k_kB_bq____ = 1.380662e-23 * ut.J / ut.K #@:kB` -->
#万有引力定数 gU` = 6.67259 ×10-11 N` m`^2 `kg-2
k_gU_bq____ = 6.67259e-11 * ut.N * ut.m**2 / ut.kg**2 #@:gU` -->
#重力加速度 gH` = 9.80665 m s-2
k_gH_bq____ = 9.80665 * ut.m / ut.s**2 #@:gH` -->
#素電荷 eQ` = 1.6021892 ×10-19 C
k_eQ_bq____ = 1.6021892e-19 * ut.C
#電子質量 eM` = 9.10938188 ×10^-31 kg
k_eM_bq____ = 9.10938188e-31 * ut.kg
#陽子質量 pM` = 1.67262157 ×10^-27 kg
k_pM_bq____ = 1.67262157e-27 * ut.kg
#水素原子質量 HM` = 1.6735 ×10^-27 kg
k_HM_bq____ = 1.6735e-27 * ut.kg
#モル数,Avogadro 数 NA` = 6.02214199 ×10^23 mol-1
k_NA_bq____ = 6.02214199e+23 / ut.mol
#モル体積 Vm` = 2.241383 ×10-2 m3mol-1
k_Vm_bq____ = 2.241383e-2 * ut.m**3 / ut.mol
#真空の透磁率 1.2566370614E-06 == 4`π 1e-7, 物理単位 N` A`^-2 == henry/meter == weber/(ampere meter)
k__sMu_0_bq____ = 1.2566370614e-6 * ut.H/ut.m #@μ0` -->
k_u0_bq____ = 1.2566370614e-6 *ut.H/ut.m
# 真空の誘電率 ε0 == 1/(`c^2 4`π 1e-7)==クーロン**2 / (newton * M ** 2) == farad/meter == coulomb/(volt meter)
k__sEpsilon_0_bq____ = 8.854187816e-12 * ut.F/ut.m #@:ε0` -->
k_e0_bq____ = 8.854187816e-12 * ut.F/ut.m
#ボルツマン定数 J K^-1 K は絶対温度の単位です。Kg ではありません
k_kB_bq____ = 1.380662e-23 * ut.J/ut.K # Joule/ kelvin degree
#=========== 物理定数 end = ==================================
ですから、下のようなワンライナー計算ができます。
PythonSf ワンライナー
# E == m c^2 == h ν
# ∴ ν== m c^2/h
# 電子の四次元時空での振動数
ts(); eM` c`^2/h`
===============================
1.23558993864461e+20/s`
どんな単位、どんな物理定数が必要なのかはユーザーの専門分野によって大きく変わってきます。PythonSf での物理単位・物理定数は customize.py にある Python code で定まります。この Python code を変更することで、ユーザーの望むとおりに単位系・物理定数変数名をカスタマイズできます。
数値だけからなる単位や物理定数も便利であり、また必要になることがあります。
単位系付きの PythonSf 式の利点の一つとしてドキュメント性の向上があります。「15V` * 1.3A`」と書けば電圧値と電流値を掛け合わせているのであり、電力値:ワットを求めようとしていることを、PythonSf 式だけから読み取れます。
一方で SymPy 単位付きの値を引数として扱えるのは SymPy の関数と PythonSf の基本関数・その加減乗除べき乗合成関数に限られます。NumPy など一般の Python 関数は SymPy 単位付きの値を引数として扱えません。たとえ単位どうしが打ち消しあって無次元の物理量になったとしても、普通の関数では扱えません。下のようなエラーになります。
PythonSf ワンライナーたち
# Numpy の sin 関数に SymPy 単位付きの引数値を与える
ts(); np.sin( 2pi 50Hz` 0.1s`)
Traceback (most recent call last):
sniped
AttributeError: sin
# sin(..):PythonSf 基本関数に SymPy 単位付きの引数値を与える
ts(); sin( 2pi 50Hz` 0.1s`)
===============================
2.32806687965e-15
sin(..) 関数の引数に単位付きの引数が入ってくることは、自然法則を記述する物理ではありえないことです。ですから PythonSf では sqrt,absF 以外の PythonSf 基本関数に、単位が打ち消しあっていない単位付きの引数を与えるとエラーにしています。
PythonSf ワンライナーたち
# sin PythonSf 基本関数に SymPy 単位付きの引数値を与える
ts(); sin( 2pi 50Hz` )
Traceback (most recent call last):
File "C:\Python27\lib\runpy.py", line 162, in _run_module_as_main
"__main__", fname, loader, pkg_name)
File "C:\Python27\lib\runpy.py", line 72, in _run_code
exec code in run_globals
File "D:\my\vc7\mtCm\sfPP.py", line 2, in
pysf.sfPPrcssr.start()
File "pysf\sfPPrcssr.py", line 2776, in start
__execLine( (" ".join(sys.argv[1:])).strip() )
File "pysf\sfPPrcssr.py", line 2392, in __execLine
valStt = eval(ustConvertedAt, globals(), locals() )
File "", line 1, in
File "pysf\basicFnctns.py", line 854, in __call__
return self.m_fn(lstGlbAt['Float'](agAt))
File "pysf\customize.py", line 750, in Float
+ str(fnAt)
AssertionError: At Float(.), you set physical quantity parameter,the units of which are not cancelled:314.159265358979/s`
ts(); sqrt( 2pi 50Hz` )
===============================
17.7245385090552/s`**(1/2)
ts(); absF(-2pi 50Hz` )
===============================
314.159265358979/s`
でも自然法則を使って制御する工学では単位付き引数を使った関数が頻出します。例えば周波数に応じて出力電圧が変わるフィルタ回路の特性を exp(..) などの式で表すなどです。
一方でドキュメント性のためだけならば Hz` などの単位に SymPy 単位付きの値を割り振る必要はありません。Hz` や s` に数値 1 だけを割り振っておいても、ドキュメント性は損なわれません。ならば ts() を呼び出さないときは、単位系には数値の 1 を入れておくだけにしとくべきだ。SymPy 単位系を付けずにおくべきだ。ならば下のようなドキュメント性のある PythonSf 計算式が一般の Python 関数でも可能になる。そうすれば下のような計算が可能になる。
PythonSf ワンライナー
np.sin( 2pi 50Hz` 0.1s`)
===============================
2.32806687965e-15
このように考えて ts() を実装してあります。興味のある方は pysf.customize.ts(..) 関数のソースを読んでみてください。
SI 単位系の規格書は理由なしに、如何に使うかのみを説明しています。さらに SI 単位系は歴史的な経緯に妥協して制定されています。大部分の技術者にとって、電流のほかに電圧:V:Volt または抵抗:Ω:ohm も基本単位なのに、SI 単位系では電流:A のみを基本単位としています。結果として、抵抗値や電圧値は MKSA の四つの基本単位の組み合わせとなります。実際 sympy.physics.units の単位系の実装は、SI 単位系規格書どおりの実装となっています。下のような単位付きの計算結果となります。
PythonSf ワンライナー
# 抵抗値 * 電流値:R I == 電圧値:V
import sympy.physics.units as ut; R,I=1.5ut.ohm, 2ut.A; R I
===============================
3.0*m**2*kg/(A*s**3)
# 電圧値 / 電流値:V/I == 抵抗値:ohm
import sympy.physics.units as ut; V,I=3.0ut.V , 2ut.A; V/I
===============================
1.5*m**2*kg/(A**2*s**3)
でも電圧の単位が「m**2*kg/(A*s**3)」と、また抵抗の単位が「m**2*kg/(A**2*s**3) 」と表記されて分る技術者が、どれだけいるでしょうか。技術者の大部分は A,V の二つを基本単位として電気・電子工学を理解しています。ですから MKSA ではなく MKSAV 単位系として実用的な単位系を構築すべきです。そのように PythonSf の単位系は実装してあります。上の計算は、PythonSf では下のようになります。
PythonSf ワンライナーたち
# 抵抗値 * 電流値:R I == 電圧値:V
ts(); R,I=1.5Ω`, 2A`; R I
===============================
3.0*V`
# 電圧値 / 電流値:V/I == 抵抗値:ohm: V/A
ts(); V,I=3.0V` , 2A`; V/I
===============================
1.5*V`/A`
この MSKAV 単位系という主張は理解してもらいにくいのですが、如何でしょうか。理解してもらえるかとは関係なしに、上のような単位系計算でなければ使い物にならないと考えています。
ただし MKSAV 単位系は冗長であり W` s`/J`の整数べき乗を掛けることによる変換はユーザーが自分で行わねばなりません。A` V` s==W` s`==J`== kg` m`^2 s`^-2 を使って、ユーザーが機械系・電磁系または電流系・電圧系どちらかの単位系を選択するかを下の様に明示的に行わねばなりません。少し面倒ですが、これが大部分のエンジニアが理解している単位系だと思います。
下に PythonSf MKSAV 単位系での計算結果を幾つか示します。
PythonSf ワンライナーたち
# 電圧値 * 電流値:V I == 電力:W`: A V
ts(); V,I=3.0V` , 2A`; V I
===============================
6.0*A`*V`
# 電圧値 * 電流値:V I == 単位時間当たりの仕事:J`/s`
ts(); V,I=3.0V` , 2A`; V I J`/(W` s`)
===============================
6.0*m`**2*kg`/s`**3
# 1m 離した 1A の電線の間にに働く 1m 当りの力 1
ts(); u0` A`^2/(2pi m`)
===============================
1.99999999994284e-7*A`*s`*V`/m`**2
# 1m 離した 1A の電線の間に働く 1m 当りの力 2
ts(); u0` A`^2/(2pi m`) J`/s`/W`
===============================
1.99999999994284e-7*kg`/s`**2
# 1m 離した 1C の電荷どうしの間に働く力 1
ts(); 1.0C`^2/(4pi e0` 1m`^2)
===============================
8987551789.01297*A`*s`*V`/m`
# 1m 離した 1C の電荷どうしの間に働く力 2
ts(); 1.0C`^2/(4pi e0` 1m`^2) J`/s`/W`
===============================
8987551789.01297*kg`*m`/s`**2
# 1C の電荷が 1m 離れた位置に作る電場
ts(); 1.0C`/(4pi e0` 1m`^2)
===============================
8987551789.01297*V`/m`
# 1C の電荷が 1m 離れた位置に作る電位
ts(); 1.0C`/(4pi e0` 1m`)
===============================
8987551789.01297*V`
# 1uH のコイルに 1A の電流を流したときにできる磁束Φ
ts(); 1.0uH` 1A`
===============================
1.0e-6*s`*V`
# 微細構造定数 1
ts(); eQ`^2/(4pi ε0` h`` c`)
===============================
0.00729746834685501*A`*s`**3*V`/(kg`*m`**2)
# 微細構造定数 2
ts(); eQ`^2/(4pi ε0` h`` c`) J`/s`/W`
===============================
0.00729746834685501
上と同様な計算を sympy.physics.units:MKSA 単位系で行うと下のようになります。
PythonSf ワンライナーたち
# 電圧値 * 電流値:V I == 電力
import sympy.physics.units as ut; 3.0 ut.V 2ut.A
===============================
6.0*kg*m**2/s**3
# 1m 離した 1A の電線の間に働く 1m 当りの力
import sympy.physics.units as ut; ut.u0 1.0ut.A^2/(2pi ut.m)
===============================
6.36619772367581e-8*pi*kg/s**2
# 1C の電荷が 1m 離れた位置に作る電場
ts(); import sympy.physics.units as ut; 1.0ut.C/(4pi ut.e0 1ut.m^2) 3.14159265359/ts.pi
===============================
8987551787.36877*kg*m/(A*s**3)
# 1C の電荷が 1m 離れた位置に作る電位
ts(); import sympy.physics.units as ut; 1.0ut.C^2/(4pi ut.e0 1ut.m^2) 3.14159265359/ts.pi
===============================
8987551787.36877*kg*m/s**2
# 1uH のコイルに 1A の電流を流したときにできる磁束Φ
import sympy.physics.units as ut; 1e-6 ut.H ut.A
===============================
1.0e-6*kg*m**2/(A*s**2)
# 微細構造定数
ts(); import sympy.physics.units as ut; eQ,h,c=1.6021892e-19 ut.A ut.s, 1.054571628e-34 ut.kg ut.m^2/ut.s, 299792458.0ut.m/ut.s; eQ^2/(4.0 pi ut.e0 h c) 3.14159265359/ts.pi
===============================
0.00729746834552000
微細構造定数では SI:MKSA 単位系のほうが無条件で無次元の単位を表示してくれて便利です。でも頻繁に出てくる電場や電位の単位が kg*m/(A*s**3) や kg*m/s**2 では使い物になりません。これでは何を意味しているのか分りません。
PythonSf MKSAV 単位系ならば電場や電圧は V`/m`, V` で表示してくれます。たとえ J`/s`/W` などを掛けることが出てくるにしても、これならば実用的に使えます。そして、このような冗長な単位系が実際のエンジニアが使っている単位系です。
Python には pylab, mayavi といったグラフ表示パッケージがあります。これらは 3D 表示まで可能な素晴らしいものです。論文に載せる品質のグラフも描けます。
でも、グラフを描くのに手間がかかりすぎます。自分のために描くグラフならば凡例なんぞ要りません。多くの場合は横軸スケール値さえ要りません。ユーザー自身が分っていることが多いからです。それよりも最小の手間でグラフ情報を表示させるほうが優先されます。ワンライナーでグラフ表示させるときは、一刻でも早くどんな分布をしているのか見たくてしょうがないのですから。そのために PythonSf では plotGr(..), plotTrajectory(..), plot3dGr(..), renderFaces(..), plotTmCh(..) といった関数を用意しています。
PythonSf ワンライナー
plotGr(sin( 2pi `X^2) )
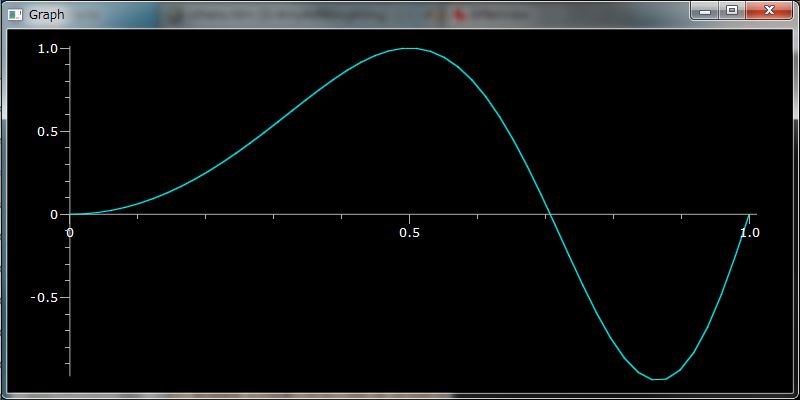
範囲 [-2,3] データ点数 256 で表示させるときは下のように引数パラメータを増やします
PythonSf ワンライナー
plotGr(sin( 2pi `X^2), -2, 3, 256)
tuple, list, array などのシーケンス・データを与えることでもグラフを表示させられます。ただし、このとき横軸は len(シーケンス・データ) になっています。でもユーザーは横軸の範囲が [-2,2] であることは分っているので問題ありません。 plotGr([sin( 2pi `X^2)(t) for t in klsp(-2,2, 128)]) の PythonSf 式を書いたユーザーがグラフを見ているのですから。
PythonSf ワンライナー
plotGr([sin( 2pi `X^2)(t) for t in klsp(-2,2, 128)])
plotTrajectory(..) は引数に二次元位置のデータからなるシーケンス・データを与えることで、それらの位置を直線で結んだ二次元グラフを表示させます。下のような具合です。
PythonSf ワンライナー
plotTrajectory([(0.9 cos(θ),sin(2θ)) for θ in arsq(0, 256,2pi/256)])
三次元位置のシーケンスを与えると、三次元の軌跡を描きます。
PythonSf ワンライナー
plotTrajectory([(0.9 cos(θ),sin(2θ), θ) for θ in arsq(0, 256,2pi/256)])
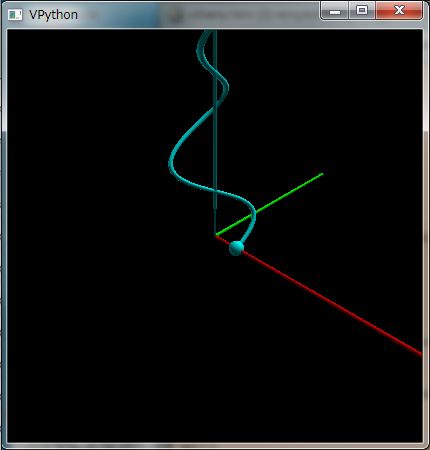
二変数関数:f(x,y) の三次元形状を調べるには plot3DGr(..) を使います。
PythonSf ワンライナー
plot3dGr(sin(`X) cos(`Y), [-pi,pi],[pi,-pi])
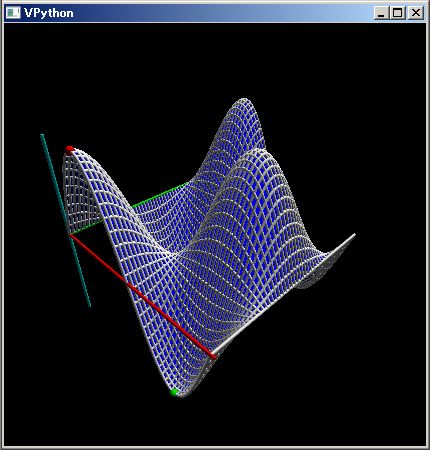
複素平面上の複素数値関数:f(z) の四次元形状:二次元複素平面上の二次元複素数値分布も表示できます。複素数値の絶対値を高さで、その位相回転を RGB 三色の混ざり具合で表示します。
PythonSf ワンライナー
plot3dGr(sin(`X) cos(`X), [-pi,pi],[pi `i,-pi `i])
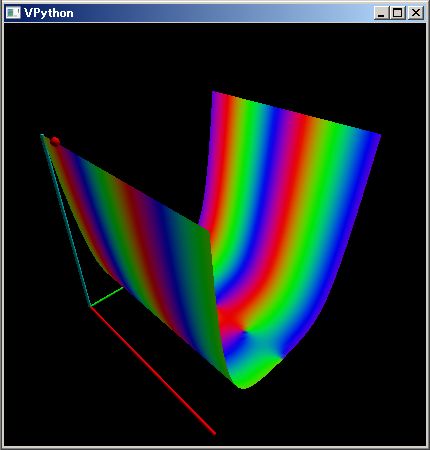
PythonSf ワンライナー
plot3dGr(log, [-pi,pi],[pi `i,-pi `i])
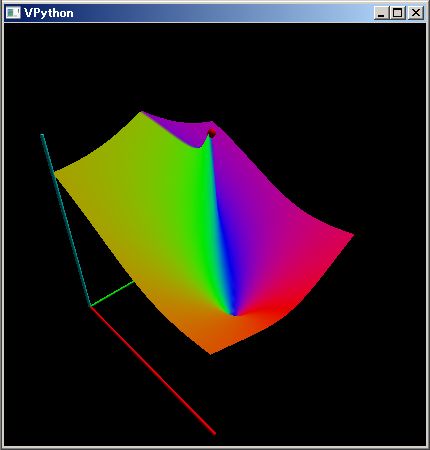
長方形領域での値分布行列を可視化したくなることも多いものです。単なる数値の塊だけでは、値分布の傾向を掴むことは困難です。でも、下のように三次元グラフとして可視化してやれば傾向性を一目で掴めます。
PythonSf ワンライナー
seed(0);vc=~[range(10)]; renderMtrx(vc^vc + 3 randn(10,10))
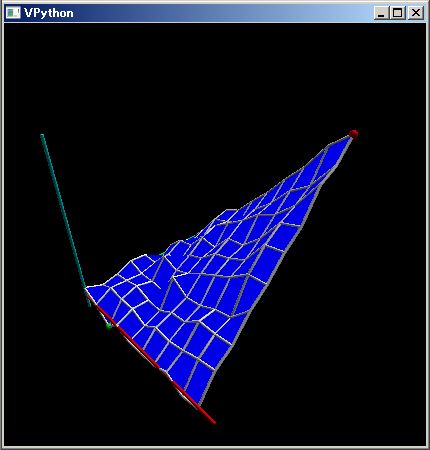
renderMtCplx(..) 関数を使えば、複素数値を要素とする行列の三次元表示ができます。位相回転は RGB の混ざり具合で表します。
PythonSf ワンライナー
seed(0); vc=~[range(10)]; renderMtCplx(vc^vc+3(randn(10,10)+`i randn(10,10)))
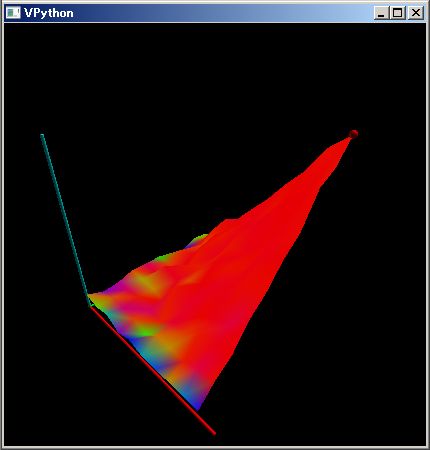
行列要素を三次元の位置ベクトルとする行列値引数を renderFaces(.) 関数に与えてやれば、行列メッシュ平面を そのベクトル要素位置に変換した三次元平面を描画できます。下に例を示します。
PythonSf ワンライナー
# メビウスの帯
dct={}; for idx, (u,v) in enmitr(klsp(0,2pi),klsp(-1,1,10)):dct[idx]=((1+0.5v cos(0.5u))cos(u), (1+0.5v cos(0.5u))sin(u), 0.5v sin(0.5u)); renderFaces(dct,blMesh = True)
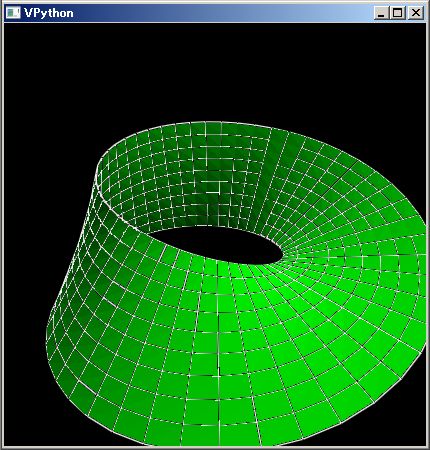
位置ベクトルを要素とするような行列を作るときは、上のように辞書による行列が便利です。あらかじめデータに整合するサイズの行列を宣言する必要がないからです。位置ベクトルを要素とする行列のような面倒なものを考えずに済むからです。
PythonSf ブロック
# クラインの壷
//@@
dct,N,M,r={},64,32,5;
for (u,v), index in zip(masq([0,N,2pi/N], [-1,M+1,2pi/M]), mrng(N,M+1) ):
dct[index]=( (r+cos(u/2) sin(v)-sin(u/2) sin(2v)) cos(u)
,(r+cos(u/2) sin(v)-sin(u/2) sin(2v)) sin(u)
,sin(u/2) sin(v) + cos(u/2) sin(2*v) )
sf.renderFaces(dct, blMesh = True)
sf.drawAxis()
//@@@
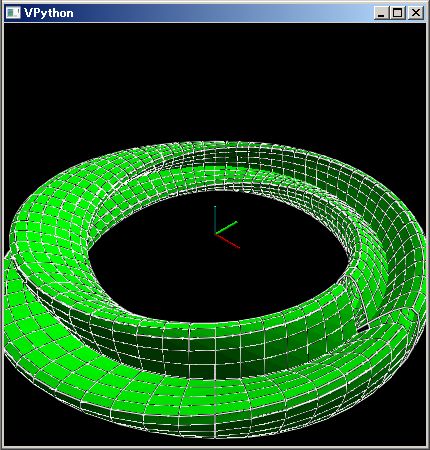
位置ベクトルに加えて RGB カラーベクトル値も要素とする辞書行列を renderFacesWithRGB(.) 関数を与えてやれば、三次元の色つき曲面を描画させられます。下に例を示します。
PythonSf ワンライナー
# 球面調和関数
m,l=0,2;sy();clAt = ClCplxColor();psCl=λ θ,φ:(λ cplxAg=ss.sph_harm(m,l,φ,θ):(abs(cplxAg) ~[sin(θ)cos(φ),sin(θ)sin(φ),cos(θ)], clAt.GetFltColor(0.99 cplxAg/abs(cplxAg))))();dct={};for idx,(θ,φ) in enmitr(klsp(0,pi),klsp(0,2pi)):dct[idx]=psCl(θ,φ);renderFacesWithRGB(dct)
複素数値関数の値分布を表示するために、kkRGB 表示と名付けた複素数値行列の値分布表示関数:render2dRGB(..)を用意しています。
この関数は下の np.info(render2dRGB) にある引数値をとります。mtrxAg は複素数値行列です。この行列要素をピクセル一つづつに対応させ、四角い jpg 画像を作ります。複素数値の位相角に RGB の混ざり具合を対応させ、その絶対値に明度を対応させます。100x100 のような小さな行列では 100 x 100 pixcel の小さな画像になってしまいます。
PythonSf ワンライナー
np.info(render2dRGB)
render2dRGB(mtrxAg, boundary=1.0, limit=10.0, blReverse=False, blBoth=False,
fileName='kkRGB', blDisplay=True, blMax=False)
' Render a complex value distribution with kkRGB color for matrix argument
rendered figure is saved at kkRGB.jpg file as a default
e.g.
vc=klsp(-3,3,300); f=`X^3+`X^2+`X+1; dct={};for idx,(x,y) in enmitr(vc,vc):dct[idx]=f(x+`i y); render2dRGB(dct)
'
===============================
None
`X^3+`X^2+`X+1 多項式の複素数値分布を render2dRGB(..) 関数で表示させて見ましょう。 下のような具合です。(render2dRGB(..) 関数は、Python の Image モジュールを使って mtrxAg データを変換して kkRGB.jpg ファイルをカレント・ディレクトリに作り、それを start 実行します。すなわち jpg 拡張子に OS で関連付けられたプログラムで kkRGB.jpg 画像が表示されます。)
PythonSf ワンライナー
vc=klsp(-3,3,300); f=`X^3+`X^2+`X+1; dct={};for idx,(x,y) in enmitr(vc,vc):dct[idx]=f(x+`i y); render2dRGB(dct)
上の図で中央に分布している三つのぼやけた黒い丸い領域の中心が、多項式 x^3+x^2+x+1 の複素根の位置に対応しています。根の位置で関数値が 0 になるので、その明度も 0 になっています。(この多項式の根は、下の PythonSf 式で求められます。)
PythonSf ワンライナーたち
poly1d([1,1,1,1],variable='x')
===============================
3 2
1 x + 1 x + 1 x + 1
poly1d([1,1,1,1]).roots
===============================
[ -1.00000000e+00+0.j -7.77156117e-16+1.j -7.77156117e-16-1.j]
真ん中の連続的に変化している領域と四色のみで色分けされている領域の境目が、関数値の絶対値が 1 になっているところです。デフォルト引数 boundary=1.0 で絶対値の 1 が指定されいます。
外側の白い領域との境界が、関数値の絶対値が 10 になるところです。この絶対値 10 は、デフォルト引数 limit=10.0 で指定されています。
四色のみで色分けされている領域は絶対値が 1 以上 10 以下ということになります。この四色は、複素平面の実数直線と純虚数直線で区切られた四つの領域に対応します。ですから、赤と黄色の境界は、関数値が正の実数値となる位置であり、黄色と緑の境界は、正の純虚数値となる位置です。なまじ RGB の連続的な変化より、四色の境界分布のほうが複素解析関数の位相の回り方がよく分かると思います。たとえば、複素解析関数の等高線と等位相線は直交することが、上の kkRGB 図より読み取れます。(これは解析関数一般になりたつ性質です。)如何でしょうか。
多項式 x^3+x^2+x+1 の複素数値分布は、下のように plot3dGr(..) 関数でも表示させられます。こっちの方が手っ取り早く表示できるのですが、reder2dRGB(..) のほうが値分布の詳細をイメージしやすいと思います。皆様はいかがでしょうか。
PythonSf ワンライナー
plot3dGr(`X^3+`X^2+`X+1, [-3,3],[3`i,-3`i])
render2dRGB(..) 関数は下のようにマンデルブロ集合の表示にも使えます。
PythonSf ブロック
//@@
N=512;
def check(c,z=0,k=0):
return k>500 and 500 or abs(z) < 2 and check(c,z^2+c,k+1) or k;
dct={};
for idx,(x,y) in enmasq((-2,N,4/N),(2`i,N,-4`i/N)):
dct[idx]=check(x+y);
def convertTo4cplxVl(inAg):
return inAg==500 and 0.1+0j or inAg>30 and 1+0j or inAg>10 and 1j or inAg>5 and -1+0j or -1j
for idx in mrng(N,N):
dct[idx]=convertTo4cplxVl(dct[idx]);
render2dRGB(dct)
//@@@
plotTmCh(.) 関数に行列引数を与えてやれば、行列の各横ベクトルをタイム・チャート・テータとして表示します。下の 1bit D/A converter の動作の様子をタイム・チャートとして表示してみましょう。
ΔΣ DA converter in >= 2**15 --> 1
in < 2**15 --> 0
16 +┌───┐ + ┌──┐ ┌────────┐ 1
→─/─┤Adder ├─→○┤z^-1├┬─┤Digtal 1bit├┬─/───/\/\/\/─┬────
┌─┤ │ -↑└──┘│ │Comparator D/A ││ │
│ -└───┘ └────┘ └────────┘│ ─┴─
│ integrator │ ─┬─ C/s
└─────────────────────────┘ │
┴
Δ Σ =
A:入力 B:intergrator:countor C:output: 1 or -1
下のワンライナーは、上の 1bit D/A converter の A点、B点、C点の変化の様子をシミュレーション計算して、タイムチャートに表示しています。
PythonSf ワンライナー
N=256;f=λ sg,ds,out:(λ dsAg=ds+sg-out*2^15:[sg,dsAg,1 if dsAg>0 else -1])();mt=kzrs(3,N); mt[:,0]=(0,0,0);for i in range(N-1):mt[:,i+1]=f(2^15 sin(2pi i/N),*mt[:,i][1:]);plotTmCh(mt)
PythonSf でのグラフ表示関数はユーザー側でも簡単に実装可能です。Python には pylab のようなグラフ表示パッケージがあるのですから。上に述べたグラフ表示関数も全てソースを公開しています。下のワンライナーで、plotTmCh(..) 関数のソースを見れます。
PythonSf ワンライナー
np.source(plotTmCh)
In file: pysf\vsGraph.py
def plotTmCh(vctMtrxAg):
"""' plot time chart for vector,array or matrix dictionary data
'"""
import pylab as pb
def __plotTmChX(vctMtrxAg):
n = len(vctMtrxAg)
lstYAt = [None]*(2*n)
lstYAt[0::2] = vctMtrxAg
lstYAt[1::2] = vctMtrxAg
lstYAt = [vctMtrxAg[0]]+lstYAt+[vctMtrxAg[-1]]
lstXAt = [None]*(2*(n+1))
lstXAt[0::2] = range(n+1)
lstXAt[1::2] = range(n+1)
maxAt = max(vctMtrxAg)
minAt = min(vctMtrxAg)
pb.plot(lstXAt, lstYAt)
if maxAt != minAt:
lstAxisAt = list(pb.axis())
meanAt = float(maxAt + minAt)/2
lstAxisAt[2] = minAt + (minAt - meanAt)*0.2 # set Y axis min
lstAxisAt[3] = maxAt + (maxAt - meanAt)*0.2 # set Y axis max
pb.axis(lstAxisAt)
assert '__getitem__' in dir(vctMtrxAg)
if isinstance(vctMtrxAg, dict) or '__len__' in dir(vctMtrxAg[0]):
if isinstance(vctMtrxAg, list):
assert not('__getitem__' in dir(vctMtrxAg[0][0]))
colSizeAt = len(vctMtrxAg)
elif isinstance(vctMtrxAg, dict):
lstAt = vctMtrxAg.keys()
lstAt.sort()
shapeAt = lstAt[-1]
shapeAt = (shapeAt[0]+1, shapeAt[1]+1)
assert shapeAt[0]*shapeAt[1] == len(lstAt),\
"dictionary vctMtrxAg index is not alined" + str(objarAg)
krAt = kzrs(shapeAt)
for index in sf.mrng(*shapeAt):
krAt[index] = vctMtrxAg[index]
vctMtrxAg = krAt
colSizeAt = shapeAt[0]
else:
assert isinstance(vctMtrxAg, sf.sc.ndarray)
assert len( vctMtrxAg.shape ) == 2
colSizeAt = vctMtrxAg.shape[0]
for i, elmAt in enumerate(vctMtrxAg):
# don't use subplot(,,0) not to shift upper
pb.subplot(colSizeAt, 1, i+1)
__plotTmChX(elmAt)
else:
__plotTmChX(vctMtrxAg)
pb.show()
===============================
None
グラフ表示関数の実装なんて大変だと思われるかもしれません。でも VPython または Matplotlib パッケージを利用することで、PythonSf のグラフ表示関数は数十行で記述できてしまっています。これらグラフ表示関数は全てソースを公開しています。上で説明した np.source(..) により PythonSf ワン・ライナーを使って、これら表示関数のソースを見れます。それらを改変できます。
必要なグラフ表示機能はユーザーによって異なります。ぜひともユーザー側でのグラフ表示関数の実装にも挑戦してみてください。それらを書き上げたら customize.py または sfCrrntIn.py ファイルに それらを置いてやるだけで、PythonSf 式から利用できるようになります。
Python の数値積分では scipy.integrate.quad が有名です。でも、この quad(..) 関数は、積分値と、その推測誤差の tuple pair を返してくれます。計算誤差まで返してくれるのは、一見良さそうですが、グラフを描かせたりするときは積分値のみを取り出す必要があり、ワンライナーで短く書くには返って不都合です。そのため quadR(..) 関数を実装しています。
また複素数値関数や調和関数の積分も行えるようにしたいので、PythonSf では計算誤差を返さない、積分値のみを返す quadC, quadAn 関数も用意しています。
quadR(実数値関数, 下限、上限) と引数を与えることで数値積分を計算します。下限・上限値には無限大:sy.inf を指定することも可能です。
PythonSf ワンライナーたち
# pi
#∫ sin(x) dx == 2
# 0
quadR(sin, 0,pi)
===============================
2.0
# scipy.integrate quad による積分
sy(); si.quad(sin, 0,pi)
===============================
(2.0, 2.220446049250313e-14)
# ∞ 範囲の積分
# ∞
#∫ exp(-x^2) dx == π^0.5
#-∞
# SciPy の quad(..) であり計算誤差の推定値も含めた計算結果を返す
sy();si.quad(exp(-`X^2), -sy.inf, sy.inf)
===============================
(1.7724538509055159, 1.4202636756658795e-08)
# PythonSf の quadR(..) であり積分値の計算結果のみを返す。誤差は返さない。
quadR(exp(-`X^2), -np.inf, np.inf)
===============================
1.77245385091
# 参考 π^0.5
sqrt(pi)
===============================
1.77245385091
print '%1.20f'%sqrt(pi)
1.77245385090551590000
-------------------------------
None
quadC(複素数値関数, 下限、上限) と引数を与えることで、複素数値関数の数値積分を計算します。
PythonSf ワンライナー
# Fourier Transform function value
~[quadC(exp(2pi `i ν `X) exp(-`X^2), -np.inf, np.inf) for ν in arsq(0,5,1/5)]
===============================
[ 1.77245385+0.j 1.19432452+0.j 0.36539667+0.j 0.05075766+0.j
0.00320135+0.j]
---- ClTensor ----
# Fourier Transform function of exp(-X^2)
F_f=λ f:( quadC(exp(-2pi `i ν `X) exp(-X^2),-np.inf, np.inf) ).real
Waring: don't use assignment at last sentence.We ignore the assignment.
===============================
at 0x0213A070>
not picklable
F_f=λ f:( quadC(exp(-2pi `i f `X) exp(-`X^2),-np.inf, np.inf) ).real;F_f(3)
===============================
1.32810429321e-13
# フーリエ変換された関数の実数値分布のグラフ表示
F_f=λ f:( quadC(exp(-2pi `i f `X) exp(-`X^2),-np.inf, np.inf) ).real; plotGr(F_f,-2,2)
quadAn(.)に、quadAn(複素領域を定義域とする関数, [複素数値のリスト]) 被積分関数と直線で結んだ積分経路を与えることで、その積分経路に沿った積分値を計算します。下に例を示します。
PythonSf ワンライナー
quadAn(log, [1,`i,-1,-`i,1])
===============================
((-1.1102230246251565e-16-6.283185307179586j), 3.238303350943406e-09, 3.238303350943406e-09)
quadAn(log, [1,`i,-1,-`i,1])[0] ~== (-2 pi `i)
===============================
True
quadAn(..) のときは、予測される積分計算誤差も実数部、虚数部ともに返しています。quadR(.),quadC(.) 関数のようには他の式と組み合わせて使われることが少ないからです。
SciPy の integrate パッケージには ode(..) 関数が備わっています。でもこの関数は、時不変な系についても t を明示的に記述せねばならないなど、使い方が少しばかり面倒です。ワン・ライナーでは ode(..) 関数を使えません。
そこで kOde(..) 関数を作りました。大部分の場合で kOde(..) の方が使いやすいでしょう。下のように使います。
PythonSf ワンライナー
np.info(kOde)
kOde(f, x0, t, N=50)
' time independent Runge Kutta integral by scipy.integrate.ode.
kOde(f, x0, t, N=50)
f:a dynamic equation that may return a vector or list
x0: a initial codition value that may be a scalar,vector or list
t: integrating time [0,t]
N: returning data size
f doesn't include t term unlike scpy.integrate.ode(..)
e.g.
kOde(~[-2 `X `Y, -`X], [1,2], 2s`,10)
===============================
[[ 4.63620997e-01 1.86108060e+00]
[ 2.23487176e-01 1.79540724e+00]
[ 1.09764092e-01 1.76345232e+00]
[ 5.44058566e-02 1.74768585e+00]
[ 2.70894588e-02 1.73985328e+00]
[ 1.35187020e-02 1.73594893e+00]
[ 6.75396145e-03 1.73399941e+00]
[ 3.37618618e-03 1.73302515e+00]
[ 1.68817038e-03 1.73253807e+00]
[ 8.44242482e-04 1.73229450e+00]]
---- ClTensor ----
snipped
上の式で ~[-2 `X `Y, -`X] は下の常微分方程式を意味します。
d | x | == | -2 x y | ---(| |) | | dt | y | | -x |
`X, `Y は加減乗除べき乗算が可能な恒等関数であり、~[-2,`X `Y, -`X] はベクトル関数です。
PythonSf ワンライナー
~[-2 `X `Y, -`X](2,3)
===============================
[-12. -2.]
---- ClTensor ----
kOde(..) を使えば、二次元での N 体問題を解くワンライナーを次のように記述できます。D=2 が二次元を意味しています。inV=[....] に設定する初期位置・速度パラメータの数より、粒子数 N が決まります。
getFV(v,i,k) 関数は、位置・速度パラメータ群ベクトル v に対して、 i 番目と k 番目の粒子の間に働く力を求める関数です。(λ r=krry(v[D k:D (k+1)])-krry(v[D i:D (i+1)]):r/norm(r)^3 if norm(r)!=0 else ~[0,0])() は closure 関数の記述と呼び出しです。i 番目と k 番目の粒子の間の距離 r を定める let 文の役割をデフォルト引数機能使って実装しています。λ 式中では assign 文を使えないので、このようなテクニックを使います。
sumFc(v,j) は、位置・速度パラメータ群ベクトル v に対して、j 番目の粒子に働く力を、 getFV(v,j,k) を足し合わせることで求めています。
粒子数 N 個によって変わる軌跡の色を設定するために、複素数の位相による色指定法:ClCplxColor() を使っています。
PythonSf ワンライナー
D=2;inV=[-0.97m`,0.243, 0.97,-0.243, 0,0, 1,1, -0.466m`/s`,-0.432, -0.466,-0.432, 0.932,0.864, 0,0]; N=len(inV)//(2D) ; getFV=λ v,i,k:(λ r=krry(v[D k:D (k+1)])-krry(v[D i:D (i+1)]):r/norm(r)^3 if norm(r)!=0 else ~[0,0])(); sumFc=λ v,j:sum([getFV(v,j,k) for k in range(N) if j!=k]); fnc= λ *v: np.r_[v[D N:],(~[sumFc(v,j) for j in range(N)]).r]; mt=kOde(fnc,inV, 2 s`,400); cl=ClCplxColor(); for k in range(N):plotTrajectory(mt[:,D k:D (k+1)],color=cl.GetFltColor(exp(`i 2pi k/N)))
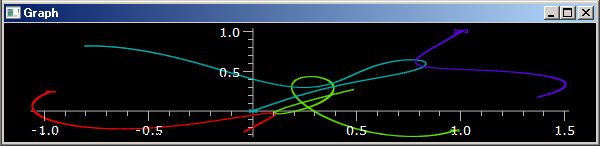
三次元での N 体問題を解くワンライナーは下の様に書けます。
PythonSf ワンライナー
D=3;inV=[-0.97m`,0.243,0, 0.97,-0.243,0, 0,0,1, 1,1,1, -0.466m`/s`,-0.432,0, -0.466,-0.432,0, 0.932,0.864,0, 0,0,0]; N=len(inV)//(2D) ; getFV=λ v,i,k:(λ r=krry(v[D k:D (k+1)])-krry(v[D i:D (i+1)]):r/norm(r)^3 if norm(r)!=0 else ~[0,0])(); sumFc=λ v,j:sum([getFV(v,j,k) for k in range(N) if j!=k]); fnc= λ *v: np.r_[v[D N:],(~[sumFc(v,j) for j in range(N)]).r]; mt=kOde(fnc,inV, 2 s`,400); cl=ClCplxColor(); for k in range(N):plotTrajectory(mt[:,D k:D (k+1)],color=cl.GetFltColor(exp(`i 2pi k/N)))
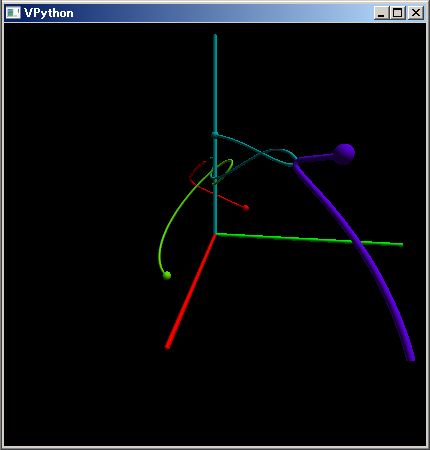
Python Sf における、少し高度な行列演算について説明します。
PythonSf ワンライナー
# ~[ リスト内包表記 ] によるベクトル
~[k^2 for k in range(5)]
===============================
[ 0. 1. 4. 9. 16.]
---- ClTensor ----
# ~[ リスト内包表記 ] による行列生成
~[[k j for k in range(5)] for j in range(4)]
===============================
[[ 0. 0. 0. 0. 0.]
[ 0. 1. 2. 3. 4.]
[ 0. 2. 4. 6. 8.]
[ 0. 3. 6. 9. 12.]]
---- ClTensor ----
# ~[ リスト内包表記 ] による Zp(5) 要素の行列生成
~[[Z5(k j) for k in range(5)] for j in range(4)]
===============================
[[Z5(0) Z5(0) Z5(0) Z5(0) Z5(0)]
[Z5(0) Z5(1) Z5(2) Z5(3) Z5(4)]
[Z5(0) Z5(2) Z5(4) Z5(1) Z5(3)]
[Z5(0) Z5(3) Z5(1) Z5(4) Z5(2)]]
---- ClFldTns:< class 'sfCrrntIni.Z5'> ----
# ~[ リスト内包表記 ] によって生成された、Zp(5) 要素の行列によるベクトルの変換
~[[Z5(k j) for k in range(5)] for j in range(4)] range(3,3+5)
mt=~[[Z5(k j) for k in range(5)] for j in range(4)]; mt range(3,3+5)
===============================
[Z5(0) Z5(0) Z5(0) Z5(0)]
---- ClFldTns:< class 'sfCrrntIni.Z5'> ----
mt=~[[Z5(k j) for k in range(5)] for j in range(4)]; mt range(2,2+5)
===============================
[Z5(0) Z5(0) Z5(0) Z5(0)]
---- ClFldTns:< class 'sfCrrntIni.Z5'> ----
N x M 行列を越えて、N x M x L などの多次元のテンソルも扱えます。それらとベクトルとの積演算も可能です。次のような具合です。
PythonSf ワンライナー
ls=range(3); ~[ [[x+y+z for x in ls] for y in ls] for z in ls]
===============================
[[[ 0. 1. 2.]
[ 1. 2. 3.]
[ 2. 3. 4.]]
[[ 1. 2. 3.]
[ 2. 3. 4.]
[ 3. 4. 5.]]
[[ 2. 3. 4.]
[ 3. 4. 5.]
[ 4. 5. 6.]]]
---- ClTensor ----
PythonSf ワンライナー
# 3x3x3Tensor * 3Vector
ls=range(3); tns=~[ [[x+y+z for x in ls] for y in ls] for z in ls]; tns ls
===============================
[[ 5. 8. 11.]
[ 8. 11. 14.]
[ 11. 14. 17.]]
---- ClTensor ----
PythonSf ワンライナー
# 3Vector * 3x3x3Tensor * 3Vector
ls=range(3); tns=~[ [[x+y+z for x in ls] for y in ls] for z in ls]; ls tns ls
===============================
[ 30. 39. 48.]
---- ClTensor ----
PythonSf ワンライナー
# テンソルどうしの積:Γ`__[j,k,i] Γ`__[i,p,q]
ls=range(3); Γ`__=~[ [[x+y+z for x in ls] for y in ls] for z in ls]; Γ`__ Γ`__
===============================
[[[[ 5. 8. 11.]
[ 8. 11. 14.]
[ 11. 14. 17.]]
[[ 8. 14. 20.]
[ 14. 20. 26.]
[ 20. 26. 32.]]
[[ 11. 20. 29.]
[ 20. 29. 38.]
[ 29. 38. 47.]]]
[[[ 8. 14. 20.]
[ 14. 20. 26.]
[ 20. 26. 32.]]
[[ 11. 20. 29.]
[ 20. 29. 38.]
[ 29. 38. 47.]]
[[ 14. 26. 38.]
[ 26. 38. 50.]
[ 38. 50. 62.]]]
[[[ 11. 20. 29.]
[ 20. 29. 38.]
[ 29. 38. 47.]]
[[ 14. 26. 38.]
[ 26. 38. 50.]
[ 38. 50. 62.]]
[[ 17. 32. 47.]
[ 32. 47. 62.]
[ 47. 62. 77.]]]]
---- ClTensor ----
PythonSf ワンライナー
# Einstein 既約による縮約:Γ`__[j,k,k] Γ`__[m,k,k]
ls=range(3); Γ`__=~[ [[x+y+z for x in ls] for y in ls] for z in ls]; ~[ [sum([Γ`__[j,k,k] Γ`__[m,k,k] for k in ls]) for j in ls] for m in ls]
===============================
[[ 20. 26. 32.]
[ 26. 35. 44.]
[ 32. 44. 56.]]
---- ClTensor ----
テンソル演算は手計算では大変すぎて簡単には扱えませんでした。でも PythonSf を使えば、上のようにテンソル演算も簡単であり実用的に使えます。
スカラー値への ^ 演算子の適用はべき乗演算子の意味でしたが、ベクトルや行列の組への ^ 演算子の適用はダイアディック・ベクトル積などのテンソル演算の意味にしています。下のような具合です。
PythonSf ワンライナー ~[1,2,3]^[4,5,6] =============================== [[ 4. 5. 6.] [ 8. 10. 12.] [ 12. 15. 18.]] ---- ClTensor ---- ~[1,2,3]^~[4,5,6]^~[7,8,9] =============================== [[[ 28. 32. 36.] [ 35. 40. 45.] [ 42. 48. 54.]] [[ 56. 64. 72.] [ 70. 80. 90.] [ 84. 96. 108.]] [[ 84. 96. 108.] [ 105. 120. 135.] [ 126. 144. 162.]]] ---- ClTensor ---- `σx ^ `σz =============================== [[[[ 0. 0.] [ 0. -0.]] [[ 1. 0.] [ 0. -1.]]] [[[ 1. 0.] [ 0. -1.]] [[ 0. 0.] [ 0. -0.]]]] ---- ClTensor ----ベクトルの外積演算は Levi-Civita tensor とベクトルとの積によって計算できます。その他にも複数の方法が使えます。
PythonSf ワンライナーたち # Levi-Civita tensor `εL とベクトルとの積演算による外積 a,b=~[1,2,3],~[4,5,6]; -a `εL b =============================== [-3. 6. -3.] ---- ClTensor ---- # Numpy cross 関数による外積 np.cross([1,2,3],[4,5,6]) =============================== [-3 6 -3] # ^ 演算子による外積 a,b=~[1,2,3],~[4,5,6]; a^b - b^a =============================== [[ 0. -3. -6.] [ 3. 0. -3.] [ 6. 3. 0.]] ---- ClTensor ---- # Wedge 積関数 `Λ(..) による外積 a,b=~[1,2,3],~[4,5,6]; `Λ(a,b) =============================== [[ 0. -3. -6.] [ 3. 0. -3.] [ 6. 3. 0.]] ---- ClTensor ----
三次元だけで使うときは np.cross(..) が良いのかもしれません。
私自身は a^b-b^a や `Λ(a,b) による外積演算が優れていると思います。任意の N 次元ベクトルにも使えるからです。計算結果をベクトルではなくテンソルにしておいたほうが、外積の数学的・物理学的な意味が明確になるからです。このときは三次元ベクトルどうしの外積が 3x3 反対称行列になってしまいますが、こちらの方が本来の数学的・物理学的な意味を表しています。
とくに外積の拡張としての Wedge 積関数:`Λ(..) が微分形式に慣れた方に便利だと思います。任意個数、任意次元のベクトルについて Wedge 積を計算できます。ただし行列を引数としたときまでは実装してありません。誤った計算値になります。御注意ください。
PythonSf ワンライナー
a,b=[1,2,3,4],[5,6,7,8]; `Λ(a,b)
===============================
[[ 0. -4. -8. -12.]
[ 4. 0. -4. -8.]
[ 8. 4. 0. -4.]
[ 12. 8. 4. 0.]]
---- ClTensor ----
a,b,c=[1,2,3,4],[5,6,7,8],[9,10,11,12]; `Λ(a,b,c)
===============================
[[[ 0. 0. 0. 0.]
[ 0. 0. 0. 0.]
[ 0. 0. 0. 0.]
[ 0. 0. 0. 0.]]
[[ 0. 0. 0. 0.]
[ 0. 0. 0. 0.]
[ 0. 0. 0. 0.]
[ 0. 0. 0. 0.]]
[[ 0. 0. 0. 0.]
[ 0. 0. 0. 0.]
[ 0. 0. 0. 0.]
[ 0. 0. 0. 0.]]
[[ 0. 0. 0. 0.]
[ 0. 0. 0. 0.]
[ 0. 0. 0. 0.]
[ 0. 0. 0. 0.]]]
---- ClTensor ----
# 四次元 Zp(3) ベクトルの外積
a,b=~[1,2,3,4,Z3],~[5,6,7,8,Z3]; `Λ(a,b)
===============================
[[Z3(0) Z3(2) Z3(1) Z3(0)]
[Z3(1) Z3(0) Z3(2) Z3(1)]
[Z3(2) Z3(1) Z3(0) Z3(2)]
[Z3(0) Z3(2) Z3(1) Z3(0)]]
---- ClTensor ----
# 下の Pauli 行列の Wedge 積の計算値は誤りです。Wedge 積の引数はベクトルまたはタプル・リストのシーケンス・データのみを想定しています。行列引数はサポートしていません。
`Λ(`σx,`σz)
===============================
[[[[ 0. -1.]
[-1. 0.]]
[[ 1. 0.]
[ 0. -1.]]]
[[[ 1. 0.]
[ 0. -1.]]
[[ 0. 1.]
[ 1. 0.]]]]
---- ClTensor ----
PythonSf の基本関数は加減乗除べき乗算と関数合成が可能です。このような関数を要素とする ClFldTns ベクトルは __call__(..) method を備えており、ベクトル分布関数として扱えます。そのベクトル分布関数は数値微分できます。grad,div,rot を計算できます。次のような具合です。
PythonSf ワンライナー
# ベクトル分布関数
f=~[`X^2 + `Y^2, `X `Y,`Z `X]; f(1,2,3)
===============================
[ 5. 2. 3.]
---- ClTensor ----
# ベクトル分布関数の数値微分インスタンスの (1,2,3) 位置におけるあたい
f=~[`X^2 + `Y^2, `X `Y,`Z `X]; `div(f)(1,2,3)
===============================
4.0
# 3 変数関数の (1,2,3) における grad 数値微分
`grad(λ x,y,z:x^2+y^2+z^2)(1,2,3)
===============================
[ 2. 4. 6.]
# `div(f) が三変数関数であることは分からないので、dim=3 と明示的に指定する。
# λ x,y,z:... ならば三変数引数だと分かるのですが ~[`X ... `Z] 関数では、引数の数が PythonSf には分かりません。
f=~[`X^2 + `Y^2, `X `Y,`Z `X]; `grad(`div(f),dim=3)(1,2,3)
===============================
[ 4.00000000e+00 -1.11022302e-08 0.00000000e+00]
---- ClTensor ----
# rotation
f=~[`X^2 + `Y^2, `X `Y,`Z `X]; `rot(f)(1,2,3)
===============================
[[ 0. 2. -3.]
[-2. 0. 0.]
[ 3. 0. 0.]]
---- ClTensor ----
# Jacobian
f=~[`X^2 + `Y^2, `X `Y,`Z `X]; ∂J(f)(1,2,3)
===============================
[[ 2. 4. 0.]
[ 2. 1. 0.]
[ 3. 0. 1.]]
---- ClTensor ----
rot(..) 関数の結果がベクトルではなく反対称テンソルであることに違和感を抱く方がいるかもしれません。でも敢えて反対称テンソルを返しています。テンソルを返すのならば、二次元や、四次元でも、一般の N 次元でも rot(..) の結果を返せるからです。また反対称テンソルにすることで、rot(..) の数学的・物理的意味が明確になるとも思います。
np.ndarray と ClTensor の加減乗除算は ClTensor インスタンスになります。np.ndarray と ClTensor では乗除算が要素ごとの乗除算になことと、行列・ベクトルの乗除算になる違いがあります。どちらの演算を行っているのか理解して計算を続ける必要があります。
とくに SciPy の 非 ufunc:universal function の行列やベクトルを扱う関数のときに注意が必要です。ClTensor インスタンスを引数として与えても、np.ndarray インスタンスが返ってきてしまうからです。それが嫌で fft バッファ関数を設けたりしています。ufunc ならば ClTensor インスタンスを引数にすれば、ClTensor 値が帰ってくるのですが、SciPy の全ての関数が ufunc に統一されてはいません。
PythonSf は八元数、整数の剰余体:Zp(N), GF(2^8), 置換群:Sn(N) といった代数系も扱えます。一般体の係数からなる多項式も扱えます。その多項式の加減乗除算、整数べき乗算、剰余算も可能です。また ClFldTns クラスは一般の体や環の行列・ベクトル演算も扱えます。これぐらいあれば学部程度(数学課を除く)の代数には十分だと思います。以下これらを見ていきましょう。
これらの代数系のソースは全て公開してあります。興味の有る方はそちらも追ってみてください。できたら御自分に必要な代数系に修正・拡張してみてください。全て Python で書かれている小さなプログラムたちですから簡単です。
素数 p の剰余体:Zp は、整数を素数:p の剰余演算により range(p-1):[0,1, ... ,p-1] の整数に mapping したときに得られる体です。体ですから加減乗除算が可能です。素数 5 に対して %p 演算は下のような性質を持ちます。
PythonSf ワンライナーたち
# 和演算における 3 の逆元
p=5; -3%p
===============================
2
# 整数 0,1, ... , 9 を素数 5 の剰余体に mapping します
p=5; [ x%p for x in range(10)]
===============================
[0, 1, 2, 3, 4, 0, 1, 2, 3, 4]
# 整数 0,1, ... , 9 を素数 5 の剰余体の「和の逆元」に mapping します
p=5; [ (-x)%p for x in range(10)]
===============================
[0, 4, 3, 2, 1, 0, 4, 3, 2, 1]
# 整数 0,1, ... , 9 を素数 5 の剰余体の「積の逆元」に mapping します
p=5; [ (x^(p-2))%p for x in range(10)]
===============================
[0, 1, 3, 2, 4, 0, 1, 3, 2, 4]
# %p が和に対して一貫性があることを確認する
N=10; seed(0); p=5; [ (x%p+y%p)%p==(x+y)%p for x,y in randint(-99,99, size=[N,2])]
===============================
[True, True, True, True, True, True, True, True, True, True]
# %p が積に対して一貫性があることを確認する
N=10; seed(0); p=5; [ ((x%p)*(y%p))%p==(x*y)%p for x,y in randint(-99,99, size=[N,2])]
===============================
[True, True, True, True, True, True, True, True, True, True]
標準配布の sfCrnntIni.py には Z2,Z3,Z4,Z5,Z7 の剰余体/環が定義してあります。上の演算を下のように Z5 で書き直せます。
PythonSf ワンライナーたち
# 和演算における 3 の逆元
-Z5(3)
===============================
Z5(2)
# 整数 0,1, ... , 9 を素数 5 の剰余体に mapping します
[ Z5(x) for x in range(10)]
===============================
[0, 1, 2, 3, 4, 0, 1, 2, 3, 4]
# 整数 0,1, ... , 9 を素数 5 の剰余体の「和の逆元」に mapping します
[-Z5(x) for x in range(10)]
===============================
[0, 4, 3, 2, 1, 0, 4, 3, 2, 1]
# 整数 0,1, ... , 9 を素数 5 の剰余体の「積の逆元」に mapping します
p=5; [ Z5(x)^(p-2) for x in range(10)]
===============================
[0, 1, 3, 2, 4, 0, 1, 3, 2, 4]
# %p が和に対して一貫性があることを確認する
N=10; seed(0); [ Z5(x)+Z5(y)==Z5(x+y) for x,y in randint(-99,99, size=[N,2])]
===============================
[True, True, True, True, True, True, True, True, True, True]
# %p が積に対して一貫性があることを確認する
N=10; seed(0); [ Z5(x)*Z5(y)==Z5(x*y) for x,y in randint(-99,99, size=[N,2])]
===============================
[True, True, True, True, True, True, True, True, True, True]
Zp(N) は体であり、加減乗除算に関連した多くの代数式が実数のときと同じように成り立ちます。例えば 1/a + 1/b == (a+b)/(a b) の等式が 0 ではない任意の Z5 要素についてなりたちます。下の PythonSf 式で実験確認できます。
PythonSf ワンライナー
a,b=Z5(2),Z5(3); 1/a + 1/b == (a+b)/(a b)
===============================
True
PythonSf ワンライナー
N=10; seed(0); [ 1/a + 1/b == (a+b)/(a b) for a,b in ~[randint(1,5, size=[N,2]), Z5] ]
===============================
[True, True, True, True, True, True, True, True, True, True]
Zp(N) は可換体であり、行列演算についても実数のときと同様な代数式が多く成り立ちます。下のように 2x2 行列の逆行列の公式が Z5 でも成り立っていることを実験確認できます。
PythonSf ワンライナー
N=1 ; seed(0); [ 1/~[[a,b],[c,d]] == ~[[d,-b],[-c,a]]/(a d - b c) for a,b,c,d in ~[randint(1,5, size=[N,4]), Z5] ]
===============================
[ClTensor([[ True, True],
[ True, True]], dtype=bool)]
PythonSf ワンライナー
N=4 ; seed(0); [ 1/~[[a,b],[c,d]] == ~[[d,-b],[-c,a]]/(a d - b c) for a,b,c,d in ~[randint(1,5, size=[N,4]), Z5] if a d - b c != 0]
===============================
[ClTensor([[ True, True],
[ True, True]], dtype=bool), ClTensor([[ True, True],
[ True, True]], dtype=bool), ClTensor([[ True, True],
[ True, True]], dtype=bool)]
Zp(N) は要素が有限なので、虱潰しに全部を調べてやることで、上の関係がなりたつことを証明することも可能です。
PythonSf ワンライナー
vc=~[0,1,2,3,4,Z5]; [ 1/~[[a,b],[c,d]] == ~[[d,-b],[-c,a]]/(a d - b c) for a,b,c,d in mitr(vc,vc,vc,vc) if a d - b c != 0]
===============================
[ClTensor([[ True, True],
snip
[ True, True]], dtype=bool), ClTensor([[ True, True],
[ True, True]], dtype=bool)]
Z2,Z3,Z4,Z5,Z7 以外の Zp(N) を使いたいときは oc.Zp(..) 関数を使って Zp(N) クラスをダイナミックに生成させて使います。次のような具合です。
PythonSf ワンライナー
Z11=oc.Zp(11); Z11(5) Z11(6), Z11(10)^10
===============================
( 8, 1)
not picklable
oc.Zp(N) は、関数を呼び出されたとき、ダイナミックに Zp(N) クラスを生成して返しています。ダイナミックなクラスを生成により、任意の N に対して Zp(N) クラスを作れるのですが、その代償としてファイル変数にできなくなります。それを対策するために別に ClZp メタ・クラスを設け、このクラスから Z2,Z3,Z4,Z5,Z7 をクラスをスタティックに生成しています。ただし ClZp メタ・クラスはワン・ライナーでは使いにくいので、適宜使い分けてください。
PythonSf は八元数を扱えます。八元数クラス ClOctonion は octn.py モジュールで定義してあるのですが、標準配布の sfCrrntIni.py ファイルによりグローバル変数 Oc に assign し直してあり、 Oc(...) だけで八元数を生成できます。
八元数は複素数や四元数も含んでいます。この複素数、四元数は加減乗除算に対して閉じています。ですので、Oc(...) の引数に二つの要素だけを指定したときは複素数のような二要素表記になり、上位の六個の 0 要素は八元数値の表記であってもマスクされます。同様に四つの要素で八元数を生成したときは、四要素表記にしてあります。具体的には次のような生成・演算・表記となります。ですから八元数:Oc クラスといっても、Oc(...) は四元数や複素数も対象にできるクラスです。
PythonSf ワンライナーたち
# 八元数の生成
Oc(1,2,3,4,5,6,7,8)
===============================
Oc(1, 2, 3, 4, 5, 6, 7, 8)
# 八元数の積と和
Oc(1,2,3,4,5,6,7,8) Oc(9,0,1,2,3,4,5,6), Oc(1,2,3,4,5,6,7,8)+Oc(9,0,1,2,3,4,5,6)
===============================
(Oc(-124, 20, 32, 44, 24, 60, 80, 76), Oc(10, 2, 4, 6, 8, 10, 12, 14))
# 八元数:複素数の生成
Oc(1,2)
===============================
Oc(1, 2)
# 八元数:複素数の積と和と、比較のための複素数の積
Oc(1,2) Oc(3,4), Oc(1,2)+Oc(3,4), (1+2j) (3+4j)
===============================
(Oc(-5, 10), Oc(4, 6), (-5+10j))
# 八元数:四元数の生成
Oc(1,2,3,4)
===============================
Oc(1, 2, 3, 4)
# 八元数:四元数の積と和
Oc(1,2,3,4) Oc(5,6,7,8), Oc(1,2,3,4)+Oc(5,6,7,8)
===============================
(Oc(-60, 12, 30, 24), Oc(6, 8, 10, 12))
四元数は体ですが積演算の可換性が保証されなくなります。
PythonSf ワンライナー
a,b=Oc(1,2,3), Oc(4,5,6); a b, b a
===============================
(Oc(-24, 13, 18, -3), Oc(-24, 13, 18, 3))
八元数になると結合律が成り立たなくなり、体でさえなくなります。でも逆元は存在しますし、分配率は成り立ちます。
PythonSf ワンライナーたち
# 八元数で結合律が成り立たない例
(Oc(0,1) Oc(0,0,1)) Oc(0,0,0,0,1), Oc(0,1) (Oc(0,0,1) Oc(0,0,0,0,1))
===============================
(Oc(0, 0, 0, 0, 0, 0, 0, 1), Oc(0, 0, 0, 0, 0, 0, 0, -1))
# 八元数でも逆元が存在することの確認実験
N=10; seed(0);[ (Oc(x) Oc(x)^-1) ~== 1 for x in randn(N,8)]
===============================
[True, True, True, True, True, True, True, True, True, True]
# 八元数でも分配率が成り立つことの確認実験
N=10; seed(0);[ (a (b+c)) ~== (a b + a c) for a,b,c in randn(N,3,8)]
===============================
[True, True, True, True, True, True, True, True, True, True]
バイト値に対して加減乗除べき乗算を可能にする GF(2^8) 有限体を pysf\octn.py モジュールで RS クラスとして実装してあります。その原始多項式は、CD や DVD での Reed-Solomon Code で使われているものを使っています。下のような具合の加減乗除べき乗算になります。
PythonSf ワンライナー
np.info(oc.RS)
RS(inAg)
' GF(2^8) for primitive polynomial:x^8 + x^4 + x^3 + x^2 + 1:0x1d
RS.m_lstPwrStt has power values
e.g;; oc.RS.m_lstPwrStt
[1, 2, 4, 8, 16, 32, 64, 128, 29, 58, ... 173, 71, 142]
oc.RS(0x12) + oc.RS(0x43)
===============================
0x51
oc.RS(0x12) - oc.RS(0x43)
===============================
0x51
oc.RS(24) oc.RS(31)
===============================
0x15
oc.RS(24)/oc.RS(31)
===============================
0xd7
oc.RS(2)^8
===============================
0x1d
oc.RS(2)^-8
===============================
0x83
RS インスタンスは RS(2) のべき乗整数インデックスが m_lsPwrStt リスト・データ・メンバーに作ってあります。このインデックスは RS の世界での指数とみなせます。RS の乗除算は、この指数を使って実装してあります。
PythonSf ワンライナー
oc.RS.m_lstPwrStt.index(24)
===============================
28
oc.RS.m_lstPwrStt.index(31)
===============================
113
hex(oc.RS.m_lstPwrStt[28+113])
===============================
0x15
np.source(oc.RS.__mul__)
In file: pysf\octn.py
def __mul__(self, inAg):
if isinstance(inAg,RS):
inAg = inAg.m_val
elif isinstance(inAg, (int, long)):
pass
else:
# inAg may be ClFldTns
return inAg.__rmul__(self)
if (inAg % 256 == 0):
return RS(0)
if self.m_val == 0:
return RS(0)
idxLeftAt = RS.m_lstPwrStt.index(self.m_val)
idxRightAt = RS.m_lstPwrStt.index(inAg % 256)
return RS(RS.m_lstPwrStt[(idxLeftAt + idxRightAt)%255])
===============================
None
np.source(oc.RS.inv)
In file: pysf\octn.py
def inv(self):
"""' Return inverse instance '"""
if self.m_val % 256 == 0:
raise ZeroDivisionError("0 divition at inv(.)")
idxAt = RS.m_lstPwrStt.index(self.m_val)
return RS( RS.m_lstPwrStt[(-idxAt) % 255] )
===============================
None
oc.RS インスタンスを要素とする行列やベクトルも、下のように殆ど数値のときと同様に扱えます。Reed-Solomon 符号などを考えるとき oc.RS は便利に使えます。(このような行列・ベクトル演算ができるからこそ、エラー訂正のアルゴリズムが構築できています)
PythonSf ワンライナーたち
# oc.RS インスタンスを要素とする 2x2 行列
~[ [1,2],[3,4], oc.RS]
===============================
[[0x01 0x02]
[0x03 0x04]]
---- ClFldTns:< class 'pysf.octn.RS'> ----
# oc.RS インスタンスを要素とする、長さ 2 のベクトル
RS=oc.RS; ~[RS(5), RS(6)]
===============================
[0x05 0x06]
---- ClFldTns:< class 'pysf.octn.RS'> ----
# oc.RS インスタンスでの行列とベクトルの積
RS=oc.RS; mt,vc = ~[RS(5), RS(6)],~[ [1,2],[3,4], RS]; mt vc
===============================
[0x0f 0x12]
---- ClFldTns:< class 'pysf.octn.RS'> ----
# oc.RS インスタンスでの逆行列
~[ [1,2],[3,4], oc.RS]^-1
===============================
[[0x02 0x01]
[0x8f 0x8e]]
---- ClFldTns:< class 'pysf.octn.RS'> ----
Z2 とは独立して、ブール体クラス BF を pysf\ocnt.py モジュールに実装してあります。ブール体を使う頻度は高いので customize.py で `1,`0 に BF(1),BF(0) インスタンスを対応させてあります。
PythonSf ワンライナーたち
type(`1)
===============================
np.info(oc.BF)
BF(inAg)
' Bool Field: data member is 1 or 0
`1 * `0 = `0 # and
`1 * `1 = `1
`0 * `0 = `0
`1 + `0 = `1 # xor
`1 + `1 = `0
`0 + `0 = `0
'
Methods:
inv -- ' inverse BF(1) '
===============================
None
結合律は意外と強力です。下のように演算表の一行目が与えられただけで、群でもないのに他の行が定まってしまいます。このことの確認はコンピュータの助けがないと相当困難だと思います。
0 1 2 3
0 [1,3,0,1],
1 [?,?,?,?],
2 [?,?,?,?],
3 [?,?,?,?]
演算表の一行目は 0*? を定めています。これから (0*0)*?, (0*(0*0))*? が定まります。演算表の3列が埋まります。
PythonSf ワンライナーたち
# given first row
v=[1,3,0,1]; [v[k] for k in range(4)]
===============================
[1, 3, 0, 1]
# 0*x : 0*0, 0*1, 0*2, 0*3
v=[1,3,0,1]; [v[v[k]] for k in range(4)]
===============================
[3, 1, 1, 3]
# (0*0)*x : 1*0, 1*1, 1*2, 1*3
v=[1,3,0,1]; [v[v[v[k]]] for k in range(4)]
===============================
[1, 3, 3, 1]
# (0*(0*0))*x : 3*0, 3*1, 3*2, 1*3
v=[1,3,0,1]; [v[v[v[v[k]]]] for k in range(4)]
===============================
[3, 1, 1, 3]
0 1 2 3
0 [1,3,0,1],
1 [3,1,1,3],
2 [?,?,?,?],
3 [1,3,3,1]
0*? の一行のデータから演算表の三行まで決まってしまいました。残りの一行は定まらないのでしょうか?
結合律は、2*? の行も限定してしまいます。2*? に与えられたデータも結合律より他の行も定める可能性が高いからです。2*? が定める他の行が既存の三行と矛盾しないものしか許されないからです。下の PythonSf ブロック・コードから、この矛盾しない一行を brute force に求められます。[0,1,2,3] と [3,1,2,3] の二つしか許されません。
PythonSf ブロック
//@@
mt=~[[1,3,0,1],
[3,1,1,3],
[0,0,0,0],
[1,3,3,1]]
l4=range(4)
for v in mitr(*[l4]*4):
mt[2,:]=v
if all([ mt[i,mt[j,k]] == mt[mt[i,j],k] for i,j,k in mitr(*[l4]*3)]):
print v
//@@@
(0, 1, 2, 3)
(3, 1, 2, 3)
実際に、この二つとも (x y) z == x (y z) の関係式を全ての組み合わせで満たしていることを下の PythonSf ワンライナーで確認できます。
PythonSf ワンライナーたち
mt=~[[1,3,0,1], [3,1,1,3], [0,1,2,3], [1,3,3,1]] ; ls=range(4); all([ mt[i,mt[j,k]] == mt[mt[i,j],k] for i,j,k in mitr(ls,ls,ls)] )
===============================
True
mt=~[[1,3,0,1], [3,1,1,3], [3,1,2,3], [1,3,3,1]] ; ls=range(4); all([ mt[i,mt[j,k]] == mt[mt[i,j],k] for i,j,k in mitr(ls,ls,ls)] )
===============================
True
結合律の、この粘着性:一箇所を定めるだけで他の多くも定まってしまうのは凄いと思います。この凄さは自分の手で具体例を扱ってみないと体感できないと思います。そして、この体感のためには、普通の人間はコンピュータの力を借りなければなりません。ただし通常のプログラム言語を使ったのではデバッグ作業に手間をとられすぎて、たいして役に立たないと思います。Matlab や Mathematica でも、こんな計算をやりたくないと思います。Mathematical Scripting Language PythonSf が必要だと思います。
ちなみに Category Theory は、集合論に結合律の構造を入れたものだとみなせます。Category Theroy を有用なものにしているのは、この結合律の粘着性だと思います。皆様はどのように考えますでしょうか。
高校数学で出てくる整数・実数・複素数係数の多項式は Numpy の poly1d クラスで扱うのが便利です。下のような計算ができます。
PythonSf ワンライナーたち
# 多項式インスタンスの生成
p=np.poly1d; p([1,2,3,4])
===============================
3 2
1 x + 2 x + 3 x + 4
# 多項式インスタンスどうしの割り算
p=np.poly1d; p([1,2,3,4])/p([4,5,6])
===============================
(poly1d([ 0.25 , 0.1875]), poly1d([ 0.5625, 2.875 ]))
# 一次単項多項式 x の定義と、その演算
p=np.poly1d; x=p([1,0]); (x^3+ 4 x^2 + 5)^2
===============================
6 5 4 3 2
1 x + 8 x + 16 x + 10 x + 40 x + 25
# 項多項式の微分
p=np.poly1d; x=p([1,0]); (x^3+ 4 x^2 + 5).deriv()
===============================
2
3 x + 8 x
# 多項式の積分
p=np.poly1d; x=p([1,0]); (x^3+ 4 x^2 + 5).integ()
===============================
4 3
0.25 x + 1.333 x + 5 x
p=np.poly1d; x=p([1,0]); ((x^3+ 4 x^2 + 5)^2 /(x^2+x+1))
===============================
(poly1d([ 1., 7., 8., -5., 37.]), poly1d([-32., -12.]))
# 多項式割り算の商
p=np.poly1d; x=p([1,0]); ((x^3+ 4 x^2 + 5)^2 /(x^2+x+1))[0]
===============================
4 3 2
1 x + 7 x + 8 x - 5 x + 37
# 多項式の根
p=np.poly1d; p([1,2,3,4]).roots
===============================
[-1.65062919+0.j -0.17468540+1.54686889j -0.17468540-1.54686889j]
# 複素数係数の多項式
p=np.poly1d; p([1,2+5j,3,4])
===============================
3 2
1 x + (2 + 5j) x + 3 x + 4
# 複素数係数の多項式の根
p=np.poly1d; p([1,2+5j,3,4]).roots
===============================
[-1.73932579-5.4296024j 0.32545721+0.88631641j -0.58613142-0.45671402j]
# 一次単項多項式 x で定義した関数のグラフ
p=np.poly1d; x=p([1,0]); f=(x^3+ 4 x^2 + 5)^2; plotGr(f, -5,2)
学部数学になると Zp(N) など様々の可換体の値を係数とする多項式を扱う必要がでてきます。np.poly1d では、そんなのは扱えません。PythonSf では pysf\octn.py モジュールに一般体係数の多項式クラス Pl が定義してあるので、Zp(N) などの可換体係数多項式を扱えます。下のような具合です。
PythonSf ワンライナー
np.info(oc.Pl)
Pl(*sqAg, **kwDctAg)
' polynomial for algebraic coefficients
usages:
import octn as oc
oc.Pl(1,2,3,4) # a integer coefficient polynomial
=============================== # int type is estimated from paramters
1x^3+2x^2+3x+4
lst=[1,2,3,4];oc.Pl(lst) # can use sequence argment too
===============================
1x^3+2x^2+3x+4
oc.Pl(1,2,3,4, variable='D') # assign polynomial variable string
===============================
1D^3+2D^2+3D+4
oc.Pl(1,2,3,4, oc.BF) # assgin bool field coefficient
===============================
x^3+x # 0 suppressed
oc.Pl(1,2,3,4, dtype=oc.BF) # assgin bool field coefficient with dtype key word
===============================
x^3+x
oc.Pl(1,2,3,`1) # assign type estimating from argments
=============================== # ;;type(sum([1,2,3,`1])) #== oc.BF
x^3+x+1
P=oc.Pl; P([1,2,3,4],Z3)
===============================
Z3(1)x^3+Z3(2)x^2+Z3(1)
P=oc.Pl; P([5,6,7,8],Z3)
===============================
Z3(2)x^3+Z3(1)x+Z3(2)
P=oc.Pl; P([1,2,3,4],Z3) + P([5,6,7,8],Z3) # add
===============================
Z3(2)x^2+Z3(1)x
P=oc.Pl; P([1,2,3,4],Z3) - P([5,6,7,8],Z3) # subtract
===============================
Z3(2)x^3+Z3(2)x^2+Z3(2)x+Z3(2)
P=oc.Pl; P([1,2,3,4],Z3) * P([5,6,7,8],Z3) # multiply
===============================
Z3(2)x^6+Z3(1)x^5+Z3(1)x^4+Z3(1)x^2+Z3(1)x+Z3(2)
P=oc.Pl; P([1,2,3,4],Z3) / P([5,6,7,8],Z3) # divide and (quotient,residual)
===============================
(Pl(Z3(2)), Pl(Z3(2)x^2+Z3(1)x))
P=oc.Pl; P([1,2,3,4],Z3) % P([5,6,7,8],Z3) # residual
===============================
Z3(2)x^2+Z3(1)x
P=oc.Pl; P([1,2,3,4],Z3) // P([5,6,7,8],Z3) # quotient
===============================
Z3(2)
P=oc.Pl; P([1,2,3,4],Z3)^3 # exponent
===============================
Z3(1)x^9+Z3(2)x^6+Z3(1)
P=oc.Pl; P([1,2,3,4],Z3)(P([5,6,7,8],Z3)) # composition
===============================
Z3(2)x^9+Z3(2)x^6+Z3(2)x^4+Z3(2)x^3+Z3(2)x^2+Z3(2)x+Z3(2)
CRC 多項式など、ブール体係数の多項式は使う頻度が高いので、 customize.py の中で oc.Pl を継承したブール体専用の多項式クラス PB を定義してあり、それを使って `P ラベルに単項一次式を割り当ててあります。
PythonSf ワンライナーたち
type(`P)
===============================
<class 'pysf.customize.PB'>
np.source(PB)
In file: pysf\customize.py
class PB(oc.Pl):
"""' BF:Bool Field `P polynomial '"""
def __init__(self, *sqAg):
oc.Pl.__init__(self, dtype = oc.BF, variable='`P', *sqAg)
===============================
None
`P を使うことで、教科書に書いてある多くのブール体系数多項式をエディタ上で計算できるようになります。
PythonSf ワンライナーたち
# ブール体係数多項式における商と余りの計算
(`P^5+1)/(`P+1)
===============================
(Pl(`P^4+`P^3+`P^2+`P+1), Pl(0))
# ブール体係数多項式における商の計算
(`P^5+1)//(`P+1)
===============================
`P^4+`P^3+`P^2+`P+1
# ブール体係数多項式における剰余の計算
(`P^5+1)%(`P^2+1)
===============================
`P+1
`P を使えば、`P^3+`P+1 ブール体係数多項式が既約多項式であること、すなわち 1 以外の多項式では割り切れないことを下のように虱潰し法によって証明できます。
PythonSf ワンライナー
# `P^3+`P+1 が既約多項式であることの虱潰し証明
# 二次までのブール体係数多項式全ての内から(0 を除く)、剰余多項式が 0 になるものを列挙する ==> 1 のみ
ls=[`0,`1]; [ x for x in mitr(*[ls]*3) if PB(x) !=0 and (`P^3+`P+1)%PB(x) ==0]
===============================
[(BF(0), BF(0), BF(1))]
Python には builtin itertools モジュールがあり無限長シーケンスを扱えます。でも それは無限繰り返し処理のためのモジュールであり、無限長数列のためのモジュールではありません。ですから unsubscriptable であり、数列を扱うのに必須な [..] によるインデックスを使えません。
でも [..] によるインデックスは __getitem__(..) を実装するだけで使えるようになります。itertools の各クラスには __iter__(..) method が実装されており、それを少し変形して __getitem__(..) method を実装できます。そのような wrapper クラス tn.idx を pysf\tlRcGn.py に実装してあります。 itertools の各クラスは、この tn.idx wrapper で包み直すことで、[..] によるインデックスを使って遅延評価で各要素をアクセスできるようにしてあります。なお pysf.tlRcGn モジュールは tn のラベルに割り当ててあります。これにより次のような無限長数列の PythonSf 式計算が可能になります。
PythonSf ワンライナー
np.info(tn)
'
extended itertools usages:
tn.count(3)[1:10]
===============================
[4, 5, 6, 7, 8, 9, 10, 11, 12]
(tn.imap(lambda x:x^2, tn.count(10) )[1:10])
===============================
[121, 144, 169, 196, 225, 256, 289, 324, 361]
tn.cycle(xrange(3))[1:10]
===============================
[1, 2, 0, 1, 2, 0, 1, 2, 0]
tn.repeat('s',100)[1:10]
===============================
['s', 's', 's', 's', 's', 's', 's', 's', 's']
tn.repeat(True)[1:10]
===============================
[True, True, True, True, True, True, True, True, True]
tn.repeat(`1)[1:10]
===============================
[BF(1), BF(1), BF(1), BF(1), BF(1), BF(1), BF(1), BF(1), BF(1)]
tn.izip(range(100), xrange(3,100))[1:10]
===============================
[(1, 4), (2, 5), (3, 6), (4, 7), (5, 8), (6, 9), (7, 10), (8, 11), (9, 12)]
tn.izip(range(100), xrange(3,100), tn.count() )[1:10]
===============================
[(1, 4, 1), (2, 5, 2), (3, 6, 3), (4, 7, 4), (5, 8, 5), (6, 9, 6), (7, 10, 7), (8, 11, 8), (9, 12, 9)]
(tn.ifilter(lambda x:x%2==0, tn.count(10) )[1:10])
===============================
[12, 14, 16, 18, 20, 22, 24, 26, 28]
(tn.ifilter(None, tn.count() )[1:10])
===============================
[2, 3, 4, 5, 6, 7, 8, 9, 10]
(tn.ifilterfalse(lambda x:x%2==0, tn.count(10) )[1:10])
===============================
[13, 15, 17, 19, 21, 23, 25, 27, 29]
(tn.ifilterfalse(None, tn.count() )[0])
===============================
0
tn.islice(tn.count(),1,30,3 )[3:10]
===============================
[10, 13, 16, 19, 22, 25, 28]
tn.startmap(lambda *tplAg:sum(tplAg), tn.izip(range(15), range(3,100)) )[1:10]
===============================
[5, 7, 9, 11, 13, 15, 17, 19, 21]
'
===============================
None
pi/4 == 1 - 1/2 + 1/5 - 1/7 + ... + (-1)^n 1/(2n+1) ... の公式を使って、少し PythonSf の tn の itertools で遊んでみましょう。
PythonSf ワンライナーたち
# pi/4 となる無限長数列のインデックス 10 までの数列
# 下で `1r は sympy の有理数の 1 です。これにより分数表記にできます。
ts(); tn.imap(λ n:(-`1r)^n 1/(2n+1), tn.count() )[:10]
===============================
[1, -1/3, 1/5, -1/7, 1/9, -1/11, 1/13, -1/15, 1/17, -1/19]
# 上の無限長数列のインデックス 50 までの和
# 数列要素が有理数なので、その級数和も有理数になります。
ts(); sum(tn.imap(λ n:(-`1r)^n 1/(2n+1), tn.count() )[:50])
===============================
850151369116051611488718369170287588082/1089380862964257455695840764614254743075
# pi/4 と、上の無限長数列のインデックス 50 までの和の浮動小数点値
ts(); pi/4, float(sum(tn.imap(λ n:(-`1r)^n 1/(2n+1), tn.count() )[:50]))
===============================
(0.7853981633974483, 0.7803986631477526)
# atan(.) の 1 における厳密値
ts(); ts.atan(1)
===============================
pi/4
#atan の Taylor 展開
ts(); ts.series(ts.atan(`x),`x,n=20)
===============================
x - x**3/3 + x**5/5 - x**7/7 + x**9/9 - x**11/11 + x**13/13 - x**15/15 + x**17/17 - x**19/19 + O(x**20)
Python は開かれた言語です。パッケージやモジュールを import することで、数値計算の他にも多様な処理が可能になります。それらの多くはワンライナーで実行可能です。以下それらの便利な処理を見ていきましょう。
短い Python コードをテスト実行したくなることがよくあります。Python の全てを頭の中に入れるのは無理だからです。皆様は Python で下のように書けるのをご存知でしょうか。これらの動作結果をデバッガなどを立ち上げることなく、思いつくままにエディタ上で確認できてしまいます。
PythonSf ワンライナーたち
# == 演算子の一括比較
a,b,c=1+1,2+0,3-1; a==b==c
===============================
True
# != の一括比較は無理
a,b,c=1+1,2+0,3+1; a!=b!=c
===============================
False
# <= 演算子の一括比較
a,b,c=1 ,2 ,3 ; a<=b<=c
===============================
True
PythonSf ワンライナー
# 整数/実数の hash 値
x=124; hash(x), hash(124.0),hash(124.1)
===============================
(124, 124, -924195431)
PythonSf ワンライナーたち
# ベクトルのリストのような和 1
np.r_[~[1,2,3],~[4,5,6,7]]
===============================
[ 1. 2. 3. 4. 5. 6. 7.]
# ベクトルのリストのような和 2
np.r_[np.array([1,2,3]), 0, 0, np.array([4,5,6])]
===============================
[1 2 3 0 0 4 5 6]
# ellipsis 演算: ...
arange(3*4).reshape(3,4)[..., :2]
===============================
[[0 1]
[4 5]
[8 9]]
PythonSf ワンライナーたち
# 実数に対する %,// 演算
pi%1
===============================
0.14159265359
pi//1
===============================
3.0
# 負の実数に対する %,// 演算
-2.345% 1
===============================
0.655
-2.345//1
===============================
-3.0
# 複素数では、虚数側は元の値のまま
(pi+`i 3.456 )%1
===============================
(0.14159265359+3.456j)
予定を検討するときなどで特定月のカレンダーを見たいことが良くあります。PythonSf があれば、次のワン・ライナーで指定した年月の曜日を打ち出せます。
PythonSf ワンライナー
import calendar as cl; cl.prmonth(2011, 8)
August 2011
Mo Tu We Th Fr Sa Su
1 2 3 4 5 6 7
8 9 10 11 12 13 14
15 16 17 18 19 20 21
22 23 24 25 26 27 28
29 30 31
===============================
None
予定表も書き込めるカレンダーを欲しいときは、下のように w,l のキーワード引数に空き幅を指定します。
import calendar as cl; cl.prmonth(2011, 8, w=11, l=2)
August 2011
Monday Tuesday Wednesday Thursday Friday Saturday Sunday
1 2 3 4 5 6 7
8 9 10 11 12 13 14
15 16 17 18 19 20 21
22 23 24 25 26 27 28
29 30 31
===============================
None
毎月の業務メモのテンペレートの一行目に、このカレンダー・ワンライナーを置いておくのも便利ではないでしょうか。
python には zipfile, tarfile といったファイルの圧縮・解凍のための package が備わっています。それらを利用すれば、エディタ上でファイルの圧縮・解凍操作が可能です。
# 雛形
import tarfile as tr;tr.open('', 'r').extractall()
import tarfile as tr;tr.open('', 'r').list()
import tarfile as tr;tr.open('D:/lng/msysgit/bin/sfepy/gmsh/gmsh-2.5.0-source.tgz', 'r').list()
# 解凍 ワン・ライナーの例
import tarfile as tr;tr.open('D:/lng/msysgit/bin/sfepy/gmsh/gmsh-2.5.0-source.tgz', 'r').extractall()
# 雛形;;ss='';import tarfile as tr;tr.open(ss, 'r').list()
ss='D:/lng/msysgit/bin/sfepy/gmsh/gmsh-2.5.0-source.tgz';import tarfile as tr;tr.open(ss, 'r').list()
Vi Rs Vx
───|>|-─MWMW───┬───┐
│ │
─┴─ ≧
─┬─ C ≦Rl
│ │
───────────┴───┘
上のようなシリーズ・レギュレータ回路の電流・電圧値を正確に計算した経験のある方は少ないと思います。整流ダイオードのために系が非線形なってしまい、まともに取り扱うのが面倒だからです。でも常微分方程式のソルバー: kOde(..) を使えば、下のように簡単に計算できてしまいます。
電圧 Vi,Vx と抵抗、コンデンサの間には下のような関係があります。
関係式
C dVx/dt = (Vi-Vx)/Rs - Vx/Ri if Vi > Vx
C dVx/dt = - Vx/Ri if Vi < Vx
dVx/dt = ((Vi-Vx)/Rs - Vx/Rl)/C if Vi > Vx
dVx/dt = ( - Vx/Rl)/C if Vi < Vx
これだけ分っていれば、kOde(..) で上の系の挙動をシミュレーション計算できます。
PythonSf ワンライナー
# 出力電圧:Vx
sy(); f0=50Hz`; f=7V` absF(sin(2pi f0 `T)); C,Rs,Rl=1000uF`, 1Ω`,33Ω`;mt=kOde(λ t,Vx:[1,((f(t)-Vx)/Rs-Vx/Rl)/C if f(t)>=Vx else (-Vx/Rl)/C],[0,0],100ms`,256); plotGr(mt[:,1])
PythonSf ワンライナー
# 入力電流
sy(); f0=50Hz`; f=7V` absF(sin(2pi f0 `T)); C,Rs,Rl=1000uF`, 1Ω`,33Ω`;mt=kOde(λ t,Vx:[1,((f(t)-Vx)/Rs-Vx/Rl)/C if f(t)>=Vx else (-Vx/Rl)/C],[0,0],100ms`,256); plotGr([(f(t)-Vx)/Rs if f(t)>=Vx else 0 for t,Vx in mt])
PythonSf ワンライナー
# 入力電流:Vi と出力電圧:Vx
sy(); f0=50Hz`; f=7V` absF(sin(2pi f0 `T)); C,Rs,Rl=1000uF`, 1Ω`,33Ω`;mt=kOde(λ t,Vx:[1,((f(t)-Vx)/Rs-Vx/Rl)/C if f(t)>=Vx else (-Vx/Rl)/C],[0,0],100ms`,256); plotGr([(f(t)-Vx)/Rs if f(t)>=Vx else 0 for t,Vx in mt]);plotGr(mt[:,1],color=red)
縦軸が電圧値と電流値の両方を兼ねています。単位が異なります。物理的には許されません。でも自分だけが見るグラフならば、意味が分っていますから許されるでしょう。
PythonSf ワンライナー
# 最大突入電流:Vi
sy(); f0=50Hz`; f=7V` absF(cos(2pi f0 `T)); C,Rs,Rl=1000uF`, 1Ω`,33Ω`;mt=kOde(λ t,Vx:[1,((f(t)-Vx)/Rs-Vx/Rl)/C if f(t)>=Vx else (-Vx/Rl)/C],[0,0],100ms`,256); plotGr([(f(t)-Vx)/Rs if f(t)>=Vx else 0 for t,Vx in mt])
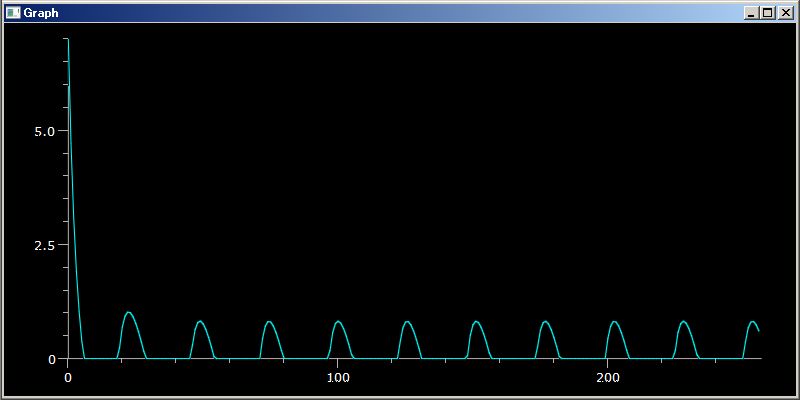
最大突入電流を計算するため、入力電圧関数を sin(.) ではなく cos(.) にしました。
シリコンの 0.6V 分も含めた計算も簡単です。λ式を二重に使い、キーワード引数を O'Caml などの let 文の代わりにしています。
PythonSf ワンライナー
sy(); f0=50Hz`; f=λ t:(λ v=7V` cos(2pi f0 t):v-0.6V` if v>0.6V` else 0)(); C,Rs,Rl=1000uF`, 1Ω`,33Ω`;mt=kOde(λ t,Vx:[1,((f(t)-Vx)/Rs-Vx/Rl)/C if f(t)>=Vx else (-Vx/Rl)/C],[0,0],100ms`,256); plotGr([(f(t)-Vx)/Rs if f(t)>=Vx else 0 for t,Vx in mt])
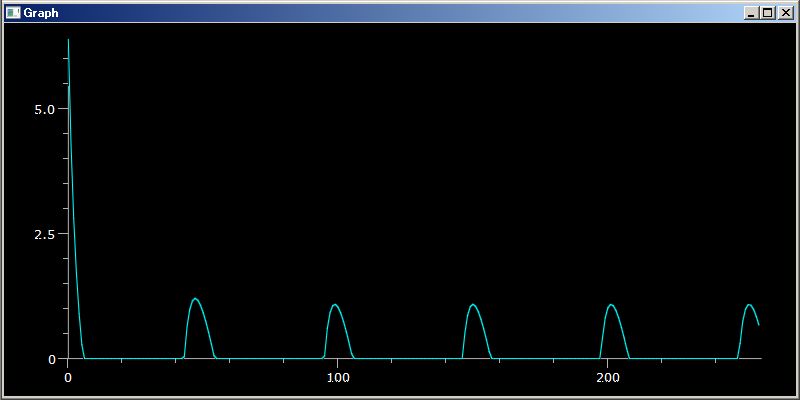
歯車を PythonSf で描いてみました
描く歯車の仕様は ここで定義されている小歯です。歯車のインボリュート曲線の扱い方は、ここの説明を基にしました。ただし、この説明では、基準円の位置における「歯みぞの幅」と「円弧歯厚」の比率を幾つにするかが書いてありませんので両者を同じとしました。
PythonSf ワンライナーたち
# 歯みぞ部分の中心角と弦長
ts(); m,αpressure,z,d,db=3mm`,20degree`,12,36mm`,33.829mm`; rb=db/2; invα=tan(αpressure)-αpressure;θtoothBaseRootAngle=2pi/(2z)-2invα; θtoothBaseRootAngle, 2rb sin(θtoothBaseRootAngle/2)
===============================
(0.231990620064706, 0.00391521173663291*m`)
# 歯末のたけ 2.5mm を 0.00391521173663291*m` の弦に対して実現する 半径と角度
<== 0.00215788829426498*m`, 2.27309298984rad`
2 r sin(θ/2) == 0.00391521173663291*m`
r-r cos(θ/2) == r(1-cos(θ/2))== 2.5mm`
== (1-cos(θ/2)) 0.00391521173663291*m`/(2 sin(θ/2))
ts(); 2.5mm`/(0.00391521173663291*m`)
===============================
0.638535069919361
θ=`X; plotGr((1-cos(θ/2)) /(sin(θ/2))- 0.638535069919, 0, pi)
<== 見た目 θ == 2.28 rad` で上の関係式を満たす
# より厳密には下の角度で 上の関係式を満たす
θ=`X; invF((1-cos(θ/2)) /(sin(θ/2))- 0.638535069919,0.1, 3)(0)
===============================
2.27309298984
上で計算された追加パラメータを加えて、下のように平歯車を描かせました。
PythonSf ブロック
//@@
d=36mm` # pitch diameter
m = 3mm` # module d/z
αpressure=20degree` # pressure angle
z=12 # number of tooh
db=33.829mm` # diameter of base circle
rb=db/2 # radius of base circle
da,df=42mm`,28.5mm` # outside/root diameter
# require max involute angle determined by outside diameter
αupper=arccos(db/da)
θupper=tan(αupper)
f=λ θ:(λ α=arctan(θ):(rb/cos(α) cos(θ-α)-rb+`i rb/cos(α) sin(θ-α)))()
vInvlt=~[f(x) for x in klsp(0,θupper)]
invα=tan(αpressure)-αpressure
θtoothCenterAngle=2pi/(2z)+2invα
θtoothBaseRootAngle=2pi/(2z)-2invα
r,θ= 0.00215788829426498*m`, 2.27309298984rad`
vArc=((-~[r exp(`i x) for x in klsp(-θ/2,θ/2)])[::-1]+ r cos(θ/2)+`i r sin(θ/2)
)*exp( `i arcsin(r sin(θ/2)/rb))+ rb cos(θtoothCenterAngle)
vTooth=np.r_[rb+vInvlt,
(exp(`i θtoothCenterAngle) ( rb + vInvlt.d))[::-1],
exp(`i θtoothCenterAngle) vArc
]
plotTrajectory(map(λ x:(x.real,x.imag),
sum([list(exp(2pi `i k/(z)) vTooth) for k in range(z)], [])
)
)
plotTrajectory(map(λ x:(x.real,x.imag),
sum([list(d+ exp(2pi `i k/(z)) vTooth) for k in range(z)], [])
)
,color=red
)
//@@@
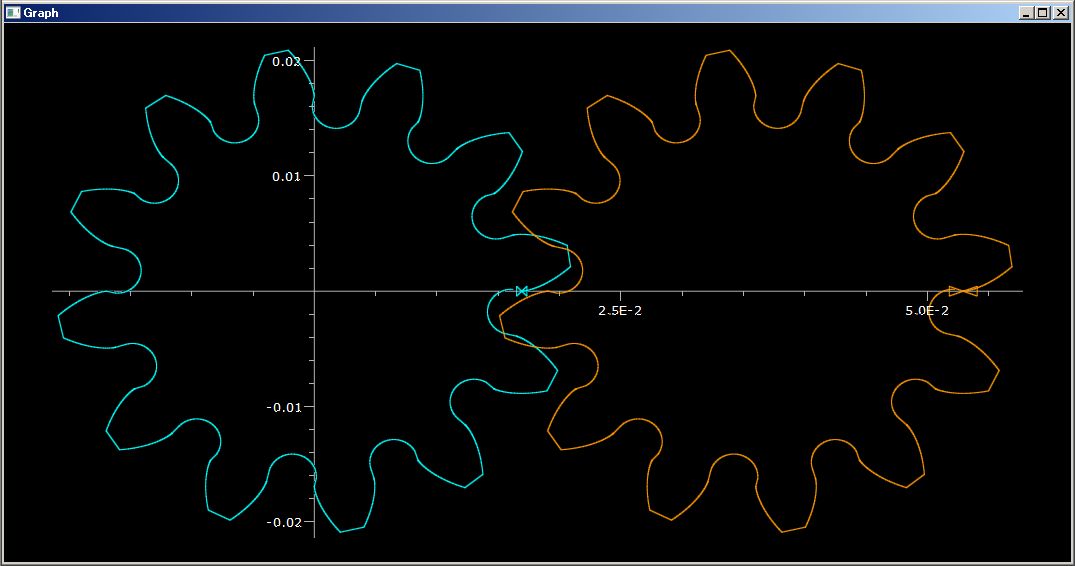
上のように二つの歯車を並べて描かせてみると、「歯みぞの幅」と「円弧歯厚」を同じにして正解のようです。歯数に関係なく、両者を同じサイズのとき歯車のバックラッシュがなくなりそうなことが、歯車の図より見えてきるからです。
その他にも実際に描かせるまでには、様々の資料の説明不足な点や理解不足な点の補足が必要でした。四日つぶれましたが良い勉強になりました。おかげで「歯車の中心距離がずれても歯のかみ合わせ部分での擦れは発生しない」「インボリュート曲線の配置は転移させられる」「インボリュート曲線を n 倍にしたものなど、別の曲線でも擦れが発生しない歯の形がある」などが分かりました。
この間プログラムのデバッグ作業自体は殆どありませんでした。工学・数学での検討が大部分でした。平歯車の詳しい動作について理解したい方は、上のコードを自分の対象とする問題での歯車に、置き換えてみると良い勉強になると思います。。
PythonSf には、ラプラス演算子 s に対応する有理関数クラスの単項式 `s が備わっています。`s は z 変換の単項式としても扱えます。。これを使えばアナログ・フィルタ、デジタル・フィルタの挙動が短い PythonSf ワン・ライナー式で簡単に計算できます。Matlab,Mathematica など他の数学ソフトでは、ここまで簡単には計算できないと思います。以下の one-liners を見てやってください。
標準配布の PythonSf に備わっている `s を使えば、回路の Laplace 演算子を使った式を扱えます。そのボード線図、インパルス応答、インディシャル応答が簡単に求められます。この `s を使って下の L C R を組み合わせた回路の動作を検討してみましょう。
L C R 回路
11mH 10Ω
Vi ──∩∩∩∩ ─WMWM─┐ ──→ Vo
│
─┴─
─┬─
│1uF
│
Ξ
コイル L は微分要素であり、その Lapalace 演算子表現は L `s です。C は積分要素であり、その Laplace 演算子表現は 1/(C `s) です。ですから L C R 三つを直列につないだときの impedence の Laplace 演算子表現 (L `s + 1/(C `s) + R) となります。
ですから、上の回路の電圧伝達関数 Vo/Vi は下のように PythonSf 式で計算できます。この伝達関数を何回か再利用するため、ファイル変数 G としてカレント・ディレクトリに残すことも、下の PythonSf 式の G:= ... の式で行わせています。
PythonSf ワンライナー
L,C,R=1000uH`, 1uF`, 10Ω`; G:=1/(C `s)/(L `s + 1/(C `s) + R)
===============================
1e+09
-------------------
2
s + 1e+04 s + 1e+09
この伝達関数 G が どんなものか Python に備わっている自己ドキュメント機能を使って調べてみましょう。
PythonSf ワンライナーたち
# G は どんなクラス? ----- ClRtnl クラス
=:G; type(G)
===============================
<class 'pysf.rational.ClRtnl'>
# ClRtnl はどんなメソッドを備えている?
np.info(ClRtnl)
ClRtnl(numerAg, denomAg=1, variable='s')
' Ratianal Function class
The highest coefficient of demoninator is always 1
'
Methods:
getAnRspns --
getDgRspns --
deriv -- Return the derivative of this rational funciton.
plotDgGnPh --
getAnImpls --
plotBode --
getRtnlOfRtnl --
getDgImpls --
plotAnRspns --
===============================
None
# G が保持しているデータは? ---- 分母と分子の多項式
=:G; vars(G)
===============================
{'m_plNumer': poly1d([ 1.00000000e+09]), 'm_plDenom': poly1d([ 1.00000000e+00, 1.00000000e+04, 1.00000000e+09])}
G は plotBode(..) 関数を備えています。この関数で Bode 線図を描きます。名前から Bode 線図を描かせる関数だと分かります。どんな使い方をするのでしょうか調べましょう。
PythonSf ワンライナー
# ClRtnl:plotBode 関数の使い方を調べる
=:G; np.info(G.plotBode)
plotBode(lowerFreq, higherFreq=None)
' plot Bode diagram using matplotlib
Default frequency width is 3 decades
'
===============================
None
Bode 線図を描かせるには周波数範囲を指定してやる必要があるようです。伝達関数 G は m_plDenon: poly1d 多項式のインスタンスを備えています。ならば、その根が判れば Bode 線図の周波数範囲も決まります。
PythonSf ワンライナー
=:G; G.m_plDenom.roots
===============================
[-5000.+31224.98999199j -5000.-31224.98999199j]
上の計算結果:分母多項式の根は 3kHz 周波数近辺に共振することを示しています。ならば その二桁下 10Hz から二桁上 100kHz の範囲の周波数でボード線図を描けば良さそうです。
PythonSf ワンライナー
=:G; G.plotBode(10Hz`, 100k` Hz`)
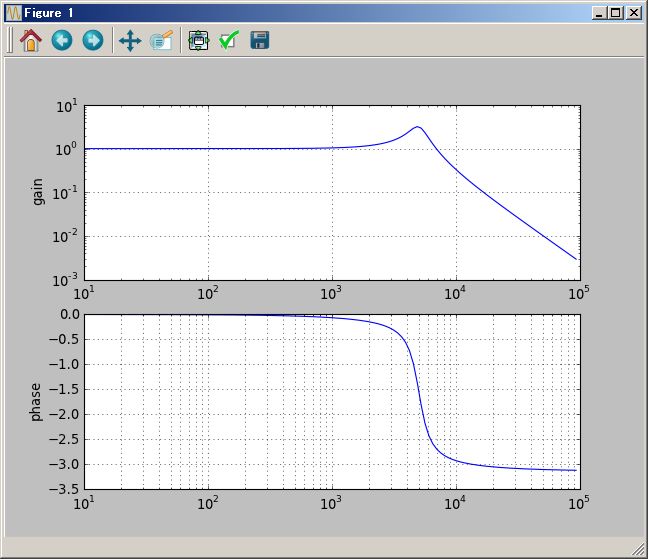
plotAnImpls(..) 関数を使って、上の回路のインパルス応答を見てみましょう。グラフの時間表示範囲は 3kHz より判断して、時間の範囲は 0 -- 2ms としましょう。
PythonSf ワンライナー
=:G; plotGr(G.getAnImpls( 2ms`))
PythonSf ワンライナー
=:G; G.()
インパルス応答の次は plotAnRspns(..) メソッドを使ってステップ応答を見てみましょう。
PythonSf ワンライナー
=:G; G.plotAnRspns( 2ms`)
今度は上の回路に 1kHz 正弦波を入力したときの応答をみてみましょう。 1kHz 正弦波関数は sin(2pi 1k` Hz` `T) と記述できます。(0,2ms) の区間を 256 等分したベクトル・データは klsp(0,2ms`,256) で作れます。これを引数にして sin(2pi 1k` Hz` `T)(klsp(0,2ms`,256) を計算してやれば、ikHz 正弦波の 2ms までの 256 点のベクトル・データが得られます。このデータを上の .getAnRspns(..) の二番目の引数に与えれやれば、上の回路に正弦波入力を与えたときの応答が得られます。
PythonSf ワンライナー
=:G;G.plotAnRspns(2ms`,sin(2pi 1k` Hz` `T)(klsp(0,2ms`, 256)))
コンデンサ 1uF に充電が完了するまでの時間:初期の 0.5ms までは L C 共振成分が見られますが、それ以後は 1kHz の正弦波になっています。
ちなみに、矩形波入力を入れたときは次のような応答波形になります
PythonSf ワンライナー
=:G;G.plotAnRspns(2ms`,[(λ t:-1-2np.floor(2 (-0.5+ t 1k` Hz` -int(t 1k` Hz`)) ))(x) for x in klsp(0,2ms`, 256)])
上の PythonSf 式で矩形波を作っている λ t:-1-2np.floor(2 (-0.5+ t 1k` Hz` -int(t 1k` Hz`)) ) が少しく技巧的です。こんなのは、すらすらとは出てこないでしょう。矩形波を表す関数を手続き的にプログラムするべきかもしれません。実際には下のような順序で導出しています。こっちは関数プログラミング的な導出方だと思います。こちらの方が数学的思考に集中できます。手続き的なプログラム作成に伴うデバッグが入らないからです。
PythonSf ワンライナーたち
plotGr(λ t: t-int(t 1k` Hz`), 0,10ms`)
plotGr(λ t: t 1k` Hz` -int(t 1k` Hz`), 0,10ms`)
plotGr(λ t: np.floor(2 (-0.5+ t 1k` Hz` -int(t 1k` Hz`)) ), 0,10ms`)
plotGr(λ t: np.floor(2 (-0.5+ t 1k` Hz` -int(t 1k` Hz`)) ), 0,2.5ms`)
plotGr([(λ t: np.floor(2 (-0.4+ t 1k` Hz` -int(t 1k` Hz`)) ))(x) for x in klsp(0,2ms`, 256)])
plotGr([(λ t: np.floor(2 (-0.5+ t 1k` Hz` -int(t 1k` Hz`)) ))(x) for x in klsp(0,2ms`, 256)])
plotGr([(λ t: 1+2np.floor(2 (-0.5+ t 1k` Hz` -int(t 1k` Hz`)) ))(x) for x in klsp(0,2ms`, 256)])
plotGr([(λ t:-1-2np.floor(2 (-0.5+ t 1k` Hz` -int(t 1k` Hz`)) ))(x) for x in klsp(0,2ms`, 256)])
RIAA 回路
R1:82kΩ R3:1kΩ
────WMWM───┬──────WMWM────┬────
│ │
≧ │
≦R2:12kΩ │
│ │
─┴─ ─┴─
─┬─ C1:0.027uF ─┬─ C2:8200pF
│ │
─────────┴────────────┴────
ここでは二端子網回路の F 行列を使って、上の RIAA 回路の電圧伝達関数を計算します。
標準配布 PythonSf の sfCrrntIni.py には、直列接続または並列接続の二端子網回路の F 行列を返す Fs(.) と Fp(.) が実装されています。これを使えば、上の RIAA 回路の R1 直列抵抗や R1 + 1/(C1 `s) 並列要素の F 行列は下のように計算できます。
PythonSf ワンライナーたち
R1=82kΩ`; Fs(R1)
===============================
[[ClRtnl([ 1.],[ 1.]), ClRtnl([ 0.],[1])],
[ClRtnl([-82000.],[ 1.]), ClRtnl([ 1.],[ 1.])]]
---- ClFldTns:< class 'pysf.rational.ClRtnl'> ----
R2,C1=12kΩ`,0.027uF`; Fp(R2+1/(C1 `s))
===============================
[[ClRtnl([ 1.],[ 1.]),
ClRtnl([ -8.33333333e-05, 0.00000000e+00],[ 1.00000000e+00, 3.08641975e+03])],
[ClRtnl([ 0.],[1]), ClRtnl([ 1.],[ 1.])]]
---- ClFldTns:< class 'pysf.rational.ClRtnl'> ----
RIAA 回路の要素ごとに F 行列が求められるのならば、それを掛け合わせてやれば RIAA 回路の F 行列が計算できます。下のような具合です。
PythonSf ワンライナー
R1,R2,R3,C1,C2=82kΩ`,12kΩ`,1kΩ`,0.027uF`,8200pF`; Fp(1/(C2 `s)) Fs(R3) Fp(R2+1/(C1 `s)) Fs(R1)
===============================
[[ ClRtnl([ 7.36633333e-04, 9.93395062e+00, 3.08641975e+03],[ 1.00000000e+00, 3.08641975e+03]),
ClRtnl([ -8.88333333e-09, -1.08641975e-04, 0.00000000e+00],[ 1.00000000e+00, 3.08641975e+03])],
[ ClRtnl([ -8.98333333e+04, -2.56172840e+08],[ 1.00000000e+00, 3.08641975e+03]),
ClRtnl([ 1.08333333e+00, 3.08641975e+03],[ 1.00000000e+00, 3.08641975e+03])]]
---- ClFldTns:< class 'pysf.rational.ClRtnl'> ----
F 行列が定まれば、その電圧伝達関数は -F[1,0] F[0,1]/F[0,0] + F[1,1] で計算できます。下のような具合です。
PythonSf ワンライナーたち
R1,R2,R3,C1,C2=82kΩ`,12kΩ`,1kΩ`,0.027uF`,8200pF`;F=Fp(1/(C2 `s)) Fs(R3) Fp(R2+1/(C1 `s)) Fs(R1);(-F[1,0] F[0,1]/F[0,0] + F[1,1])
===============================
3 2
1358 s + 1.257e+07 s + 3.88e+10 s + 3.991e+13
-------------------------------------------------------
4 3 2
s + 1.966e+04 s + 9.696e+07 s + 1.543e+11 s + 3.991e+13
R1,R2,R3,C1,C2=82kΩ`,12kΩ`,1kΩ`,0.027uF`,8200pF`;F=Fp(1/(C2 `s)) Fs(R3) Fp(R2+1/(C1 `s)) Fs(R1);(-F[1,0] F[0,1]/F[0,0] + F[1,1]).plotBode(1Hz`,100k` Hz`)
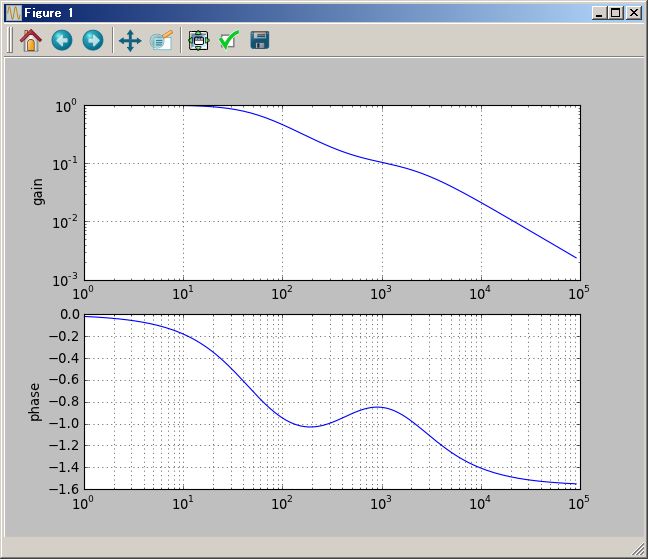
F 行列以外に Z 行列 Y 行列 などを返す関数を作ってやれば任意トポロジーの伝達関数を計算できるようになると思いますが、そこまでは実装していません。回路のプロのどなたか、この実装をしてみませんか。理屈さえわかっていれば、それらの実装は簡単です。Fs(.), Fp(.) 関数は下のような超が付くほどの簡単な実装で済んでいます。
PythonSf ワンライナー
np.source(Fs)
In file: sfCrrntIni.py
Fs = lambda Z:sf.krry__(*[[1.0,0.0],[-Z*1.0,1.0], sf.ClRtnl])
===============================
None
PythonSf ワンライナー
np.source(Fp)
In file: sfCrrntIni.py
Fp = lambda Z:sf.krry__(*[[1.0,-1.0/Z],[0.0,1.0], sf.ClRtnl])
===============================
None
`s を作っているクラス ClRtnl には、デジタル・フィルタ向けのインパルスも応答関数:getDgImpls(..)、ステップ応答・一般応答関数:getDgRspns(.;)、ゲイン・位相表示関数:plotDgGnPh(..) も備えています。ですから下のような z 変換を使った算計処理が可能です。
PythonSf ワンライナー
# FIR インパルス応答
z_=1/`s; (z_^1 + 2z_^2+ 3z_^3).getDgImpls()[:10]
===============================
[ 0. 1. 2. 3. 0. 0. 0. 0. 0. 0.]
---- ClTensor ----
PythonSf ワンライナー
# FIR ステップ応答
z_=1/`s; (z_^1 + 2z_^2+ 3z_^3).getDgRspns()[:10]
===============================
[ 0. 1. 3. 6. 6. 6. 6. 6. 6. 6.]
PythonSf ワンライナー
# IIR ステップ応答
z=`s; ((z +1)/(z^1 + 2z^2+ 3z^3)).getDgImpls()[:10]
===============================
[ 0. 0. 0.33333333 0.11111111 -0.18518519 0.08641975
0.00411523 -0.03155007 0.01966164 -0.00259107]
---- ClTensor ----
PythonSf ワンライナー
# IIR ゲイン・位相図の描画
z=`s; (z^-1 + 2z^-2+ 3z^-3).plotDgGnPh()
置換群 Sn(N) を実装しました。ただし群論に詳しくない素人の愚直な実装であり、計算時間を短くする対策が入っていません。N が 10 を超えた Sn(N) 置換群全体を iterate 処理させると計算に何時間もかかってしまいます。でも N が 8 ぐらいまでならば Sn(8) 全部を実用的に iterate することもできます。これぐらいまでの処理でも多くの有限群の性質を確認できます。これならば学部での群論の勉強には十分だと考えています。
標準配布の sfCrrntIni.py には置換群インスタンスのクラス:Sb、巡回置換インスタンスを返す関数 Cy、置換群インスタンスを要素とする frozenset クラス:kfs(..)、群生成関数:grp(..) をグローバル変数として定義し直してあるので、PythonSf 式で直接に使えます。 また標準配布のディレクトリには置換群の集合インスタンス SS2,SS3,SS4,SS5、交代群の集合インスタンス SA3,SA4 のファイル変数を置いてあります。 これぐらい用意されていれば初等的な群論の検討には不便ないでしょう。
数学ソフトに詳しい方は「GAP を使えよ」と仰ると思います。同意します。複雑な群論の処理、大規模な対象を扱うときは GAP を使うべきです。でも Sn(8) ぐらいまでの小規模な群までならば、Vim などから PythonSf 式で扱える Sb, Cy, ksf, grp のほうが便利です。以下の PythonSf 式による群の扱いを見てください。
以下有限置換群 Sn(N) を扱う Sb,Cy,group,kfs といったクラスや関数の詳細を見ていきます。
Sb(...) は 0 から n までの整数を並べ替えたシーケンスを引数に与えることで置換インスタンスを作ります。この並べ替えたシーケンス引数は、多変数引数として与えます。またリストあるいはタプル引数でも与えられます。
PythonSf ワンライナーたち
# 多変数引数
Sb(1,3,2,0)
===============================
Sb(1,3,2,0)
# リスト引数
x=[1,3,2,0]; Sb(x)
===============================
Sb(1,3,2,0)
# タプル引数
x=(1,3,2,0); Sb(x)
===============================
Sb(1,3,2,0)
Sb インスタンスどうしの掛け算と Sb インスタンスへの整数べき乗算が可能です。長さの異なる Sb インスタンスの積も可能です。下のような PythonSf 式として置換インスタンスの計算を扱えます。
PythonSf ワンライナーたち
# Sb インスタンスどうしの積
a,b=Sb(1,3,2,0), Sb(3,0,2,1); a b
===============================
Sb(0,1,2,3)
# Sb インスタンスの 2 乗
Sb(1,3,2,0)^2
===============================
Sb(3,0,2,1)
# Sb インスタンスの -1 乗:逆元
Sb(1,3,2,0)^-1
===============================
Sb(3,0,2,1)
# Sb インスタンスの 2 乗
Sb(1,3,2,0)^-2
===============================
Sb(1,3,2,0)
# Sb インスタンスの 3 乗:単位元に戻る
Sb(1,3,2,0)^3
===============================
Sb(0,1,2,3)
# 異なる長さの Sb インスタンスの積
Sb(1,3,2,0) Sb(1,3,2,0,4)
===============================
Sb(3,0,2,1,4)
# 異なる長さの Sb インスタンスの積 2
Sb(1,3,2,0) Sb(1,4,2,0,3)
===============================
Sb(3,4,2,1,0)
# 巡回群リストの生成
a=Sb(1,3,2,0); [a^k for k in range(4)]
===============================
[Sb(0,1,2,3), Sb(1,3,2,0), Sb(3,0,2,1), Sb(0,1,2,3)]
# 長い Sb インスタンス
seed(0);Sb(shuffle(range(20)))
===============================
Sb(16,9,19,10,2,11,15,13,4,7,0,18,1,17,5,8,3,6,12,14)
Cy(..) 関数は巡回置換 Sb(..) インスタンスを返します。Sb(..) のときとは違って、必要な整数の組み合わせだけを引数に与えれば済むので、置換群の PythonSf 式の記述が簡単になることが多くあります。
PythonSf ワンライナーたち
Cy(1,2,3)
===============================
Sb(0,2,3,1)
Cy(1,3)
===============================
Sb(0,3,2,1)
Cy(1,3) Sb(range(10))
===============================
Sb(0,3,2,1,4,5,6,7,8,9)
# a cyclic attribute
Sb(16,9,19,10,2,11,15,13,4,7,0,18,1,17,5,8,3,6,12,14).cyclic
===============================
Cy(0,16,3,10) Cy(1,9,7,13,17,6,15,8,4,2,19,14,5,11,18,12)
Cy(0,16,3,10) Cy(1,9,7,13,17,6,15,8,4,2,19,14,5,11,18,12)
===============================
Sb(16,9,19,10,2,11,15,13,4,7,0,18,1,17,5,8,3,6,12,14)
# an cyclic group and an multiplication of transpositions
(Cy(0,2) Cy(2,4) Cy(4,1) Cy(1,8)).cyclic
===============================
Cy(0,2,4,1,8)
# transpositions and Sn(N)
# Sn(4) == group([Cy(0,1),Cy(1,2),Cy(2,3)}
=:SS4; SS4 == group([Cy(0,1),Cy(1,2),Cy(2,3)])
===============================
True
Sb インスタンスを要素とする置換群の集合を扱うとき、その集合は frozenset の方が望ましいことが多くあります。関数で引き渡した先で変更されないことが保証されます。set のときのように copy/deep_copy に注意を払わなくて済むからです。そして置換要素の集合としての群は kfs:frozenset で扱うことに統一しておかないと、== 演算子での判断が面倒になってしまいます。
でも frozenset のスペルは PythonSf 式の one-liner 記述には長すぎます。そこで frozenset を継承した kfs クラスを設けました。ついでに kfs 集合の union(..) は + 演算子で可能にしました。kfs 集合の meet(..) は * 演算子で可能にしました。
ついでに frozenset を iterate するとき、その繰り返し順序が判らないと困ることが多いので sortedList:sl プロパティを設けて、sort 済みのリストを返すようにしました。これでデバッグが楽になります。ループ処理ごとに、どのインスタンスをを処理しているのかが判るからです。kfs(..) 集合をプリントするときも sorted 済みの結果で表示します。
PythonSf ワンライナーたち
# Sb インスタンスよりなる kfs 集合の生成
kfs([Sb(0,1), Sb(2,1,0)])
===============================
kfs([Sb(0,1), Sb(2,1,0)])
# 巡回群集合の生成
a=Sb(1,3,2,0); kfs( [a^k for k in range(4)] )
===============================
kfs([Sb(0,1,2,3), Sb(1,3,2,0), Sb(3,0,2,1)])
# 集合の和:union
a=Sb(1,3,2,0); b,c=kfs( [a^k for k in range(4)] ), kfs([Sb(0,1), Sb(2,1,0)]); b+c
===============================
kfs([Sb(0,1), Sb(2,1,0), Sb(0,1,2,3), Sb(1,3,2,0), Sb(3,0,2,1)])
# 集合の積:meet
a=Sb(1,3,2,0); b,c=kfs( [a^k for k in range(4)] ), kfs([Sb(0,1), Sb(3,0,2,1)]); b*c
===============================
kfs([Sb(3,0,2,1)])
ただし kfs クラスの要素にできるのは sort 可能なインスタンスに限られます。最後の結果をコンソールに質力するときに sort 作業がなされるからです。ですから整数・実数・複素要素値のベクトルや行列を要素とするkfs 集合は作れません。コンソールに出力するときの sorting でエラーになります。下のような具合です
PythonSf ワンライナー
kfs([~[1,2],~[3,4]])
===============================
The truth value of an array with more than one element is ambiguous. Use a.any() or a.all() at excecuting:kfs([krry__(*[1,2]),krry__(*[3,4])])
PythonSf ブロック実行
//@@
a=kfs([~[1,2],~[3,4]])
print a+5
//@@@
Traceback (most recent call last):
File "__tempConverted.py", line 9, in
print a+5
File "D:\my\vc7\mtCm\pysf\ptGrp.py", line 432, in __str__
return "kfs(" + str(self.sl) + ")"
File "D:\my\vc7\mtCm\pysf\ptGrp.py", line 357, in __getattr__
return sorted((self))
ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()
置換群の集合インスタンス SS2,SS3,SS4,SS5、交代群の集合インスタンス SA3,SA4 のファイル変数を、標準配布のカレント・ディレクトリに置いてあります。 これらは kfs クラスのインスタンスです。
PythonSf ワンライナーたち
=:SS3; SS3
===============================
kfs([Sb(0,1,2), Sb(0,2,1), Sb(1,0,2), Sb(1,2,0), Sb(2,0,1), Sb(2,1,0)])
=:SA3; SA3
===============================
kfs([Sb(0,1,2), Sb(1,2,0), Sb(2,0,1)])
群論の剰余類・共役類などを扱うのを容易にするため、kfs 集合インスタンスと 置換要素との積を可能にしています。同様な意味で kfs 集合インスタンスと要素との和も可能にしています。もちろん置換群の kfs 集合インスタンスと置換群要素の和演算は無意味でありエラーになります。でも整数集合などでは意味がある分野もあるでしょう。次のような PythonSf 式計算ができます。
PythonSf ワンライナーたち
# 置換集合と置換の積
a=Sb(1,3,2,0); SG=kfs( [a^k for k in range(4)] ); g=Sb(3,2,1,0); SG g
===============================
kfs([Sb(0,2,3,1), Sb(1,2,0,3), Sb(3,2,1,0)])
# 共役集合の計算 1
a=Sb(1,3,2,0); SG=kfs( [a^k for k in range(4)] ); g=Sb(3,2,1,0); g SG g^-1
===============================
kfs([Sb(0,1,2,3), Sb(2,1,3,0), Sb(3,1,0,2)])
# 共役集合の計算 2
a=Sb(1,3,2,0); SG=kfs( [a^k for k in range(4)] ); g=Sb(3,2,1,0); g^-1 SG g
===============================
kfs([Sb(0,1,2,3), Sb(2,1,3,0), Sb(3,1,0,2)])
# 整数集合と整数の積
kfs([1,2,3]) 4
===============================
kfs([4, 8, 12])
# 整数とタプルの集合と整数の積
kfs([1, (2,3)]) 4
===============================
kfs([4, (2, 3, 2, 3, 2, 3, 2, 3)])
# 整数集合と整数の積
kfs([1,2,3]) + 4
===============================
kfs([5, 6, 7])
一つだけ kfs 要素が Sb インスタンスであることを前提としているのが / 演算子です。ksf 集合を、その部分集合で割ることで左剰余類群の集合を返します。この機能は kfs 要素が Sb 以外であると旨く働きません。
PythonSf ワンライナー
=:SS3,SA3; SS3/SA3
===============================
kfs([Sb(0,1,2), Sb(0,2,1)])
group(..) 関数の引数に Sb インスタンスのリスト or タプル or セットを与えると、その Sb インスタンスたちによって生成される群の kfs 集合を返します。下のような PythonSf 式が使えます。
PythonSf ワンライナーたち
# group({ Sb(1,0), Cy(range(N)}) による Sn(N) 置換群全体集合の生成
N=3; group({Sb(1,0),Cy(range(N))})
===============================
kfs([Sb(0,1,2), Sb(0,2,1), Sb(1,0,2), Sb(1,2,0), Sb(2,0,1), Sb(2,1,0)])
# group({ Sb(1,0), Cy(range(4)}) による置換群全体集合が Sn(4) であることの確認
=:SS4; N=4; group({Sb(1,0),Cy(range(N))}) == SS4
===============================
True
group(..) 関数は、全ての積の組み合わせで作られる集合を作ります。それにより集合の新たな要素が追加されなくなるまでリカーシブに新たに集合を作り直します。ですから Sn(N):N が 10 以上の長い Sb インスタンスを group(..) に渡してやると、それ返す集合要素数は n! となるかも知れません。そうなると一時間でも計算が終わらなくなるでしょう。ご注意ください。
下の Cy と Sb を使った group を表す PythonSf 式は、D4 二面体群に対応しています。
PythonSf ワンライナー
`print(group({Cy(0,1,2,3), Sb(3,2,1,0)}).sl)
[Sb(0,1,2,3),
Sb(0,3,2,1),
Sb(1,0,3,2),
Sb(1,2,3,0),
Sb(2,1,0,3),
Sb(2,3,0,1),
Sb(3,0,1,2),
Sb(3,2,1,0)]
===============================
None
この D4 有限体群は、下の四角形の合同変換群に対応します。
1 0 (-1,1) (1,1)
┌──┐ ┌──┐
│ │ │ │
│ │ │ │
└──┘ └──┘
2 3 (-1,-1) (1,-1)
Sb(0,1,2,3) A : なにもしない
Sb(3,0,1,2) B : 原点を中心に90度左回転
Sb(2,3,0,1) C : 原点を中心に180左度回転
Sb(1,2,3,0) D : 原点を中心に270左度回転
Sb(3,2,1,0) E : x軸に関して折り返す
Sb(1,0,3,2) F : y軸に関して折り返す
Sb(0,3,2,1) G : 直線y=xに関して折り返す
Sb(2,1,0,3) H : 直線y=-xに関して折り返す
D5 五角形の合同変換群は下の PythonSf 式で書けます。
PythonSf ワンライナー
`print(group({Cy(0,1,2,3,4), Sb(4,3,2,1,0)}).sl)
[Sb(0,1,2,3,4),
Sb(0,4,3,2,1),
Sb(1,0,4,3,2),
Sb(1,2,3,4,0),
Sb(2,1,0,4,3),
Sb(2,3,4,0,1),
Sb(3,2,1,0,4),
Sb(3,4,0,1,2),
Sb(4,0,1,2,3),
Sb(4,3,2,1,0)]
===============================
None
一般の Dn を表す PythonSf 式が下のように書ける事も類推できると思います。
PythonSf ワンライナー
N=6;ls=range(N); `print(group({Cy(*ls),Sb(*(ls[::-1]))}).sl)
[Sb(0,1,2,3,4,5),
Sb(0,5,4,3,2,1),
Sb(1,0,5,4,3,2),
Sb(1,2,3,4,5,0),
Sb(2,1,0,5,4,3),
Sb(2,3,4,5,0,1),
Sb(3,2,1,0,5,4),
Sb(3,4,5,0,1,2),
Sb(4,3,2,1,0,5),
Sb(4,5,0,1,2,3),
Sb(5,0,1,2,3,4),
Sb(5,4,3,2,1,0)]
===============================
None
PythonSf 有限群論の最後に交換子群を実際に計算してみます。
群 G の交換子群は、下の集合を含む最小の群です。
{ x y x^-1 y^-1 for x,y ∈ G}
上の集合は交換子の集合であり、これだけでは群になる・演算が閉じている保障がありません。
でも群の交換子の集合で、群でない例は簡単には作れません。位数 96 の位置に、群にならない交換子の集合があるそうです。Sn(10) 以下の群を扱っている分には、上の交換子の集合は群だと思っていいでしょう。Sn(10) 以下で、そんな群を見つけられたら大発見です。交換子群は G に含まれる最大の正規部分群であり、色々と便利に使えます。
PythonSf ワンライナーたち
# Sn(3) の交換子積の集合
SS=:SS3; {x y x^-1 y^-1 for x,y in mitr(SS,SS)}
===============================
set([Sb(0,1,2), Sb(1,2,0), Sb(2,0,1)])
# Sn(3) の交換子群:交換子積の集合と同じ
SS=:SS3; group([x y x^-1 y^-1 for x,y in mitr(SS,SS)])
===============================
kfs([Sb(0,1,2), Sb(1,2,0), Sb(2,0,1)])
# Sn(4) の交換子積の集合
SS=:SS4; kfs([x y x^-1 y^-1 for x,y in mitr(SS,SS)])
===============================
kfs([Sb(0,1,2,3), Sb(0,2,3,1), Sb(0,3,1,2), Sb(1,0,3,2), Sb(1,2,0,3), Sb(1,3,2,0), Sb(2,0,1,3), Sb(2,1,3,0), Sb(2,3,0,1), Sb(3,0,2,1), Sb(3,1,0,2), Sb(3,2,1,0)])
# Sn(4) の交換子群:交換子積の集合と同じ
SS=:SS4; group([x y x^-1 y^-1 for x,y in mitr(SS,SS)])
===============================
kfs([Sb(0,1,2,3), Sb(0,2,3,1), Sb(0,3,1,2), Sb(1,0,3,2), Sb(1,2,0,3), Sb(1,3,2,0), Sb(2,0,1,3), Sb(2,1,3,0), Sb(2,3,0,1), Sb(3,0,2,1), Sb(3,1,0,2), Sb(3,2,1,0)])
SS=:SS4; Cm=kfs([x y x^-1 y^-1 for x,y in mitr(SS,SS)]); Cm == group(Cm)
===============================
True
# Sn(4) の交換子群は交代群:An(4) になる
SS=:SS4; =:SA4; group([x y x^-1 y^-1 for x,y in mitr(SS,SS)]) == SA4
===============================
True
# An(4) の交換子群
SS =:SA4; group([x y x^-1 y^-1 for x,y in mitr(SS,SS)])
===============================
kfs([Sb(0,1,2,3), Sb(1,0,3,2), Sb(2,3,0,1), Sb(3,2,1,0)])
PythonSf を使うということは、Ramanujan 級の計算能力を得られたということです。この能力を使えば様々の分野で数学を使った遊びが可能になります。以下、その遊びの幾つかを見ていきましょう。
元の Maxima の式
plot3d((1/8)*(6*exp(-(((2/3)*abs(x) - 1)^2 + ((2/3)*y)^2) - (1/3)*((2/3)*y + (1/2))^3) + (2/3)*exp(-%e^11*( (abs((2/3)*x) - 1)^2 + ((2/3)*y)^2)^2) + (2/3)*y - ((2/3)*x)^4),
http://www.rainbowseeker.jp/xoops/modules/newbb/viewtopic.php?topic_id=369&forum=10&noreadjump=1
PythonSf ワンライナー
x,y,e=`X,`Y,exp(1); plot3dGr((1/8)*(6*exp(-(((2/3)*absF(x) - 1)^2 + ((2/3)*y)^2) - (1/3)*((2/3)*y + (1/2))^3) + (2/3)*exp(-e^11*( (absF((2/3)*x) - 1)^2 + ((2/3)*y)^2)^2) + (2/3)*y - ((2/3)*x)^4),klsp(-3,3,100))
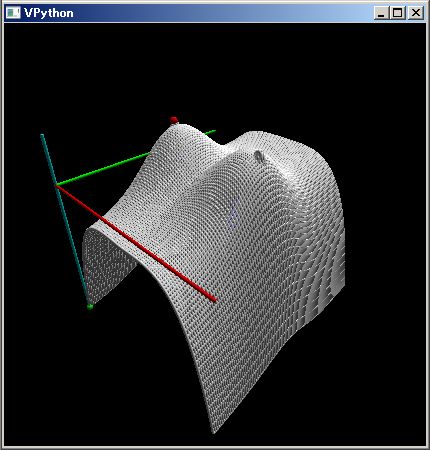
絶対値関数は Python に備わっている abs(..) 関数ではなく、PythonSf が用意している加減乗除べき乗算と関数合成が可能な absF(..) 関数を使います。 abs(..) 関数は python 文法に組み込まれており、これを呼び出すと引数オブジェクトの __abs__(self) method が呼び出されるからです。
なお左乳首が赤いのは意識してプログラムしたわけではありません。plot3dGr(..) は最初に出てくる最大値の位置に赤い丸を、最小値の位置に緑の丸を追加するため、左乳首の位置に赤い丸が置かれてしまいました。
フェルマーの最終定理:「n>=3 のとき x^n+y^n=z^n を満たす 0 でない自然数の組み合わせは存在しない」という定理は有名です。近年この問題は肯定的に証明されたようですが、素人に解る証明ではないでしょう。
単純な別証明なんて作れませんが、x^n + y^n よりは小さいが できるだけ近い z^n は存在するはずです。その z^n と x^n+y^n の差分がどんな分布をしているのか見てみましょう。n=3 のとき その分布は下の PythonSf ワン・ライナー式で計算できます。
PythonSf ワンライナー
N,n=16 ,3; ls=range(N); krry([ [(x^n+y^n)-((x^n+y^n+10^-9)^(1/n)//1)^n for x in ls] for y in ls], int)
===============================
[[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
[ 0 1 8 8 8 8 8 8 8 8 8 8 8 8 8 8]
[ 0 1 8 27 27 27 27 27 27 27 27 27 27 27 27 27]
[ 0 1 8 27 3 64 64 64 64 64 64 64 64 64 64 64]
[ 0 1 8 27 64 34 125 125 125 125 125 125 125 125 125 125]
[ 0 1 8 27 64 125 89 47 216 216 216 216 216 216 216 216]
[ 0 1 8 27 64 125 47 174 126 72 12 343 343 343 343 343]
[ 0 1 8 27 64 125 216 126 24 241 181 115 43 512 512 512]
[ 0 1 8 27 64 125 216 72 241 127 1 332 260 182 98 8]
[ 0 1 8 27 64 125 216 12 181 1 272 134 531 453 369 279]
[ 0 1 8 27 64 125 216 343 115 332 134 465 315 153 700 610]
[ 0 1 8 27 64 125 216 343 43 260 531 315 81 550 376 190]
[ 0 1 8 27 64 125 216 343 512 182 453 153 550 298 28 659]
[ 0 1 8 27 64 125 216 343 512 98 369 700 376 28 575 287]
[ 0 1 8 27 64 125 216 343 512 8 279 610 190 659 287 918]]
---- ClTensor ----
上の値分布は規則性を感じます。でも その規則を明晰には述べられません。N を 50 にまで広げて、その分布を三次元グラフとして表示してみましょう。
上の行列数値で感じたものに近い規則性があると思います。皆様は如何でしょうか。
PythonSf ワンライナー
N,n=50,3; ls=range(N); renderMtrx(krry([ [(x^n+y^n)-((x^n+y^n+10^-9)^(1/n)//1)^n for x in ls] for y in ls], int))
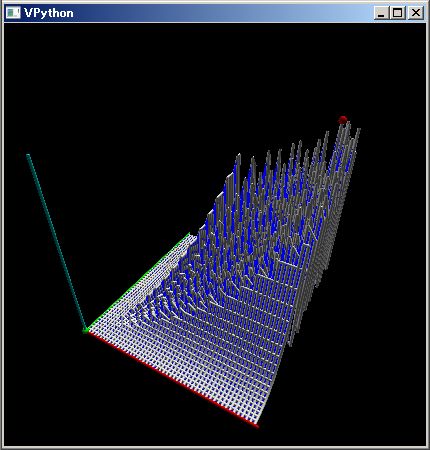
[0,1] 区間上のランダム値を返す rand(..) 関数, 平均値 0 分散 1 の正規分布ランダム値を返す randn(..) 関数、指定された範囲の整数値を返す randint(..) は、行列データも返せるので、手軽に様々な数値実験が可能です。その幾つかを示してみます。直感とは異なることも幾つかあるでしょう。ぜひとも、御自分の手で、様々の別パラメータ値で再実験をしてみてください。
1000 点の正規分布ノイズによる一次元の酔歩:Random Walk を下のように可視化できます。
PythonSf ワンライナー
#一次元の酔歩
N=1000; seed(0); lst=[0]; for v in randn(N):lst.append(lst[-1]+v); plotGr(lst)
上の図は株価変動に似ています。でもランダムなノイズによる Random Walk なのに変化に傾向性があるのが気になります。上の図を株価のグラフとして見せられたら、値下がりのトレンドにあると見なしてしまいます。
Numpy の random 関数に誤りがありトレンドが出やすくなっているのでしょうか。それとも本当にランダムであっても上のグラフ程度のトレンドは簡単に現れるものなのでしょうか。
分からんときに何かを変えてやると別の視点から見れることが多くあります。1000 点の一様ノイズによる一次元の酔歩:Random Walk を見てみましょう
PythonSf ワンライナー
N=1000; seed(0); lst=[0]; for v in rand(N)-0.5:lst.append(lst[-1]+v); plotGr(lst)
より変動が激しくなりました。これでもトレンドが伺えます。
もっと自然なランダム・データを使って、トレンドが出てくるかみれば、上のトレンドのようなものがランダムなデータにも出てくるか見えてくるはずです。円周率 1000 桁をランダムなデータとして Random Walk を描かせて見ましょう。
PythonSf ブロック
//@@
strData=(
"31415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679"
+"8214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196"
+"4428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273"
+"7245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094"
+"3305727036575959195309218611738193261179310511854807446237996274956735188575272489122793818301194912"
+"9833673362440656643086021394946395224737190702179860943702770539217176293176752384674818467669405132"
+"0005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235"
+"4201995611212902196086403441815981362977477130996051870721134999999837297804995105973173281609631859"
+"5024459455346908302642522308253344685035261931188171010003137838752886587533208381420617177669147303"
+"5982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989"
)
lst=[0]
#;; 4.5 == sum(range(10))/10
for ch in strData:lst.append(lst[-1]+int(ch)-4.5); plotGr(lst)
//@@@
円周率にランダムではないなんらかの傾向性があれば誰かが発表しているはずですが、そんな話は見られません。上の 1000 点の円周率のデータは、自然なランダム・データだと思ってよいでしょう。
この円周率データによる一次元の酔歩:Random Walk でもトレンドのようなものが見られます。どうも株価でトレンドといっているものにはランダムであることに起因する偶然なものも多くありそうです。
皆様も seed(.) の引数値を変えるなどしてランダム・データによるトレンドの具合の変化を、自分で体験してみてください。
二次元、三次元の酔歩も plotTrajectory(..) 関数を使えば容易に描けます。下のような具合です。
PythonSf ワンライナー
# 二次元の酔歩
N=1000; seed(0); lst=[~[0,0]]; for vc in randn(N,2):lst.append(lst[-1]+vc); plotTrajectory(lst)
PythonSf ワンライナー
# 三次元の酔歩
N=1000; seed(0); lst=[~[0,0,0]]; for vc in randn(N,3):lst.append(lst[-1]+vc); plotTrajectory(lst)
こんな図を見ていると、昔顕微鏡下の花粉の動きを生物としての動きと誤解したのも納得できます。
民生用の電子機器で使っている抵抗の大多数が、 3σ で 5% の精度のものです。1kΩ の抵抗を 10 個持ってきたら、その抵抗値のばらつきは正規分布に従うはずであり、以下のような具合になるはずです。
PythonSf ワンライナー
N=10; r,R=0.05, 1kΩ`; seed(0); R (1+ r/3 randn(N))
===============================
[ 1029.40087243 1006.66928681 1016.31229974 1037.34821999 1031.1259665
983.71203534 1015.83480696 997.47737986 998.2796858 1006.84330837]
---- ClTensor ----
ちなみに 5% 以上の誤差になるものは、1000 個の抵抗のうちで 2 個ぐらいです。
PythonSf ワンライナー
N=1000; r,R=0.05, 1kΩ`; vc=R (1+ r/3 randn(N)); len([ x for x in vc if x<0.95R or 1.05R<x])
===============================
2
10% 以上の誤差になるものは1000000 個の抵抗持ってきても 0 個です。
PythonSf ワンライナー
N=1000000; r,R=0.05, 1kΩ`; vc=R (1+ r/3 randn(N)); len([ x for x in vc if x<0.9 R or 1.1 R<x])
===============================
0
以上の計算より、5% 3σ 精度の抵抗値は、500 個に一個程度 5% を超えるものがある。でも 100 万個の抵抗をもってきても 10% を超える誤差のものは出てこないといえます。
ちなみに、5% 抵抗を合成してやると、抵抗の誤差同士が打ち消しあって より少ない抵抗値のばらつきになります。
下の回路の合成抵抗値は並列接続で半分になり直接接続で倍になるので、全体としては 1kΩ に戻ります。
1kΩ 1kΩ
┌─WMWM─┐ ┌─WMWM─┐
──┤ ├───┤ ├─
│ 1kΩ │ │ 1kΩ │
└─MWMW─┘ └─MWMW─┘
この回路の抵抗値 1kΩ のばらつき具合:標準偏差は下のようにシミュレーション計算できます。
PythonSf ワンライナー
N=1000; r,R=0.05, 1kΩ`; seed(0); vc=[ (vc1~+vc2)+(vc3~+vc4) for vc1,vc2,vc3,vc4 in R (1+ r/3 randn(N,4))]; sqrt( sum([ (x-sum(vc)/N)^2 for x in vc ])/(N-1) )
===============================
8.31846294487
元の標準偏差 1kΩ, 5%, 3σ から定まる抵抗値のばらつきぐあい 50/3 の半分程度のばらつきぐあいになりました。
「四次元立方体を三次元に射影する」ことを PythonSf で行います。でも最初からでは難しいので「三次元立方体を二次元に射影する」ことを行ってから、それを四次元に拡張する手順を踏みます。
PythonSf での one-liners を使って思考の螺旋階段を上っていく様子がよく分かる例だと思います。
三次元立方体の頂点は下の PythonSf 式で表現できます。
PythonSf ワンライナー
# 三次元立方体の頂点
ls=[-1,1]; [ ~[x,y,z] for x,y,z in mitr(ls,ls,ls)]
===============================
[ClTensor([-1., -1., -1.]), ClTensor([-1., -1., 1.]), ClTensor([-1., 1., -1.]), ClTensor([-1., 1., 1.]), ClTensor([ 1., -1., -1.]), ClTensor([ 1., -1., 1.]), ClTensor([ 1., 1., -1.]), ClTensor([ 1., 1., 1.])]
下の one-liner の方が、八個の頂点が分かりやすいですね。
PythonSf ワンライナー
# 2^3:八個の頂点
ls=[-1,1]; ~[ [x,y,z] for x,y,z in mitr(ls,ls,ls)]
===============================
[[-1. -1. -1.]
[-1. -1. 1.]
[-1. 1. -1.]
[-1. 1. 1.]
[ 1. -1. -1.]
[ 1. -1. 1.]
[ 1. 1. -1.]
[ 1. 1. 1.]]
---- ClTensor ----
座標軸の原点一箇所から放出される光線が立方体の各頂点を通って平面と交わる点を求めることで、立方体を平面に射影できます。そのため Z 軸に垂直な射影される平面を想定します。その Z 軸との交点は 12 の位置にあるものとしましょう。
原点一箇所から放出される光線が、上で作った立方体の八個の頂点を通って平面に射影されるよう、 その立方体をZ 軸方向に 6 だけ平行移動させます。下の PythonSf 式を使って、カレント・ディレクトリの mt.pvl ファイルに、その頂点の座標値を残します。 。
PythonSf ワンライナー
ls=[-1,1]; mt:= ~[ ~[x,y,z] for x,y,z in mitr(ls,ls,ls)]+ ~[0,0,6]
===============================
[[-1. -1. 5.]
[-1. -1. 7.]
[-1. 1. 5.]
[-1. 1. 7.]
[ 1. -1. 5.]
[ 1. -1. 7.]
[ 1. 1. 5.]
[ 1. 1. 7.]]
---- ClTensor ----
[0,0,0] 原点から放射された光線が、上で求めた八つの頂点を通って、上で想定した Z 軸に垂直な平面で交わったと想定し、その平面と直線の交点座標を求めましょう。
「Z 軸に直行し [0,0,12] で交わる平面」と「原点と ~[x,y,z] 点を通った直線」が交わる点の座標を求めます。
(t ~[x,y,z])[2] == 12 for ∃t
t z == 12
∴
t = 12/z for z ∈ {5,7}
ゆえに平面との交点の座標は下の PythonSf 式で計算できる
12/z ~[x,y,z]
具体例で再度考えましょう。「Z 軸に直行し [0,0,12] で交わる平面」と「原点と ~[-1,-1,7] 点を通った直線」が交わる点の座標は次の PythonSf 式で求められます。
PythonSf ワンライナー
12/7 ~[-1,-1,17]
===============================
[ -1.71428571 -1.71428571 29.14285714]
---- ClTensor ----
ですから、上で作った立方体の八つの頂点を通る、座標軸の原点から射出されて光線は下の八つの点で平面と交わります。この点は mt2dCube の名前のファイル変数で保存します。
PythonSf ワンライナー
=:mt; mt2dCube:=~[ v 12/v[2] for v in mt]
===============================
[[ -2.4 -2.4 12. ]
[ -1.71428571 -1.71428571 12. ]
[ -2.4 2.4 12. ]
[ -1.71428571 1.71428571 12. ]
[ 2.4 -2.4 12. ]
[ 1.71428571 -1.71428571 12. ]
[ 2.4 2.4 12. ]
[ 1.71428571 1.71428571 12. ]]
---- ClTensor ----
ファイル変数 mt, mt2dCube それぞれ八つの座標位置を人間に分かりやすいように、下の PytthonSf 式を使って図示します。
PythonSf ワンライナー
mt,mt2=:mt,mt2dCube; for v0,v1 in combinate(mt,2):plotTrajectory([v0,v1]); for v0,v1 in combinate(mt2,2):plotTrajectory([v0,v1],color=red);
上の図で赤い部分が立方体の射影図です。
三次元の立方体を平面に射影することと殆ど同様に、四次元立方体を四次元の超平面:三次元空間に射影できます。
四次元立方体の 2^4:16 個の頂点を、第4の 軸方向に 6 だけ平行移動させたときの頂点の座標をファイル変数 mt に残します。
PythonSf ワンライナー
ls=[-1,1]; mt:= ~[ ~[x,y,z,t] for x,y,z,t in mitr(ls,ls,ls,ls)]+ ~[0,0,0,6]
===============================
[[-1. -1. -1. 5.]
[-1. -1. -1. 7.]
[-1. -1. 1. 5.]
[-1. -1. 1. 7.]
[-1. 1. -1. 5.]
[-1. 1. -1. 7.]
[-1. 1. 1. 5.]
[-1. 1. 1. 7.]
[ 1. -1. -1. 5.]
[ 1. -1. -1. 7.]
[ 1. -1. 1. 5.]
[ 1. -1. 1. 7.]
[ 1. 1. -1. 5.]
[ 1. 1. -1. 7.]
[ 1. 1. 1. 5.]
[ 1. 1. 1. 7.]]
---- ClTensor ----
第四の軸に直行し [0,0,0,12] で交わる超平面に、原点と立方体の頂点を通る直線が交わる座標を求め、ファイル変数 mt3dCube に残します。
PythonSf ワンライナー
=:mt; mt3dCube:=~[ v 12/v[3] for v in mt]
===============================
[[ -2.4 -2.4 -2.4 12. ]
[ -1.71428571 -1.71428571 -1.71428571 12. ]
[ -2.4 -2.4 2.4 12. ]
[ -1.71428571 -1.71428571 1.71428571 12. ]
[ -2.4 2.4 -2.4 12. ]
[ -1.71428571 1.71428571 -1.71428571 12. ]
[ -2.4 2.4 2.4 12. ]
[ -1.71428571 1.71428571 1.71428571 12. ]
[ 2.4 -2.4 -2.4 12. ]
[ 1.71428571 -1.71428571 -1.71428571 12. ]
[ 2.4 -2.4 2.4 12. ]
[ 1.71428571 -1.71428571 1.71428571 12. ]
[ 2.4 2.4 -2.4 12. ]
[ 1.71428571 1.71428571 -1.71428571 12. ]
[ 2.4 2.4 2.4 12. ]
[ 1.71428571 1.71428571 1.71428571 12. ]]
---- ClTensor ----
四次元での超平面:すなわち三次元空間に射影された四次元立方体の三次元図を下の PythonSf 式で描きます。
PythonSf ワンライナー
mt=:mt3dCube; [plotTrajectory([v0[:3],v1[:3]])for v0,v1 in combinate(mt,2) if norm(v0-v1)~==4.8 or norm(v0-v1)~==(2*1.71428571)]
五次元立方体を四次元超平面に射影し、その四次元立体をさらに三次元空間に射影したときの頂点の位置も次の PythonSf 式で描けます。
PythonSf ワンライナー
ls=[-1,1]; mt= ~[ v for v in mitr(*[ls]*5)]+ ~[0,0,0,0,6];mt=~[ v 12/v[4] for v in mt][:,:-1]+[0,0,0,6]; mt=~[ v 12/v[3] for v in mt][:,:-1];plotPt(mt); drawAxis()
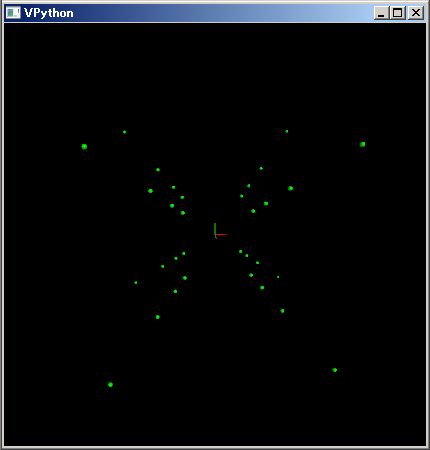
こんな図形は自分の手で回転させ様々の方向から見てみないと分かりにくいと思います。ぜひ上の one-liner で御自分のコンピュータで動かしマウスで動かしてみてください。
ここで行った立方体を平面に、四次元立方体を三次元に射影する PythonSf 式たちは、プログラム・コードを書いているのではなく、数式を書き連ねていると言ったほうが近いと思います。プログラム・コード記述の苦しさが殆どありません。面倒なプログラム・デバッグもありません。数学思考に集中できます。途中までの計算結果を見ながら PythonSf 式を書き連らねているだけです。
ハノイの塔の動作を記述するプログラムを下の PythonSf ワン・ライナーで記述できます。ただし、一回の関数呼び出しで三重の再起呼び出しを行わねばならないので、すこしく分かりにくいコードになります。
PythonSf ワンライナー
hanoi=λ n,f,t,v: None if n==1 else `print(str(n)+':'+f+'->'+t) or hanoi(n-1,f,v,t) or `print('move lefted one:'+f+'->'+t) or hanoi(1,f,t,v) or `print('take back '+str(n-1)+':'+v+'->'+t) or hanoi(n-1,v,t,f); hanoi(4,'a','b','via')
ここにある Python コードの直ぐ下にある R コードに近いコードになっています。Python コードより解り易いと思います。コードを修正してテスト実行を繰り返すにはワン・ライナーのほうが便利ですが、ブロックであらわしたほうが可読性が高くなります。
PythonSf ブロック
//@@
hanoi=λ n,f,t,v:\
None if n==1\
else \
`print(str(n)+':'+f+'->'+t)\
or hanoi(n-1,f,v,t)\
or `print('move lefted one:'+f+'->'+t)\
or hanoi(1,f,t,v)\
or `print('take back '+str(n-1)+':'+v+'->'+t)\
or hanoi(n-1,v,t,f)
hanoi(4,'a','b','via')
//@@@
'4:a->b'
'3:a->via'
'2:a->b'
'move lefted one:a->b'
'take back 1:via->b'
'move lefted one:a->via'
'take back 2:b->via'
'2:b->via'
'move lefted one:b->via'
'take back 1:a->via'
'move lefted one:a->b'
'take back 3:via->b'
'3:via->b'
'2:via->a'
'move lefted one:via->a'
'take back 1:b->a'
'move lefted one:via->b'
'take back 2:a->b'
'2:a->b'
'move lefted one:a->b'
'take back 1:via->b'
とブロック・コードにしても三重の再起は解り難いものです。要は 4 枚のディスクを a から b に移動させるときは、上側の三枚を via に移動可能なことにしてしまい、残りの一枚を a から b に移動させるということです。「上側の三枚を via に移動可能なことにした。」のを再起呼び出しで実行すると言うことです。この様子を下に図示してみました。参考にしてください。
┌─────────────────────────────┐
↑ ↓
'4:a->b'
│ │ │
─ │─ │ │
── │── -----+ │ │
─── │─── | │ │
──── │──── | │ │
─┴─ | ─┴─ ─┴─
a | via b
'3:a->via'
│ | │ │
│ | │ │
│ | ─ │─ │
│ +----→ ── │── │
──── │──── -----+ ─── │─── │
─┴─ | ─┴─ ─┴─
a | via b
+-----------------------------------+
│ │ | │
│ │ 'move lefted one:a->b' │
│ ─ │─ | │
│ +------- ── │── --------+ ↓ │
│ | ─── │─── | ──── │────
─┴─ | ─┴─ | ─┴─
a | via | b
'2:via->a' '3:via->b'
| |
| |
│ | │ | │
│ | │ | │
│ | │ | │
─ │─ ←-------+ │ | │
── │── ─── │─── | ──── │────
─┴─ ─┴─ | | ─┴─
a via | | b
'move lefted one:via->b'|
│ │ | | │
│ │ | | │
│ │ | | │
─ │─ │ +-------------→ ─── │───
── │── ----------+ │ | ──── │────
─┴─ | ─┴─ | ─┴─
a '2:a->b' via | b
| |
+-------------------------→|
|
│ │ | │
│ │ | │
│ │ | │
│ │ | ─── │───
── │── ─ │─ | ──── │────
─┴─ ─┴─ | ─┴─
a via | b
|
|
│ │ | │
│ │ | ─ │─
│ │ +------→ ── │──
│ │ ─── │───
│ │ ──── │────
─┴─ ─┴─ ─┴─
a via b
Python の正規表現は使いにくすぎます。Perl でのような正規表現を使いまくるコードを書く気にはなれません。正規表現をコンパイルしてから チェックする文字列に match(...) させ group(..) で取り出すなんて面倒なことをしてられません。そこで kre.py 正規表現改良モジュールを作りました。正規表現にマッチング・インスタンスを「対象文字列 / 正規表現」と割り算演算子で返すようにしました。部分文字列を「%(序数)」mod 演算子で返すようにしました。「対象文字列 / 正規表現%0」で正規表現にマッチした文字列を返すようにしました。
PythonSf では krgl('正規表現文字列') でコンパイル済みの正規表現インスタンスを作ります。これで対象文字列を割ってやれば、正規表現処理されたマッチング・インスタンスができます。これを %0 でわれば、マッチする文字列が帰ります。次のような具合です。
PythonSf ワンライナーたち
'abcdefg'/krgl('[c-e]*')%0
===============================
cde
'abcdefghijkl'/krgl('([c-e]*).*([g-i]+)')%0
===============================
abcdefghi
'abcdefghijkl'/krgl('([c-e]+).*([g-i]+)')%1
===============================
cde
'abcdefghijkl'/krgl('([c-e]*).*([g-i]+)')%2
===============================
i
PythonSf 正規表現クラス krgl を使えばワンライナーで実用的なことが様々にできます。次のような具合です。
PythonSf ワンライナーたち
# pysf ディレクリとにあるファイルのうち k で始まるファイル名のものを列挙します
rg,wlk=krgl('^k'),os.walk('./pysf'); `print( [(path,[f for f in files if f/rg%0]) for path,dir,files in wlk] )
[('./pysf',
['kcommon.py',
'kcommon.pyc',
'kmayavi.py',
'kmayavi.pyc',
'kmayaviPy.bak',
'kNumeric.bak',
'kNumeric.py',
'kNumeric.pyc',
'kNumericPy.bak',
'kre.py',
'kre.pyc'])]
===============================
None
# PythonSf の実行時に定まっているグローバル変数の中から plot で始まるものを列挙する
# PythonSf のグローバル変数で不正確に記憶している名称を探すのに便利です
rg=krgl('^plot'); [ s for s in globals().keys() if s/rg%0]
===============================
['plot3dGr', 'plotTmCh', 'plot3d', 'plotPt', 'plotBode', 'plotTrajectory', 'plot2d', 'plot3dRowCol', 'plotGr', 'plotDgGnPh']
# sympy モジュールのグローバル変数全体から fact を含むものを列挙する
# kre.se.I 引数を追加することで大文字/小文字を区別させない
import sympy as md; rg=krgl('fact',kre.se.I); [ s for s in vars(md).keys() if s/rg%0]
===============================
['factorint', 'factorial2', 'cofactors', 'factorial', 'factor_', 'factor', 'factortools', 'FallingFactorial', 'primefactors', 'factor_list', 'RisingFactorial', 'facts']
このように kre.py の正規表現クラス krgl 使えば、 Perl でのような正規表現の活用の仕方が可能になります。 `
この章では、Zp(N) を八元数化した代数系を扱います。有限体の八元数は、非可換であったり、結合律が成り立たなかったりする代数系ですが、同時に加減乗除が可能な扱いやすい代数系です。コンピュータによる虱潰しテストが可能です。非可換代数系など、広い範囲の代数系の検討がワンライナーで書けて便利です。圏論での Functor, Natural Transformation の具体例をワン・ライナーで記述できてしまいます。
PythonSf には八元数:ClOctornion:oc.Oc: Oc を備えており、非可換な代数での挙動、結合率さえ成り立たない代数での挙動を簡単にコンピュータ上で実行させ試してみることができりす。八元数 Oc だといっても、八個の値の上位側が 0 のときは、それを表示しないので、引数を四つ以下に限定にしてやれば quaternion としての動作になります。引数を二つ以下に限定してやれば複素数の動作になります。次のような具合です。
# 八元数の積
Oc(1,2,3,4,5) Oc(5,0,7)
===============================
Oc(-16, -18, 22, 34, 25, 0, -35, 0)
# 四元数の積
Oc(1,2,3,4) Oc(5,6,7,8)
===============================
Oc(-60, 12, 30, 24)
# 複素数の積
Oc(1,2) Oc(5,6)
===============================
Oc(-7, 16)
この oc.Oc の八元数演算の実装は、愚直に積と和の組み合わせ演算だけでなされています。ですから oc.Oc に 実数以外の体インスタンスを渡してやれば、その一般体の上で、八元数の加減乗除算が実行されてしまいます。すなわち一般体複素数、一般体四元数、一般体八元数の演算が行われるように代数系を拡張できてしまいます。(厳密には ClOctonion は monad として実装してあるわけではなく、Zp(N) との組み合わせしかテストしていません。他の代数系と組み合わせると、細かな問題が出てくるかもしれません。)
体の八元数化による体代数系の拡張はCayley_Dickson_construction ,「ケーリー=ディクソンの構成法」として知られています。
ケーリー=ディクソンの構成法の良いところは拡張された代数系の挙動の予測が付けやすいことです。足し算については、元の体代数系のベクトル足し算になります。積演算については、四元数にしてやることで非可換な代数系が得られます。八元数にしてやることで結合律さえ成り立たない代数系が得られます。
このケーリー=ディクソンの構成法を Zp(N) に適用してやれば、簡単に非可換であったり結合律が成り立たない有限な代数系を作れます。そして有限:小規模な代数系ならばコンピュータで虱潰しに調べ上げられるので便利です。といっても、実際にそのようなプログラムを 0 から作り上げるのは普通の人間では人月単位の仕事になってしまうでしょう。でも PythonSf ならば八元数の要素を Zp(N) インスタンスにしてやるだけで、それを実装できたものとして動いてしまいます。以下のような具合です。
PythonSf ワンライナー
# Zp(3) 四元数
Z3=oc.Zp(3); Oc(Z3(1),Z3(2),Z3(3),Z3(4))
===============================
Oc(1, 2, 0, 1)
pickle exeption
Z3=oc.Zp(3); x=Oc(Z3(1),Z3(2),Z3(1),Z3(4)); 2x, x+x, 3x, x^2, x^-1, x x^-1
===============================
(Oc(2, 1, 2, 2), Oc(2, 1, 2, 2), Oc(0), Oc(1, 1, 2, 2), Oc(1, 1, 2, 2), Oc(1))
pickle exeption
# Zp(127) ランダムな八元数
seed(0); Z127=oc.Zp(127); x=Oc([Z127(a) for a in randi(127,[8])]); 2x, x+x, 3x, x^2, x^-1, x x^-1
===============================
(Oc( 88, 94, 107, 1, 7, 119, 7, 79), Oc( 88, 94, 107, 1, 7, 119, 7, 79), Oc( 5, 14, 97, 65, 74, 115, 74, 55), Oc( 58, 72, 9, 44, 54, 29, 54, 47), Oc( 11, 20, 66, 111, 15, 1, 15, 6), Oc( 1))
pickle exeption
# bi-quaternion:複素数を要素とする四元数
x=Oc(1+2j,3+4j,5+6j,7+8j); 2x, x+x, 3x, x^2, x^-1, x x^-1
===============================
(Oc((2+4j), (6+8j), (10+12j), (14+16j)),
Oc((2+4j), (6+8j), (10+12j), (14+16j)),
Oc((3+6j), (9+12j), (15+18j), (21+24j)),
Oc((30-192j), (-10+20j), (-14+32j), (-18+44j)),
Oc((0.008814413018209996-0.006586594343277799j), (-0.016757070902750873+0.018016272762495157j),
(-0.024699728787291746+0.029445951181712518j), (-0.03264238667183263+0.04087562960092987j)),
Oc((1+3.122502256758253e-17j), -5.551115123125783e-17j, 2.0816681711721685e-17j,
(-2.7755575615628914e-17+2.0816681711721685e-17j)))
# Zp(3) 複素数を要素とする四元数
Z3=oc.Zp(3); x=Oc(Oc(Z3(1),Z3(2)), Oc(Z3(1),Z3(4)), Oc(Z3(5),Z3(6)), Oc(Z3(7),Z3(8))); 2x, x+x, 3x, x^2, x^-1, x x^-1
===============================
(Oc(Oc(2, 1), Oc(2, 2), Oc(1), Oc(2, 1)),
Oc(Oc(2, 1), Oc(2, 2), Oc(1), Oc(2, 1)),
Oc(Oc(0)),
Oc(Oc(2, 1), Oc(1), Oc(1, 2), Oc(0, 2)),
Oc(Oc(0, 2), Oc(2), Oc(2, 1), Oc(0, 1)),
Oc(Oc(1)))
pickle exeption
# 有理式:複素数を要素とする四元数の逆元
s=`s; x=Oc(s+2,3s+4,5s+6,7s+8); for y in (x^-1)[:4]:print(y)
0.0119 s + 0.02381
------------------
2
s + 2.381 s + 1.429
-0.03571 s - 0.04762
-------------------
2
s + 2.381 s + 1.429
-0.05952 s - 0.07143
-------------------
2
s + 2.381 s + 1.429
-0.08333 s - 0.09524
-------------------
2
s + 2.381 s + 1.429
0.0119 s + 0.02381
------------------
2
s + 2.381 s + 1.429
-0.03571 s - 0.04762
-------------------
2
s + 2.381 s + 1.429
-0.05952 s - 0.07143
-------------------
2
s + 2.381 s + 1.429
-0.08333 s - 0.09524
-------------------
2
s + 2.381 s + 1.429
# 有理式四元数の逆元との積が単位元になることを数値実験で確認
s=`s; x=Oc(s+2,3s+4,5s+6,7s+8); x x^-1
===============================
Oc(ClRtnl([ 1.],[ 1.]),
ClRtnl([ 0.],[1]),
ClRtnl([ 0.],[1]),
ClRtnl([ 1.38777878e-17, 0.00000000e+00, 0.00000000e+00],
[ 1. , 2.38095238, 1.42857143]))
oc.Zp(N) インスタンスを要素とする八元数はファイル変数を生成できまないので pickle exeption が発生しています。 oc.Zp(..) は factory 関数であり、引数 N に対応するクラスをダイナミックに生成しているためです。
これでは不便なこともあるので、配布している sfCrrntInii の中で Zp(2),...Zp(7), Zp(127) に相当する静的なクラス Z2,Z3,Z4,Z5,Z6,Z7,Zb を実装してあります。これらを要素とする八元数を O2,O3,O4,O5,O6,O7,Ob として実装してあります。以下、これらについて説明します。
PythonSf ワンライナー
# 非可換な例
O3(1,2,3,0) O3(2,1,0,1)
===============================
Oc(0, 2, 1, 1)
O3(2,1,0,1) O3(1,2,3,0)
===============================
Oc(0, 2, 2, 1)
# 非可換な例を虱潰しに挙げる
lst=[0,1,2]; mi=list( mitr(*([lst]*4)) ); [(tpL,tpR) for tpL,tpR in mitr(mi,mi) if O3(tpL) O3(tpR) != O3(tpR) O3(tpL)]
たくさん
# 可換な例を虱潰しに挙げる
lst=[0,1,2]; mi=list( mitr(*([lst]*4)) ); [(tpL,tpR) for tpL,tpR in mitr(mi,mi) if O3(tpL) O3(tpR) == O3(tpR) O3(tpL)]
たくさん
# 積演算の逆元
1/O3(1,0,2,3)
===============================
(2, 0, 2, 0)
# 逆元が存在しない例
1/O3(1,1,2,3)
snipped
ZeroDivisionError: Square value is 0 at ClOctonion:inv().
# ゼロ因子の例
O3(0,1,1,1) O3(2,0,1,2)
===============================
0
# ゼロ因子を虱潰しに挙げる
# λ x: O3(0,1,1,1) x の Kernel
# 積の単位元は含まれていない
ls=range(3); [ tpl for tpl in mitr(*[ls]*4) if O3(0,1,1,1) O3(tpl) == 0]
===============================
[(0, 0, 0, 0), (0, 1, 1, 1), (0, 2, 2, 2), (1, 0, 2, 1), (1, 1, 0, 2), (1, 2, 1, 0), (2, 0, 1, 2), (2, 1, 2, 0), (2, 2, 0, 1)]
# λ x: O3(0,1,1,1) x の Kernel は積演算について閉じている
ls=range(3); lst=[ tpl for tpl in mitr(*[ls]*4) if O3(0,1,1,1) O3(tpl) == 0]; [ O3(x) O3(y) in lst for x,y in mitr(lst,lst)]
===============================
[True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True]
# λ x: O3(0,1,1,1) x の Kernel は和演算について閉じている
ls=range(3); lst=[ tpl for tpl in mitr(*[ls]*4) if O3(0,1,1,1) O3(tpl) == 0]; [ O3(x)+O3(y) in lst for x,y in mitr(lst,lst)]
===============================
[True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True, True]
# この小さい環の世界でも非可換性は残っている
ls=range(3); lst=[ tpl for tpl in mitr(*[ls]*4) if O3(0,1,1,1) O3(tpl) == 0]; [ O3(x) O3(y) == O3(y) O3(x)in lst for x,y in mitr(lst,lst)]
===============================
[True, True, True, True, True, True, True, True, True, True, True, True, False, False, False, False, False, False, True, True, True, False, False, False, False, False, False, True, False, False, True, False, False, True, False, False, True, False, False, False, True, False, False, False, True, True, False, False, False, False, True, False, True, False, True, False, False, True, False, False, True, False, False, True, False, False, False, False, True, False, True, False, True, False, False, False, True, False, False, False, True]
PythonSf ワンライナー
# 結合律が成り立たない整数八元数の例
O=oc.Oc; a,b,c=O(1,2,3,4,5),O(2,1,4,5,6),O(3,4,1,6,7); str((a b) c), str(a (b c))
===============================
('(-426, -279, 12, -323, -366, -4, 52, 12)', '(-426, -279, 12, -323, -366, -12, 44, -28)')
# 結合律が成り立たない Zp(3) 八元数の例
O=oc.Oc; a,b,c=O(~[1,2,3,4,5,Z3]),O(~[2,1,4,5,6,Z3]),O(~[3,4,1,6,7,Z3]); str((a b) c), str(a (b c))
===============================
('(0, 0, 0, 1, 0, 2, 1, 0)', '(0, 0, 0, 1, 0, 0, 2, 2)')
実数要素の八元数には、積演算された結果の norm が、二つの積要素の norm の積になる特徴があります。この性質は Zp(N) 有限体八元数でも成り立っています。次のような具合です。
PythonSf ワンライナーたち
# 浮動小数点八元数での 積 norm
seed(0); a,b=[Oc(x) for x in randn(2,8)]; f= λ x: (x x.conj())[0]; f(a b), f(a) f(b)
===============================
(47.035939470424147, 47.035939470424154)
# O3 八元数での 積 norm
seed(0); a,b=[O3(x) for x in randint(3,size=[2,8])]; f= λ x: (x x.conj())[0]; f(a b), f(a) f(b)
===============================
(2, 2)
# O7 八元数での 積 norm
seed(0); a,b=[O7(x) for x in randint(7,size=[2,8])]; f= λ x: (x x.conj())[0]; f(a b), f(a) f(b)
===============================
(3, 3)
Zp(N) 四元数はゼロ因子が入り込むことで有限体でなくなって環になります。このゼロ因子が四元数の norm が 0 と同値になりそうです。さらに 0 因子の相手も 0 因子に限定されそうです。このことは O2,O3,O5,O7 四元数について次のように虱潰し数値実験で確認できます。
PythonSf ワンライナーたち
# norm 0 要素はゼロ因子になっている
ls=range(2); is0fctr=λ o: o o.conj() == 0; ls0=[v for v in mitr(*[ls]*4) if is0fctr(O2(v))][1:]; [a for a in ls0 if not O2(0) in [O2(a) O2(x) for x in ls0]]
===============================
[]
ls=range(3); is0fctr=λ o: o o.conj() == 0; ls0=[v for v in mitr(*[ls]*4) if is0fctr(O3(v))][1:]; [a for a in ls0 if not O3(0) in [O3(a) O3(x) for x in ls0]]
===============================
[]
ls=range(4); is0fctr=λ o: o o.conj() == 0; ls0=[v for v in mitr(*[ls]*4) if is0fctr(O4(v))][1:]; [a for a in ls0 if not O4(0) in [O4(a) O4(x) for x in ls0]]
===============================
[]
ls=range(5); is0fctr=λ o: o o.conj() == 0; ls0=[v for v in mitr(*[ls]*4) if is0fctr(O5(v))][1:]; [a for a in ls0 if not O5(0) in [O5(a) O5(x) for x in ls0]]
===============================
[]
ls=range(7); is0fctr=λ o: o o.conj() == 0; ls0=[v for v in mitr(*[ls]*4) if is0fctr(O7(v))][1:]; [a for a in ls0 if not O7(0) in [O7(a) O7(x) for x in ls0]]
===============================
[]
O2,O3,O4,O5,O7 で norm 0 の四元数が 0 因子になることは、次の虱潰しテストで分かります。
PythonSf ワンライナーたち
# norm 0 要素はゼロ因子になっている
ls=range(2); is0fctr=λ o: o o.conj() == 0; ls0=[v for v in mitr(*[ls]*4) if is0fctr(O2(v))][1:]; [a for a in ls0 if not O2(0) in [O2(a) O2(x) for x in ls0]]
===============================
[]
ls=range(3); is0fctr=λ o: o o.conj() == 0; ls0=[v for v in mitr(*[ls]*4) if is0fctr(O3(v))][1:]; [a for a in ls0 if not O3(0) in [O3(a) O3(x) for x in ls0]]
===============================
[]
ls=range(4); is0fctr=λ o: o o.conj() == 0; ls0=[v for v in mitr(*[ls]*4) if is0fctr(O4(v))][1:]; [a for a in ls0 if not O4(0) in [O4(a) O4(x) for x in ls0]]
===============================
[]
ls=range(5); is0fctr=λ o: o o.conj() == 0; ls0=[v for v in mitr(*[ls]*4) if is0fctr(O5(v))][1:]; [a for a in ls0 if not O5(0) in [O5(a) O5(x) for x in ls0]]
===============================
[]
ls=range(7); is0fctr=λ o: o o.conj() == 0; ls0=[v for v in mitr(*[ls]*4) if is0fctr(O7(v))][1:]; [a for a in ls0 if not O7(0) in [O7(a) O7(x) for x in ls0]]
===============================
[]
Zp(N) 四元数積の norm 保持特性より、少なくともゼロ因子の一方は norm が 0 である必要があります。
さらに下の虱潰しテストによる、その相手側も norm が 0 であることが分かります。すなわち norm == 0 であることがゼロ因子の必要条件でもあることが分かります。
PythonSf ワンライナーたち
# ゼロ因子の相手側が norm = 0 になっていない On 四元数全ての集合
# ← 0 x == 0 だから、0 だけは上の条件を無条件で満たす
ls=range(2); is0fctr=λ o: o o.conj() == 0; ls0=[v for v in mitr(*[ls]*4) if is0fctr(O2(v))]; [v for v in ls0 if not { w for w in mitr(*[ls]*4) if O2(v) O2(w) == 0}.issubset(ls0)]
===============================
[(0, 0, 0, 0)]
ls=range(3); is0fctr=λ o: o o.conj() == 0; ls0=[v for v in mitr(*[ls]*4) if is0fctr(O3(v))]; [v for v in ls0 if not { w for w in mitr(*[ls]*4) if O3(v) O3(w) == 0}.issubset(ls0)]
===============================
[(0, 0, 0, 0)]
ls=range(5); is0fctr=λ o: o o.conj() == 0; ls0=[v for v in mitr(*[ls]*4) if is0fctr(O5(v))]; [v for v in ls0 if not { w for w in mitr(*[ls]*4) if O5(v) O5(w) == 0}.issubset(ls0)]
===============================
[(0, 0, 0, 0)]
O6
ls=range(7); is0fctr=λ o: o o.conj() == 0; ls0=[v for v in mitr(*[ls]*4) if is0fctr(O7(v))]; [v for v in ls0 if not { w for w in mitr(*[ls]*4) if O7(v) O7(w) == 0}.issubset(ls0)]
===============================
[(0, 0, 0, 0)]
← 十分ぐらいかかる
ただし、ゼロ因子の相手側がゼロ因子であることは一般の環については成り立ちません。O4 四元数が その反例になります。
PythonSf ワンライナーたち
ls=range(4); is0fctr=λ o: o o.conj() == 0; ls0=[v for v in mitr(*[ls]*4) if is0fctr(O4(v))]; [v for v in ls0 if not { w for w in mitr(*[ls]*4) if O4(v) O4(w) == 0}.issubset(ls0)]
===============================
[(0, 0, 0, 0), (0, 0, 2, 2), (0, 2, 0, 2), (0, 2, 2, 0), (2, 0, 0, 2), (2, 0, 2, 0), (2, 2, 0, 0), (2, 2, 2, 2)]
O4(0, 0, 2, 2) O4(0, 0, 2, 2).conj()
===============================
O4(Z4(0))
ls=range(4); is0fctr=λ o: o o.conj() == 0; ls0=[v for v in mitr(*[ls]*4) if is0fctr(O4(v))]; (0, 0, 2, 2) in ls0
===============================
True
w=O4(0, 0, 2, 2);ls=range(4); is0fctr=λ o: o o.conj() == 0; ls0=[v for v in mitr(*[ls]*4) if is0fctr(O4(v))]; [x for x in mitr(*[ls]*4) if O4(w) O4(x) == 0 and not x in ls0]
===============================
[(0, 0, 1, 1), (0, 0, 1, 3), (0, 0, 3, 1), (0, 0, 3, 3), (0, 2, 1, 1), (0, 2, 1, 3), (0, 2, 3, 1), (0, 2, 3, 3), (1, 1, 0, 0), (1, 1, 0, 2), (1, 1, 2, 0), (1, 1, 2, 2), (1, 3, 0, 0), (1, 3, 0, 2), (1, 3, 2, 0), (1, 3, 2, 2), (2, 0, 1, 1), (2, 0, 1, 3), (2, 0, 3, 1), (2, 0, 3, 3), (2, 2, 1, 1), (2, 2, 1, 3), (2, 2, 3, 1), (2, 2, 3, 3), (3, 1, 0, 0), (3, 1, 0, 2), (3, 1, 2, 0), (3, 1, 2, 2), (3, 3, 0, 0), (3, 3, 0, 2), (3, 3, 2, 0), (3, 3, 2, 2)]
O2,O3,O4,O5,O7 のゼロ因子の集合は積演算に対して閉じていることも、次の虱潰しテストで証明されます。
PythonSf ワンライナーたち
# ゼロ因子同士の積演算は閉じている
ls=range(2); is0fctr=λ o: o o.conj() == 0; ls0=[v for v in mitr(*[ls]*4) if is0fctr(O2(v))]; [(a,b) for a,b in mitr(ls0,ls0) if not O2(a) O2(b) in ls0]
===============================
[]
ls=range(3); is0fctr=λ o: o o.conj() == 0; ls0=[v for v in mitr(*[ls]*4) if is0fctr(O3(v))]; [(a,b) for a,b in mitr(ls0,ls0) if not O3(a) O3(b) in ls0]
===============================
[]
ls=range(4); is0fctr=λ o: o o.conj() == 0; ls0=[v for v in mitr(*[ls]*4) if is0fctr(O4(v))]; [(a,b) for a,b in mitr(ls0,ls0) if not O4(a) O4(b) in ls0]
===============================
[]
ls=range(5); is0fctr=λ o: o o.conj() == 0; ls0=[v for v in mitr(*[ls]*4) if is0fctr(O5(v))]; [(a,b) for a,b in mitr(ls0,ls0) if not O5(a) O5(b) in ls0]
===============================
[]
ls=range(7); is0fctr=λ o: o o.conj() == 0; ls0=[v for v in mitr(*[ls]*4) if is0fctr(O7(v))]; [(a,b) for a,b in mitr(ls0,ls0) if not O7(a) O7(b) in ls0]
===============================
[]
O3 四元数が非可換であることは次の例で証明できます。
PythonSf ワンライナー
# O3 四元数積の非可換な例
a,b=(O3(0, 0, 0, 1), O3(0, 0, 1, 0)); a b, b a
===============================
(O3(0, 2), O3(0, 1))
でも O2 八元数,O4 四元数は可換であることが次のように証明できます。
PythonSf ワンライナー
ls=range(4); ls4=[ O2(v) for v in mitr(*[ls]*4)]; [ (x,y) for x,y in mitr(ls4,ls4) if (x y) != (y x)]
python -u -m sfPP "ls=range(4); ls4=[ O2(v) for v in mitr(*[ls]*4)]; [ (x,y) for x,y in mitr(ls4,ls4) if (x y) != (y x)]"
===============================
[]
← 一分ぐらいかかります。
python -u -m sfPP "ls=[Z2(0),Z2(1)]; ls4=[ O2(v) for v in mitr(*[ls]*8)]; [ (x,y) for x,y in mitr(ls4,ls4) if (x y) != (y x)]"
time:21:31
===============================
[]
← 半日かかります。
でも、O4 八元数は非可換であることが次のように分かります。
PythonSf ワンライナー
N=3; seed(0);mt=randint(4,size=[N,2,8]); `print([ (x,y) for x,y in mt if O4(x) O4(y) != O4(y) O4(x)])
[(ClTensor([0, 3, 1, 0, 3, 3, 3, 3], dtype=int),
ClTensor([1, 3, 1, 2, 0, 3, 2, 0], dtype=int)),
(ClTensor([0, 0, 2, 1, 2, 3, 3, 2], dtype=int),
ClTensor([0, 1, 1, 1, 1, 0, 1, 0], dtype=int)),
(ClTensor([3, 0, 3, 1, 2, 3, 3, 0], dtype=int),
ClTensor([2, 3, 0, 1, 3, 1, 3, 3], dtype=int))]
===============================
None
標準配布のカレント・ディレクトリの sfCrrntIni.py ファイルには圏論を扱うための dom, cod を扱えるようにする CT クラス、関数 fCT(..) が実装されています。圏論で頻出する monoid 構造を扱うため:即ち二項関数を扱うための関数 f2CT(..) も設けてあります。また~% user 演算子を関数合成操作に割り当ててあります。さらに Z2,Z3,Z4,Z5,Z5 有限体クラス、 O2,O3,O4,O5,O7 有限八元数クラスを設けてあります。これらを使って、圏論における様々の具体例を実際に計算できる PythonSf one-liner 式として表現できます。
クラス CT は関数の入出力パラメータのタイプを指定するクラスです。Python でも、C や Java 言語での float function(int) のような、関数の型指定を可能にします。例えば CT(int,float) で、入力が int タイプの引数であり、戻り値が float タイプの関数型指定を行うクラスのインスタンスを作ります。
PythonSf ワンライナー
CT(int, float)
===============================
でも CT(...) インスタンスを作っただけでは、それは型を保持しているクラス CT のインスタンスにすぎません。まだ関数には言及していないからです。 上のインスタンスに対し関数を渡してやると、int 引数を与えて、float 結果を返すことを確認する作業が追加された関数を返します。int を与えて float が返る動作をしているときは、下のように普通の動作をします。
PythonSf ワンライナー
ct=CT(int, float); f=ct(λ x:x+1.5); f(3)
===============================
4.5
でも、入力パラメータまたは出力結果の型が指定と異なるとき、次のように例外が発生します。
PythonSf ワンライナー
ct=CT(int, float); f=ct(λ x:x+1.5); f(3.1)
Traceback (most recent call last):
File "C:\Python27\lib\runpy.py", line 162, in _run_module_as_main
"__main__", fname, loader, pkg_name)
File "C:\Python27\lib\runpy.py", line 72, in _run_code
exec code in run_globals
File "D:\my\vc7\mtCm\sfPP.py", line 2, in
pysf.sfPPrcssr.start()
File "pysf\sfPPrcssr.py", line 2741, in start
__execLine( (" ".join(sys.argv[1:])).strip() )
File "pysf\sfPPrcssr.py", line 2357, in __execLine
valStt = eval(ustConvertedAt, globals(), locals() )
File "", line 1, in
File "sfCrrntIni.py", line 230, in _
+ str(sqAg[k])
File "sfCrrntIni.py", line 85, in Assert
raise sf.ClAppError(strAg)
pysf.sfFnctns.ClAppError: Error at CT:__call__(..) input type check:3.1
入力引数や戻り値の型は、リストで型を指定することで複数の引数値に対応させます。また型指定には集合や True/False 値を返す関数を使うことも可能です。下のような具合です
PythonSf ワンライナー
ct=CT([int, float,{7,8,9},λ x:isinstance(x,complex)], complex); f=ct(λ x,y,z,t:x+y+z+6+1.5j); f(3,4.1, 7, 2j)
===============================
(20.1+1.5j)
ct=CT([int, float,{7,8,9},λ x:isinstance(x,complex)], complex); f=ct(λ x,y,z,t:x+y+z+6+1.5j); f(3,4.1, 5, 2j)
Traceback (most recent call last):
File "C:\Python27\lib\runpy.py", line 162, in _run_module_as_main
"__main__", fname, loader, pkg_name)
File "C:\Python27\lib\runpy.py", line 72, in _run_code
exec code in run_globals
File "D:\my\vc7\mtCm\sfPP.py", line 2, in
pysf.sfPPrcssr.start()
File "pysf\sfPPrcssr.py", line 2741, in start
__execLine( (" ".join(sys.argv[1:])).strip() )
File "pysf\sfPPrcssr.py", line 2357, in __execLine
valStt = eval(ustConvertedAt, globals(), locals() )
File "", line 1, in
File "sfCrrntIni.py", line 230, in _
+ str(sqAg[k])
File "sfCrrntIni.py", line 85, in Assert
raise sf.ClAppError(strAg)
pysf.sfFnctns.ClAppError: Error at CT:__call__(..) input type check:5
、その constructor で
上の CT クラスによる型指定機能は、圏論の dom/cod を明示するのに役立ちます。でもワン・ライナーで使うには CT クラスのインスタンスを毎度作らねばならず面倒です。なので下のような fCT(...) 関数を設けてあります。
PythonSf ワンライナー
np.source(fCT)
In file: sfCrrntIni.py
def fCT(f, inputTypeOrSqTypeAg=None, outTypeAg=None):
ctAt = CT(inputTypeOrSqTypeAg, outTypeAg)
return ctAt(f)
===============================
None
下のように使います。ちなみに type がデフォルトの None で指定されているときは、型チェックを行わないことを意味します。
PythonSf ワンライナーたち
f=fCT(λ x:x+1, Z3); f(Z3(2))
===============================
Z3(0)
f=fCT(λ x:x+1.5, int); f(0)
===============================
1.5
圏論で頻出する monoid のために二項関数の型指定を行う f2CT(..) も sfCrrntIn.py に実装しています。通常使うのは fCT(..) ではなく f2CT(..) になると思います。Curry 化された closure 関数を f2CT(..).fst(引数), f2CT(..).lst(引数) だけで生成できます。
PythonSf ワンライナー
np.source(f2CT)
In file: sfCrrntIni.py
def f2CT(f, ty=None, tyOut=None):
# comment
if ty==None and tyOut==None:
return fCT(f,[None,None],tyOut)
elif ty!=None and tyOut==None:
return fCT(f, [ty,ty], ty)
else:
# ty!=None and tyOut!=None:
return fCT(f, [ty,ty], tyOut)
===============================
None
下のように使います。ちなみに f2CT(..) のときは、戻り値の型をデフォルト None のままにしておくことは、戻り値の型が入力値の型と同じであることを意味しています。
PythonSf ワンライナーたち
f=f2CT(λ x,y:x+y, Z3); f(Z3(1), Z3(2))
===============================
Z3(0)
f=f2CT(λ x,y:x+y, Z3); f.dom, f.cod
===============================
((, ), (,))
f=f2CT(λ x,y:x+y+0.5, int, float); f(1, 2)
===============================
3.5
f=f2CT(λ x,y:x+y, int, float); f(1, 2)
Traceback (most recent call last):
File "C:\Python27\lib\runpy.py", line 162, in _run_module_as_main
"__main__", fname, loader, pkg_name)
File "C:\Python27\lib\runpy.py", line 72, in _run_code
exec code in run_globals
File "D:\my\vc7\mtCm\sfPP.py", line 2, in
pysf.sfPPrcssr.start()
File "pysf\sfPPrcssr.py", line 2741, in start
__execLine( (" ".join(sys.argv[1:])).strip() )
File "pysf\sfPPrcssr.py", line 2357, in __execLine
valStt = eval(ustConvertedAt, globals(), locals() )
File "", line 1, in
File "sfCrrntIni.py", line 256, in _
+ str(valAt)
File "sfCrrntIni.py", line 85, in Assert
raise sf.ClAppError(strAg)
pysf.sfFnctns.ClAppError: Error at CT:__call__(..) output type check:3
CT クラスを使って関数の入出力型を指定できることは、圏論の dom/cod を明示する意味で便利です。でも C/C++/Java でのように、プログラム全体に渡る整合性の確認を行わせる型指定の便利さまでは享受できません。Python では全ての関数で型指定・チェックが行われるわけではないからです。CT に過度に期待すべきではありません。また圏論での PythonSf 式による検討で、型チェックを行わずに済ますことも多くあります。PythonSf 式を書いている本人にとって dom/cod は文脈上自明であることが多く、型指定なしの方が、PythonSf 式記述を少し楽にできるからです。
圏論の議論では Curry 化関数になっている CT クラスの fst,lst メンバーのほうが、型指定よりも便利に使えるでしょう。fst は最初の引数の、lst は最後の引数の Curry 化関数です。次のように使います。
PythonSf ワンライナーたち
f=f2CT(λ x,y:x+2y, Z3); [f.fst(Z3(1))(Z3(x)) for x in range(5)]
===============================
[1, 0, 2, 1, 0]
f=f2CT(λ x,y:x+2y, Z3); [f.lst(Z3(1))(Z3(x)) for x in range(5)]
===============================
[2, 0, 1, 2, 0]
圏論で頻出する関数合成のために sfCrrntIni.py で、ユーザー演算子:~% に関数合成の機能をアサインしてあります。下のコードで実装されています。
# ~%: user 演算子に関数合成
k__tilda__UsOp_mul____ = lambda x,y:Oc(sf.krry((Oc(x) * Oc(y)).m_tpl, Z5)) # ~*
これにより、例えば二変数関数:Z3 の積 の fst 関数の合成が、Z3 での積に対応することを示す例を、ワン・ライナーで作れます。
PythonSf ワンライナー
# f.fst(Z3(2)) と f.fst(Z3(2)) の関数合成が f.fst(Z3(2) Z3(2)) であることの確認
ls=[Z3(k) for k in range(3)]; f=f2CT(λ x,y:x y, Z3); [(f.fst(Z3(2)) ~% f.fst(Z3(2)))(x) == f.fst(Z3(2) Z3(2))(x) for x in ls]
===============================
[True, True, True]
Abstract nonsence と揶揄されることもある圏論なんかを、何が嬉しくてやるのかと言えば、集合論が弱すぎるからです。集合論では対象の構造を論じるのに {式(x) for x in ... } しかありません。あとは自然言語で補足・記述していくことになります。
圏論は集合に結合律を満たす arrow 構造を追加します。集まりの性質しかなかった集合に、arrow:関数構造を付け加えることで、豊穣な構造を持った集合が扱えるようになります。また arrow により対象の構造を視覚化できます。数学の世界では広く出てくる結合律による縛りが、豊富なグラフ構造をもたらします。
圏論のイントロダクションとして McLane が書いた圏論の教科書のイントロダクションに書いてあるものが旨く書けていると思います。ここの 4 ページ目で読めます。
ただし大部分の方にとって、このイントロダクション部分だけでは何を言っているのか、分かりにくいと思います。もっとも Web 全体を見渡しても、これ以上に良く書けた圏論のイントロダクションも少ないとも思います。それだけ圏論の説明は難しいのだと思います。
これらの説明が難しいのは、どうしても category theory で扱う対象が複雑になってしまうことが大きいと思います。具体例を提示しようとすると tesor of aberian groups のような、職業数学者にしか分からないものになりがちです。
でも PythonSf の Category Theory で使えるツールを使えば、これらの例の多くを記述できます。すなわち、言葉で説明されいるだけでなく、実際にコンピュータ上で動かせる具体例です。ですから、言葉だけの説明での曖昧性が入り込む余地のない具体例です。しかも、これらの多くがワン・ライナーで書けてしまいます。
以下 MacLane の教科書のイントロダクション部分を PythonSf を使って説明していきます。
集合論の範囲で {1,2} と {5,6,7} の直積集合は {(x,y) such that x∈{1,2},y∈{5,6,7} } とでも書くでしょう。PythonSf ならば次のように書けます。
PythonSf ワンライナーたち
# 集合 X,Y の直積集合 XxY を PythonSf 式で作る
X,Y={1,2},{5,6,7}; XxY={(x,y) for x,y in mitr(X,Y)}; XxY
===============================
set([(2, 7), (2, 6), (1, 5), (1, 6), (1, 7), (2, 5)])
# XxY を kfs frozenset にしてみる
X,Y={1,2},{5,6,7}; XxY=kfs([(x,y) for x,y in mitr(X,Y)]); XxY
===============================
kfs([(1, 5), (1, 6), (1, 7), (2, 5), (2, 6), (2, 7)])
(kfs:frozenset を使うと、その集合の中身が sorting されているので便利です。一方で {... ..} の集合記述も数学での表記に近く、記述も簡素です。以下では両方の集合記述が混在されて使われます。)
集合論での直積集合は要素ペアが示されるだけです。その働きは自然言語で不明瞭に説明されるだけです。集合論は直積のような数学的対象を記述する道具として弱すぎます。下のような、直積集合:XxYから X への自明な写像は明白だからと説明もされないことのほうが多いでしょう。
PythonSf ワンライナー
X,Y={1,2},{5,6,7}; XxY=kfs([(x,y) for x,y in mitr(X,Y)]); fXxY_X=fCT(λ tpl:tpl[0], XxY, X); fXxY_X((1,5))
===============================
1
圏論では集合 X と Y の直積集合 XxY は下のグラフで視覚化される、arrow p,q を伴った構造だと定義されます。
圏論での直積集合 XxY
{1,2} p q {5,6,7}
X ←─ XxY ──→ Y
↑ ↑ ↑
│ │∃!h │
│ │ │
└───W ────┘
f g
すなわち「(集合:XxY, arrow:p, arrow:q) が集合 X,Y の直積集合である」とは「任意の集合 W と f:W→X, g:W→Y 関数が与えられたとき、h:W→XxY がユニークに存在し f == h〇p, g== h〇q とできる」ことであるとされます。
こんな抽象的な言葉だけでは普通の人間では正しく理解できません。PythonSf を使って具体例を作ってみましょう。X,Y={1,2},{5,6,7} 二つの直積集合 XxY を dom とし、X,Y を cod とする p,q arrow 関数を下のように与えることで、圏論的な直積集合の定義の具体例を作れます。
PythonSf ワンライナー
X,Y={1,2},{5,6,7}; XxY=kfs([(x,y) for x,y in mitr(X,Y)]);p,q=fCT(λ x_y:x_y[0],XxY,X), fCT(λ x_y:x_y[1],XxY,Y)
===============================
(, )
上の XxY,p,q に対し、下のように W={0,1} 集合と arrow f,g を下のように与えてみます。
PythonSf ワンライナー
X,Y={1,2},{5,6,7}; XxY=kfs([(x,y) for x,y in mitr(X,Y)]);p,q=fCT(λ x_y:x_y[0],XxY,X), fCT(λ x_y:x_y[1],XxY,Y); W={10,11}; f,g=fCT(λ x:1,W,X), fCT(λ x:5+x%2,W,Y)
===============================
(<function _ at 0x02C6F430>, <function _ at 0x02C6F3B0>)
X,Y={1,2},{5,6,7}; XxY=kfs([(x,y) for x,y in mitr(X,Y)]);p,q=fCT(λ x_y:x_y[0],XxY,X), fCT(λ x_y:x_y[1],XxY,Y); W={10,11}; f,g=fCT(λ x:1,W,X), fCT(λ x:5+x%2,W,Y); [f(x) for x in W]
===============================
[1, 1]
X,Y={1,2},{5,6,7}; XxY=kfs([(x,y) for x,y in mitr(X,Y)]);p,q=fCT(λ x_y:x_y[0],XxY,X), fCT(λ x_y:x_y[1],XxY,Y); W={10,11}; f,g=fCT(λ x:1,W,X), fCT(λ x:5+x%2,W,Y); [g(x) for x in W]
===============================
[5, 6]
この適当に与えられた W,f,g に対し次のような ∃!h:W→XxY を作れます。
PythonSf ワンライナー
X,Y={1,2},{5,6,7}; XxY=kfs([(x,y) for x,y in mitr(X,Y)]);p,q=fCT(λ x_y:x_y[0],XxY,X), fCT(λ x_y:x_y[1],XxY,Y); W={10,11}; f,g=fCT(λ x:1,W,X), fCT(λ x:5+x%2,W,Y); dh={10:(1,5),11:(1,6)}; h=fCT(λ x:dh[x],W,XxY); [h(x) for x in W]
===============================
[(1, 5), (1, 6)]
このように与えられた h に対し先の直積集合のグラフが成り立つこと:arrow が commute することを次のように確認できます
PythonSf ワンライナーたち
# f と p〇h が commute する
X,Y={1,2},{5,6,7}; XxY=kfs([(x,y) for x,y in mitr(X,Y)]);p,q=fCT(λ x_y:x_y[0],XxY,X), fCT(λ x_y:x_y[1],XxY,Y); W={10,11}; f,g=fCT(λ x:1,W,X), fCT(λ x:5+x%2,W,Y); dh={10:(1,5),11:(1,6)}; h=fCT(λ x:dh[x],W,XxY); [f(x) == (p~%h)(x) for x in W]
===============================
[True, True]
# g と q〇h が commute する
X,Y={1,2},{5,6,7}; XxY=kfs([(x,y) for x,y in mitr(X,Y)]);p,q=fCT(λ x_y:x_y[0],XxY,X), fCT(λ x_y:x_y[1],XxY,Y); W={10,11}; f,g=fCT(λ x:1,W,X), fCT(λ x:5+x%2,W,Y); dh={10:(1,5),11:(1,6)}; h=fCT(λ x:dh[x],W,XxY); [g(x) == (q~%h)(x) for x in W]
===============================
[True, True]
この h 関数:arrow が与えられた W,f,g に対してユニークに定まることは虱潰しによる確認で証明できます。でも煩雑になりすぎるので省略します。自明に近いとも思います。
圏論の直積集合の定義ならば、集合 WW:{0,1,2,3,4,5} も X,Y の直積集合に分割できます。次のような pp,qq を考えて見ましょう。
# 圏論での直積集合
{0,1,2,3,4,5,6}
{1,2} pp qq {5,6,7}
X ←─ WW ──→ Y
↑ ↑ ↑
│ │∃!h │
│ │ │
└───W ────┘
f g
PythonSf ワンライナー
# pp:WW→X
X,Y={1,2},{5,6,7}; WW=kfs(range(6));pp,qq=fCT(λ x_y:1 if x_y<3 else 2,WW,X), fCT(λ x_y:5+x_y%3,WW,Y); W={10,11}; [pp(x) for x in WW]
===============================
[1, 1, 1, 2, 2, 2]
# qq:WW→Y
X,Y={1,2},{5,6,7}; WW=kfs(range(6));pp,qq=fCT(λ x_y:1 if x_y<3 else 2,WW,X), fCT(λ x_y:5+x_y%3,WW,Y); W={10,11}; [qq(x) for x in WW]
===============================
[5, 6, 7, 5, 6, 7]
上のような X,Y,WW,pp,qq に対し、先ほどの f,g に対応する ∃!h を次のように定義しましょう
PythonSf ワンライナー
X,Y={1,2},{5,6,7}; WW=kfs(range(6));pp,qq=fCT(λ x_y:1 if x_y<3 else 2,WW,X), fCT(λ x_y:5+x_y%3,WW,Y); W={10,11}; f,g=fCT(λ x:1,W,X), fCT(λ x:5+x%2,W,Y); dh={10:0,11:1}; h=fCT(λ x:dh[x],W,WW); [h(x) for x in W]
===============================
[0, 1]
上の ∃!h と {0,1,2,3,4,5} に対し、下のように直積構造が成立することを確認できます。
PythonSf ワンライナー
# f と pp〇h が commute する
X,Y={1,2},{5,6,7}; WW=kfs(range(6));pp,qq=fCT(λ x_y:1 if x_y<3 else 2,WW,X), fCT(λ x_y:5+x_y%3,WW,Y); W={10,11}; f,g=fCT(λ x:1,W,X), fCT(λ x:5+x%2,W,Y); dh={10:0,11:1}; h=fCT(λ x:dh[x],W,WW); [f(x)==(pp~%h)(x) for x in W]
===============================
[True, True]
# g と qq〇h が commute する
X,Y={1,2},{5,6,7}; WW=kfs(range(6));pp,qq=fCT(λ x_y:1 if x_y&;t;3 else 2,WW,X), fCT(λ x_y:5+x_y%3,WW,Y); W={10,11}; f,g=fCT(λ x:1,W,X), fCT(λ x:5+x%2,W,Y); dh={10:0,11:1}; h=fCT(λ x:dh[x],W,WW); [g(x)==(qq~%h)(x) for x in W]
===============================
[True, True]
圏論の直積集合の定義を導入することで {0,1,2,3,4,5} のような直積集合とは思えない集合も {1,2} と {5,6,7} の直積集合とみなせるようになりました。これにより直積集合に関する多くの性質が {0,1,2,3,4,5} 集合についても成り立ちます。このことは {0,1,2,3,4,5} 集合に直積集合の構造を導入したとも言えます。圏論の威力を示す例だとも思います。皆様はどのように思われるでしょうか。
直積での議論でも示されたように、圏論での構造は有向グラフ構造として可視化されます。この有向グラフの向きを反転させたものが存在します。product:直積集合の有向グラフを反転させたものが存在し co-product 集合と呼ばれています。
p q
X──→ XuY ←──Y
│ l │
│ l∃!h │
│ l │
│ V │
└──→ W ←──┘
f g
f,g are given
ただし co-product の具体例は複数存在することが普通であり、与えられた morphing 関数 f,g に対して ∃!h が存在するだけで意味のないものも多くあります。というより意味もない co-product のほうが普通であり、意味のある co-product や co-???? を見つけ出すのが研究者だと言えます。
少し屁理屈に近い面があるとも思いますが X,Y={1,2},{5,6,7} の直積:product に対して co-product:XuY,p:X→XuY,q:Y→XuY を構成してみましょう。
PythonSf ワンライナー
X,Y=kfs({1,2}),kfs({5,6,7}); XuY=X+Y; p=fCT(λ x:x, X, XuY); q=fCT(λ y:y, Y, XuY); (XuY,p,q)
===============================
(kfs([1, 2, 5, 6, 7]), , )
下のように p,q 関数は動作します。
PythonSf ワンライナー
X,Y=kfs({1,2}),kfs({5,6,7}); XuY=X+Y; p=fCT(λ x:x, X, XuY); q=fCT(λ y:y, Y, XuY); [p(x) for x in X], [q(y) for y in Y]
===============================
([1, 2], [5, 6, 7])
関数 p の dom, cod は下のようになっています。
PythonSf ワンライナー
X,Y=kfs({1,2}),kfs({5,6,7}); XuY=X+Y; p=fCT(λ x:x, X, XuY); q=fCT(λ y:y, Y, XuY); p.dom, p.cod
===============================
((kfs([1, 2]),), (kfs([1, 2, 5, 6, 7]),))
集合 W として kfs({10,11,12}) を想定し、関数 f:X→W:λ x:10+x, g:Y→W:λ y:5+y が与えられたとしましょう。h=λ z: 10+z if z <= 2 else 5+z が、上の co-product の有効グラフの commutability を満たします。次のように確認できます。
PythonSf ワンライナーたち
X,Y=kfs({1,2}),kfs({5,6,7}); XuY=X+Y; p=fCT(λ x:x, X, XuY); q=fCT(λ y:y, Y, XuY); f,g,h=fCT(λ x:10+x), fCT(λ y:5+y), fCT(λ z: 10+z if z <= 2 else 5+z);[(h ~% p)(x) == f(x) for x in X]
===============================
[True, True]
X,Y=kfs({1,2}),kfs({5,6,7}); XuY=X+Y; p=fCT(λ x:x, X, XuY); q=fCT(λ y:y, Y, XuY); f,g,h=λ x:10+x, λ y:5+y, λ z: 10+z if z <= 2 else 5+z; [(h ~% p)(x) == f(x) for x in X]
===============================
[True, True]
Cartesian product:直積集合に対して、その co-product は和集合に対して作れることが面白いと思います。何かのときに利用できそうな気がします。
この co-product 和集合が作れることには、二つの集合が互いに素であることが利いています。互いに素でないと、関数 h を λ z: 10+z if z <= 2 else 5+z のようには作れません。圏論の教科書では X と Y が素でないときは無理やりに素にする方法が書かれているのですが、私には屁理屈としか思えません。
Category の公理は単純です。functor と natural transformation は category theory の肝でしょう。これを前提に、抽象 category theory を構築していくのですから。
でも、これらの定義を見ても、何を言っているのかさっぱり分からんのが普通の人間でしょう。MacLane の教科書でも、これらの定義の直後に幾つかの具体例を示してくれるのですが、
下の fO5toO3 は O5 から O3 への圏に関連する関手や自然変換の具体例を記述するのに使えます。
●関手 Z5 O5 複素数 │ │ ↓ ↓ Z3 O3 複素数 ●自然変換 Z5 O5 複素数 ─→ O5 四元数 │ │ │ ↓ ↓ ↓ Z3 O3 複素数 ─→ O3 四元数
PythonSf ワンライナー
fO5toO3 = fCT(λ x:O3(x.m_tpl), O5, O3); fO5toO3(O5(1,2,3,4))
===============================
(1, 2, 0, 1)
fO5toO3 = fCT(λ x:O3(x.m_tpl), O5, O3); fO5toO3.dom, fO5toO3.cod
===============================
((,), (,))
fO5toO3 = fCT(λ x:O3(x.m_tpl), O5, O3); fO5toO3(O3(1,2,6,4))
Traceback (most recent call last):
File "C:\Python27\lib\runpy.py", line 162, in _run_module_as_main
"__main__", fname, loader, pkg_name)
File "C:\Python27\lib\runpy.py", line 72, in _run_code
exec code in run_globals
File "D:\my\vc7\mtCm\sfPP.py", line 2, in
pysf.sfPPrcssr.start()
File "pysf\sfPPrcssr.py", line 2739, in start
__execLine( (" ".join(sys.argv[1:])).strip() )
File "pysf\sfPPrcssr.py", line 2355, in __execLine
valStt = eval(ustConvertedAt, globals(), locals() )
File "", line 1, in
File "sfCrrntIni.py", line 155, in _
+ str(sqAg[k])
File "sfCrrntIni.py", line 37, in Assert
raise sf.ClAppError(strAg)
pysf.sfFnctns.ClAppError: Error at CT:__call__(..) input type check:(1, 2, 0, 1)
fO5toO3 と product, sum を組み合わせた操作は、 O5 から O3 への圏に関連するより単純な関手や自然変換の具体例を記述するのに使えます。
●関手 Z5 O5 複素数 │ │ ↓ ↓ Z3 Z3 ●自然変換 Z5 O5 複素数 ─→ O5 四元数 │ │ │ ↓ ↓ ↓ Z3 Z3 ─→ Z3
ただし product は八元数での product になっており、四元数に適用すると、上位の 0 が掛かってしまって その値は 0 になってしまう。明示的に slice してやらねばならない。
PythonSf ワンライナー
# sum は OK
sum(O3(1,2,3,4))
===============================
1
# product は 0 になってしまう。
product(O3(1,2,1,4))
===============================
0
# slice を介在させる
product(O3(1,2,1,4)[:4])
===============================
2
圏論を使うことで、複数の分野に散在していた抽象概念を、さらなる高みから統一して把握しなおすことが可能になります。これは研究者など「新たな概念を生み出す」者たちに強力なツールをもたらします。抽象的に頭の中だけでボンヤリと考えていたことがらにグラフを使って可視化された具体的な全体構造を見通せるようになるからです。
圏論は大学等の研究者に限らす「新たな概念を生み出す」者たち全てが利用できる強力ツールです。例えば PythonSf の基本関数たち(sin, cos や `X 恒等関数など)は「リカーシブに加減乗除算と整数べき乗算が可能」です。この「リカーシブに加減乗除と整数べき乗算が可能」な構造は monad とみなせます。「リカーシブに加減乗除算と整数べき乗算が可能」にしているのは ClAF クラスが実装しています。この実装仕様を定めるのに monad 構造を意識しているか否かは全体を見通す力に決定的な違いをもたらします。
圏論なんて abstract nonsence だと思われている方もいると思います。でも「新たな概念を生み出す者」であることを望むならば、学んでおくべき新しい道具です。それを学ぶ手間隙以上に価値のある強力な道具を手に入れられます。
下の回路の伝達関数を考えます。
┌──┐
┌─┤ Zf ├─┐
│ └──┘ │
┌─┐→│Vm │
Vi ─┤Zi├─┴─◆- │
└─┘Ii │G >──┴─── Vo
┌─◇+
│
│
≡
下の関係式がなりたちます。
Vo = -G Vm ----------- (1)
Vi-Vm = Zi Ii --------- (2)
Vm - Vo = Zf Ii ------- (3)
Vo/Vi の伝達関数が欲しいので、下の PythonSf 式で symbolic な代数解を計算させます。
PythonSf ワンライナー
ts(); Vi,Vo,Vm, Ii, Zi,Zf, G = ts.symbols('Vi,Vo,Vm, Ii, Zi,Zf, G'); ts.solve([ts.Eq(Vo+G Vm), ts.Eq(Vi-Vm-Zi Ii), ts.Eq(Vm-Vo-Zf Ii)], [Vo,Vm,Ii])
===============================
{Vo: G*Vi*Zf/(-G*Zi - Zf - Zi), Ii: Vi*(G + 1)/(G*Zi + Zf + Zi), Vm: Vi*Zf/(G*Zi + Zf + Zi)}
上の代数解より、Vo と Vi には下の関係式が成り立つことが解ります。
Vo==-G Vi Zf/(G Zi + Zf + Zi)
==- Vi Zf/( Zi + (Zf + Zi)/G ) --------- (4)
∴
Vo/Vi == -Zf/(Zi + (Zf + Zi)/G ) ----------- (5)
G が無限大のとき
Vo/Vi == -Zf/Zi ----------------------------- (6)
さて代表的なオペアンプ uA741 の DC ゲインは 25000 倍であり、その GBW は 1MHz です。そのファイル変数 uA741.pvl を下のように作っておきましょう。後で上の G に代入する形で使います。
PythonSf ワンライナー
f=1 M` Hz`; uA741:=2pi f/(`s + 2pi f/25000)
===============================
6.283e+06
---------
s + 251.3
PythonSf ワンライナー
G=:uA741; G.plotBode(0.1Hz`, 10M` Hz`)
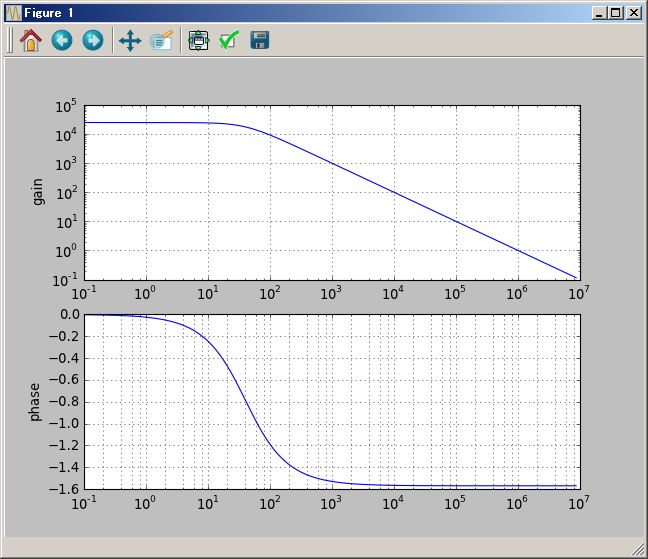
下のような回路の特性を検討してみましょう
C1:0.001uF
┌──┤├──┐
│ R2:10kΩ │
├──MWMW──┤
Ii R1:1kΩ C1:0.1uF│ │
───MWMW──┤├──┴─◆- │
Vi Vm │ G>──┴───
┌─◇+ uA741
│
│
≡
理想オペアンプのとき、(6) 式より、上の回路の周波数特性は次のようになります。(下の式で ~+ 演算子は並列接続での足し算を計算させています)
PythonSf ワンライナー
R1,R2,C1,C2=1kΩ`,10kΩ`,0.1uF`,0.001uF`; Zi,Zf = R1+1/(C1 `s), R2~+(1/(C2 `s)); (-Zf/Zi ).plotBode(10 Hz`, 10 M` Hz`)

uA741 オペアンプのとき、(5)式より上の回路の周波数特性は次のようになります。ゲイン特性が 1MHz 近辺で異なります。位相特性は、100kHz ぐらいから違ってきています。
PythonSf ワンライナー
G=:uA741; R1,R2,C1,C2=1kΩ`,10kΩ`,0.1uF`,0.001uF`; Zi,Zf = R1+1/(C1 `s), R2~+(1/(C2 `s)); ( -Zf/(Zi + (Zf + Zi)/G ) ).plotBode(10 Hz`, 10 M` Hz`)
理想オペアンプと uA741 でのステップ応答の違いを見てみましょう
PythonSf ワンライナー
G=:uA741; R1,R2,C1,C2=1kΩ`,10kΩ`,0.1uF`,0.001uF`; Zi,Zf = R1+1/(C1 `s), R2~+(1/(C2 `s)); ( -Zf/Zi ).plotAnRspns(0.3ms`); ( -Zf/(Zi + (Zf + Zi)/G ) ).plotAnRspns(0.3ms`, color=red)
赤い線のほうが uA741 側です。当然ながら uA741 のステップ応答のほうが少し鈍ります。でも多くの場合で許されそうな範囲です。
厳密には uA741 の slew rate は 0.5V/us 程度ですから、そっちの方の影響の方が少しだけ強そうです。もし slew rate まで含めてシミュレートしようとすると、PythonSf ではなく Spice を持ち出してくるべきでしょう。PythonSf でも kOde(..) を使って微分方程式を解かせればシミュレートできます。でも その微分方程式モデルを作り上げる手間が面倒すぎです。
逆に線形系:Laplace 変換で扱える範疇ならば、上の程度の回路の特性検討は Spice よりも PythonSf の方が便利だと思います。Spice ソフトを立ち上げたり、回路図を描いて部品定数を入力するのではなく、エディタ上で PythonSf 式を書くだけなのですから。
もう少し複雑な下の回路トポロジで記述される多重帰還型バンドパスフィルタを検討してみましょう。
Io
┌──────┬──────┐
│ │ Vo │
┌─┴─┐ ┌─┴─┐ │
│ Z3 │ │ Z5 │ │
└─┬─┘ └─┬─┘ │
│↑I2 →│ │
Ii ┌──┐ │V2┌──┐Im│ │
─┤ Z1 ├──┼─┤ Z4 ├─┴──◆- Vo│
Vi └──┘ ↓│Ig└──┘Vm │ G>─┴───
┌─┴─┐ ┌─◇+
│ Z2 │ │
└─┬─┘ │
≡ ≡
上の Vi,Vo と Z1, Z2,Z3,Z4,Z5 と V2,Vm,I2,Ig,Im の間に次の六つの関係式が成り立ちます。
Vm = - 1/G Vo ---------------------------------------(1)
Im = (1+1/G) Vo/Z5 --------------------------------- (2)
I2 = 1/Z3 (V2-Vo) ---------------------------------- (3)
Im = 1/Z5 (V2-Vm) ---------------------------------- (4)
Vi-V2 = Z1 I2 + Z1 Im + Z1 Ig ---------------------- (5)
V2 = Vm + Im Z4
= -1/G Vo + (1+1/G) Vo Z4/Z5 -------------------- (6)
上の関係式から V2, Im,Ig,Vm を消去して Vo/Vi を表す式を求めるため、下の PythonSf 式を使って Vo,V2, Im,Ig,Vm を Vi と Z1,Z2,Z3,Z4,Z5 の組み合わせの式に変形します。その結果の Vo = .... の式から Vo/Vi = f(Z1,Z2,Z3,Z4,Z5, G) の式を導きます。
PythonSf ワンライナー
ts(); I2,Im,Ig,Vi,Vm,Vo,V2,Z1,Z2,Z5,Z4,Z3,G = ts.symbols('I2,Im,Ig,Vi,Vm,Vo,V2,Z1,Z2,Z5,Z4,Z3,G'); ts.solve([ts.Eq(Im + (1+1/G) Vo/Z5), ts.Eq(1/Z3 (V2-Vo) - I2), ts.Eq(1/Z4 (V2-Vm) - Im),ts.Eq(V2 - Z2 Ig),ts.Eq(-Vi +V2 + Z1 I2 + Z1 Im + Z1 Ig),ts.Eq(V2+1/G Vo - Im Z4)], [I2,Im,Ig,Vo,Vm,V2])
===============================
{I2: Vi*Z2*(G*Z4 + G*Z5 + Z4 + Z5)/(G*Z1*Z2*Z3 + G*Z1*Z2*Z4 + G*Z1*Z2*Z5 + G*Z1*Z3*Z4 + G*Z2*Z3*Z4 + Z1*Z2*Z3 + Z1*Z2*Z4 + Z1*Z2*Z5 + Z1*Z3*Z4 + Z1*Z3*Z5 + Z2*Z3*Z4 + Z2*Z3*Z5), Im: Vi*Z2*Z3*(G + 1)/(G*Z1*Z2*Z3 + G*Z1*Z2*Z4 + G*Z1*Z2*Z5 + G*Z1*Z3*Z4 + G*Z2*Z3*Z4 + Z1*Z2*Z3 + Z1*Z2*Z4 + Z1*Z2*Z5 + Z1*Z3*Z4 + Z1*Z3*Z5 + Z2*Z3*Z4 + Z2*Z3*Z5), Vo: G*Vi*Z2*Z3*Z5/(-G*Z1*Z2*Z3 - G*Z1*Z2*Z4 - G*Z1*Z2*Z5 - G*Z1*Z3*Z4 - G*Z2*Z3*Z4 - Z1*Z2*Z3 - Z1*Z2*Z4 - Z1*Z2*Z5 - Z1*Z3*Z4 - Z1*Z3*Z5 - Z2*Z3*Z4 - Z2*Z3*Z5), Ig: Vi*Z3*(G*Z4 + Z4 + Z5)/(G*Z1*Z2*Z3 + G*Z1*Z2*Z4 + G*Z1*Z2*Z5 + G*Z1*Z3*Z4 + G*Z2*Z3*Z4 + Z1*Z2*Z3 + Z1*Z2*Z4 + Z1*Z2*Z5 + Z1*Z3*Z4 + Z1*Z3*Z5 + Z2*Z3*Z4 + Z2*Z3*Z5), V2: Vi*Z2*Z3*(G*Z4 + Z4 + Z5)/(G*Z1*Z2*Z3 + G*Z1*Z2*Z4 + G*Z1*Z2*Z5 + G*Z1*Z3*Z4 + G*Z2*Z3*Z4 + Z1*Z2*Z3 + Z1*Z2*Z4 + Z1*Z2*Z5 + Z1*Z3*Z4 + Z1*Z3*Z5 + Z2*Z3*Z4 + Z2*Z3*Z5), Vm: Vi*Z2*Z3*Z5/(G*Z1*Z2*Z3 + G*Z1*Z2*Z4 + G*Z1*Z2*Z5 + G*Z1*Z3*Z4 + G*Z2*Z3*Z4 + Z1*Z2*Z3 + Z1*Z2*Z4 + Z1*Z2*Z5 + Z1*Z3*Z4 + Z1*Z3*Z5 + Z2*Z3*Z4 + Z2*Z3*Z5)}
# Vo = .... の式
Vo= G*Vi*Z2*Z3*Z5/(-G*Z1*Z2*Z3 - G*Z1*Z2*Z4 - G*Z1*Z2*Z5 - G*Z1*Z3*Z4 - G*Z2*Z3*Z4 - Z1*Z2*Z3 - Z1*Z2*Z4 - Z1*Z2*Z5 - Z1*Z3*Z4 - Z1*Z3*Z5 - Z2*Z3*Z4 - Z2*Z3*Z5)
# Vo/Vi = f(Z1,Z2,Z3,Z4,Z5, G) の式
Vo/Vi= Z2 Z3 Z5/(-Z1 Z2 Z3 - Z1 Z2 Z4 - Z1 Z2 Z5 - Z1 Z3 Z4 - Z2 Z3 Z4 -(Z1 Z2 Z3 + Z1 Z2 Z4 + Z1 Z2 Z5 + Z1 Z3 Z4 + Z1 Z3 Z5 + Z2 Z3 Z4 +
Z2 Z3 Z5)/G)
--------------------------------------------------- (7)
上の 7 式なんて、手計算では絶対に計算しきれないと思います。途中で誤りが入り込んで計算が収束しないでしょう。sympy は凄いと思います。そして sympy で Python プログラム・コードを書くとしても、普通のエンジニアはデバッグ途中でギブ・アップすると思います。でもワン・ライナーであれこれ試せる PythonSf ならば、この程度のトポロジーの回路でも扱えます。ここらが限度の気もしますが、通常の回路設計ならば これで十分でしょう。各 Z ブロックは単一素子に限らなくて、任意の L C R の組み合わせでもかまわないのですから。
上で求めた Vo/Vi の式を下の多重帰還型バンドパスフィルタ回路に適用してみましょう。
┌──────┬──────┐
│Z3 │Z5 Vo │
─┴─1000p ≧220k │
─┬─ ≦ │
↑│I2 → │ │
Ii Z1 │V2 Z4 Im │ │
───MWMW──┼──┤├──┴─◆- │
Vi 22k │ 1000p Vm │ G>──┴───
≧Z2 ┌─◇+
≦1k │
│ │
≡ ≡
理想オペアンプでは次のような伝達関数・Bode 線図になります。
PythonSf ワンライナー
# 伝達関数
Z1,Z2,Z3,Z4,Z5 = 22kΩ`, 1kΩ`, 1/(1000pF` `s), 1/(1000pF` `s),220kΩ`; trf=Z2 Z3 Z5/(-Z1 Z2 Z3 - Z1 Z2 Z4 - Z1 Z2 Z5 - Z1 Z3 Z4 - Z2 Z3 Z4); trf
===============================
-4.545e+04 s
----------------------
2
s + 9091 s + 4.752e+09
PythonSf ワンライナー
# Bode 線図
Z1,Z2,Z3,Z4,Z5 = 22kΩ`, 1kΩ`, 1/(1000pF` `s), 1/(1000pF` `s),220kΩ`; trf=Z2 Z3 Z5/(-Z1 Z2 Z3 - Z1 Z2 Z4 - Z1 Z2 Z5 - Z1 Z3 Z4 - Z2 Z3 Z4); trf.plotBode(1k` Hz`,100k` Hz`)
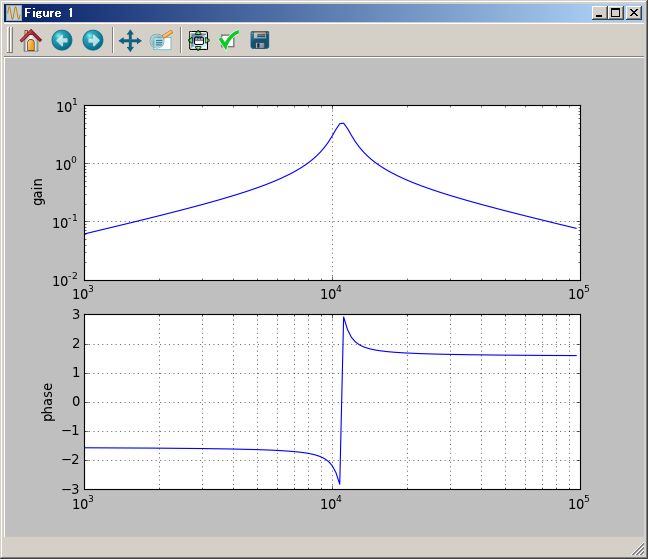
この伝達関数の極は次の PythonSf 式で求められます。
PythonSf ワンライナー
Z1,Z2,Z3,Z4,Z5 = 22kΩ`, 1kΩ`, 1/(1000pF` `s), 1/(1000pF` `s),220kΩ`; trf=Z2 Z3 Z5/(-Z1 Z2 Z3 - Z1 Z2 Z4 - Z1 Z2 Z5 - Z1 Z3 Z4 - Z2 Z3 Z4); trf.m_plDenom.roots
===============================
[-4545.45454545+68785.20886555j -4545.45454545-68785.20886555j]
uA741 オペアンプでは次のような伝達関数・Bode 線図になります。中心周波数が理想オペアンプのときより数 kHz 低くなります。
PythonSf ワンライナー
G=:uA741; Z1,Z2,Z3,Z4,Z5 = 22kΩ`, 1kΩ`, 1/(1000pF` `s), 1/(1000pF` `s),220kΩ`; trf=Z2 Z3 Z5/(-Z1 Z2 Z3 - Z1 Z2 Z4 - Z1 Z2 Z5 - Z1 Z3 Z4 - Z2 Z3 Z4 -(Z1 Z2 Z3 + Z1 Z2 Z4 + Z1 Z2 Z5 + Z1 Z3 Z4 + Z1 Z3 Z5 + Z2 Z3 Z4 + Z2 Z3 Z5)/G); trf
===============================
-2.856e+11 s
----------------------------------------
3 2
s + 7.338e+06 s + 6.214e+10 s + 2.986e+16
PythonSf ワンライナー
G=:uA741; Z1,Z2,Z3,Z4,Z5 = 22kΩ`, 1kΩ`, 1/(1000pF` `s), 1/(1000pF` `s),220kΩ`; trf=Z2 Z3 Z5/(-Z1 Z2 Z3 - Z1 Z2 Z4 - Z1 Z2 Z5 - Z1 Z3 Z4 - Z2 Z3 Z4 -(Z1 Z2 Z3 + Z1 Z2 Z4 + Z1 Z2 Z5 + Z1 Z3 Z4 + Z1 Z3 Z5 + Z2 Z3 Z4 + Z2 Z3 Z5)/G); trf.plotBode(1k` Hz`,100k` Hz`)
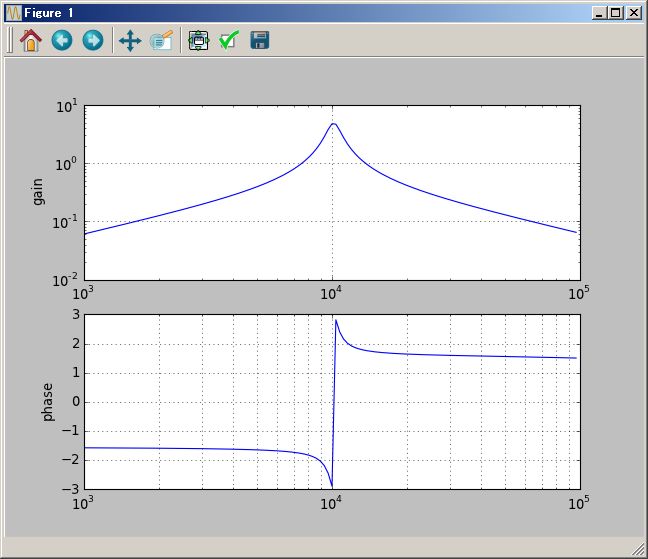
流石に複雑なトポロジーの回路で部品数も多い分、先の微分・積分回路によるバンド・パスのときより急峻な選択特性になっています。
この伝達関数の極は次の PythonSf 式で求められます。
PythonSf ワンライナー
G=:uA741; Z1,Z2,Z3,Z4,Z5 = 22kΩ`, 1kΩ`, 1/(1000pF` `s), 1/(1000pF` `s),220kΩ`; trf=Z2 Z3 Z5/(-Z1 Z2 Z3 - Z1 Z2 Z4 - Z1 Z2 Z5 - Z1 Z3 Z4 - Z2 Z3 Z4 -(Z1 Z2 Z3 + Z1 Z2 Z4 + Z1 Z2 Z5 + Z1 Z3 Z4 + Z1 Z3 Z5 + Z2 Z3 Z4 + Z2 Z3 Z5)/G); trf.m_plDenom.roots
===============================
[ -7.33006081e+06 +0.j -3.96063749e+03+63701.29330301j
-3.96063749e+03-63701.29330301j]
部品定数を変化させ根軌跡を描くことで、共振特性も検討できそうです。周波数選択特性も設計できそうです。
PythonSf 記述は数学記述に近いので、数学的な対象の説明では、自然言語による説明より PythonSf コードの方が解り易いことが多くあります。Fractal 図形について、その様子を見てみましょう。
なお、ここでは one-liner ではなく、ブロック・コードのほうが多用されます。One-liner にして再利用する意味は殆ど無いからです。ならば可読性を優先すべきだからです。
コッホ曲線を PythonSf で描きます。Wiki などにも Koch 曲線の説明があるのですが、下の 複素数を使ったコードのほうが解りやすいと思います。
PythonSf ブロック
# Koch 曲線
//@@
θ=exp(`i pi/3)
def f(lst,count=10):
if count<0:
return lst
rtn=[]
for k in range(len(lst)-1):
sg = (lst[k+1]-lst[k])/3
rtn += [lst[k], lst[k]+sg, lst[k]+sg+θ sg, lst[k]+sg 2]
rtn += [lst[-1] ]
return f(rtn, count-1)
plotTrajectory([ (x.real, x.imag) for x in f([0,1], 5)])
//@@@
上のコードの肝は、下の二行です。
sg = (lst[k+1]-lst[k])/3
rtn += [lst[k], lst[k]+sg, lst[k]+sg+θ sg, lst[k]+sg 2]
Koch 曲線を lst に平面位置:複素数値を順番に並べることで表現します。その部分セグメント:直線:lst[k+1]-lst[k] の 1/3 の線分 sg を作ります。sg ができたら、θ sg によって左方向に 60度回転させた線分を作れます。そして [lst[k], lst[k]+sg, lst[k]+sg+θ sg, lst[k]+sg 2] によって元の線分をもう一段階細かく折り曲げた四つの繋がった線分を作ります。
下は [0,1,0.5-`i, 0] の三角形の線分から Koch 曲線を作ることで、雪の結晶のような Koch 曲線にしています。
PythonSf ブロック
# 星型の Koch 曲線
//@@
θ=exp(`i pi/3)
def f(lst,count=10):
if count<0:
return lst
rtn=[]
for k in range(len(lst)-1):
sg = (lst[k+1]-lst[k])/3
rtn += [lst[k], lst[k]+sg, lst[k]+sg+θ sg, lst[k]+sg 2]
rtn += [lst[-1] ]
return f(rtn, count-1)
plotTrajectory([ (x.real, x.imag) for x in f([0,1,0.5-`i, 0], 5)])
//@@@
平面を埋め尽くす一次元の線として Hirbert Curve が有名です。でもWikiや WolframMathWorld などの説明を読んでも、どうやって描いていくのか簡単には理解できません。下の PythonSf ブロック・コードなら Hilbert Curve を作るアルゴリズムが良くわかると思います。いかがでしょうか?
PythonSf ブロック
//@@
N=3
# seed trajectory: matrix of position data
mt=~[(1/4,3/4),(1/4,1/4),(3/4,1/4),(3/4,3/4)]
mtL = ~[[ 0,1], # rotate pi/2 left
[-1,0]]
mtS = ~[[ 0,1], # symmetric conversion for x==y axis
[ 1,0]]
for _ in range(N):
mt=~[list((mt mtL)[::-1] +~[1,1])
+ list(mt)
+ list(mt+~[1,0])
+ list(mt mtS + ~[1,1])
]/2
plotTrajectory(mt)
//@@@
上のコードの肝は mt mtL と mt mtS の行列積です。mt は N x 2 行列であり N この平面位置ベクトルを保持しています。これに右から mtL:( pi/2 だけ回転させる) 変換と mtS:(x==y の直線に対称な位置に鏡影変換する行列を掛けることで位置ベクトルの羅列データ mt を変換しています。
標準配布の PythonSf の sfCrrntIni.py ファイルには wav ファイルを読み書きする readWv(..)/writeWv(..) 関数を書いてあります。readWv(..) 関数は wav ファイルのデータをベクトル・データに変換します。writeWv(..) 関数はベクトル・データのデータを wav ファイルに変換します。ベクトル・データであれば、PythonSf で自由に操作できます。
これを使って PythonSf one-liner による楽器音の合成や英語音声の解析を行います。
この小さな readWv(..)/wirteWv(..) カスタマイズ関数の導入だけで、PythonSf's one-liner による音声処理が可能になることを見てやってください。
pythonsf ブロック
//@@
f0=220Hz` # key 音
SR=44100Hz` # sampling rate
z_=1/`s # z^-1: z 変換記号
seed(0) # random の種
pluckedNoise=rand(SR//f0)-0.5 # 弦を引っ掛けるノイズ
F=0.996/2 (1+z_) # 減衰フィルタ 1
G=1/(1-F z_^(SR//f0)) # 減衰フィルタ 2: f0 での振動も生成する
# 伝達関数 G に pluked noise を与えたときの応答ベクトル data を作る
data=G.getDgRspns(np.r_[pluckedNoise, [0]*(SR-SR//f0)])
# 最大値を 2^15 に規格化する
data=2^15/max(abs(data))
# 規格化されたベクトル data をカレント・ディレクトリの temp.wav ファイルとして書き込む
writeWv(data, 'temp',(1, 2, SR, 32400, 'NONE', 'not compressed'))
//@@@
PythonSf ワンライナー
f0,SR,z_=220Hz`, 44100Hz`, 1/`s; seed(0);F=0.996/2 (1+z_); G=1/(1-F z_^(SR//f0)); data=G.getDgRspns(np.r_[rand(SR//f0)-0.5, [0]*(SR-SR//f0)]); data*=2^15/max(abs(data)); writeWv(data, 'temp',(1, 2, SR, 32400, 'NONE', 'not compressed'))
下のようにフィルタを追加して高周波を落としてやるとナイロン弦でのような音になります。
PythonSf ワンライナー
f0,SR,z_=220Hz`, 44100Hz`, 1/`s; seed(0); sy();y=sg.lfilter([0.1]*10,[1,1.0], rand(SR//f0)-0.5);F=0.996/4 (1+z_+z_^2+z_^3); G=1/(1-F z_^(SR//f0)); data=G.getDgRspns(np.r_[y, [0]*(SR-SR//f0)]); data=2^15/max(abs(data)) data; writeWv(data, 'temp',(1, 2, SR, 32400, 'NONE', 'not compressed'))
SciPy の signal sub package には、signal processing のための様々な関数群が用意されています。原理的には如何様なギター音でも合成できます。結構遊べます。
下のように love_rub.wav は 27545 点のデータからなり、1.728125 秒の長さの音声です。
PythonSf ワンライナーたち
readWv('love_rub').shape
==============================
(27545,)
ts(); 27645.0/(16 k` Hz`)
===============================
1.7278125*s`
WaveSurfer というソフトを使って、その波形とスペクトログラムの時間変化を下のように可視化できます。
日本人が L/R の区別をできないのは、日本語でのラ行の音に置き換えて聞いてしまうからです。love も rub も「ラブ」聞いてしまうからです。PythonSf を使って子音 L や R だけを取り出して実際に聞いてみましょう。
L の音は、love_ruv.wav ファイルで 0.358s -- 0.490s の範囲にあります。この時間幅をインデックスで表現すると、5707 -- 7011 の範囲です。下の計算で分かります。
PythonSf ワンライナーたち
# L の音の範囲のインデックスを計算する
27545 0.358s`/(1.7278125*s`)
===============================
5707.28015916
27545 0.490s`/(1.7278125*s`)
===============================
7811.64044131
7800-5700
===============================
2100
この L 子音の部分だけを抜き出して、デフォルトの _tmp.wav ファイに書き出します。ただし音声データを急激に 0 にするとプチ・ノイズになるので、最後の 200 点の音は直線状に絞って消します。したの arsq(1,200,-1/200) の部分が、それを行います。readWv(..) が「Numpy の ndarray データを返すこと」と「ndarray と list の積は要素ごとを掛け合わした ndarray でーたになること」を利用しています。
PythonSf ワンライナー
# love_rub.wav から子音 L の部分を抜き出して _tmp.wav ファイルに保存する。
vct=readWv('love_rub')[5700:7800]; writeWv(vct ( (1,)*1900+arsq(1,200,-1/200)) )
===============================
None
このようにして抜き出した子音 L の音:_tmp.wav を御自分の耳で是非とも聞いてください。日本語でのラ行の音とは異なることが分かると思います。この子音 L の部分だけ(母音とは独立させて)聞き取れるようになると L/R の誤認識を改善できます。
でもまだ この子音:L には余分なノイズに近い音が混じっています。私が L の音だと思っているのとは少し違いがあります。その L の音を抜き出すため、フーリエ変換を使います。
PythonSf ワンライナー
# 子音 L のフーリエ変換
vc=readWv('_tmp'); plotGr( abs( fftshift( fft(vc) ) ) )
上のグラフでフーリエ変換の絶対値のグラフは左右対称です。画面で左右対称になっていないのは、2100 点のデータをコンピュータ画面上で表示するときに歯抜けが発生するからです。歯抜けが左右対称には起きないためです。1000 点のデータ:±4kHz 弱の領域に限ると、下のように左右対称になります。
PythonSf ワンライナー
# 子音 L のフーリエ変換結果を中心部分 1000 点に限定してグラフ化する
vc=readWv('_tmp'); plotGr( abs( fftshift( fft(vc) ) )[2100/2-550: 2100/2+550] )
PythonSf ワンライナーたち
# 16kHz サンプリングの fft データから 220 点のデータを取り出したときの周波数
16k` Hz` 220/2100
===============================
1676.19047619
# 子音 L の音を±1.6kHz に限定した _tmp.wav ファイルを作る
vc=readWv('_tmp'); v=fft(vc); v[220:-220]=0; writeWv( ifft(v).real )
上のようにして作った _tmp.wav ファイルの音を自分の耳で聞いて見てください。love の音から、この部分の音に集中して聞き取るようにすることで love の英語の l が、日本語のラブとは違った音として聞き取れるようになってきます。
Diadic product を使って (E-2n2^n2) (E-2nm^nm) と回転行列を表せます。この式では二つの単位ベクトル n1, n2 により回転が定められています。nm は n1 と n2 の中央の単位ベクトルです。E は単位行列です。具体的に n1:[0,0,1] から n2:[0.29597008,-0.07621294, 0.95215193] への回転行列が下の PythonSf 式で計算されます。
PythonSf ワンライナー
n2,n1=~[0.29597008,-0.07621294, 0.95215193],[0,0,1]; N=3; E=kzrs(N,N)^0; nm=normalize(n1+n2); (E-2n2^n2) (E-2nm^nm)
===============================
[[ 0.95512732 0.01155481 0.29597008]
[ 0.01155481 0.99702461 -0.07621294]
[-0.29597008 0.07621294 0.95215193]]
---- ClTensor ----
回転軸単位ベクトル n の周りに θ 回転させる下の三次元行列の公式もあります。
三次元軸回転行列
[[ n[0]n[0] (1-cos(θ))+cos(θ), n[0]n[1] (1-cos(θ))-n[2]sin(θ), n[0]n[2] (1-cos(θ))+n[1]sin(θ)],
[ n[1]n[0] (1-cos(θ))+n[2]sin(θ), n[1]n[1] (1-cos(θ))+cos(θ), n[1]n[2] (1-cos(θ))-n[0]sin(θ)],
[ n[2]n[0] (1-cos(θ))-n[1]sin(θ), n[1]n[2] (1-cos(θ))+n[0]sin(θ), n[2]n[2] (1-cos(θ))+cos(θ)]]
回転軸 [1,2,3] の周りに pi/6 だけ回転させる行列は下の PythonSf 式で計算できます。
PythonSf ワンライナー
//@@
θ=pi/6
n = normalize([1,2,3])
mt=~[
[ n[0]n[0] (1-cos(θ))+cos(θ), n[0]n[1] (1-cos(θ))-n[2]sin(θ), n[0]n[2] (1-cos(θ))+n[1]sin(θ)],
[ n[1]n[0] (1-cos(θ))+n[2]sin(θ), n[1]n[1] (1-cos(θ))+cos(θ), n[1]n[2] (1-cos(θ))-n[0]sin(θ)],
[ n[2]n[0] (1-cos(θ))-n[1]sin(θ), n[1]n[2] (1-cos(θ))+n[0]sin(θ), n[2]n[2] (1-cos(θ))+cos(θ)]]
print mt
//@@@
[[ 0.87559502 -0.38175263 0.29597008]
[ 0.42003109 0.90430386 -0.07621294]
[-0.2385524 0.19104831 0.95215193]]
---- ClTensor ----
最初の diadic による回転での n1:[0.29597008,-0.07621294, 0.95215193] ベクトルは、上の回転行列の最後の列、すなわち [0,0,1] ベクトルを pi/6 回転させたベクトルの値でした。
ただし二つの回転行列が [0,0,1] を[0.29597008,-0.07621294, 0.95215193] に移す点では同じですが、両者の回転軸は異なります。ですから二つの行列は一致していません。
四元数を使っても、[1,2,3] ベクトルを回転軸とする回転を計算できます。[1,0,0],[0,1,0],[0,0,1] の回転は下のように計算できます。
PythonSf ワンライナー
θ=pi/6; voc=Oc(np.r_[cos(θ/2),normalize([1,2,3]) sin(θ/2)]); voc Oc(0,0,0,1) voc.conj()
===============================
Oc(0.0, 0.29597008395861607, -0.07621293686382874, 0.9521519299230139)
θ=pi/6; voc=Oc(np.r_[cos(θ/2),normalize([1,2,3]) sin(θ/2)]); voc Oc(0,0,1,0) voc.conj()
===============================
Oc(-8.6736173798840355e-18, -0.38175263483784205, 0.90430385984602779, 0.1910483050485956)
θ=pi/6; voc=Oc(np.r_[cos(θ/2),normalize([1,2,3]) sin(θ/2)]); voc Oc(0,1,0,0) voc.conj()
===============================
Oc(0.0, 0.87559501779983595, 0.42003109089943103, -0.23855239986623264)
回転行列の記述は (E-2n1^n1) (E-2nm^nm) の方が単純です。それ以上に (E-2n1^n1) (E-2nm^nm) は任意次元の回転にも適用できます。少しの修正で Minkowski 空間での回転:Lorentz 変換にも適用できます。一方で回転軸周りの回転行列や四元数による回転は三次元空間にしか適用できません。元々回転軸の概念が使えるのは三次元空間だけの特殊事情によるものです。( たとえば四次元空間での回転では、回転軸が二本になります。二次元空間では回転軸は存在しません。スカラーの回転角しか存在しません。)
もっと (E-2n1^n1) (E-2nm^nm) 公式を活用しましょう。
ここでは (E-2n1^n1) (E-2nm^nm) が回転行列になる理由を検討します。(E-2n^n) が鏡影変換であり、E-2nm^nm が n1 方向のベクトルを -n2 方向に変換することで回転が実現されます。
単位ベクトル n に対し n^n 行列は n が張る一次空間への射影変換になっています。下の Dirac 流の記法に変形してやれば射影変換であることが見えてくると思います。(下の変形では納得できないかたは、別途 御自分で数値実験を行ってみてください。)
式の変形
n^n v == |n><n| v == |n> <n|v>
さて、n1 から n2 への回転変換のために、その中央の単位ベクトル nm = normalize(n1+n2) を作ります。その nm に対して n1 の反射:reflection: (E-2nm^nm) n1 は -n2 になっています。下のように数値実験で確認できます。
PythonSf ワンライナー
seed(0);nmlz=normalize; N=4; n1,n2=nmlz(randn(N)),nmlz(randn(N));E=kzrs(N,N)^0; nm=nmlz(n1+n2); (E-2nm^nm) n1, -n2
===============================
(ClTensor([-0.8060292 , 0.42178851, -0.41005367, 0.06532506]),
ClTensor([-0.8060292 , 0.42178851, -0.41005367, 0.06532506]))
これを二次元の場合に視覚化すると、下のようになります。
PythonSf ワンライナー
pt,nmlz=plotTrajectory,normalize; seed(0);N=2; n1,n2=nmlz(randn(N)),nmlz(randn(N)); E=kzrs(N,N)^0; nm=nmlz(n1+n2); M= (E-2nm^nm); O=kzrs(N); pt([O,n1]); pt([O,nm],green); pt([O,M n1],red); pt([O,n2],orange)
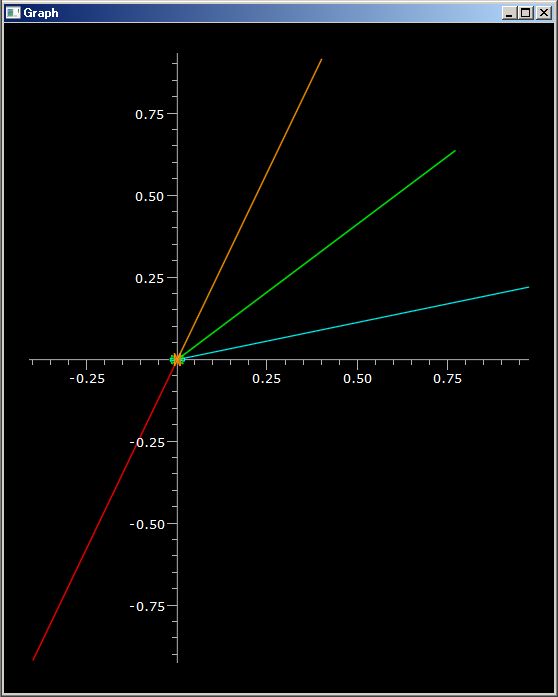
n1:cyan と n2:orange に対して nm:green を作り、(E-2nm^nm) n1:red を作ると、それは n2 の向きだけが変わったベクトルになっています。
これを三次元の場合に可視化すると、下のようになります。
PythonSf ワンライナー
pt,nmlz=plotTrajectory,normalize; seed(0);N=3; n1,n2=nmlz(randn(N)),nmlz(randn(N)); E=kzrs(N,N)^0; nm=nmlz(n1+n2); M= (E-2nm^nm); O=kzrs(N); pt([O,n1]); pt([O,nm],green); pt([O,M n1],red); pt([O,n2],orange)
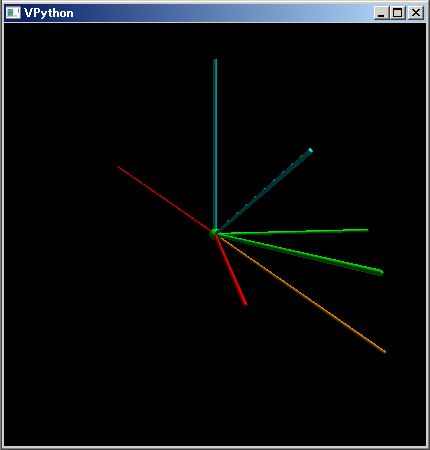
n1:cyan と n2:orange に対して nm:green を作り、(E-2nm^nm) n1:red を作ると、それは n2 の向きだけが変わったベクトルになっています。
n2 の向きだけが変わったベクトルが得られたら、それを (E-2n2^n2) で反射させてやれば、n2 になります。すなわち (E-2n2^n2) (E-2nm^nm) n1 == n2 になっています。 すなわち、n1 ベクトルを n2 ベクトルに変換する線形変換になっています。
PythonSf ワンライナー
seed(0);nmlz=normalize; N=4; n1,n2=nmlz(randn(N)),nmlz(randn(N));E=kzrs(N,N)^0; nm=nmlz(n1+n2); (E-2n2^n2) (E-2nm^nm) n1, n2
===============================
(ClTensor([ 0.8060292 , -0.42178851, 0.41005367, -0.06532506]),
ClTensor([ 0.8060292 , -0.42178851, 0.41005367, -0.06532506]))
diadic 回転行列は SO(N):N次特殊直行変換 であることを次の数値実験で確認します。
PythonSf ワンライナーたち
seed(0);nmlz=normalize; N=3; n1,n2=nmlz(randn(N)),nmlz(randn(N));E=kzrs(N,N)^0; nm=nmlz(n1+n2); M=(E-2n2^n2) (E-2nm^nm); M M.t
===============================
[[ 1.00000000e+00 -1.11022302e-16 2.22044605e-16]
[ -1.11022302e-16 1.00000000e+00 -5.55111512e-17]
[ 2.22044605e-16 -5.55111512e-17 1.00000000e+00]]
---- ClTensor ----
seed(0);nmlz=normalize; N=4; n1,n2=nmlz(randn(N)),nmlz(randn(N));E=kzrs(N,N)^0; nm=nmlz(n1+n2); M=(E-2n2^n2) (E-2nm^nm); M M.t
===============================
[[ 1.00000000e+00 -3.33066907e-16 2.49800181e-16 -1.66533454e-16]
[ -3.33066907e-16 1.00000000e+00 -1.11022302e-16 1.66533454e-16]
[ 2.49800181e-16 -1.11022302e-16 1.00000000e+00 -1.66533454e-16]
[ -1.66533454e-16 1.66533454e-16 -1.66533454e-16 1.00000000e+00]]
---- ClTensor ----
# 上の二つの計算結果を行列の pretty print で表示する
seed(0);nmlz=normalize; N=3; n1,n2=nmlz(randn(N)),nmlz(randn(N));E=kzrs(N,N)^0; nm=nmlz(n1+n2); M=(E-2n2^n2) (E-2nm^nm); pp(M M.t)
[[ 1, 0, 0]
,[ 0, 1, 0]
,[ 0, 0, 1]]
-------- pp --
===============================
None
seed(0);nmlz=normalize; N=4; n1,n2=nmlz(randn(N)),nmlz(randn(N));E=kzrs(N,N)^0; nm=nmlz(n1+n2); M=(E-2n2^n2) (E-2nm^nm); pp(M M.t)
[[ 1, 0, 0, 0]
,[ 0, 1, 0, 0]
,[ 0, 0, 1, 0]
,[ 0, 0, 0, 1]]
-------- pp --
===============================
None
# M * transpose(M) == 単位行列だから M は SO(N)
seed(0);nmlz=normalize; N=4; n1,n2=nmlz(randn(N)),nmlz(randn(N));E=kzrs(N,N)^0; nm=nmlz(n1+n2); M=(E-2n2^n2) (E-2nm^nm); (M M.t) ~== E
===============================
True
ここでは、diadic 回転行列の回転軸:固有値が 1 の固有ベクトルが n1,n2 に対して垂直であることを固有値と固有ベクトルを使って数値実験で確認します。
PythonSf ワンライナーたち
# 三次元 diadic 回転行列の固有値と固有ベクトル
seed(0);nmlz=normalize; N=3; n1,n2=nmlz(randn(N)),nmlz(randn(N));E=kzrs(N,N)^0; nm=nmlz(n1+n2); eig((E-2n2^n2) (E-2nm^nm))
===============================
(ClTensor([ 0.59170657+0.80615342j, 0.59170657-0.80615342j, 1.00000000+0.j ], dtype=complex),
ClTensor([[ 0.63669391+0.j , 0.63669391+0.j , -0.43501924+0.j ],
[ 0.26235734-0.36915858j, 0.26235734+0.36915858j, 0.76797210+0.j ],
[ 0.16059108+0.60309365j, 0.16059108-0.60309365j, 0.47008203+0.j ]], dtype=complex))
# 固有ベクトル:回転軸:[-0.43501924, 0.76797210, 0.47008203] は n1,n2 に垂直
seed(0);nmlz=normalize; N=3; n1,n2=nmlz(randn(N)),nmlz(randn(N)); vc=~[-0.43501924, 0.76797210, 0.47008203]; n1 vc, n2 vc
===============================
(-3.9705849719240405e-10, 1.7822789077914791e-09)
# 四次元 diadic 回転行列の固有値と固有ベクトル
seed(0);nmlz=normalize; N=4; n1,n2=nmlz(randn(N)),nmlz(randn(N));E=kzrs(N,N)^0; nm=nmlz(n1+n2); eig((E-2n2^n2) (E-2nm^nm))
===============================
(ClTensor([ 0.49580083+0.86843626j, 0.49580083-0.86843626j, 1.00000000+0.j, 1.00000000+0.j], dtype=complex),
ClTensor([[ 0.10451402-0.57920593j, 0.10451402+0.57920593j, 0.55425140+0.j, -0.21666328+0.j ],
[ 0.29858200+0.27703642j, 0.29858200-0.27703642j, 0.46641336+0.j, -0.80021953+0.j ],
[ 0.07487605-0.29626223j, 0.07487605+0.29626223j,-0.64744064+0.j, -0.32470320+0.j ],
[ 0.62794839+0.j , 0.62794839+0.j ,-0.23682182+0.j, 0.45527307+0.j ]], dtype=complex))
# 固有ベクトル:回転軸:[0.55425140,0.46641336,-0.64744064,-0.23682182] は n1,n2 に垂直
seed(0);nmlz=normalize; N=4; n1,n2=nmlz(randn(N)),nmlz(randn(N)); vc=~[0.55425140,0.46641336,-0.64744064,-0.23682182]; n1 vc, n2 vc
===============================
(-7.1461675466011343e-10, 3.2174553021846464e-09)
# 固有ベクトル:回転軸:[-0.21666328,-0.80021953,-0.32470320,0.45527307] は n1,n2 に垂直
seed(0);nmlz=normalize; N=4; n1,n2=nmlz(randn(N)),nmlz(randn(N)); vc=~[-0.21666328,-0.80021953,-0.32470320,0.45527307]; n1 vc, n2 vc
===============================
(-3.1670128464167391e-09, -1.8834036275006127e-09)
Minkowski での diadic 回転行列で空間回転:Lorentz boost 変換を記述します。ただし単位行列の norm が -1 になるので、符号が変わって diadic 回転行列は (E+2n2^n2) (E+2nm^nm) となります。(ただし Lorentz boost 変換がこのように表されるのであり、空間回転も含む一般の Lorentz 変換は、空間回転 (E-2m2^m2) (E-2mm^nm) の掛け算が入り込んできます。)
次のワンライナーで速度ベクトルに対する Lorentz boost 変換を求められます。
PythonSf ワンライナーたち
# 速度ベクトル [0.8, 0.1] に対する Lorentz boost 変換
mnl=λ v:`i v/sqrt(v v) ; n2,n1=mnl(~[0.8,0.1, `i]),~[0,0,`i]; nm=mnl(n1+n2); E=kzrs(3,3)^0; (E+2n2^n2) (E+2nm^nm)
===============================
[[ 1.67968838+0.j 0.08496105+0.j 0.00000000-1.35224681j]
[ 0.08496105+0.j 1.01062013+0.j 0.00000000-0.16903085j]
[ 0.00000000+1.35224681j 0.00000000+0.16903085j 1.69030851+0.j ]]
---- ClTensor ----
# Lorentz boost 変換の直交性
mnl=λ v:`i v/sqrt(v v) ; n2,n1=mnl(~[0.8,0.1, `i]),~[0,0,`i]; nm=mnl(n1+n2); E=kzrs(3,3)^0; M=(E+2n2^n2) (E+2nm^nm); M M.t
===============================
[[ 1.00000000e+00 +0.00000000e+00j -4.57966998e-16 +0.00000000e+00j 0.00000000e+00 -8.43769499e-15j]
[ -4.57966998e-16 +0.00000000e+00j 1.00000000e+00 +0.00000000e+00j 0.00000000e+00 -8.32667268e-16j]
[ 0.00000000e+00 -8.27810043e-15j 0.00000000e+00 -8.32667268e-16j 1.00000000e+00 +0.00000000e+00j]]
---- ClTensor ----
mnl=λ v:`i v/sqrt(v v) ; n2,n1=mnl(~[0.8,0.1, `i]),~[0,0,`i]; nm=mnl(n1+n2); E=kzrs(3,3)^0; M=(E+2n2^n2) (E+2nm^nm); pp(M M.t)
[[ 1, 0, 0]
,[ 0, 1, 0]
,[ 0, 0, 1]]
-------- pp --
===============================
None
# 速度ベクトル [0.8, 0.1,0.2] に対する Lorentz boost 変換
mnl=λ v:`i v/sqrt(v v) ; n2,n1=mnl(~[0.8,0.1,0.2, `i]),~[0,0,0,`i]; nm=mnl(n1+n2); E=kzrs(4,4)^0; (E+2n2^n2) (E+2nm^nm)
===============================
[[ 1.73836802+0.j 0.09229600+0.j 0.18459200+0.j 0.00000000-1.43684242j]
[ 0.09229600+0.j 1.01153700+0.j 0.02307400+0.j 0.00000000-0.1796053j ]
[ 0.18459200+0.j 0.02307400+0.j 1.04614800+0.j 0.00000000-0.3592106j ]
[ 0.00000000+1.43684242j 0.00000000+0.1796053j 0.00000000+0.3592106j
1.79605302+0.j ]]
---- ClTensor ----
mnl=λ v:`i v/sqrt(v v) ; n2,n1=mnl(~[0.8,0.1,0.2, `i]),~[0,0,0,`i]; nm=mnl(n1+n2); E=kzrs(4,4)^0; pp((E+2n2^n2) (E+2nm^nm))
[[ 1.73837, 0.092296, 0.184592, -1.43684j]
,[ 0.092296, 1.01154, 0.023074, -0.179605j]
,[ 0.184592, 0.023074, 1.04615, -0.359211j]
,[ 1.43684j, 0.179605j, 0.359211j, 1.79605]]
-------- pp --
===============================
None
# Lorentz boost 変換の直交性
mnl=λ v:`i v/sqrt(v v) ; n2,n1=mnl(~[0.8,0.1,0.2, `i]),~[0,0,0,`i]; nm=mnl(n1+n2); E=kzrs(4,4)^0; M=(E+2n2^n2) (E+2nm^nm); M M.t
===============================
[[ 1.00000000e+00 +0.00000000e+00j 8.55218674e-16 +0.00000000e+00j 2.24820162e-15 +0.00000000e+00j 0.00000000e+00 +7.99360578e-15j]
[ 8.55218674e-16 +0.00000000e+00j 1.00000000e+00 +0.00000000e+00j 2.63677968e-16 +0.00000000e+00j 0.00000000e+00 +9.43689571e-16j]
[ 2.24820162e-15 +0.00000000e+00j 2.63677968e-16 +0.00000000e+00j 1.00000000e+00 +0.00000000e+00j 0.00000000e+00 +2.55351296e-15j]
[ 0.00000000e+00 +8.09075029e-15j 0.00000000e+00 +9.61036806e-16j 0.00000000e+00 +2.60902411e-15j 1.00000000e+00 +0.00000000e+00j]]
---- ClTensor ----
mnl=λ v:`i v/sqrt(v v) ; n2,n1=mnl(~[0.8,0.1,0.2, `i]),~[0,0,0,`i]; nm=mnl(n1+n2); E=kzrs(4,4)^0; M=(E+2n2^n2) (E+2nm^nm); pp(M M.t)
[[ 1, 0, 0, 0]
,[ 0, 1, 0, 0]
,[ 0, 0, 1, 0]
,[ 0, 0, 0, 1]]
-------- pp --
===============================
None
ちなみに、この Lorentz boost 変換の回転軸は下のように求められます。3+1 次元では二つの回転軸が出てきます。
PythonSf ワンライナーたち
mnl=λ v:`i v/sqrt(v v) ; n2,n1=mnl(~[0.8,0.1, `i]),~[0,0,`i]; nm=mnl(n1+n2); E=kzrs(3,3)^0; M=(E+2n2^n2) (E+2nm^nm); eig(M)
===============================
(ClTensor([ 3.05307880+0.j, 0.32753822+0.j, 1.00000000+0.j], dtype=complex),
ClTensor([[ 0.00000000 -7.01646415e-01j, 0.00000000 +7.01646415e-01j, -0.12403473 +0.00000000e+00j],
[ 0.00000000 -8.77058019e-02j, 0.00000000 +8.77058019e-02j, 0.99227788 +0.00000000e+00j],
[ 0.70710678 +0.00000000e+00j, 0.70710678 +0.00000000e+00j, 0.00000000 -3.96028899e-17j]],
dtype=complex))
mnl=λ v:`i v/sqrt(v v) ; n2,n1=mnl(~[0.8,0.1,0.2, `i]),~[0,0,0,`i]; nm=mnl(n1+n2); E=kzrs(4,4)^0; M=(E+2n2^n2) (E+2nm^nm); eig(M)
===============================
(ClTensor([ 3.28796671+0.j, 0.30413933+0.j, 1.00000000+0.j, 1.00000000+0.j], dtype=complex),
ClTensor([[ 0.00000000 -6.81005225e-01j, 0.00000000 +6.81005225e-01j, -0.17983325 -0.00000000e+00j, -0.12615712 -0.00000000e+00j],
[ 0.00000000 -8.51256531e-02j, 0.00000000 +8.51256531e-02j, -0.37782401 -0.00000000e+00j, 0.99197263 +0.00000000e+00j],
[ 0.00000000 -1.70251306e-01j, 0.00000000 +1.70251306e-01j, 0.90824502 +0.00000000e+00j, 0.00864215 -0.00000000e+00j],
[ 0.70710678 +0.00000000e+00j, 0.70710678 +0.00000000e+00j, -0.00000000 -3.20682809e-16j, -0.00000000 -4.55432110e-16j]], dtype=complex))
この回転軸を上手く言葉で説明できないのですが、下の x 軸方向のみに動いているときの Lorentz 変換の回転軸を見てもらえれば、二つの回転軸の意味も分ってもらえると思います。
PythonSf ワンライナー
mnl=λ v:`i v/sqrt(v v) ; n2,n1=mnl(~[0.8,0.0,0.0, `i]),~[0,0,0,`i]; nm=mnl(n1+n2); E=kzrs(4,4)^0; M=(E+2n2^n2) (E+2nm^nm); eig(M)
===============================
(ClTensor([ 0.33333333+0.j, 3.00000000+0.j, 1.00000000+0.j, 1.00000000+0.j], dtype=complex),
ClTensor([[ 0.70710678+0.j , -0.00000000-0.70710678j, 0.00000000+0.j , 0.00000000+0.j ],
[-0.00000000-0.j , 0.00000000+0.j , 1.00000000+0.j , 0.00000000+0.j ],
[-0.00000000-0.j , 0.00000000+0.j , 0.00000000+0.j , 1.00000000+0.j ],
[-0.00000000-0.70710678j, 0.70710678+0.j , 0.00000000+0.j , 0.00000000+0.j ]], dtype=complex))
Diadic 回転行列を調べ始めたのは、与えられた速度ベクトルに対する Lorentz 変換を求める単純な式が欲しかったためでした。
Google 検索で やっと見つけたのがこの宇宙工学演習問題 にあった問題13の R1=U-2n1 n2,R2=U-2n2 n2, Q=R1 R2 の式でした。
一週間弱かかりましたが、この式だけから、上で論じたような考察を経て Lorentz 変換まで辿り着けました。この間は結構面白く色々と遊べました。
こんな検討・考察は PythonSf がなければ無理だと思います。Matlab や Mathematica では、こんなことはできないと思います。皆様はどう思われますでしょうか。
なお、Q = R1 R2 は R2 R1 の typo だと思います。R1 R2 のままだと n2 から n1 への回転になるからです。
また diadic tensor rotation などで検索したのですが、上の pdf の他には diadic 回転行列に触れている web page を見つけられませんでした。便利な diadic 回転行列が他に論じられないのが不思議です。四元数よりも diadic 回転行列のほうが便利なのに。
Diadic 回転行列が殆ど使われない理由を御存知の方がいたら、教えていただけますでしょうか。
自然単位系:suffix n、修正自然単位系:suffix k(自然単位系での単位電荷を素電荷に修正した単位系), Planck 単位系:suffix p、Stoney 単位系:suffix s の四つを PythonSf のカスタマイズ・ファイル sfCrrntIni.py に実装してみました。ここの wikipedia に従って実装しています。(修正自然単位系は素電荷を単位電荷とする PythonSf 独自の単位系であり、この wikipedia にも解説されていません。)
例えば、自然単位系:n、修正自然単位系:k, Planck 単位系:p、Stoney 単位系:s での単位長さ、単位質量、単位時間、単位電荷は SI 単位系では以下の値になります。
PythonSf ワンライナーたち
# 自然:n、修正自然:k, Planck :p、Stoney:s 単位系における単位長さの SI 単位系での値
tt(); toSI(mn`), toSI(mk`), toSI(mp`), toSI(ms`)
===============================
(1.97325397334585e-7*m`, 1.97325397334585e-7*m`, 1.61604781821404e-35*m`, 1.3805124167657e-36*m`)
# 自然:n、修正自然:k, Planck :p、Stoney:s 単位系における単位質量の SI 単位系での値
tt(); toSI(gn`), toSI(gk`), toSI(gp`), toSI(gs`)
===============================
(1.7826759031885e-36*kg`, 1.7826759031885e-36*kg`, 2.17671300905077e-8*kg`, 1.85946189392522e-9*kg`)
# 自然:n、修正自然:k, Planck :p、Stoney:s 単位系における単位時間の SI 単位系での値
tt(); toSI(sn`), toSI(sk`), toSI(sp`), toSI(ss`)
===============================
(6.58206676215268e-16*s`, 6.58206676215268e-16*s`, 5.39055528279515e-44*s`, 4.60489375208263e-45*s`)
# 自然:n、修正自然:k, Planck :p、Stoney:s 単位系における単位電荷の SI 単位系での値
tt(); toSI(Cn`), toSI(Ck`), toSI(Cp`), toSI(Cs`)
===============================
(5.29081721512368e-19*A`*s`, 1.6021892e-19*A`*s`, 5.29081721512368e-19*A`*s`, 1.6021892e-19*A`*s`)
# tt() を呼び出す前は mn`,mk`,gn`,gk`,sn`,sk`,Cn`,Ck` は単なる整数の 1
mn`,mk`,gn`,gk`,sn`,sk`,Cn`,Ck`
===============================
(1, 1, 1, 1, 1, 1, 1, 1)
# tt() を呼び出した後は mn`,mk`,gn`,gk`,sn`,sk`,Cn`,Ck` は SymPy ユニット・インスタンス
tt(); mn`,mk`,gn`,gk`,sn`,sk`,Cn`,Ck`
===============================
(mn`, mk`, gn`, gk`, sn`, sk`, Cn`, Ck`)
全ての単位系に共通な物理定数として、光速度、換算プランク定数:Dirac 定数、電子の電荷の三つを定義してあります。以下のように計算されます。
PythonSf ワンライナーたち
# 自然、修正自然、Planck、Stoney 単位系での光速度
tt(); cn`,ck`,cp`,cs`
===============================
(mn`/sn`, mk`/sk`, mp`/sp`, ms`/ss`)
# 自然、修正自然、Planck、Stoney 単位系での Dirac 定数
tt(); hn``,hk``,hp``,hs``
===============================
(gn`*mn`**2/sn`, gk`*mk`**2/sk`, gp`*mp`**2/sp`, 137.033824947109*gs`*ms`**2/ss`)
# 自然、修正自然、Planck、Stoney 単位系における電子の電荷
tt(); eQn`,eQk`,eQp`,eQs`
===============================
(0.302824523103951*Cn`, Ck`, 0.302824523103951*Cp`, Cs`)
修正自然単位系は、光速度の数分の一で動く電子を、 PythonSf を使った相対論的電磁気学の検討で扱うために導入しました。自然単位系では、単位電荷が素電荷:自然界に存在する最小電荷の 3.302 倍の値になっており、3.302 の不自然な係数を嫌って修正自然単位系を敢えて作りました。この修正自然単位系は、副次効果として SI 単位系に真空の誘電率・透磁率:e0,u0 が導入される理由も浮かびあがらせてくれます。このことは、最後の「SI単位系での理由」の節で論じます。
PythonSf ワンライナー
# 自然単位系では単位電荷は素電荷の 3.302 倍
tt(); Cn`/eQn` # eQn is the elementary charge
===============================
3.30224246619792
ここでは、単位電荷の定め方について検討します。
Planck 定数:h`` 、光速度定数:c` および、それと独立した値:例えば 1eV エネルギーや万有引力低数:gU` を元に単位長さ・単位質量・単位時間を定められます。この三つが与えられれば、単位力も決まります。
L,M,T 単位値より explicit に単位電荷を定めるために微細構造定数を使います。微細構造定数は無次元の物理定数であり、どんな単位系であっても 0.00729746834685501 の値をとります。
単位力から単位電荷を定める?単位電荷は、「単位距離だけ離した位置に置いた単位電荷どうしに単位力または単位力/(4π) が発生する」ことより、L,M,T 単位値が定まると単位電荷も定まってしまうように思えます。でも これは成り立たちません。クーロン力と電荷の物理次元は不定の関係にあります。
PythonSf ワンライナー
# 微細構造定数 α
α=;;ts(); eQ`^2/(4pi e0` h`` c`) J`/s`/W`
===============================
0.00729746834685501
一方で e0 h/2pi c は電荷の二乗の次元となる物理量です。自然単位系、Planck 単位系では e0`, h``, c` の数値が 1 となることより、e0` h`` c` は単位電荷の二乗となる物理量だとみなせます。
PythonSf ワンライナー
# e0 h/2pi c
ts(); e0` h`` c` W` s`/J`
===============================
2.79927468038491e-37*A`**2*s`**2
ならば微細構造定数の式を変形して、単位電荷 == e0` h`` c` == sqrt(eQ`^2/(4pi α))== eQ`/sqrt(4pi α)の式により、自然単位系・Planck 単位系での単位電荷を explicit に表せます。自然単位系・Planck 単位系どちらでも h`` c` の積は同じであるため、両方の単位電荷は同じになります。
PythonSf ワンライナー
# 単位電荷 == e0` h`` c` == eQ`/sqrt(4pi α)
tt(); eQ`/sqrt(4pi α`), toSI(Cn`), toSI(Cp`)
===============================
(5.29081721512368e-19*A`*s`, 5.29081721512368e-19*A`*s`, 5.29081721512368e-19*A`*s`)
修正自然単位系では素電荷を単位電荷とした代償として e0k` の値が 1 からずれてきます。
PythonSf ワンライナー
# e0 == eQ^2/(4pi α h/2pi c)
tt(); eQk`^2/(4pi α` hk`` ck`)
===============================
10.904805305561*Ck`**2*sk`**2/(gk`*mk`**3)
この 10.904805305561 の値は (自然単位系の単位電荷/修正自然単位系の単位電荷)^2 です。
PythonSf ワンライナー
# (自然単位系の単位電荷/修正自然単位系の単位電荷)^2
tt(); toSI(Cn`)^2/toSI(Ck`)^2
===============================
10.9048053055610
逆に言えば、h`` c` の値が 1 となる 距離:L・質量:M・時間:T の基本単位のとり方には、まだ自由度 2 の不定性が残っているが、h`` c` が 1 となるときの単位電荷は素電荷の 3.302 倍に限定されてしまいます。電子の電荷を単位電荷とし h`` c` が 1 となる単位系を作ろうとすると e0 が 1 でなくなってしまいます。
これらのことから分りにくい微細構造定数の物理的意味も見えてくると思うのですが如何でしょうか。
自然単位系の機能実装は、カレント・ディレクトリに置かれる sfCrrntIniRelativity.py と sfCrrntIniOpRelativity.py ファイルに実装してあります。そのソース・コードは、以下のようになっています。
PythonSf ワンライナー
import sfCrrntIni as md; np.source(md)
In file: sfCrrntIni.py
# coding=shift_jis
"""'
We implemented Natural, modified Natural, Planck and Stoney unit system
according to wikipedia:http://en.wikipedia.org/wiki/Natural_units.
We implemented Natural/Modified Natural unit systems to deal with relativistic electro-magnetism. Because it is too complex to deal with relativistic electro-magnetism in SI unit system. We implemented Planck/Stoney unit system to clearify relations between unit systems.
'"""
import sympy as sym
import pysf.symIntf as ut
import pysf.customize as ct
import pysf.sfFnctns as sf
__dctGlb = sf.__getDctGlobals()
_unitConstantGlb=None
class ClLllUnit(ut.Unit):
def __init__(self, name, abbrev):
# ut.Unit.__new__(..) expect only 2 argments:name, abbrev, so we can't
# pass _unitConstantGlb value through __init__(..) parameters.
self.m_toSI = _unitConstantGlb
k_mn_bq____ = k_gn_bq____ =k_sn_bq____ =k_eVn_bq____ =k_Cn_bq____ =k_Nn_bq____ =k_Jn_bq____ =k_Vn_bq____ =k_dVn_bq____ =k_e0n_bq____ =k_u0n_bq____ =k_hn_bq__bq____ = 1
k__sAlpha_n_bq____ = 0.0917026917931351
k_mk_bq____ = k_gk_bq____ =k_sk_bq____ =k_eVk_bq____ =k_Ck_bq____ =k_Nk_bq____ =k_Jk_bq____ =k_Vk_bq____ =k_dVk_bq____ =k_eQk_bq____ =k_hk_bq__bq____ = k__sAlpha_k_bq____ = 1
k_e0k_bq____ = 10.904805305561
k_u0k_bq____ = 0.0917026917931351
k_mLn_bq____ = k_mLk_bq____ = 1j
def tt():
global _unitConstantGlb
def toSI(ag):
ag = 1.0 * ag
at = 1
if ag.args == ():
return ag
for elm in ag.args:
if isinstance(elm,(sym.Integer, sym.Float)):
at *= elm
elif elm.is_Pow:
if isinstance(elm.args[0], ClLllUnit):
at *= elm.args[0].m_toSI ** elm.args[1]
else:
at *= elm.args[0] ** elm.args[1]
elif isinstance(elm, ClLllUnit):
at *= elm.m_toSI
else:
at *= elm
return at
ct.ts()
__alpha = __dctGlb['k_eQ_bq____'] **2/(
4*sf.pi
*__dctGlb['k_e0_bq____']
* __dctGlb['k_h_bq__bq____']
* __dctGlb['k_c_bq____']
) * __dctGlb['k_J_bq____'] / __dctGlb['k_s_bq____'] / __dctGlb['k_W_bq____']
k__sAlpha__bq____ = __alpha
# *****************************************************************************
# **** define Natural units in particle physics h``==c`==kB`== eQ` V` == 1 ****
# *****************************************************************************
__eV = __dctGlb['k_eQ_bq____'] * __dctGlb['k_V_bq____'] *(
__dctGlb['k_J_bq____']/__dctGlb['k_s_bq____']/__dctGlb['k_W_bq____'])
# define length:mn`
_unitConstantGlb = __dctGlb['k_c_bq____'] * __dctGlb['k_h_bq__bq____']/__eV
k_mn_bq____ = ClLllUnit('meter_n','mn`')
# define mass:gn`
_unitConstantGlb = __eV/__dctGlb['k_c_bq____'] **2
k_gn_bq____ = ClLllUnit('gram_n','gn`')
# define time:sn`
_unitConstantGlb = __dctGlb['k_h_bq__bq____']/__eV
k_sn_bq____ = ClLllUnit('second_n','sn`')
# define electron volt :eVn`
_unitConstantGlb = __eV
k_eVn_bq____ = ClLllUnit('electronVolt_n','eVn`')
# define Lorentz Heaviside electric charge:Cn`
_unitConstantGlb = __dctGlb['k_eQ_bq____']/sf.sqrt(4*sf.pi*__alpha)
k_Cn_bq____ = ClLllUnit('Coulomb_n','Cn`')
# deived units
# force Newton
k_Nn_bq____ = 1* k_gn_bq____ * k_mn_bq____ * k_sn_bq____ **-2
# energy Joule
k_Jn_bq____ = 1* k_gn_bq____ * k_mn_bq____**2 * k_sn_bq____ **-2
# Voltage
k_Vn_bq____ = 1* k_gn_bq____ * k_mn_bq____ **2 * k_sn_bq____ **-2 * k_Cn_bq____**-1
k_dVn_bq____ = 1* k_mn_bq____ **-1 * k_Cn_bq____
# e0` like constant
k_e0n_bq____ = 1* k_Vn_bq____**-1 * k_Cn_bq____* k_mn_bq____**-1
# mLght:meter of light:unit length of light --- pure imaginary number
k_mLn_bq____ = sym.I * k_mn_bq____
# physical constant
# light velocity
k_cn_bq____ = 1* k_mn_bq____ / k_sn_bq____
# h`/(2pi)
k_hn_bq__bq____ = 1* k_gn_bq____ * k_mn_bq____ ** 2/ k_sn_bq____
# the charge of electron
k_eQn_bq____ = sym.sqrt(4*sf.pi*__alpha)* k_Cn_bq____
# u0` like constant
k_u0n_bq____ = 1* k_cn_bq____**-2 / k_e0n_bq____
k__sAlpha_n_bq____ = k_eQn_bq____**2/(k_hn_bq__bq____ * k_cn_bq____)
# *****************************************************************************
# **** define modified Natural an unit charge assigned to elementary charge ****
# ==== D == E
# ==== No Vk because e0k` coverts
# *****************************************************************************
# define length:mn`
_unitConstantGlb = __dctGlb['k_c_bq____'] * __dctGlb['k_h_bq__bq____']/__eV
k_mk_bq____ = ClLllUnit('meter_k','mk`')
# define mass:gn`
_unitConstantGlb = __eV/__dctGlb['k_c_bq____'] **2
k_gk_bq____ = ClLllUnit('gram_k','gk`')
# define time:sn`
_unitConstantGlb = __dctGlb['k_h_bq__bq____']/__eV
k_sk_bq____ = ClLllUnit('second_k','sk`')
# define electron volt :eVn`
_unitConstantGlb = __eV
k_eVk_bq____ = ClLllUnit('electronVolt_k','eVk`')
# define Lorentz Heaviside electric charge:Cn`
_unitConstantGlb = __dctGlb['k_eQ_bq____']
k_Ck_bq____ = ClLllUnit('Coulomb_k','Ck`')
# deived units
# force Newton
k_Nk_bq____ = 1* k_gk_bq____ * k_mk_bq____ * k_sk_bq____ **-2
# energy Joule
k_Jk_bq____ = 1* k_gk_bq____ * k_mk_bq____**2 * k_sk_bq____ **-2
# Voltage
#k_dVk_bq____ = 1* k_gk_bq____ * k_mk_bq____ **2 * k_sk_bq____ **-2 * k_Ck_bq____**-1
k_dVk_bq____ = 1* k_mk_bq____ **-1 * k_Ck_bq____
# e0` like constant. hk`` ck` == k_Nk_bq____ * k_mk_bq____**2
k_e0k_bq____ = 1*k_Ck_bq____**2 /(4* sf.pi*k__sAlpha__bq____ * k_Nk_bq____
* k_mk_bq____**2)
#k_Vk_bq____ = k_dVk_bq____ / k_e0k_bq____ 2012.10.12
k_Vk_bq____ = k_dVk_bq____ * k_Nk_bq____ * k_mk_bq____**2/ k_Ck_bq____**2
# mLght:meter of light:unit length of light --- pure imaginary number
k_mLk_bq____ = sym.I * k_mk_bq____
# physical constant
# light velocity
k_ck_bq____ = 1* k_mk_bq____ / k_sk_bq____
# h`/(2pi)
k_hk_bq__bq____ = 1* k_gk_bq____ * k_mk_bq____ ** 2/ k_sk_bq____
# the charge of electron
k_eQk_bq____ = k_Ck_bq____
# u0` like constant
k_u0k_bq____ = 1* k_ck_bq____**-2 / k_e0k_bq____
k__sAlpha_k_bq____ = k_eQk_bq____**2/(k_hk_bq__bq____ * k_ck_bq____)
# *****************************************************************************
# **** define Planck units ****
# *****************************************************************************
# define Planc length
_unitConstantGlb = sf.sqrt(
__dctGlb['k_h_bq__bq____'] * __dctGlb['k_gU_bq____']
/__dctGlb['k_c_bq____']**3)
k_mp_bq____ = ClLllUnit('meter_p','mp`')
# Planck time: mp`/c`: sqrt(h`` c`/gU`)
_unitConstantGlb = k_mp_bq____.m_toSI / __dctGlb['k_c_bq____']
k_sp_bq____ = ClLllUnit('second_p','sp`')
# Planck mass: sqrt(h`` c`/gU`)
_unitConstantGlb = sym.sqrt(
__dctGlb['k_h_bq__bq____']* __dctGlb['k_c_bq____']
/__dctGlb['k_gU_bq____'] )
k_gp_bq____ = ClLllUnit('gram_p','gp`')
# Planck Charge: eQ`/sqrt(4pi α`)
_unitConstantGlb = __dctGlb['k_eQ_bq____']/sf.sqrt(4* sf.pi * __alpha)
k_Cp_bq____ = ClLllUnit('Coulomb_p','Cp`')
# **** define `c, h`, eQ`, (eQ`^2/(4pi ε0` h`` c`)):Fine structure constant == 1 ****
# deived units
k_Np_bq____ = 1* k_gp_bq____ * k_mp_bq____ * k_sp_bq____ **-2
# Vp` Voltage has both of mechanical units and electro-magnetic units
# Vp` means a potential difference that is the unit energy: m c^2 for the unit charge and mass.
# <== Charge * Voltage == Energy
k_Vp_bq____ = 1* k_gp_bq____ * k_mp_bq____ **2 * k_sp_bq____ **-2 * k_Cp_bq____**-1
k_dVp_bq____ = 1* k_mp_bq____ **-1 * k_Cp_bq____
# physical constant
# light velocity
k_cp_bq____ = 1* k_mp_bq____ / k_sp_bq____
k_hp_bq__bq____ = 1* k_gp_bq____ * k_mp_bq____ ** 2/ k_sp_bq____
k_eQp_bq____ = sym.sqrt(4*sf.pi*__alpha)* k_Cp_bq____
k__sAlpha_p_bq____ = k_eQp_bq____**2/(k_hp_bq__bq____ * k_cp_bq____)
# *****************************************************************************
# **** define Stoney units:http://en.wikipedia.org/wiki/Natural_units ****
# *****************************************************************************
# define Stoney length: sqrt( G e^2/(c^4 4pi e0) )
_unitConstantGlb = sf.sqrt(
__dctGlb['k_gU_bq____']*__dctGlb['k_eQ_bq____']**2
/(__dctGlb['k_c_bq____']**4* 4*sf.pi* __dctGlb['k_e0_bq____'])
* __dctGlb['k_J_bq____'] / __dctGlb['k_s_bq____'] / __dctGlb['k_W_bq____']
)
k_ms_bq____ = ClLllUnit('meter_s','ms`')
# Stoney time: mp`/c`: sqrt(h`` c`/gU`)
_unitConstantGlb = k_ms_bq____.m_toSI / __dctGlb['k_c_bq____']
k_ss_bq____ = ClLllUnit('second_s','ss`')
# Stoney mass: sqrt( e^2/(G 4pi e0)
_unitConstantGlb = sf.sqrt(
__dctGlb['k_eQ_bq____']**2
/(__dctGlb['k_gU_bq____']* 4*sf.pi* __dctGlb['k_e0_bq____'])
* __dctGlb['k_J_bq____'] / __dctGlb['k_s_bq____'] / __dctGlb['k_W_bq____']
)
k_gs_bq____ = ClLllUnit('gram_s','gs`')
# Planck Charge: eQ`/sqrt(4pi α`)
_unitConstantGlb = __dctGlb['k_eQ_bq____']
k_Cs_bq____ = ClLllUnit('Coulomb_s','Cs`')
# **** define `c, h`, eQ`, (eQ`^2/(4pi ε0` h`` c`)):Fine structure constant == 1 ****
# deived units
k_Ns_bq____ = 1* k_gs_bq____ * k_ms_bq____ * k_ss_bq____ **-2
k_Vs_bq____ = 1* k_gs_bq____ * k_ms_bq____ **2 * k_ss_bq____ **-2 * k_Cs_bq____**-1
k_dVs_bq____ = 1* k_ms_bq____ **-1 * k_Cs_bq____
# physical constant
# light velocity
k_cs_bq____ = 1* k_ms_bq____ / k_ss_bq____
k_hs_bq__bq____ = (1/__alpha)* k_gs_bq____ * k_ms_bq____ ** 2/ k_ss_bq____
k_eQs_bq____ = k_Cs_bq____
k__sAlpha_s_bq____ = k_eQs_bq____**2/(k_hs_bq__bq____ * k_cs_bq____)
"""'
'"""
def RttS(theta, axis=[1,1]):
"""' Return a rotating matrix. "axis" parameter defines the reference
axises for the rotation and also define the matrix size.
"theta" parameter represents counter clock wise rotation. Complex theta
means a Lorentz matrix.
You should set 1 just 2 times in the axis parameter sequence which indicates
rotating axis
e.g.
Rtt(`i pi/3)
===============================
[[ 1.60028686-0.j 0.00000000+1.24936705j]
[-0.00000000-1.24936705j 1.60028686-0.j ]]
---- ClTensor ----
Rtt(pi/3, [1,0,0,1])
===============================
[[ 0.5 0. 0. 0.8660254]
[ 0. 0. 0. 0. ]
[ 0. 0. 0. 0. ]
[-0.8660254 0. 0. 0.5 ]]
---- ClTensor ----
'"""
axisAt = list(axis)
sizeAt = len(axisAt)
firstIndexAt = axisAt.index(1)
secondIndexAt = axisAt.index(1, firstIndexAt+1)
import sympy
assert sf.__dctGlobals['ts'] == sympy
r1=sympy.Rational(1)
mtAt = sf.kzrs(sizeAt, sizeAt, ftype=type(1.0*r1) )
mtAt[firstIndexAt, firstIndexAt] = sf.cos(theta) * r1
mtAt[firstIndexAt, secondIndexAt] = sf.sin(theta) * r1
mtAt[secondIndexAt, firstIndexAt] =-sf.sin(theta) * r1
mtAt[secondIndexAt, secondIndexAt] = sf.cos(theta) * r1
return mtAt
sf.__getDctGlobals().update(locals())
def Rtt(theta, axis=[1,1]):
axisAt = list(axis)
sizeAt = len(axisAt)
firstIndexAt = axisAt.index(1)
secondIndexAt = axisAt.index(1, firstIndexAt+1)
import numpy as np
if np.iscomplex(theta):
# complex matrix:Lorentz transformation matrix
mtAt = sf.kzrs(sizeAt, sizeAt, complex)**0
else:
# real matrix: normal ratating matrix
mtAt = sf.kzrs(sizeAt, sizeAt)**0
mtAt[firstIndexAt, firstIndexAt] = sf.cos(theta)
mtAt[firstIndexAt, secondIndexAt] = sf.sin(theta)
mtAt[secondIndexAt, firstIndexAt] =-sf.sin(theta)
mtAt[secondIndexAt, secondIndexAt] = sf.cos(theta)
return mtAt
def mnl(v):
"""' Normalize vector v at Minkowski space.
mnl(.) returns a v direction vector of that product with itself is -1
example
mnl([0.8, 0.1, 0.2, `i])
===============================
[ 1.43684242+0.j 0.17960530+0.j 0.35921060+0.j 0.00000000+1.79605302j]
---- ClTensor ----
mnl([0.8, 0.1, 0.2])
===============================
[ 0.+0.96308682j 0.+0.12038585j 0.+0.24077171j]
---- ClTensor ----
'"""
if not isinstance(v, sf.ClTensor):
v = sf.krry(v)
assert v * v < 0, "You set a space like vector:"+str(v)
return 1j*v/sf.sqrt(v*v)
def Lvv(vcVelocity):
"""' Boost Lorentz transformation for the velocity vector in natural unit
examples
Lvv(0.8)
===============================
[[ 1.66666667+0.j 0.00000000-1.33333333j]
[ 0.00000000+1.33333333j 1.66666667+0.j ]]
---- ClTensor ----
Lvv([0.8])
===============================
[[ 1.66666667+0.j 0.00000000-1.33333333j]
[ 0.00000000+1.33333333j 1.66666667+0.j ]]
---- ClTensor ----
Lvv([0.8,0.1])
===============================
[[ 1.67968838+0.j 0.08496105+0.j 0.00000000-1.35224681j]
[ 0.08496105+0.j 1.01062013+0.j 0.00000000-0.16903085j]
[ 0.00000000+1.35224681j 0.00000000+0.16903085j 1.69030851+0.j ]]
---- ClTensor ----
Lvv([0.8,0.1, 0.2])
===============================
[[ 1.73836802+0.j 0.09229600+0.j 0.18459200+0.j 0.00000000-1.43684242j]
[ 0.09229600+0.j 1.01153700+0.j 0.02307400+0.j 0.00000000-0.1796053j ]
[ 0.18459200+0.j 0.02307400+0.j 1.04614800+0.j 0.00000000-0.3592106j ]
[ 1.43684242j 0.1796053j 0.3592106j 1.79605302+0.j ]]
---- ClTensor ----
'"""
"""'
if isinstance(vcVelocity,float):
vcVelocity = [vcVelocity]
assert sf.norm(vcVelocity) < 1
N=len(vcVelocity)
n2 = sf.normalize(vcVelocity)
E = sf.kzrs(N,N)**0
n1 = sf.kzrs(N)
n1[0] = 1
nm = sf.normalize(n1+n2)
R = (E - 2*n2**n2) * (E-2*nm**nm)
RR = sf.kzrs(N+1,N+1)**0
RR[:N, :N] = R
axis=sf.kzrs(N+1)
axis[0], axis[-1]=1,1
return RR* Rtt(sf.arctan(sf.norm(vcVelocity)/1j), axis)* RR**-1
'"""
# implementing by diadic
if isinstance(vcVelocity,float):
vcVelocity = (vcVelocity,1j)
else:
vcVelocity = tuple(vcVelocity)+(1j,)
assert sf.norm(vcVelocity[:-1]) < 1
N=len(vcVelocity)
#n2,n1=mnl(vcVelocity),[0,0,0,1j]
n2,n1=mnl(vcVelocity),[0]*(N-1)+[1j]
nm=mnl(n1+n2)
E=sf.kzrs(N,N)**0;
return (E+2*n2**n2)*(E+2*nm**nm)
def k__Round_JM___(fnAg, inDim=None, outDim=None):
"""' Jacobian at Minkowski space
'"""
clAt = sf.Jc_(fnAg,inDim,outDim) # ∂J Jacobian
def __inner(*posAg):
mtAt = sf.krry(clAt(*posAg), dtype=complex)
shapeAt = mtAt.shape
for indx_1 in sf.mitr(*shapeAt[:-1]):
for k in range(shapeAt[-1]):
if isinstance(indx_1,int):
mtAt[(indx_1, k )] *=1/(1j)
else:
mtAt[indx_1+(k,)] *=1/(1j)
return mtAt
return __inner
def k__bq_rotM___(fVct, **kwAg):
"""' rot(..) function at Minkowski space
'"""
def __inner(*pos):
mtAt = k__Round_JM___(fVct,**kwAg)(*pos) # `rot
return mtAt - mtAt.T
return __inner
===============================
None
Python を御存知の方ならば、このソース・コードを少し修正するだけで、atomic unitsなど望みの単位系を容易に修正実装できると思います。
自然単位系・Planck 単位系・Stoney 単位系では e0,u0 の値は 1 になります。このことは、e0,u0 を、冗長な単位系での単位変換定数とみなせることを意味します。
距離、時間、質量、電荷の四つを基本単位とすることで、Maxwell の作った emu 単位系「すなわち距離、時間、質量の三つのみを基本単位とする単位系」のときの単位系に 1/2 べき乗が出てくる弊害を避けられます。でも四つの基本単位を採用する代償として、単位系の冗長性が出てきます。
例として、電荷どうしに働く力 == 質量 x 加速度 == 電荷^2/(4pi 距離^2) の公式で考えてみましょう。有理化された自然・Planck・Stoney 単位系では、この公式は下のようになります。
# 電荷どうしに働く力 == 質量 x 加速度 == 電荷^2/(4pi 距離^2)
[force] == g m s^-2 == [C^2/(4pi m^2)] == C^2 m^-2
g m s^-2 と C^2 m^-2 は単位は異なるが同じ力と言う物理量を表しているとみなせます。そして e0n は この二つの単位に対する単位換算定数とみなせます。
PythonSf ワンライナー
tt(); e0n`
===============================
Cn`**2*sn`**2/(gn`*mn`**3)
このように考えると、力の単位が g m s^-2 であると同時に C^2 m^-2 にもなってしまいます。
今度は電圧を考えてみましょう。クーロンの公式から、単位電荷が単位距離の位置に作る電圧の単位は下のように C/m になります。
[Voltage:dV] == [C/(4pi m)] == C/m
一方で、エネルギー == 電荷 ・ 電圧の関係から、電圧 == エネルギー/電荷とみなせます。次の電圧単位 V: g m^2/(C s^2) も考えられます。
[V] == g (m/s)^2/C == g m^2/(C s^2)
この電圧単位は、機械系の物理量であるエネルギーと電気系の物理量の電荷で構成されています。この電圧単位は機械系と電気系両方にまたがっている単位とみなせます。
以上の考察より、四つの基本単位を採用したことに伴う冗長性から「電圧の単位を C/m と g m^2/(C s^2) どちらで表しても許される」とみなせます。そのように考え、自然単位系・修正自然単位系・Planck単位系・Stoney単位系の四つとも、誘導単位である電圧の単位として dV と V の二つを定義してあります。
PythonSf ワンライナーたち
tt(); `print([dVn`,dVk`,dVp`,dVs`])
[Cn`/mn`, Ck`/mk`, Cp`/mp`, Cs`/ms`]
===============================
None
tt(); `print([Vn`,Vk`,Vp`,Vs`])
[gn`*mn`**2/(Cn`*sn`**2),
0.0917026917931351*gk`*mk`**2/(Ck`*sk`**2),
gp`*mp`**2/(Cp`*sp`**2),
gs`*ms`**2/(Cs`*ss`**2)]
None
dV と V が同じ物理量を表しているといっても、計算上 dV/V は無次元の 1 ではありません。でも無次元の 1 でないことは冗長性によるものであり、本質的には dV/V の次元が無次元の 1 でもあると看做すこともできます。それを利用すると C^2/(4pi 1m^2) は見た目には力の単位次元ではありませんが、dV/V を掛けることによって、明示的に力の単位の次元に変換すると解釈できます。PythonSf では、冗長性のある単位系 MKSAV 単位系で、 J`/s`/W` を掛けることで同等で見慣れた単位系に変換する操作をしていますが、それと同様なことを dV/V で行わせるわけです。
PythonSf ワンライナーたち
tt(); Vk`/dVk`
===============================
0.0917026917931351*gk`*mk`**3/(Ck`**2*sk`**2)
tt(); r=1mk`; Ck`^2/(4pi r^2)
===============================
0.0795774715459477*Ck`**2/mk`**2
# 単位距離離れた単位電荷どうしの間に働く力
tt(); r=1mk`; Ck`^2/(4pi r^2) Vk`/dVk`
===============================
0.00729746834685502*gk`*mk`/sk`**2
# 単位距離離れた単位電荷どうしの間に働く力の SI 単位系での値
# すなわち 1.97-7*m` 離れた電子どうしの間に働く力
tt(); r=1mk`; toSI(Ck`^2/(4pi r^2) Vk`/dVk`)
===============================
5.92520026849261e-15*kg`*m`/s`**2
dV の単位で表したほうが良いときもあります。分極電流:j=∂t(e0 E) では dV/m == C/m^2の単位で考えるべきでしょう
二つの電圧 V と dV を冗長性による表記の多重性と看做す代わりに別の物理量であると解釈して、SI 単位系でのように 誘電率の単位の次元を持つ変換定数 e0 を導入することも可能です。このほうが dV == C/m を分極の程度を表す単位と看做せるので、便利なことも多いでしょう。その代償として物理的には同じであるのに B と H が別物と看做さねばならなくなります。でも、これは SI 単位系で慣らされているので、問題とはされないでしょう。
PythonSf ワンライナーたち
tt(); e0n`, e0k` # e0p`, e0s`
===============================
(Cn`**2*sn`**2/(gn`*mn`**3), 10.904805305561*Ck`**2*sk`**2/(gk`*mk`**3))
tt(); r=1mn`; Cn`^2/(4pi e0n` r^2)
===============================
0.0795774715459477*gn`*mn`/sn`**2
tt(); r=1mk`; Ck`^2/(4pi e0k` r^2)
===============================
0.00729746834685502*gk`*mk`/sk`**2
tt(); r=1mn`; toSI(Cn`^2/(4pi e0n` r^2))
===============================
6.46131553243694e-14*kg`*m`/s`**2
tt(); r=1mk`; toSI(Ck`^2/(4pi e0k` r^2))
===============================
5.92520026849261e-15*kg`*m`/s`**2
tt(); Vk`, Ck`/mk` /e0k`
===============================
(0.0917026917931351*gk`*mk`**2/(Ck`*sk`**2),
0.0917026917931351*gk`*mk`**2/(Ck`*sk`**2))
自然単位系では e0 を導入しても、その値は 1 にすぎません。D=dV/m,E=V/m に対応する H,B が考えられますが、それらは単位が異なるだけで、常に同じ値です。ですから gauss 単位系のときの oersted/gauss のように、電流に起因する磁場に oersted:H、磁石に起因する磁場に gauss:B を対応させ、両者は同じものだと考える使い方ができます。
一方で素電荷を単位電荷とする修正自然単位系では e0k`:10.9*Ck`**2*sk`**2/(gk`*mk`**3) の 11 に近い値を持つ物理定数が入り込んできます。H と B の値が一桁程度異なってしまいます。ならば SI 単位系でのように H と B を別物とみなし u0k`=1/(ck`^2 e0k`) 定数を導入することも可能です。こうすることで SI 単位系で書かれた電磁気学の教科書に書かれてある公式を、そのまま利用できる利点を得られます。
このように考えて、自然単位系と修正自然単位系では、e0n`,e0k` と u0n`,u0k` の物理定数を定義してあります。Planck 単位系と Stoney 単位系では、これらの物理定数を定義してありません。実用的に使える単位系ではないと考えるからです。必要な方は御自分で追加ください。
SI 単位系の規格書は理由を示すことなく、天下りに定義を提示・羅列していきます。結果として下のような疑問が残ったままになります。物理の教師でも、これらの疑問に答えられる方は、殆どいないと思います。
本来、なんらかの物理理論を理解したならば、そこで出てくる物理量の単位系全てが、基本単位系から導出できるようになっているはずです。弾性力学を理解したならば、その応力は Pa == N/m^2 == kg m/s^2 /m^2 == kg /(s^2 m) であることが、教科書を読み返すことなく、すらすらと出てくるはずです。そうでなければ弾性力学を理解したとはいえません。
一方で電磁気学を理解した方たちでも「抵抗==kg*m**2/(A**2*s**3)誘導単位」を基本単位から導出できないのが実情でしょう。しかし ここでの自然単位系、修正自然単位系を理解できれば、これが可能になります。
修正自然単位系は自然です。自然単位系での単位電荷 Cn` は 長さ・質量・時間:LMT と微細構造定数から定めた物理量です。その物理的な意味は説明できません。でも修正自然単位系での単位電荷 Ck` は電子の電荷です。自然から与えられた基本量です。長さ:m や時間 s よりも、単純で説得性のある基本単位です。この基本単位からの誘導単位の導出が、以下のように自然に行われます。
以下、訳のわからん SI 単位系の値を基本単位から自然に、論理的に導いていきます。
SI 単位系の作成者たちも修正自然単位系を考えたことがあるはずです。素電荷:電子の電荷が given であるとして、先に e0 を explicit に導出してから、その後で u0 を導出したはずです。
「e0n`,e0k` と u0n`,u0k`」での説明にあるように、クーロンの法則「力=g m/s^2 == C^2/(4pi e0 r^2)」より真空の誘電率 C s^2/(g m^3) が explicit に導出されます。下の SI 単位系の値が explicit に導出されます。
PythonSf ワンライナー
ts(); e0`, e0` W` s`/J`
===============================
(8.854187816e-12*A`*s`/(m`*V`), 8.854187816e-12*A`**2*s`**4/(kg`*m`**3))
ただ、SI 単位系での単位電荷が、Maxwell が昔定めた 1A の電流より定まる電荷を選択せねばならなかったことより、SI 単位系の e0 は上の値の物理定数になってしまいました。
e0 が定まれば「c^2 e0 u0 == 無次元の 1」の関係より物理定数:u0 が単位も含めて explicit に導出されます。
PythonSf ワンライナー
ts(); u0` J`/s`/W`, 1/(c`^2 e0`) J`/s`/W`
===============================
(1.2566370614e-6*kg`*m`/(A`**2*s`**2), 1.25663706166589e-6*kg`*m`/(A`**2*s`**2))
この explicit に導出された u0 を元に、「単位距離だけ離れた、単位電流が流れる電線の間に働く単位長さあたりの力」が下のように 1e-7 N と計算されます。
PythonSf ワンライナー
ts(); I,r=1A`,1m`; u0`/2 I^2/(2pi r) J`/s`/W`
===============================
9.99999999971418e-8*kg`/s`**2
SI 単位系では、以上の検討過程を伏せたまま「真空の透磁率 u0 は 4pi*10^-7 kg`*m`/(A`**2*s`**2)) である」と理由を示すことなく天下りに定義を提示して単位電流を implicit に定義します。
たしかに u0 と I^2 を掛ければ電流の項は打ち消しあってなくなりますが、何もない状態で、始めから 4pi*10^-7 kg`*m`/(A`**2*s`**2)) の値と単位を出せるはずがありません。SI 単位系の作成者たちも、最初は explicit に e0 を定義し、それから u0 を定義したはずです。
SI 単位系での訳のわからん抵抗単位:kg*m**2/(A**2*s**3) が、修正自然単位系だと V/I の関係より自然に導出されます。単位電荷として自然な、その定義に悩む必要のない素電荷を採用しているからです。
電圧 == エネルギー/電荷の法則より電圧の単位が下のように定まります。
PythonSf ワンライナー
tt(); Vk`
===============================
gk`*mk`**2/(Ck`*sk`**2)
電圧の単位が定まったのならば、R = V/I の公式より抵抗の単位が下のように定まります。
PythonSf ワンライナー
tt(); Vk`/(Ck`/sk`)
===============================
gk`*mk`**2/(Ck`**2*sk`)
電流:AC = 電荷/時間 = C/s の公式を上の抵抗の単位に入れてやれば、 kg*m**2/(A**2*s**3) が出てきます。SI 単位系では理解できなかった抵抗の単位が、自然単位系、修正自然単位系では基本単位系から explicit に導出できました。
逆に、ここでのような考察を経験していない大多数のエンジニアたちは「抵抗の単位が kg*m**2/(A**2*s**3) だ」なんて受け入れられないでしょう。回路設計者に「100 kg*m**2/(A**2*s**3) の抵抗」といっても通じません。「100Ω または 100 Volt/Ampere の抵抗」 と言わねばなりません。SI 単位系が MKSA 単位系だと言っても、実際には MKSA+V:電圧:Volt 単位系で理解しているからです。大多数のエンジニアにとって抵抗の単位は Volt/Ampere だからです。電流と同様に電圧も基本単位だと大多数のエンジニアは認識しているからです。
PythonSf では基本単位に MKSA の四つではなく、MKSAV の五つを採用しています。ですから下のように普通のエンジニアに受け入れられる次のような表記になります。
PythonSf ワンライナー
ts(); 100V`, 33Ω`
===============================
(100*V`, 33*V`/A`)
一方で sympy での単位系では、SI 単位系での下の表記になってしまいます。
PythonSf ワンライナー
import sympy.physics.units as md; 100md.V, 33md.ohm
===============================
(100*kg*m**2/(A*s**3), 33*kg*m**2/(A**2*s**3))
修正自然単位系では Coulomb の法則「力 ∝ q^2/r^2」から、機械系の誘導単位である力と基本単位電荷 Ck` を結びつける物理定数 e0k` が自然に導かれます。有理化単位系を選択することで F=q^2/(4pi e0 r^2) の公式が自然に定まります。下の物理定数 e0k` と その誘導単位が自然に定まります。教科書やコンピュータに頼ることなく、基本単位長さ・質量・時間と基本単位電荷から誘導される物理量として、下の値と物理単位を論理的に導けます。
PythonSf ワンライナー
tt(); e0k`
===============================
10.904805305561*Ck`**2*sk`**2/(gk`*mk`**3)
修正自然単位系は、基本単位長さ・質量・時間は自然単位系と共通です。でも単位電荷が異なります。ですから自然単位系の e0n は 1.0 Cn`**2*sn`**2/(gn`*mn`**3) と値が 1 になるのですが、修正自然単位系 e0k` の値は 1 になりません。少し不自然さが入り込みます。逆に e0k`,u0k` が 1 にならないため、SI 単位系のときのように真空での B と H の値が異なってしまいます。逆に、このことは SI 単位系の理由を浮かび上がらせてくれます。
e0k` の誘導単位が自然だと受け入れられるならば、SI 単位系での真空の誘電率 e0 の誘導単位も自然だと受け入れられます。
PythonSf ワンライナーたち
tt(); e0n`
===============================
Cn`**2*sn`**2/(gn`*mn`**3)
import sympy.physics.units as md; 1.0 md.e0
===============================
2.78162514013405e-11*A**2*s**4/(pi*kg*m**3)
# 上の計算結果には pi が入っています。pi で明示的にわってやれば下の値と同じになります。
tt(); toSI(e0k`)
===============================
8.854187816e-12*A`**2*s`**4/(kg`*m`**3)
物理専攻の人間でも、上の真空の誘電率の単位:A^2 s^4/(kg m^3) を自力で導いていける方は少ないと思います。
e0 が誘導されれば、Colomb の法則から定まる電圧 = q/(4pi e0 r) より電圧の誘導単位が下のようになることも自然に導かれます。 エネルギー = 電荷 * 電圧 の関係からの行う電圧単位の誘導のほうが より直接的にも感じられます。
PythonSf ワンライナー
tt(); Vk`
===============================
0.0917026917931351*gk`*mk`**2/(Ck`*sk`**2)
Vk` の誘導単位が自然だと受け入れられるならば、SI 単位系での電圧の誘導単位も自然だと受け入れられます。
PythonSf ワンライナー
import sympy.physics.units as md; 1.0 md.V
===============================
1.0*kg*m**2/(A*s**3)
Lorentz 変換と四元ベクトル・ポテンシャルから ベクトル・ポテンシャル:A * 光速度:c の単位が電圧であることから、ベクトル・ポテンシャルの誘導単位は Vk`/(mk`/sk`) == gk`*mk`/(Ck`*sk`) であることが自然に導出されます。B==rot(A) より磁束密度の誘導単位が Vk` sk`/mk`**2 == gk`/(Ck`*sk`) であることも、自然に導出されます。
このような形で全ての電磁気学で出てくる誘導単位を、教科書やコンピュータに頼ることなく、全てを自然に導き出していけます。
私は SI 単位系の制定者たちも、ここでの修正自然単位系のことを考えていたはずだと思っています。修正自然単位系での誘導単位の導出作業を経験していたはずです。それから逆算する形で SI 単位系を定めたはずです。最初から電流定義のために u0 == 6.0e-7*pi*kg*m/(A**2*s**2) の誘導単位を出せるとは思えません。皆様は如何思われるでしょうか。
ここでは SI 単位系で質量の基本単位が g ではなく kg になった理由を論じます。
kg が単位質量になったのは歴史的経緯によるものです。Maxwell が定めた実用電流単位:A、電圧単位:V が CGS 単位系とは合わないため MKS 単位系が使われたからです。その MKS 単位系を SI 単位系が採用したためです。
Mawell が cgs 単位系を前提に emu 単位系を定めました。でも emu 単位系での単位電圧は 10^-8V、単位抵抗は 10^-9Ω と極端に小さな値でした。emu 単位系での単位電流は 10A と SI 単位系での値と一桁しか違わないのですが。ですから Maxwell は当時の電気の応用の主流であった有線通信で使われていた電流・電圧・抵抗に合わせた実用単位を定義しました。すなわち emu 単位系での単位電圧の 10^8 倍を実用電圧値としました。emu 単位系での単位抵抗の 10^9 倍を実用抵抗値としました。emu 単位系での単位電流の 10^-1 倍を実用電流値としました。実用抵抗値を持つ標準抵抗を白金で作り配布しました。元々、 V,Ω,A は、k,M,G などのような桁数の意味の記号でした。その実用値は、当時の無線通信での抵抗値:大地の抵抗、電圧値:Volta 電池の値、電流値:コイル・スイッチを引き付ける電流の値に近い emu 単位系の 10^N で定まる値でした。しかし実用単位ばかりを使うエンジニアたちは V,Ω,A を桁数の意味ではなく、単位電圧・単位抵抗・単位電流の意味で使うようになりました。
一方で 19 世紀の末になると電気の応用分野の主流がは有線通信から発電機やモータの分野に変わってきました。ここで Volt,Ampere と cgs 単位系が矛盾するようになってきました。Eenergy = J` = V` A` s` == W` s` が cgs のエネルギー単位 erg の 10^7 倍の値になってしまうのです。エネルギーだけならば 10^7 係数一つかければ済むのですが、力、角運動量など電気系と機械系の接するところ全てで、様々の係数を掛ける必要にせまられました。本来ならば設計で使っているような単位系など変えずに使い続けたいのですが、電気系と機械系が組み合わさった装置を作るようになると単位系を変えたほうを選択せざるをえなくなりました。そこで M K S 単位系が必要になりました。cgs 単位系から修正するとき cm → m, gram → kg のほうが cm → 10^7cm=10^5m, gram → gram よりも単純であり MKS が選択されました。
ここの説明で「19世紀の終わりに重厚長大産業が発達したために MKS 単位系が使われるようになった」とするものがありますが、これは誤りです。重機械の設計でも使われるのは mm 単位です。その上で 0.1mm 以下の精度で作らないと、大部分の機械は動きません。もともと扱う対象のサイズが大きくなったぐらいでは、それまで使ってきた単位系を変更しません。 「重工業が発達して大きな機械が使われるようになったから」ではなく、「発電機やモータなどの機械系と電気系が組み合わさった装置が設計されるようになったから」MKS 単位系が導入されたのです。
そのような MKS 単位系を受け継いだ SI 単位系でも単位質量が gram ではなく kg になりました。
自然単位系、修正自然単位系を検討してみると、電磁気における e0,u0 物理定数の存在理由は C,g,m,s 基本単位の冗長性にあるのだと思います。冗長性のない emu 単位系では e0,u0 では出てこないのですから。
でも、電磁系の世界 C,m,s と機械系の世界 g,m,s の二種類が存在しているのも明白であり、C,g,m,s が冗長と言い切るのも誤っているとも思います。emu 単位系からすれば冗長ですが。機械系:g,m,s の概念であるエネルギーや運動量などの概念を電磁系:C,m,s の世界に持ち込む限りは e0,u0 の物理定数から逃れられないとも思います。SI 単位系の世界では電圧:V: g*m**2/(C*s**2) が機械系と電磁系の両方に跨る物理量なのでしょう。
でも、e0,u0 物理定数に冗長性を感じるのも拭えません。E^2 をエネルギー密度とするなど、電磁系の世界でエネルギーや運動量概念を構築しておいて機械系の世界:g,m,s と接続したら、機械系の世界の側に e0,u0 相当の物理定数が入り込むことになるからです。私には冗長性のある e0,u0 の記述しかできない人類の自然認識に、何らかの不足があるとしか思えません。もちろん emu 単位系より C,g,m,s 単位系の方が自然認識として単純になるとも思います。単位系に 1/2 乗の項が出てくるのは不自然すぎます。
遠い将来、機械系の世界:g,m,s と電磁系の世界:C,m,s を統合する物理理論ができれば不自然な e0,u0 がなくなるのだろうと思います。そのときには電荷:C・質量:g が何か新しい物理量に統合されるのだと思います。皆様はどのうよに考えますでしょうか。