29 May 2014

■■ 概要 ■■

特殊相対論で光速度に近い速さで動く物体は縮んで見えると言われます。この「縮んで見える」には光速度で光子が網膜に到達するまでの時間遅れによる効果は含まれません。

この光が到達するまでの時間による見え方の変化が Penrose Terrell Rotation と謂われる効果であり、縮むだけでなく回転も出てくるとされています。

この効果を分かりやすく「列車の速度がが光速度に近づくと、その左側にある列車でもその背面が見えてくる」とも言えます。この背面が見え始める現象を PythonSf の計算で可視化してみました。

■■ 実行環境

配布している PythonSf の sfCrrintIni.py を sfCrrntIniRelativity.Py でコピーしたものにします。 sfCrrntIniRelativity.Py にある Lorent Boost Tensor 関数 Lvv(..) を使うからです。相対論での検討を多くなさるかたは、この機会に相対論専用のディレクトリを設けておくのがよいでしょう。

Unix, Windows には依存しません。PythonSf は所詮 CUI プログラムですから。

ここでは PythonSf Open 判での計算は扱いません。そこまで知恵を回していられない計算が多いからです。

■■ 列車のモデル化

列車を次のような直線の組合せで表現し、列車の代用とします1。

直線の組合せによる列車のモデル化

lsGlb=[~[0,0,0],~[1,0,0],~[1,1,0],~[0,1,0], ~[0,1,1],~[1,1,1],~[1,0,1],~[0,0,1], ~[0,1,1],~[0,0,0],~[0,1,0],~[0,0,1], ~[0,0,0],~[1,0,1],~[1,0,0],~[0,0,1]]; v=0.8 ~[0,1,0]; plotTrajectory(lsGlb)

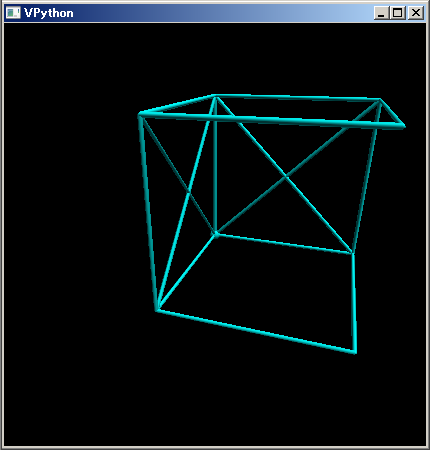
この直線の組合せが Lorentz 変換と光速度での伝播遅延でどのように歪むかを調べます。この直線の組合せ図形の方が、光の伝播時間の違いによる歪みみ具合を掴みやすいと思います。

■■ Penrose Trrell 回転

光速度の 80% の速度で動いている上の列車を、時刻 0 で [3,0,0] の位置から見たとき、Lorentz 変換と光伝播速度による遅延で下のように歪んで見えます。

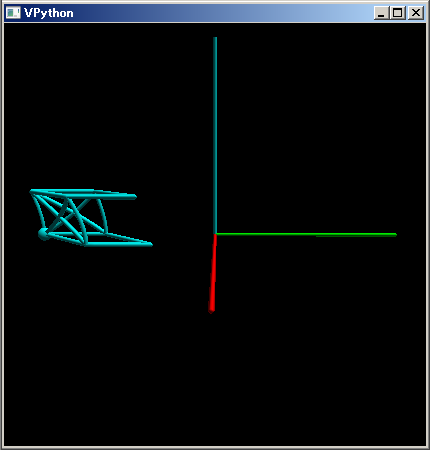
この Penrose Trrell 回転図形が何行ぐらいのコードで描けるのか予想してみてください。また自分でこの図形を描かせるプログラム・コードを書くとしたら何行ぐらいになるか、ラフで構わないので想定してみてください。下のコードはそれらよりずっと短いと思いますが、如何でしょうか。

//@@
sy()

lsGlb=~[[0,0,0],[1,0,0],[1,1,0],[0,1,0], [0,1,1],[1,1,1],[1,0,1],[0,0,1],
        [0,1,1],[0,0,0],[0,1,0],[0,0,1], [0,0,0],[1,0,1],[1,0,0],[0,0,1]]

### Lorentz transform Tensor at 0.8c` velocity
Lvv8=Lvv(-0.8 ~[0,1,0])

### A Lorentz transform function for on a train model''s space-time point that
### are specified by t, prmt, k
f=λ t,prmt=0,k=2:(Lvv8 np.r_[lsGlb[k]+prmt (lsGlb[k+1]-lsGlb[k]), `i t])

### a function that finds a time corresponding to a Lorentz transformed space-time
### specified by t, prmt, k
fnPstn=λ tt,prmt=0,k=2:(f(so.brentq(λ t:f(t,prmt,k)[3].imag -tt,-30,30), prmt,k)[:3]).real

### retarted space-point
def rtPt(posAg, prmtAg, n):
    ttAt=so.brent(λ tt:((ttGlb-tt)-norm(posAg-fnPstn(tt,prmtAg,n)))^2)
    return fnPstn(ttAt,prmtAg,n)

### view space-time point
pstn=[3,0,0]
ttGlb=0

plotTrajectory(sum([[rtPt(pstn,prmt,k) for prmt in klsp(0,1, 10)] for k in range(len(lsGlb)-1)], []))
//@@@

ちなみに、上のコードをワン･ライナーにすると下のようになります

Penrose-Trrell rotation onliner

pstn,ttGlb=[3,0,0],0; sy(); lsGlb=~[[0,0,0],[1,0,0],[1,1,0],[0,1,0], [0,1,1],[1,1,1],[1,0,1],[0,0,1], [0,1,1],[0,0,0],[0,1,0],[0,0,1], [0,0,0],[1,0,1],[1,0,0],[0,0,1]]; Lvv8=Lvv(-0.8 ~[0,1,0]); f=λ t,prmt=0,k=2:(Lvv8 np.r_[lsGlb[k]+prmt (lsGlb[k+1]-lsGlb[k]), `i t]); fnPstn=λ tt,prmt=0,k=2:(f(so.brentq(λ t:f(t,prmt,k)[3].imag -tt,-30,30), prmt,k)[:3]).real; rtPt=λ posAg, prmtAg, n:fnPstn(so.brent(λ t:((ttGlb-t)-norm(posAg-fnPstn(t,prmtAg,n)))^2), prmtAg,n); plotTrajectory(sum([[rtPt(pstn,prmt,k) for prmt in klsp(0,1, 10)] for k in range(len(lsGlb)-1)], []))

ワン･ライナーも「ここまで長くなると有害かな」とも思えてきます。Readability の意味からは、このようなワン･ライナーは使うべきではありません。

でも、このようなソフトは Python のライブラリにするほどには汎用的でありません。でも見る位置や時刻を様々に変更したときの検討結果を残していくとき、上のワン・ライナーは魅力です。そのワン・ライナーだけで何時でも過去の検討結果を再現できるのですから。

この記事の中に限定して、他の節で異なった見え方を示すときならば、上のワン･ライナーを修正したものを添付することは有効だと思います。

■■ Penrose-Trrell 図を描くコードの解説

上のコードの提示だけでは不親切すぎるとも思うので、コードの働きを関数ごとに解説します。

f:Lorentz 変換関数

関数 f(..) は、光速度の 80% の速度で動く座標系から静止座標系への Lorentz 変換を、列車モデルのワイア・フレームの各点について行う関数です。0.8C` 速度の座標系での静止しているワイア・フレームの各時空ポイントは点は prmt∈[0,1) の実数とフレーム直線の端点を表す自然数 k です。

fnPstn: 静止座標系での列車の空間座標を返す関数

fnPstn は、静止座標系での指定時刻における、静止座標系での列車の空間座標を返す関数です prmt と k で定められるワイア･フレーム上の位置が、静止座標系で時刻 tt で観測されるときの静止座標系での空間座標を見つけ出して返します。

列車に固定した座標系では、ワイア･フレーム上の位置が一旦指定されると、その空間座標は固定され、時間座標のみが変化します。しかし移動する列車を観測している静止座標系から未定いると、指定されるワイア･フレーム上の位置は時刻と一緒に変化していきます。この変化は Loretz 変換テンソルで計算できます。

rtPt: 静止座標系での光の伝播遅延も含めた空間座標を返す関数

rtPt は、時刻 ttGlb で posAg 位置から列車を光の伝播遅延も含めて観測した時、prmt, k 引数に対応した静止座標系での空間座標を返す関数です。単純化するため、光速度が 1 の単位系で考えています。prmt, k で指定されたワイアー・フレーム位置の静止座標系での時空座標 [posAt, ttAt] で発行された光が [posAg, 時刻 ttGlb] で観測されるならば (ttGlb-ttAt) == norm(posAg - posAt) となる、すなわち |(ttGlb-ttAt) - norm(posAg - posAt)|^2 が最小値となることより posAt を求めています。その最小値となる ttAt parameter を求めために scipy.optimize モジュールにある brent(..) 関数を利用しています。

■■ Lorentz 変換のみによる列車の変形

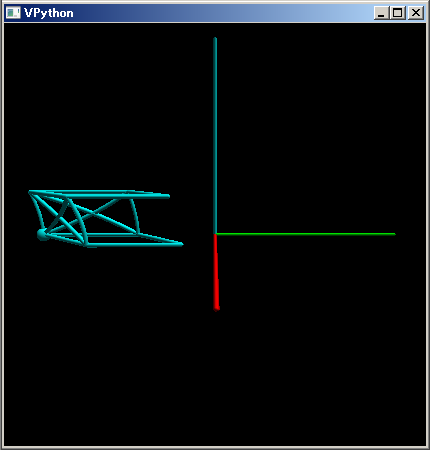
光の伝播遅延を含まない Lorentz 変換のみによる列車の変形は下のようになります。

Lorentz 変換のみによる列車の変形

//@@
sy()

### Points of a Train Model
lsGlb=~[[0,0,0],[1,0,0],[1,1,0],[0,1,0], [0,1,1],[1,1,1],[1,0,1],[0,0,1],
        [0,1,1],[0,0,0],[0,1,0],[0,0,1], [0,0,0],[1,0,1],[1,0,0],[0,0,1]]

### Lorentz transform Tensor at 0.8c` velocity 
Lvv8=Lvv(0.8 ~[0,1,0])

### A Lorentz transform function for on a train model''s space-time point that are specified by t, prmt, k
f=λ t,prmt=0,k=2:(Lvv8 np.r_[lsGlb[k]+prmt (lsGlb[k+1]-lsGlb[k]), `i t])

### a function that finds a time corresponding to a Lorentz transformed space-time specified by t, prmt, k
g=λ tt,prmt=0,k=2:(f(so.brentq(λ t:f(t,prmt,k)[3].imag -tt,-9,9), prmt, k)[:3]).real

plotTrajectory(sum([[g(0, prmt, k) for prmt in klsp(0,1, 10)] for k in range(len(lsGlb)-1)], []))
//@@@

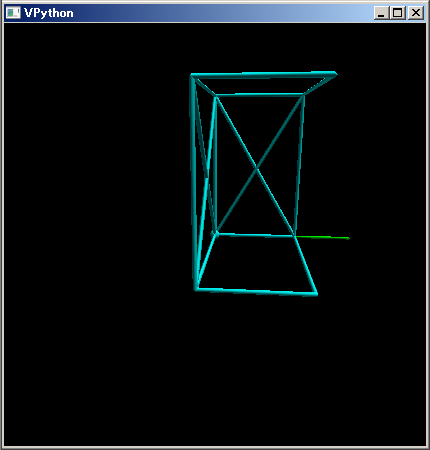
光の伝播遅延遅延を考慮しないときは、進行方向に対して縮んでいるだけです。

この長方形の図を見ていると、列車の背面から出た光は側面にブロックされて見えないように誤解してしまう方がいるかもしれません。私がそうでした。日常の光が無限大のスピードとみなせるときの直感による誤解でした。

この場合の列車は光の 8 割の速度で動いているので \( \theta = arctan(0.8) \) の視野角以下の位置から見ていれば列車の背面が見えます。

■■ 検討

Penrose-Trrell rotation と言われますが、私は「回転と言うより回転に似たように錯覚させる菱形変形」と言うべきだと主張します。またこの菱形変形の効果は Lorentz 変換ではなく、光の伝播遅延によるものです。

球の Penrose-Trrell 回転

列車のワイア･フレーム場合は、上面の変形を見ていれば菱形変形だと直ぐに気付くと思います。たぶん rotation の言葉が出てきたのは色が一様な球の変形をイメージしていたせいだと推測しています。このときは菱形変形にも関わらず球に見えているからでしょう。

球の Penrose-Trrell 回転

pstn,ttGlb=[3,0,0],0; sy(); lsGlb=~[[sin(θ)cos(φ),sin(θ)sin(φ), (-1)^k cos(θ)] for k,φ in enumerate(klsp(0,2pi,13)) for θ in klsp(0,pi,10)]; Lvv8=Lvv(-0.8 ~[0,1,0]); f=λ t,prmt=0,k=2:(Lvv8 np.r_[lsGlb[k]+prmt (lsGlb[k+1]-lsGlb[k]), `i t]); fnPstn=λ tt,prmt=0,k=2:(f(so.brentq(λ t:f(t,prmt,k)[3].imag -tt,-30,30), prmt,k)[:3]).real; rtPt=λ posAg, prmtAg, n:fnPstn(so.brent(λ t:((ttGlb-t)-norm(posAg-fnPstn(t,prmtAg,n)))^2), prmtAg,n); plotTrajectory(sum([[rtPt(pstn,prmt,k) for prmt in klsp(0,1, 10)] for k in range(len(lsGlb)-1)], []))

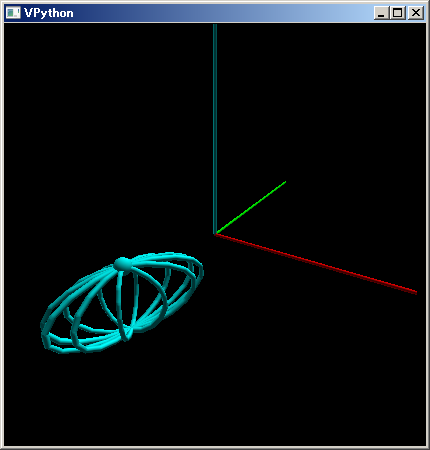
でも球のワイア・フレームを二つの円だけに簡素化してみると球のときも菱形変形であることが判ります。一方の球は回転していないのですから。 Penrose-Trrell 回転では球の反対側はどんなに光速度に近づけても見えません。

二つの円の Penrose-Trrell 回転

pstn,ttGlb=[3,0,0],0; sy(); lsGlb=~[[sin(θ)cos(φ),sin(θ)sin(φ), (-1)^k cos(θ)] for k,φ in enumerate(klsp(0,2pi, 5)) for θ in klsp(0,pi,10)]; Lvv8=Lvv(-0.8 ~[0,1,0]); f=λ t,prmt=0,k=2:(Lvv8 np.r_[lsGlb[k]+prmt (lsGlb[k+1]-lsGlb[k]), `i t]); fnPstn=λ tt,prmt=0,k=2:(f(so.brentq(λ t:f(t,prmt,k)[3].imag -tt,-30,30), prmt,k)[:3]).real; rtPt=λ posAg, prmtAg, n:fnPstn(so.brent(λ t:((ttGlb-t)-norm(posAg-fnPstn(t,prmtAg,n)))^2), prmtAg,n); plotTrajectory(sum([[rtPt(pstn,prmt,k) for prmt in klsp(0,1, 10)] for k in range(len(lsGlb)-1)], []))

回転のような効果が見られるのは、光の伝播遅延が主要な理由であり、Lorentz 変換による変形無関係だとさえ言えます。下のように Lorentz 変換ではなくGalilei 変換でも光の伝播遅延を付け加えれば同様な歪みが発生するからです。

Gallilei 変換における、光の伝播遅延がもたらす菱形変形の効果

この菱形変形の効果は Lorentz 変換ではなく、光の伝播遅延によるものです。Lorentz 変換ではなく、Gallilei 変換でも菱形変形は発生するからです。

Gallilei 変換と光の伝播遅延による列車の変形

//@@
sy()

lsGlb=~[[0,0,0],[1,0,0],[1,1,0],[0,1,0], [0,1,1],[1,1,1],[1,0,1],[0,0,1],
        [0,1,1],[0,0,0],[0,1,0],[0,0,1], [0,0,0],[1,0,1],[1,0,0],[0,0,1]]

v=0.8 ~[0,1,0]
fnPstn= λ t,prmt=0, k=2: lsGlb[k]+ prmt (lsGlb[k+1]-lsGlb[k])+ t v
def rtPt(posAg, prmtAg, n):
    tAt=so.brent(λ t:(-t-norm(posAg-fnPstn(t,prmtAg,n)))^2)
    return fnPstn(tAt,prmtAg,n)

pstn=[3,0,0]
plotTrajectory(sum([[rtPt(pstn,prmt,k) for prmt in klsp(0,1,10)] for k in range(len(lsGlb)-1)], []))
//@@@