PythonSf による有限体八元数の置換群操作と その対称性--jpn one-liners
はじめに:代数系のおもちゃ箱
PythonSf は one-liner で計算するツールです。数学が関連する全ての分野で使えます。使えるようにできます。
本稿では代数系での計算に注目してみます。本稿では PythonSf の置換群:Sb, Cy, extend, 有限体八元数:O2,O3,O4,O5,O6,O7,Ob の道具を使います。実際に有限体八元数を Sb 置換によって置き換え操作を行います。これらの集合の置換操作により、幾何学図形における対称構造が有限体にも備わっていることを具体例で示します。これらのツールの組み合わせは一生かけても遊び尽くせない数学のおもちゃ箱にできることを示します。
以下で実際に計算するのは全て PythonSf one-liners です。短い one-liners でも可読性を犠牲にすることなく、代数での群論的考察を積み重ねていく様子を見てやってください。また One-liners が人間の思考の粒度に注目してやってください。
PythonSf one-liners と mitr:多重イタレータ
PythonSf one-liner は複数の Python 文を実行できますが、それらはインデントなしプログラムでなければなりません。すなわち if 文を使わない:(変わりに条件式:”conditional expression” は多用します。)、多重ループを使わないコードにしなければなりません。数学的対象の Python プログラミングでは、if 文よるプログラムの流れ制御は殆ど必要ありません。リスト内包表記の if 条件式があれば十分です。多重ループを必要とすることは数学だからこそ多いのですが、それには mitr:多重イタレータを活用することで、インデント無しのコードにできます。
mitr:多重イタレータは PythonSf 特有の多用されるイタレータなので、ここで説明しておきます。mitr(3,4) iterator は下の Python code と殆ど殆ど同じ繰り返しを行います
Python code
//@@
for j in range(3):
for k in range(4):
print (j,k),
//@@@
(0, 0) (0, 1) (0, 2) (0, 3) (1, 0) (1, 1) (1, 2) (1, 3) (2, 0) (2, 1) (2, 2) (2, 3)
mitr(3,4) が上のコードと同様な pair tuple を返すことは下の PythonSf one-liners で確認できます。mitr(..) 関数は可変長引数関数なので、任意回数の多重ループを一回の呼び出しだけで記述できます。
PythonSf/Op one-liners
list(mitr(3,4))
===============================
[(0, 0), (0, 1), (0, 2), (0, 3), (1, 0), (1, 1), (1, 2), (1, 3), (2, 0), (2, 1), (2, 2), (2, 3)]
list(mitr(3,4,2))
===============================
[(0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (0, 2, 0), (0, 2, 1), (0, 3, 0), (0, 3, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1), (1, 2, 0), (1, 2, 1), (1, 3, 0), (1, 3, 1), (2, 0, 0), (2, 0, 1), (2, 1, 0), (2, 1, 1), (2, 2, 0), (2, 2, 1), (2, 3, 0), (2, 3, 1)]
list(mitr(*[2]*4))
===============================
[(0, 0, 0, 0), (0, 0, 0, 1), (0, 0, 1, 0), (0, 0, 1, 1), (0, 1, 0, 0), (0, 1, 0, 1), (0, 1, 1, 0), (0, 1, 1, 1), (1, 0, 0, 0), (1, 0, 0, 1), (1, 0, 1, 0), (1, 0, 1, 1), (1, 1, 0, 0), (1, 1, 0, 1), (1, 1, 1, 0), (1, 1, 1, 1)]
mitr(..) 関数は index 上限を指示する整数引数以外に iterator instance も引数にとれます。まあ これは itertortools.product iterator と同じ働きをすることでもありますが。
群:Sb, Cy, extend,
PythonSf では群を扱う置換群:Sb, 巡回群:Cy, 集合を群に拡張する:extend の三つの関数を用意しています。逆にこれだけしか用意していませんから、高度なことはできませんが、容易に使えるようになります。高度なことはできないと言いましたが、学部生ぐらいだったら十分に近い機能を備えています。
Sb:置換クラス
Sb は置換機能を実装したクラスです。例えば Sb(1,3,0,2) は下のように 0,1,..,3 の整数を置換機能を持ちます。
0, 1, 2, 3
↓ ↓ ↓ ↓
1 3 0 2
Sb インスタンスには積演算、整数べき乗演算が備わっています。
PythonSf/Op one-liners
x=Sb(1,3,0,2); x^-1, x^2, x x^-1
===============================
(Sb(2,0,3,1), Sb(3,2,1,0), Sb(0,1,2,3))
Cy(..):巡回置換
Cy(..) は引数の整数値 tuple を巡回置換にした Sb instance を返す関数です。
Cy(n0,n1,n2, ... n_last) ≡ n0, nl, n2, ... n_last
↓ ↓ ↓ ... ↓
n1 n2 n3 n_0
Sb(..) のときとは異なり、引数に 0 を含む必要はありません。
PythonSf/Op one-liners
Cy(0,1), Cy(2,3), Cy(2,5), Cy(3,7,5), Cy(range(4))
===============================
(Sb(1,0), Sb(0,1,3,2), Sb(0,1,5,3,4,2), Sb(0,1,2,7,4,3,6,5), Sb(1,2,3,0))
Cy(0,1,2)^3 == Sb(0)
===============================
True
extend(..): グループ生成関数
extend(..) は 引数に与えられたシーケンスまたは集合データの要素どうしの積演算を繰り返し、それ以上大きくならなかったときの集合を返します。下のような具合です。Sb instance のシーケンスデータ・集合データを与えたとき、それを含む最小の群の集合を返してくれます。下のような具合です。
PythonSf/Op one-liners
extend([Cy(1,2,3)])
===============================
kfs(Sb(0,1,2,3), Sb(0,2,3,1), Sb(0,3,1,2))
N=4; extend([Cy(0,1), Cy(range(N))])
===============================
kfs(Sb(0,1), Sb(1,0), Sb(0,1,3,2), Sb(0,2,1,3), Sb(0,2,3,1), Sb(0,3,1,2), Sb(0,3,2,1), Sb(1,0,3,2), Sb(1,2,0,3), Sb(1,2,3,0), Sb(1,3,0,2), Sb(1,3,2,0), Sb(2,0,1,3), Sb(2,0,3,1), Sb(2,1,0,3), Sb(2,1,3,0), Sb(2,3,0,1), Sb(2,3,1,0), Sb(3,0,1,2), Sb(3,0,2,1), Sb(3,1,0,2), Sb(3,1,2,0), Sb(3,2,0,1), Sb(3,2,1,0))
なお 上で kfs(..) は frozen_set を継承して、str(self) method がソート済みのデータを表記するように改良したクラスです。上のようにデータの種類が 10 個を超えてきたとき、ソートされていないと、集合に何が含まれているかの判定が困難になります。sorted(frozen_set(..)) と書いても良いのですが、それでは one-liner で書くときに面倒であり、可読性も下がります。set(..) は set instance が hashable でないため、集合の集合を記述できないので、数学では使い物になりません。
また集合どうしの ∪:union を + 演算子で、∩:meet を * 演算子で書けるようにしてあります。A ⊂ B を A < B で書けるようにしてあります。
*PythonSf/Op one-liners*# A ∪ B の例 kfs(0,1,2) + kfs(1,2,3) =============================== kfs(0, 1, 2, 3) # A ∩ B の例 kfs(0,1,2) * kfs(1,2,3) =============================== kfs(1, 2) # 要素と集合の積 Sb(3,0,2,1) extend([Cy(1,2,3)]) =============================== kfs(Sb(3,0,2,1), Sb(3,1,0,2), Sb(3,2,1,0)) extend([Cy(1,2,3)]) Sb(3,0,2,1) =============================== kfs(Sb(1,0,3,2), Sb(2,0,1,3), Sb(3,0,2,1)) # 左剰余類 N=4; extend([Cy(0,1), Cy(range(N))])/extend([Cy(1,2,3)]) =============================== kfs(Sb(0,1), Sb(1,0), Sb(0,1,3,2), Sb(1,0,3,2), Sb(2,0,1,3), Sb(2,0,3,1), Sb(3,0,1,2), Sb(3,0,2,1)) # A ⊂ B ならば B == A ∪ B の例 N=4; extend([Cy(1,2,3)]) < extend([Cy(0,1), Cy(range(N))])+extend([Cy(1,2,3)]) =============================== True
Sb calss instance による Python object の置換操作
Sb class instance は getitem method を備えた Python インスタンスの置換操作ができます このことは Sb,Cy,extend で記述できる群構造は、別の列データや群・環・体インスタンスを実際に one-liners で手軽に置換操作できることを意味します。代数構造における対称構造を具体的に調べられることを意味します。この置換操作と他の Python instance の組み合わせ可能なことが、一見では単純な Sb, Cy, extend の三つだけで組み尽くせない数学でのおもちゃにできる秘密です。
PythonSf/Op one-liners
# tuple の操作
Sb(1,3,2,0)((10,11,12,13,14,15))
===============================
(13, 10, 12, 11, 14, 15)
# リストの操作
Cy(3,7,5)(range(10))
===============================
[0, 1, 2, 5, 4, 7, 6, 3, 8, 9]
# numpy.ndarray の操作
Cy(3,7,5)(np.arange(10))
===============================
[0 1 2 5 4 7 6 3 8 9]
Sb(1,3,2,0)(np.arange(4*3).reshape(4,3))
===============================
[[ 9 10 11]
[ 0 1 2]
[ 6 7 8]
[ 3 4 5]]
# random な shuffle:入れ替え操作との組み合わせ
seed(0); Sb(1,3,2,0)(shuffle([10,11,12,13,14,15]))
===============================
[13, 15, 11, 12, 10, 14]
\(Sn(3),Sn(4),Sn(5),Sn(6)\)対称群 \(An(3),An(4),An(5),An(6)\)交代群 のファイル変数
なお、PythonSf にはファイル変数の機能があります。カレント・ディレクトリに piclable な Python インスタンスをファイルとして残しておき、=: 演算子で呼び出す機能です。配布している PythonSf には \(Sn(3),Sn(4),Sn(5),Sn(6)\) 対称群、および \(An(3),An(4),An(5),An(6)\) 交代群 のファイル変数が含まれています。ファイル変数名は SS3,SS4,SS5,SS6 および SA3,SA4,SA5,SA6 です。
PythonSf one-liners # Sn(3) 対称群 =: SS3; SS3 =============================== kfs(Sb(0,1,2), Sb(0,2,1), Sb(1,0,2), Sb(1,2,0), Sb(2,0,1), Sb(2,1,0))
# Sn(4) 対称群に対する An(4) 交代群、Sn(3)対称群の左剰余類
=: SS4,SA4,SS3; SS4/SA4, SS4/SS3
===============================
(kfs(Sb(0,1,2,3), Sb(0,1,3,2)),
kfs(Sb(0,1,2,3), Sb(0,1,3,2), Sb(0,2,3,1), Sb(1,2,3,0)))
# Sn(4) の中での Sn(3) の共役類全てを列挙する
=: SS4,SA4,SS3; kfs( p SS3 p^-1 for p in SS4)
===============================
kfs(kfs(Sb(0,1,2,3), Sb(0,1,3,2), Sb(0,2,1,3), Sb(0,2,3,1), Sb(0,3,1,2), Sb(0,3,2,1)),
kfs(Sb(0,1,2,3), Sb(0,2,1,3), Sb(1,0,2,3), Sb(1,2,0,3), Sb(2,0,1,3), Sb(2,1,0,3)),
kfs(Sb(0,1,2,3), Sb(0,1,3,2), Sb(2,1,0,3), Sb(2,1,3,0), Sb(3,1,0,2), Sb(3,1,2,0)),
kfs(Sb(0,1,2,3), Sb(0,3,2,1), Sb(1,0,2,3), Sb(1,3,2,0), Sb(3,0,2,1), Sb(3,1,2,0)))
今のところ =: 演算子を使えるのは commercial 版のみの機能です。commercial 版でも 5 秒のディれーが入るだけで、PythonSf の機能は全て使えるので、興味のあるかたはお試しください。また御自分で pickles ファイルを読み出す関数を実装してやればこれらのファイル変数を扱えるようになるでしょう。
Sb クラスの source
PythonSf では殆どのソースを公開しています。 Sb class のソースも公開しています。また Python は他人のコードでも読みやすい言語です。下手なドキュメントより、ソースを読んだほうが分りやすいことも珍しくありません。Sb クラスのソースは下の source(..) 関数を使った PythonSf one-liner で手軽に見れます。興味のある方は見てやって下さい。他のクラスや関数でも source(..) 関数を活用してやってください。
PythonSf, PyhonSfOp ワンライナー
source(extend)
randi(..): 整数ランダム関数, shuffle 関数
numpy.random には rand:[0,1] の一様分布ランダム関数 randn:正規分布ランダム関数, randint:整数ランダム関数が備わっています。PythonSf では numpy は np の名前で import 済みであり下のように これらの関数を扱えます。
PythonSf commercial/open
seed(0); np.random.randn(3)
===============================
[ 1.76405235 0.40015721 0.97873798]
seed(0); np.random.randint(3,size=[4]), np.random.randint(3,size=[3,4])
===============================
(array([0, 1, 0, 1]),
array([[1, 2, 0, 2],
[0, 0, 0, 2],
[1, 2, 2, 0]]))
でも数学を主な対象とする PythonSf では、np.random を常に書くのは冗長です。これらのランダム関数はグローバル変数にあるべきだと考えます。ですから one-liners は下のようにも書けるようにしてあります。
PythonSf commercial
seed(0); randn(3)
===============================
[ 1.76405235 0.40015721 0.97873798]
---- ClTensor ----
seed(0); randi(3,[4]),randi(3,[3,4])
===============================
(ClTensor([0, 1, 0, 1], dtype=int),
ClTensor([[1, 2, 0, 2],
[0, 0, 0, 2],
[1, 2, 2, 0]], dtype=int))
PythonSf open
seed(0); randn(3)
===============================
[ 1.76405235 0.40015721 0.97873798]
seed(0); randi(3,[4]),randi(3,[3,4])
===============================
(array([0, 1, 0, 1]),
array([[1, 2, 0, 2],
[0, 0, 0, 2],
[1, 2, 2, 0]]))
===============================
[[0 1 0 1]
[1 2 0 2]
[0 0 0 2]]
上で randint(..) の変わりに randi(..) 関数を使っているのは、短く表記するためです。size=… と書く代わりに [3,4] などとシーケンス引数を与えます。無用に冗長な記述は思考のリズムを妨げます。これらを使った記述のほうか ずっと快適なはずです。以下で randi(..) 関数を何度も使います。
なお、PythonSf commercial 版では、これらのラムダム関数の戻り行列は ClTensor インスタンスにしてあり、少し扱いやすくしてあります。Open 版では np.ndarray instance を返しています。
shuffle 関数
シーケンス・データをランダムに入れ替える numpy.random.shuffle 関数も global 変数に格上げしてあります。次のように計算できます。shuffle した結果と引数のタイプを同じにしてくれているのが嬉しいところです。
PythonSf commercial/open
seed(0); shuffle(range(10))
===============================
[2, 8, 4, 9, 1, 6, 7, 3, 0, 5]
seed(0); shuffle(np.array(range(10)))
===============================
[2 8 4 9 1 6 7 3 0 5]
PythonSf commercial
seed(0); shuffle(ClTensor(range(10)))
===============================
[ 2. 8. 4. 9. 1. 6. 7. 3. 0. 5.]
---- ClTensor ----
seed(0); shuffle(~[range(10)])
===============================
[ 2. 8. 4. 9. 1. 6. 7. 3. 0. 5.]
---- ClTensor ----
ClTensor は PythonSf commercial 版での整数・実数・複素数向けの行列・ベクトルクラスです。PythonSf commercial 版では ~[….] の記号表記でも、行列・ベクトルを表せます。そして ClTensor(..) での、その要素はデフォルトでは float にしてあります。整数ではありません。物理や工学での問題に集中して考えているとき、頭の中では実数と整数の区別をしていません。その区別が必要になるのは、プログラム・コードに落とすときです。そのコード vc=~[1,2,3] と書いたときに vc を整数ベクトルにすると vc 要素に浮動小数点を代入したとき整数化されてしまいます。
vc=np.array([1,2,3]); vc[0]=pi; vc
===============================
[3 2 3]
vc=~[1,2,3]; vc[0]=pi; vc
===============================
[ 3.14159265 2. 3. ]
---- ClTensor ----
この誤りは稀にしか やらかさないのですが、逆に稀だからこそ面倒なんです。整数化されてしまっても結果は予測から大きくは違わないので直ぐには誤りに気付けないことが多いからです。何週間にもわたる膨大な計算と考察の蓄積の最初のほうに誤りが入り込んでいて、後で何か変だと気付いたときの大変さは理系の方ならば分ってもらえるでしょう。下手をしたら誤っている箇所を特定するだけで一週間が潰れたりすることもあります。それを何回も繰り返したら、車輪の再発明をしてでも default float の ClTensor を作りあげたくなる気持ちも理解してもらえると思います。
なお ClTensor の優位さは default float だけではありません。下のように積演算子を省略できること、行列とベクトルの積を教科書と同じにできることが見た目以上に思考の効率に影響します。数学・物理・工学の問題を検討しているとき、Python プログラム・コードを書くのではなく、積演算子記号 * を空白だけですませるなど、教科書に近い数式書式での PythonSf 式で書けることの思考蓄積における優位性は多くの方に共感してもらえると思います。
PythonSf open
mt=np.array([[1,2],[3,4]]); vc=np.array([5,6]); np.dot(mt,vc)
===============================
[17 39]
PythonSf commercial
mt=~[[1,2],[3,4]]; vc=[5,6]; mt vc
===============================
[ 17. 39.]
---- ClTensor ----
なか 上の shuffle 関数は本稿での数値実験で多用されます。
\(Zp(N)\): Z2,Z3,Z3,Z4,Z5,Z6,Z7, Zb:Z127
配布している PythohSf の sfCrrntIni には 2,3,4,5,6,7,127 整数に対する剰余体・剰余環 Z2,Z3,Z3,Z4,Z5,Z6,Z7, Zb を実装してあります。これらを使った 八元数や多項式を扱えるようにするためです。 これらは加減乗除と整数べき乗算が可能です。下のような具合です
PythonSf commercial/open
[Z3(k) for k in range(6)]
===============================
[0, 1, 2, 0, 1, 2]
[Z5(k)^2 for k in range(6)]
===============================
[0, 1, 4, 4, 1, 0]
[Z5(k)^2 + 1 for k in range(6)]
===============================
[1, 2, 0, 0, 2, 1]
[(Z5(k)^2 + 1)/Z5(3) for k in range(6)]
===============================
[2, 4, 0, 0, 4, 2]
有限体八元数: O2,O3,O3,O4,O5,O6,O7, Ob:O127
Z2,Z3,Z3,Z4,Z5,Z6,Z7, Zb を使った有限体八元数: O2,O3,O3,O4,O5,O6,O7, Ob も PythonSf を配布しているファイルの sfCrrnitIni.py ファイルに定義してあります。八元数が定義してあるということは有限体四元数・有限体複素数も使えることを意味します。実数の八元数は Oc の名前で扱えます。
有限体八元数は、元々は圏論での具体例を one-liners で簡単に記述できるようにする目的で導入したのですが、意外と多方面で有用な代数系です。下にその理由を列挙しておきます。
- 有限ですから、虱潰し方による brute force な証明が簡単にできる。
- 有限体複素数・有限体四元数・有限体複素数 × Z2,Z3,Z3,Z4,Z5,Z6,Z7, Zb と多数の代数系が得られる
- 非可換環だけでなく、加減乗除算はできても結合律さえなりたたない環とも言えない八元数代数系がえられ、Galois 理論など通常では体しか考えられていない代数系の性質を非可換環や八元数体などに拡張したときの様子を実験できる。境界例を実際に作れる
- 適度に複雑な代数系であり、予測しきれない性質を見せてくれる
- Sb(..) 置換インスタンスを使って有限体八元数を置換できる。代数系を振り回して その対称性を調べられる。
八元数の conjugate と norm と積演算における norm の保存 逆元の有無
実数四元数、八元数でも norm を定義できます。それを有限体八元数にも援用できます。実数八元数の積は norm を保存します。この性質は有限体八元数でも成り立ちます。また有限体八元数の norm が 0 でないことと逆元の有無は同値です。
実数複素数と同様に、四元数・八元数に対して その conjugate が考えられます。conjugate 値は、非実数部分の符号が反転させた物であり、.d 属性で得られます。下のような具合です。
PythonSf commercial/open
seed(0); a,b,c = Oc(randn(2)), Oc(randn(4)), Oc(randn(8)); a,b,c
===============================
(Oc(1.764052345967664, 0.40015720836722329),
Oc(0.9787379841057392, 2.2408931992014578, 1.8675579901499675, -0.97727787987641102),
Oc(0.95008841752558937, -0.15135720829769789, -0.10321885179355784, 0.41059850193837233, 0.14404357116087799, 1.4542735069629751, 0.76103772514699342, 0.12167501649282841))
seed(0); a,b,c = Oc(randn(2)), Oc(randn(4)), Oc(randn(8)); a.d, b.d, c.d
===============================
(Oc(1.764052345967664, -0.40015720836722329),
Oc(0.9787379841057392, -2.2408931992014578, -1.8675579901499675, 0.97727787987641102),
Oc(0.95008841752558937, 0.15135720829769789, 0.10321885179355784, -0.41059850193837233, -0.14404357116087799, -1.4542735069629751, -0.76103772514699342, -0.12167501649282841))
複素数の場合のときと同様に、四元数・八元数も conjugate 値との積は正値となり、norm 長を定義できます。(下の norm の自乗の計算例で 実数値成分以外にも非ゼロ成分が出てきますが、これはコンピュータの float 計算における計算誤差です。64bit double 実数は 17 桁程度の精度ですから、それに近い誤差は実数値を扱う限り付きまといます。)
PythonSf commercial/open
seed(0); a,b,c = Oc(randn(2)), Oc(randn(4)), Oc(randn(8)); a*a.d, b*b.d, c*c.d
===============================
(Oc(3.27200647072),
Oc(10.422375272827431, 0.0, 0.0, 1.1102230246251565e-16),
Oc(3.8344654789621773, 0.0, 0.0, 9.0205620750793969e-17, 6.9388939039072284e-18, -8.5001450322863548e-17, -2.7755575615628914e-17, 1.3877787807814457e-17))
seed(0); a,b,c = (randn(2)), (randn(4)), (randn(8)); norm(a)^2, norm(b)^2, norm(c)^2
===============================
(3.2720064707222685, 10.42237527282743, 3.834465478962177)
複素数・四元数・八元数の norm には「積演算で norm が保たれる」\(\) の性質があります。
PythonSf commercial/open
seed(0); a0,a1 = [Oc(x) for x in randn(2,2)]; b0,b1=[Oc(x) for x in randn(2,4)]; c0,c1=[Oc(x) for x in randn(2,8)]; (a0*a1)*(a0*a1).d - (a0*a0.d)*(a1*a1.d), (b0*b1)*(b0*b1).d - (b0*b0.d)*(b1*b1.d), (c0*c1)*(c0*c1).d - (c0*c0.d)*(c1*c1.d)
===============================
(Oc(3.5527136788e-15),
Oc(1.7763568394002505e-15, 0.0, 6.4251527559699568e-17, 3.4961505313766965e-17),
Oc(7.1054273576010019e-15, -4.3140830754274083e-32, -8.6303910305240338e-16, -4.4408920985006262e-16, -1.9485879348156088e-15, -1.3336630009075002e-15, 1.5975444297487229e-15, -8.8910866727166678e-16))
逆に積演算で norm を保つ実数の拡張は複素数・四元数・八元数に限られることを Frobenius が証明しています。
さて、有限体複素数・四元数・八元数: O2,O3,O3,O4,O5,O6,O7, Ob でも、この積演算と norm の関係は継承されます。有限体複素数・四元数・八元数では、その conjugate との積は Z2,Z3,Z3,Z4,Z5,Z6,Z7, Zb の値になります。次のように数値実験で正しそうなのが確認できます。
PythonSf commercial/open
seed(0); a,b,c = O5(randi(5,[2])), O5(randi(5,[4])), O5(randi(5,[8])); a*a.d, b*b.d, c*c.d
===============================
(O5(Z5(1)), O5(Z5(3)), O5(Z5(0)))
「積演算で norm を保つ」性質も成り立ちます。ただし Z2,Z3,Z3,Z4,Z5,Z6,Z7, Zb では自乗根が存在しないときもあるので、厳密には「norm の自乗:conjugate との積が、積演算でも保たれる」\(\) となります。次のように PythonSf one-liner で数値実験できます。
PythonSf commercial/open
seed(0); a0,a1 = [O5(x) for x in randi(5,[2,2])]; b0,b1=[O5(x) for x in randi(5,[2,4])]; c0,c1=[O5(x) for x in randi(5,[2,8])]; (a0*a1)*(a0*a1).d - (a0*a0.d)*(a1*a1.d), (b0*b1)*(b0*b1).d - (b0*b0.d)*(b1*b1.d), (c0*c1)*(c0*c1).d - (c0*c0.d)*(c1*c1.d)
===============================
(O5(Z5(0)), O5(Z5(0)), O5(Z5(0)))
seed(0); a0,a1 = [O5(x) for x in randi(5,[2,2])]; b0,b1=[O5(x) for x in randi(5,[2,4])]; c0,c1=[O5(x) for x in randi(5,[2,8])]; (a0*a1)*(a0*a1).d == (a0*a0.d)*(a1*a1.d), (b0*b1)*(b0*b1).d == (b0*b0.d)*(b1*b1.d), (c0*c1)*(c0*c1).d == (c0*c0.d)*(c1*c1.d)
===============================
(True, True, True)
有限体八元数で norm(..)^2 が 0 になると逆元が存在しなくなります。\(x x.d == normSq\) ならば \(x x.d/normSq == 1\) であり、 \(x^-1 == x.d/normSq\) だからです。
O2,O3,O4,O5,O6,O7,Ob 複素数・四元数・八元数の性質
O2,O3,O4,O5,O6,O7,Ob 複素数・四元数・八元数には、下のような代数的な性質があります。
- O3,O7,Ob 複素数 は可換有限体になります
- O2,O4,O5,O6 複素数は可換環になります。O2,O5 複素数は体にはなれません。
- O3,O4,O5,O6,O7,Ob 四元数は非可換環になります
- O3,O4,O5,O6,O7,Ob 八元数は結合律も成り立たなくなるので、非可換環にもなれません
- O2 複素数・四元数・八元数は可換環になります。
O2 O5 複素数が可換体になれないのは、2 と 5 が素数だけに変な気がするかもしれませんが、下のように normの自乗が 0 になるものがあることより証明できます。
PythonSf commercial/open
O2(1,1)*O2(1,1).d, O5(1,2)*O5(1,2).d
===============================
(O2(Z2(0)), O5(Z5(0)))
以上で本稿で使う道具立ての説明が終わりました。次の章では Sb 置換群の使い方の手始めに D6 二面体群における Sylow 群を検討してみます。 その次の章では、Sb 置換群に伴う八元数を調べてみます。
D6 六面体群における Shylow の定理の適用
シローの定理とはここの wikipedia の説明 にあるようなものです。下に この wikipedia の説明を再掲します
それぞれなんらかの意味で極大な部分群の集まりというのは群論においてよくある。ここで驚くべき結果は、\(Syl_p(G)\) の場合には、すべての元が実は互いに同型で、可能な最大の位数を持っているということである:\(|G| = p^n\ m, n > 0\) で、\(p\) が \(m\) を割り切らなければ、任意のシロー\(p-\)部分群\(P\)の位数は \(|P| = p^n\) である。つまり、\(P\)は \(p-\)群であり\(gcd(|G : P|, p) = 1\) である。これらの性質は\(G\)の構造をさらに分析するために利用することができる。
- 定理1: 有限群\(G\)の位数の任意の素因数\(p\)(重複度 n)に対し、位数 \(p^n\) の G のシロー\(p\)部分群が存在する。
- 定理1の次の弱いバージョンは最初コーシーによって証明され、コーシーの定理として知られている。
- 系: 有限群\(G\)と\(G\)の位数を割り切る素数\(p\)が与えられると、\(G\)には位数\(p\)の元(したがって位数\(p\)の部分群)が存在する。
- 定理2: 有限群\(G\)と素数\(p\)が与えられると、\(G\)のすべてのシロー\(p-\)部分群は互いに共役である、つまり、\(H\)と\(K\)が\(G\)のシロー\(p-\)部分群であれば、\(g^{-1} H g = K\)なる\(G\)の元\(g\)が存在する。
- 定理3:\(p\)を有限群\(G\)の位数の素因数で重複度を\(n\)とする。よって\(G\)の位数は\(p^n m\)と書ける、ただし\(n > 0\)であり\(p\)は\(m\)を割らない。\(n_p\)を\(G\)のシロー\(p-\)部分群の個数とする。すると次が成り立つ:
- \(n_p\) は\(G\)のシロー\(p\)部分群の指数である\(m\)を割り切る。
- \(n_p\ \equiv\ 1\ mod\ p\).
- \(n_p = |G : NG(P)|\), ここで\(P\)は\(G\)の任意のシロー\(p-\)部分群であり\(NG\)は正規化群を表す。
そして二面体群について次のように説明してくれます。
シロー部分群とシローの定理の簡単な実例はn角形の二面体群Dnである。nが偶数の場合、群の位数は4で割り切れるため、鏡映によって生成される群はシロー部分群にはならず、2種類の共役類に分解される。幾何学的にはその対称軸が2辺を通るか2頂点を通るかによってどちらの共役類に属するかが決まる。これは外部自己同型と関係しており、π/nラジアンの回転(二面体群の最小の回転の半分)によって表現される。
\(D_6\)においては鏡映はシロー\(2-\)部分群に対応せず、2種類の共役類に分類される。
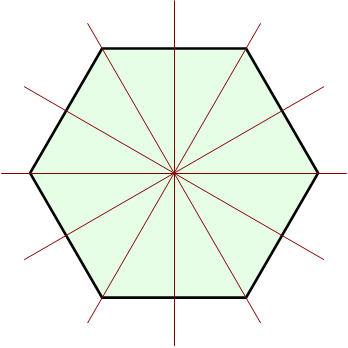
でも、こんな説明だけで分る方は数少ないでしょう。Sb 置換群を使って、この六面体群 D6 の例をより詳しく見ていきましょう。
六角形の頂点に 0,1,2,3,4,5 の番号を割り振ると S0,S1,S2,S3,S4,S5 鏡映対称をを置換群で表現できます。
2 1
3 0
4 5
S0,S1,S2 = Sb(0,5,4,3,2,1),Sb(2,1,0,5,4,3),Sb(4,3,2,1,0,5) は (0,3),(1,4),(2,5) の頂点を結ぶ線に対し折り返し対称な置換変換です。
S3,S4,S5 = Sb(1,0,5,4,3,2),Sb(3,2,1,0,5,4),Sb(5,4,3,2,1,0) のうち S3は [(0,1),(3,4)] の二組の変の中天を結ぶ線に対し折り返し対称な置換変換です。S2,S3 も同様に、二組の変の中天を結ぶ線に対し折り返し対称な置換変換です。これらの置換を含む最小の群を extend(..) 関数で作れます。
PythonSf commercial/open
S0,S1,S2,S3,S4,S5 = Sb(0,5,4,3,2,1),Sb(2,1,0,5,4,3),Sb(4,3,2,1,0,5),Sb(1,0,5,4,3,2),Sb(3,2,1,0,5,4),Sb(5,4,3,2,1,0); extend([S0,S1,S2,S3,S4,S5])
===============================
kfs(Sb(0,1,2,3,4,5), Sb(0,5,4,3,2,1), Sb(1,0,5,4,3,2), Sb(1,2,3,4,5,0), Sb(2,1,0,5,4,3), Sb(2,3,4,5,0,1), Sb(3,2,1,0,5,4), Sb(3,4,5,0,1,2), Sb(4,3,2,1,0,5), Sb(4,5,0,1,2,3), Sb(5,0,1,2,3,4), Sb(5,4,3,2,1,0))
S0,S1,S2,S3,S4,S5 の鏡映変換の集合にはなかった位数 6 の巡回群構造が extend([S0,S1,S2,S3,S4,S5]) の群に入り込んできています。巡回置換が Sb(1,2,3,4,5,0) が extend([S0,S1,S2,S3,S4,S5]) に含まれています。
S0,S1,S2,S3,S4,S5 = Sb(0,5,4,3,2,1),Sb(2,1,0,5,4,3),Sb(4,3,2,1,0,5),Sb(1,0,5,4,3,2),Sb(3,2,1,0,5,4),Sb(5,4,3,2,1,0); Sb(1,2,3,4,5,0) in extend([S0,S1,S2,S3,S4,S5]) =============================== True
σ=Sb(1,2,3,4,5,0)∈D6 ならば {σ^0,… σ^5} ⊂ D6 です。
PythonSf commercial/open
S0,S1,S2,S3,S4,S5 = Sb(0,5,4,3,2,1),Sb(2,1,0,5,4,3),Sb(4,3,2,1,0,5),Sb(1,0,5,4,3,2),Sb(3,2,1,0,5,4),Sb(5,4,3,2,1,0); σ=Sb(1,2,3,4,5,0); kfs(σ^k for k in range(6)) < extend([S0,S1,S2,S3,S4,S5])
===============================
True
S0,S1,S2,S3,S4,S5 = Sb(0,5,4,3,2,1),Sb(2,1,0,5,4,3),Sb(4,3,2,1,0,5),Sb(1,0,5,4,3,2),Sb(3,2,1,0,5,4),Sb(5,4,3,2,1,0); σ=Sb(1,2,3,4,5,0); extend(σ) < extend([S0,S1,S2,S3,S4,S5])
===============================
True
六面体群 D6:extend([S0,S1,S2,S3,S4,S5]) の位数は 12==2^2*3 です。以下では (Syl_2(D6)\) すなわち シロー\(2-\)部分群の集合を構築し、その性質を調べてみます。
PythonSf commercial/open
S0,S1,S2,S3,S4,S5 = Sb(0,5,4,3,2,1),Sb(2,1,0,5,4,3),Sb(4,3,2,1,0,5),Sb(1,0,5,4,3,2),Sb(3,2,1,0,5,4),Sb(5,4,3,2,1,0); extend([S0,S1,S2,S3,S4,S5]).__len__()
===============================
12
2^2 Sylow 群
\(12 = |D6| = 2^2\ 3\) で、\(2\) が \(3\) を割り切らないので、任意のシロー\(2-\)部分群\(P\)の位数は \(|P| = 2^2\) です。 ならば、D6 六面体群全体より、全ての 2 個の置換を取り出し、それが作る群の位数が四になるものを全て列挙してみましょう。下のようになります。
PythonSf commercial/open
S0,S1,S2,S3,S4,S5 = Sb(0,5,4,3,2,1),Sb(2,1,0,5,4,3),Sb(4,3,2,1,0,5),Sb(1,0,5,4,3,2),Sb(3,2,1,0,5,4),Sb(5,4,3,2,1,0); ls=[S0,S1,S2,S3,S4,S5]; kfs( Bf.x for pair in tn.it.combinations(extend(ls),2) if (Bf(x=extend(pair)), Bf.x.__len__() == 4)[-1])
===============================
kfs(kfs(Sb(0,1,2,3,4,5), Sb(0,5,4,3,2,1), Sb(3,2,1,0,5,4), Sb(3,4,5,0,1,2)),
kfs(Sb(0,1,2,3,4,5), Sb(1,0,5,4,3,2), Sb(3,4,5,0,1,2), Sb(4,3,2,1,0,5)),
kfs(Sb(0,1,2,3,4,5), Sb(2,1,0,5,4,3), Sb(3,4,5,0,1,2), Sb(5,4,3,2,1,0)))
上で (Bf(x=extend(pair)), Bf.x.__len__() == 4)[-1] と一見見慣れない tuple 式を使いました。ここで使った Bf(..) は、 Python では comprehension 構文で local 変数を使えないのをどうしても使えるようにしたくて導入したクラスインスタンスです。キーワード引数を使って Bf.x テンポラリ変数に に extend(pair) の計算結果を残しています。Lisp での (progn E0 E1 E2 ...) のような記述を可能にします。tuple の最後の式値が true のときの結果だけを残したいので [-1] の項が入っています。綺麗ではないのは分っていますが、醜さを承知の上で導入したくなるだけの魅力が PythohSf one-liners にあります。数少ない PythonSf の Bad knowhow だと思ってやってください。
定理が主張しているように \(Syl_2(D6)\) は三つの部分群になりました。それぞれの部分群の各要素を全部調べてみましょう。単位元を除いて全ての位数が 2 です。4 のものもあるかと思ったのですが、ありませんでした。でも これで \(Syl_2(D6)\) が 2-群であることは確認できました。
PythonSf commercial/open
[kfs(σ^k for k in range(6)).__len__() for σ in kfs(Sb(0,1,2,3,4,5), Sb(0,5,4,3,2,1), Sb(3,2,1,0,5,4), Sb(3,4,5,0,1,2)).sl]
===============================
[1, 2, 2, 2]
[kfs(σ^k for k in range(6)).__len__() for σ in kfs(Sb(0,1,2,3,4,5), Sb(1,0,5,4,3,2), Sb(3,4,5,0,1,2), Sb(4,3,2,1,0,5)).sl]
===============================
[1, 2, 2, 2]
[kfs(σ^k for k in range(6)).__len__() for σ in kfs(Sb(0,1,2,3,4,5), Sb(2,1,0,5,4,3), Sb(3,4,5,0,1,2), Sb(5,4,3,2,1,0)).sl]
===============================
[1, 2, 2, 2]
ちなみに D6 六面体群の正規部分群は位数 3 の下のように小さなものです。
PythonSf commercial/open
S0,S1,S2,S3,S4,S5 = Sb(0,5,4,3,2,1),Sb(2,1,0,5,4,3),Sb(4,3,2,1,0,5),Sb(1,0,5,4,3,2),Sb(3,2,1,0,5,4),Sb(5,4,3,2,1,0); σ=Sb(1,2,3,4,5,0); ls=extend([S0,S1,S2,S3,S4,S5]); kfs(x*y*x^-1*y^-1 for x,y in mitr(ls,ls))
===============================
kfs(Sb(0,1,2,3,4,5), Sb(2,3,4,5,0,1), Sb(4,5,0,1,2,3))
共役変換
PythonSf commercial
上の \(Syl_2(D6)\) の三つの同型な 2-群の間を遷移させる共役類を全て列挙してみした。何らかの規則性があるかもと思ったからです。なんか規則性はあるようですが、明確にできません。明確な規則性を説明できる方がいたら教えてやってください。
kfs(Sb(0,1,2,3,4,5), Sb(0,5,4,3,2,1), Sb(3,2,1,0,5,4), Sb(3,4,5,0,1,2)) をkfs(Sb(0,1,2,3,4,5), Sb(1,0,5,4,3,2), Sb(3,4,5,0,1,2), Sb(4,3,2,1,0,5)) に移す共役変換を全て列挙してみます。
kfa, kfb,kfc = kfs(Sb(0,1,2,3,4,5), Sb(0,5,4,3,2,1), Sb(3,2,1,0,5,4), Sb(3,4,5,0,1,2)), kfs(Sb(0,1,2,3,4,5), Sb(1,0,5,4,3,2), Sb(3,4,5,0,1,2), Sb(4,3,2,1,0,5)), kfs(Sb(0,1,2,3,4,5), Sb(2,1,0,5,4,3), Sb(3,4,5,0,1,2), Sb(5,4,3,2,1,0)); S0,S1,S2,S3,S4,S5 = Sb(0,5,4,3,2,1),Sb(2,1,0,5,4,3),Sb(4,3,2,1,0,5),Sb(1,0,5,4,3,2),Sb(3,2,1,0,5,4),Sb(5,4,3,2,1,0); ls=extend([S0,S1,S2,S3,S4,S5]); [p for p in ls if p*kfa*p^-1 == kfb]
===============================
[Sb(2,1,0,5,4,3), Sb(2,3,4,5,0,1), Sb(5,0,1,2,3,4), Sb(5,4,3,2,1,0)]
kfa, kfb,kfc = kfs(Sb(0,1,2,3,4,5), Sb(0,5,4,3,2,1), Sb(3,2,1,0,5,4), Sb(3,4,5,0,1,2)), kfs(Sb(0,1,2,3,4,5), Sb(1,0,5,4,3,2), Sb(3,4,5,0,1,2), Sb(4,3,2,1,0,5)), kfs(Sb(0,1,2,3,4,5), Sb(2,1,0,5,4,3), Sb(3,4,5,0,1,2), Sb(5,4,3,2,1,0)); S0,S1,S2,S3,S4,S5 = Sb(0,5,4,3,2,1),Sb(2,1,0,5,4,3),Sb(4,3,2,1,0,5),Sb(1,0,5,4,3,2),Sb(3,2,1,0,5,4),Sb(5,4,3,2,1,0); ls=extend([S0,S1,S2,S3,S4,S5]); [p for p in ls if p*kfb*p^-1 == kfc]
===============================
[Sb(2,3,4,5,0,1), Sb(5,0,1,2,3,4), Sb(0,5,4,3,2,1), Sb(3,2,1,0,5,4)]
kfa, kfb,kfc = kfs(Sb(0,1,2,3,4,5), Sb(0,5,4,3,2,1), Sb(3,2,1,0,5,4), Sb(3,4,5,0,1,2)), kfs(Sb(0,1,2,3,4,5), Sb(1,0,5,4,3,2), Sb(3,4,5,0,1,2), Sb(4,3,2,1,0,5)), kfs(Sb(0,1,2,3,4,5), Sb(2,1,0,5,4,3), Sb(3,4,5,0,1,2), Sb(5,4,3,2,1,0)); S0,S1,S2,S3,S4,S5 = Sb(0,5,4,3,2,1),Sb(2,1,0,5,4,3),Sb(4,3,2,1,0,5),Sb(1,0,5,4,3,2),Sb(3,2,1,0,5,4),Sb(5,4,3,2,1,0); ls=extend([S0,S1,S2,S3,S4,S5]); [p for p in ls if p*kfc*p^-1 == kfa]
===============================
[Sb(2,3,4,5,0,1), Sb(5,0,1,2,3,4), Sb(1,0,5,4,3,2), Sb(4,3,2,1,0,5)]
[Sb(2,3,4,5,0,1) Sb(2,1,0,5,4,3), Sb(5,0,1,2,3,4) Sb(2,3,4,5,0,1), Sb(0,5,4,3,2,1) Sb(5,0,1,2,3,4), Sb(3,2,1,0,5,4) Sb(5,4,3,2,1,0)]
===============================
[Sb(4,3,2,1,0,5), Sb(1,2,3,4,5,0), Sb(1,0,5,4,3,2), Sb(4,5,0,1,2,3)]
[Sb(5,0,1,2,3,4) Sb(2,1,0,5,4,3), Sb(2,3,4,5,0,1) Sb(2,3,4,5,0,1), Sb(0,5,4,3,2,1) Sb(5,0,1,2,3,4), Sb(3,2,1,0,5,4) Sb(5,4,3,2,1,0)]
===============================
[Sb(1,0,5,4,3,2), Sb(4,5,0,1,2,3), Sb(1,0,5,4,3,2), Sb(4,5,0,1,2,3)]
\(Syl_2(D6)\) の正規化群
\(Syl_2(D6)\) の三つの 2-群 を kfa,kfb,kfc と名づけて、それの正規化群がやはり kfa,kfb,kfc であることを確認しました。\(n_p\)を\(G\)のシロー\(p-\)部分群の個数とする。すると \(n_p = |G : NG(P)|\) が成り立つことを確認できました。
PythonSf commercial
kfa, kfb,kfc = kfs(Sb(0,1,2,3,4,5), Sb(0,5,4,3,2,1), Sb(3,2,1,0,5,4), Sb(3,4,5,0,1,2)), kfs(Sb(0,1,2,3,4,5), Sb(1,0,5,4,3,2), Sb(3,4,5,0,1,2), Sb(4,3,2,1,0,5)), kfs(Sb(0,1,2,3,4,5), Sb(2,1,0,5,4,3), Sb(3,4,5,0,1,2), Sb(5,4,3,2,1,0)); kfs(x y x^-1 y^-1 for x,y in mitr(kfa,kfa))
kfa, kfb,kfc = kfs(Sb(0,1,2,3,4,5), Sb(0,5,4,3,2,1), Sb(3,2,1,0,5,4), Sb(3,4,5,0,1,2)), kfs(Sb(0,1,2,3,4,5), Sb(1,0,5,4,3,2), Sb(3,4,5,0,1,2), Sb(4,3,2,1,0,5)), kfs(Sb(0,1,2,3,4,5), Sb(2,1,0,5,4,3), Sb(3,4,5,0,1,2), Sb(5,4,3,2,1,0)); S0,S1,S2,S3,S4,S5 = Sb(0,5,4,3,2,1),Sb(2,1,0,5,4,3),Sb(4,3,2,1,0,5),Sb(1,0,5,4,3,2),Sb(3,2,1,0,5,4),Sb(5,4,3,2,1,0); ls=extend([S0,S1,S2,S3,S4,S5]); kfs(g for g in ls if g kfa == kfa g)
===============================
kfs(Sb(0,1,2,3,4,5), Sb(0,5,4,3,2,1), Sb(3,2,1,0,5,4), Sb(3,4,5,0,1,2))
kfa, kfb,kfc = kfs(Sb(0,1,2,3,4,5), Sb(0,5,4,3,2,1), Sb(3,2,1,0,5,4), Sb(3,4,5,0,1,2)), kfs(Sb(0,1,2,3,4,5), Sb(1,0,5,4,3,2), Sb(3,4,5,0,1,2), Sb(4,3,2,1,0,5)), kfs(Sb(0,1,2,3,4,5), Sb(2,1,0,5,4,3), Sb(3,4,5,0,1,2), Sb(5,4,3,2,1,0)); S0,S1,S2,S3,S4,S5 = Sb(0,5,4,3,2,1),Sb(2,1,0,5,4,3),Sb(4,3,2,1,0,5),Sb(1,0,5,4,3,2),Sb(3,2,1,0,5,4),Sb(5,4,3,2,1,0); ls=extend([S0,S1,S2,S3,S4,S5]); kfs(g for g in ls if g kfa == kfa g) == kfa
===============================
True
私は \(NG(P)\) を P の正規部分群のことと誤解していました。でも \(P\) の正規部分群は下のように単なる単位元でした。ここで初めて \(NG(P)\) は正規化群のことであり、正規部分群のことではないと気付きました。
PythonSf commercial
kfa = kfs(Sb(0,1,2,3,4,5), Sb(0,5,4,3,2,1), Sb(3,2,1,0,5,4), Sb(3,4,5,0,1,2)); kfs(x y x^-1 y^-1 for x,y in mitr(kfa, kfa))
===============================
kfs(Sb(0,1,2,3,4,5))
シローの定理は、ここで行ったような規模の複雑さを持った群で数例定理がなりたつことを確認してみないと、定理の意味自体を理解できない、または誤解してしまうような複雑さをもった定理です。最初に示した wikipedia の記事を幾ら読み返してみても、その意味していることを理解できないと思います。
GAP と PythonSf Sb,Cy,extend(..) の比較
GAP は群論計算を行うために開発された素晴らしいソフトです。Sb,Cy,extend(..) の組み合わせだけでは不可能な高度な計算が可能です。
でも逆に高度すぎて GAP を使いこなせる方は限られてしまいます。ここでのよう Sb,Cy,extend(..) の三つだけならば、学習コストは限りなくゼロに近いといえます。Python を知っていれば 1 時間もかからずに、今までの記事を読んだだけで、自分の問題に Sb,Cy,exntend(..) を使い出せるはずです。
さらに Python には kfs 集合や iterator, comprehension といった置換の集まりの取り扱いを容易にする機能が備わっています。ここで示したように置換群の集合が作る部分群を求めたり、共役類による変換や正規部分群・正規化部分群を作ったりする操作が one-liners で記述できてしまいます。この章での D6 六面体群における Sylow 2-群の取り扱いなど GAP で再現する気にはなれないと思います。如何でしょうか。
有限体八元数の群操作による代数系の対称構造: Galois の基本定理
この章では、有限体八元数を \(Sn(8)\) 対称群の置換操作でぶん回し、Galois の基本定理:部分体の対称構造と部分群の構造の対応の具体例を見ていきます。
ここで体の置換 σ による ぶん回しによる体 \(F\)の対称構造とは、次のように積演算と和演算が保たれることを意味します。
私は上の和・積演算が置換演算によって保たれることに、幾何学の合同操作のイメージを対応させています。積と和の演算が置換操作によって保たれるのは、合同操作によって辺の長さと角度が保たれることと対応させています。たぶん Galois も同様なイメージを持っていたはずだと思います。Galois は群と動じに 有理数に根を追加した \(Q(r_1,r_2, .. r_n)\) の群によるぶん回しによる対称性も同時に考え出したのですから。群だけを単独で考え出したのではないのですから。また \(Sn(N)\) のことを対称群:symmetric group と呼ぶのも、そのような幾何学的なイメージを伴っていたからだろうと思っています。
Galois の基本定理
ここにある Galois の基本定理 を下に再掲します。
\(Gal(E/F)\) の任意の部分群 \(H\)に対し、対応する体は普通 \(E^H\) と書き、全ての \(H\) の自己同型により固定される \(E\) の元の集合である。
以下 \(F\) として O3(0),O3(1),O3(2):O3 八元数実数と考え、\(E\) として O3 八元数全体を考えます。この \(F\) \(E\) に対し具体的に部分群 \(H\) を構成し、この置換に対して不変な \(E^H\) 部分体を構築します。
O3 八元数の \(Sn(8)\) による対称性
\(Sn(8)\) 対称群の要素のうち O3 八元数に対して合同:対称な:和と積演算を保存する変換を抜き出します。全ての O3 八元数に対して積が保存するものを \(Sn(8)\) の要素から絞り出します。\(Sn(8)\) は range(8) を permutate したものから Sb を作ることで実装してやります。搾り出した \(Sn(8)\) 要素にたいして σ(x y) == σ(x) σ(y) が成り立つことを全ての O3 八元数 x,y について行います。なお以下では * 演算子を省略した PythonSf Commerciala 版のみで記述していきます。 PythonSf Open 版で計算するときは * 演算子を補ってください。
PythonSf commercial
N=10; seed(0); lss=[(O3(randi(3,[8])),O3(randi(3,[8]))) for _ in range(N)]; ls=range(8); [Bf.σ for vσ in permutate(ls) if (Bf(σ=Sb(vσ)), all( Bf.σ(x) Bf.σ(y) == Bf.σ(x y) for x,y in lss))[-1]]
===============================
[Sb(0,1,2,3,4,5,6,7), Sb(0,1,4,5,7,6,3,2), Sb(0,1,7,6,2,3,5,4), Sb(0,2,3,1,4,6,7
,5), Sb(0,2,4,6,5,7,1,3), Sb(0,2,5,7,3,1,6,4), Sb(0,3,1,2,4,7,5,6), Sb(0,3,4,7,6
,5,2,1), Sb(0,3,6,5,1,2,7,4), Sb(0,4,5,1,7,3,2,6), Sb(0,4,6,2,5,1,3,7), Sb(0,4,7
,3,6,2,1,5), Sb(0,5,1,4,7,2,6,3), Sb(0,5,3,6,1,4,2,7), Sb(0,5,7,2,3,6,4,1), Sb(0
,6,1,7,2,4,3,5), Sb(0,6,2,4,5,3,7,1), Sb(0,6,5,3,1,7,4,2), Sb(0,7,2,5,3,4,1,6),
Sb(0,7,3,4,6,1,5,2), Sb(0,7,6,1,2,5,4,3)]
lsSb=[Sb(0,1,2,3,4,5,6,7), Sb(0,1,4,5,7,6,3,2), Sb(0,1,7,6,2,3,5,4), Sb(0,2,3,1,4,6,7 ,5), Sb(0,2,4,6,5,7,1,3), Sb(0,2,5,7,3,1,6,4), Sb(0,3,1,2,4,7,5,6), Sb(0,3,4,7,6 ,5,2,1), Sb(0,3,6,5,1,2,7,4), Sb(0,4,5,1,7,3,2,6), Sb(0,4,6,2,5,1,3,7), Sb(0,4,7 ,3,6,2,1,5), Sb(0,5,1,4,7,2,6,3), Sb(0,5,3,6,1,4,2,7), Sb(0,5,7,2,3,6,4,1), Sb(0 ,6,1,7,2,4,3,5), Sb(0,6,2,4,5,3,7,1), Sb(0,6,5,3,1,7,4,2), Sb(0,7,2,5,3,4,1,6), Sb(0,7,3,4,6,1,5,2), Sb(0,7,6,1,2,5,4,3)]; lsO3=list(O3(vc) for vc in mitr(*[range(3)]*8)); [all( σ(x y) == σ(x) σ(y) for x,y in mitr(lsO3,lsO3)) for σ in lsSb]
time:10:29
正規部分群を作る
上で求めた O3 八元数の対称性を保つ変換の集合がグループとして閉じていることを確認します。
PythonSf commercial
ls=[Sb(0,1,2,3,4,5,6,7), Sb(0,1,4,5,7,6,3,2), Sb(0,1,7,6,2,3,5,4), Sb(0,2,3,1,4,6,7 ,5), Sb(0,2,4,6,5,7,1,3), Sb(0,2,5,7,3,1,6,4), Sb(0,3,1,2,4,7,5,6), Sb(0,3,4,7,6 ,5,2,1), Sb(0,3,6,5,1,2,7,4), Sb(0,4,5,1,7,3,2,6), Sb(0,4,6,2,5,1,3,7), Sb(0,4,7 ,3,6,2,1,5), Sb(0,5,1,4,7,2,6,3), Sb(0,5,3,6,1,4,2,7), Sb(0,5,7,2,3,6,4,1), Sb(0 ,6,1,7,2,4,3,5), Sb(0,6,2,4,5,3,7,1), Sb(0,6,5,3,1,7,4,2), Sb(0,7,2,5,3,4,1,6), Sb(0,7,3,4,6,1,5,2), Sb(0,7,6,1,2,5,4,3)]; all( x y in ls for x,y in mitr(ls,ls))
===============================
True
この部分群の暗い数は 21 です。部分群として異数が 7 のものと 3 のものがあるはずです。
PythonSf commercial
ls=[Sb(0,1,2,3,4,5,6,7), Sb(0,1,4,5,7,6,3,2), Sb(0,1,7,6,2,3,5,4), Sb(0,2,3,1,4,6,7 ,5), Sb(0,2,4,6,5,7,1,3), Sb(0,2,5,7,3,1,6,4), Sb(0,3,1,2,4,7,5,6), Sb(0,3,4,7,6 ,5,2,1), Sb(0,3,6,5,1,2,7,4), Sb(0,4,5,1,7,3,2,6), Sb(0,4,6,2,5,1,3,7), Sb(0,4,7 ,3,6,2,1,5), Sb(0,5,1,4,7,2,6,3), Sb(0,5,3,6,1,4,2,7), Sb(0,5,7,2,3,6,4,1), Sb(0 ,6,1,7,2,4,3,5), Sb(0,6,2,4,5,3,7,1), Sb(0,6,5,3,1,7,4,2), Sb(0,7,2,5,3,4,1,6), Sb(0,7,3,4,6,1,5,2), Sb(0,7,6,1,2,5,4,3)]; len(ls)
===============================
21
この部分群の正規部分群を作ってみます。位数が素数の群は巡回群ですから、この正規部分群も巡回群になっています。
PythonSf commercial
ls=[Sb(0,1,2,3,4,5,6,7), Sb(0,1,4,5,7,6,3,2), Sb(0,1,7,6,2,3,5,4), Sb(0,2,3,1,4,6,7 ,5), Sb(0,2,4,6,5,7,1,3), Sb(0,2,5,7,3,1,6,4), Sb(0,3,1,2,4,7,5,6), Sb(0,3,4,7,6 ,5,2,1), Sb(0,3,6,5,1,2,7,4), Sb(0,4,5,1,7,3,2,6), Sb(0,4,6,2,5,1,3,7), Sb(0,4,7 ,3,6,2,1,5), Sb(0,5,1,4,7,2,6,3), Sb(0,5,3,6,1,4,2,7), Sb(0,5,7,2,3,6,4,1), Sb(0 ,6,1,7,2,4,3,5), Sb(0,6,2,4,5,3,7,1), Sb(0,6,5,3,1,7,4,2), Sb(0,7,2,5,3,4,1,6), Sb(0,7,3,4,6,1,5,2), Sb(0,7,6,1,2,5,4,3)]; kfs(x y x^-1 y^-1 for x,y in mitr(ls,ls))
===============================
kfs(Sb(0,1,2,3,4,5,6,7), Sb(0,2,4,6,5,7,1,3), Sb(0,3,6,5,1,2,7,4), Sb(0,4,5,1,7,3,2,6), Sb(0,5,7,2,3,6,4,1), Sb(0,6,1,7,2,4,3,5), Sb(0,7,3,4,6,1,5,2))
この正規部分群に対して不変な部分体、すなわち σ(x)==x となる O3 八元数要素を全て列挙します。
PythonSf commercial
kf=kfs(Sb(0,1,2,3,4,5,6,7), Sb(0,2,4,6,5,7,1,3), Sb(0,3,6,5,1,2,7,4), Sb(0,4,5,1,7,3,2,6), Sb(0,5,7,2,3,6,4,1), Sb(0,6,1,7,2,4,3,5), Sb(0,7,3,4,6,1,5,2)); [Bf.x for vc in mitr(*[3]*8) if (Bf(x=O3(vc)), all(σ(Bf.x)==Bf.x for σ in kf))[-1]]
===============================
[O3(Z3(0)), O3(0, 1, 1, 1, 1, 1, 1, 1), O3(0, 2, 2, 2, 2, 2, 2, 2), O3(Z3(1)), O3(1, 1, 1, 1, 1, 1, 1, 1), O3(1, 2, 2, 2, 2, 2, 2, 2), O3(Z3(2)), O3(2, 1, 1, 1, 1, 1, 1, 1), O3(2, 2, 2, 2, 2, 2, 2, 2)]
上の O3 の部分集合は積演算と和演算に閉じており部分体を構成します。下のように確認できます。
PythonSf commercial
ls=[O3(Z3(0)), O3(0, 1, 1, 1, 1, 1, 1, 1), O3(0, 2, 2, 2, 2, 2, 2, 2), O3(Z3(1)), O3(1, 1, 1, 1, 1, 1, 1, 1), O3(1, 2, 2, 2, 2, 2, 2, 2), O3(Z3(2)), O3(2, 1, 1, 1, 1, 1, 1, 1), O3(2, 2, 2, 2, 2, 2, 2, 2)]; all(x y in ls for x,y in mitr(ls,ls))
===============================
True
PythonSf commercial
ls=[O3(Z3(0)), O3(0, 1, 1, 1, 1, 1, 1, 1), O3(0, 2, 2, 2, 2, 2, 2, 2), O3(Z3(1)), O3(1, 1, 1, 1, 1, 1, 1, 1), O3(1, 2, 2, 2, 2, 2, 2, 2), O3(Z3(2)), O3(2, 1, 1, 1, 1, 1, 1, 1), O3(2, 2, 2, 2, 2, 2, 2, 2)]; all(x+y in ls for x,y in mitr(ls,ls))
===============================
True
位数 3 の部分群と部分体
こんどは位数 3 の部分群と部分体を構成してみます。まずは 21 個の O3 八元数の自己同型置換の中から位数が 3 の置換要素全てを列挙します
PythonSf commercial
ls=[Sb(0,1,2,3,4,5,6,7), Sb(0,1,4,5,7,6,3,2), Sb(0,1,7,6,2,3,5,4), Sb(0,2,3,1,4,6,7 ,5), Sb(0,2,4,6,5,7,1,3), Sb(0,2,5,7,3,1,6,4), Sb(0,3,1,2,4,7,5,6), Sb(0,3,4,7,6 ,5,2,1), Sb(0,3,6,5,1,2,7,4), Sb(0,4,5,1,7,3,2,6), Sb(0,4,6,2,5,1,3,7), Sb(0,4,7 ,3,6,2,1,5), Sb(0,5,1,4,7,2,6,3), Sb(0,5,3,6,1,4,2,7), Sb(0,5,7,2,3,6,4,1), Sb(0 ,6,1,7,2,4,3,5), Sb(0,6,2,4,5,3,7,1), Sb(0,6,5,3,1,7,4,2), Sb(0,7,2,5,3,4,1,6), Sb(0,7,3,4,6,1,5,2), Sb(0,7,6,1,2,5,4,3)]; [σ for σ in ls if len(kfs(σ^k for k in range(10)))==3]
===============================
[Sb(0,1,4,5,7,6,3,2), Sb(0,1,7,6,2,3,5,4), Sb(0,2,3,1,4,6,7,5), Sb(0,2,5,7,3,1,6,4), Sb(0,3,1,2,4,7,5,6), Sb(0,3,4,7,6,5,2,1), Sb(0,4,6,2,5,1,3,7), Sb(0,4,7,3,6,2,1,5), Sb(0,5,1,4,7,2,6,3), Sb(0,5,3,6,1,4,2,7), Sb(0,6,2,4,5,3,7,1), Sb(0,6,5,3,1,7,4,2), Sb(0,7,2,5,3,4,1,6), Sb(0,7,6,1,2,5,4,3)]
上の位数 3 の要素の一つが構成する 21 個の自己同型群の部分群を下のように作ります。
PythonSf commercial
σ=Sb(0,1,4,5,7,6,3,2); kfs(σ^k for k in range(10))
===============================
kfs(Sb(0,1,2,3,4,5,6,7), Sb(0,1,4,5,7,6,3,2), Sb(0,1,7,6,2,3,5,4))
上の位数 3 の群における O3 八元数部分不変体を下のように作れます。
PythonSf commercial
kf=kfs(Sb(0,1,2,3,4,5,6,7), Sb(0,1,4,5,7,6,3,2), Sb(0,1,7,6,2,3,5,4)); [Bf.x for vc in mitr(*[3]*8) if (Bf(x=O3(vc)), all(σ(Bf.x)==Bf.x for σ in kf))[-1]]
===============================
[O3(Z3(0)), O3(0, 0, 0, 1, 0, 1, 1, 0), O3(0, 0, 0, 2, 0, 2, 2, 0), O3(0, 0, 1, 0, 1, 0, 0, 1), O3(0, 0, 1, 1, 1, 1, 1, 1), O3(0, 0, 1, 2, 1, 2, 2, 1), O3(0, 0, 2, 0, 2, 0, 0, 2), O3(0, 0, 2, 1, 2, 1, 1, 2), O3(0, 0, 2, 2, 2, 2, 2, 2), O3(0, 1), O3(0, 1, 0, 1, 0, 1, 1, 0), O3(0, 1, 0, 2, 0, 2, 2, 0), O3(0, 1, 1, 0, 1, 0, 0, 1), O3(0, 1, 1, 1, 1, 1, 1, 1), O3(0, 1, 1, 2, 1, 2, 2, 1), O3(0, 1, 2, 0, 2, 0, 0, 2), O3(0, 1, 2, 1, 2, 1, 1, 2), O3(0, 1, 2, 2, 2, 2, 2, 2), O3(0, 2), O3(0, 2, 0, 1, 0, 1, 1, 0), O3(0, 2, 0, 2, 0, 2, 2, 0), O3(0, 2, 1, 0, 1, 0, 0, 1), O3(0, 2, 1, 1, 1, 1, 1, 1), O3(0, 2, 1, 2, 1, 2, 2, 1), O3(0, 2, 2, 0, 2, 0, 0, 2), O3(0, 2, 2, 1, 2, 1, 1, 2), O3(0, 2, 2, 2, 2, 2, 2, 2), O3(Z3(1)), O3(1, 0, 0, 1, 0, 1, 1, 0), O3(1, 0, 0, 2, 0, 2, 2, 0), O3(1, 0, 1, 0, 1, 0, 0, 1), O3(1, 0, 1, 1, 1, 1, 1, 1), O3(1, 0, 1, 2, 1, 2, 2, 1), O3(1, 0, 2, 0, 2, 0, 0, 2), O3(1, 0, 2, 1, 2, 1, 1, 2), O3(1, 0, 2, 2, 2, 2, 2, 2), O3(1, 1), O3(1, 1, 0, 1, 0, 1, 1, 0), O3(1, 1, 0, 2, 0, 2, 2, 0), O3(1, 1, 1, 0, 1, 0, 0, 1), O3(1, 1, 1, 1, 1, 1, 1, 1), O3(1, 1, 1, 2, 1, 2, 2, 1), O3(1, 1, 2, 0, 2, 0, 0, 2), O3(1, 1, 2, 1, 2, 1, 1, 2), O3(1, 1, 2, 2, 2, 2, 2, 2), O3(1, 2), O3(1, 2, 0, 1, 0, 1, 1, 0), O3(1, 2, 0, 2, 0, 2, 2, 0), O3(1, 2, 1, 0, 1, 0, 0, 1), O3(1, 2, 1, 1, 1, 1, 1, 1), O3(1, 2, 1, 2, 1, 2, 2, 1), O3(1, 2, 2, 0, 2, 0, 0, 2), O3(1, 2, 2, 1, 2, 1, 1, 2), O3(1, 2, 2, 2, 2, 2, 2, 2), O3(Z3(2)), O3(2, 0, 0, 1, 0, 1, 1, 0), O3(2, 0, 0, 2, 0, 2, 2, 0), O3(2, 0, 1, 0, 1, 0, 0, 1), O3(2, 0, 1, 1, 1, 1, 1, 1), O3(2, 0, 1, 2, 1, 2, 2, 1), O3(2, 0, 2, 0, 2, 0, 0, 2), O3(2, 0, 2, 1, 2, 1, 1, 2), O3(2, 0, 2, 2, 2, 2, 2, 2), O3(2, 1), O3(2, 1, 0, 1, 0, 1, 1, 0), O3(2, 1, 0, 2, 0, 2, 2, 0), O3(2, 1, 1, 0, 1, 0, 0, 1), O3(2, 1, 1, 1, 1, 1, 1, 1), O3(2, 1, 1, 2, 1, 2, 2, 1), O3(2, 1, 2, 0, 2, 0, 0, 2), O3(2, 1, 2, 1, 2, 1, 1, 2), O3(2, 1, 2, 2, 2, 2, 2, 2), O3(2, 2), O3(2, 2, 0, 1, 0, 1, 1, 0), O3(2, 2, 0, 2, 0, 2, 2, 0), O3(2, 2, 1, 0, 1, 0, 0, 1), O3(2, 2, 1, 1, 1, 1, 1, 1), O3(2, 2, 1, 2, 1, 2, 2, 1), O3(2, 2, 2, 0, 2, 0, 0, 2), O3(2, 2, 2, 1, 2, 1, 1, 2), O3(2, 2, 2, 2, 2, 2, 2, 2)]
以上により \(F\):O3(0),O3(1),O3(2):O3 八元数実数と考え、\(E\): O3 八元数全体対し \(E\) の事後同型群 \(G\):位数 21 が作られ、その部分群 H として位数 7 と 3 の二種類を作りました。この二種類の部分群に対し二種類の:すなわち位数9 と 81 の部分体 \(E^H\) を作りました。この全体を下に図時します
E^H
ls=[O3(Z3(0)), O3(0, 1, 1, 1, 1, 1, 1, 1), O3(0, 2, 2, 2, 2, 2, 2, 2), O3(Z3(1)), O3(1, 1, 1, 1, 1, 1, 1, 1), O3(1, 2, 2, 2, 2, 2, 2, 2), O3(Z3(2)), O3(2, 1, 1, 1, 1, 1, 1, 1), O3(2, 2, 2, 2, 2, 2, 2, 2)]; len(ls)
===============================
9
9^4 == 6561
kfs(Sb(0,1,2,3,4,5,6,7), Sb(0,2,4,6,5,7,1,3), Sb(0,3,6,5,1,2,7,4), Sb(0,4,5,1,7,3,2,6), Sb(0,5,7,2,3,6,4,1), Sb(0,6,1,7,2,4,3,5), Sb(0,7,3,4,6,1,5,2))
F H E
O3(0) 7
O3(1) --------------- |O3 八元数| == 3^8 == 6561
O3(2) 3 |G|==21:自己同型群
H
kf=kfs(Sb(0,1,2,3,4,5,6,7), Sb(0,1,4,5,7,6,3,2), Sb(0,1,7,6,2,3,5,4)); [Bf.x for vc in mitr(*[3]*8) if (Bf(x=O3(vc)), all(σ(Bf.x)==Bf.x for σ in kf))[-1]].__len__()
===============================
81
81^2 == 6561
kf=kfs(Sb(0,1,2,3,4,5,6,7), Sb(0,1,4,5,7,6,3,2), Sb(0,1,7,6,2,3,5,4)); [Bf.x for vc in mitr(*[3]*8) if (Bf(x=O3(vc)), all(σ(Bf.x)==Bf.x for σ in kf))[-1]]
===============================
[O3(Z3(0)), O3(0, 0, 0, 1, 0, 1, 1, 0), O3(0, 0, 0, 2, 0, 2, 2, 0), O3(0, 0, 1, 0, 1, 0, 0, 1), O3(0, 0, 1, 1, 1, 1, 1, 1), O3(0, 0, 1, 2, 1, 2, 2, 1), O3(0, 0, 2, 0, 2, 0, 0, 2), O3(0, 0, 2, 1, 2, 1, 1, 2), O3(0, 0, 2, 2, 2, 2, 2, 2), O3(0, 1), O3(0, 1, 0, 1, 0, 1, 1, 0), O3(0, 1, 0, 2, 0, 2, 2, 0), O3(0, 1, 1, 0, 1, 0, 0, 1), O3(0, 1, 1, 1, 1, 1, 1, 1), O3(0, 1, 1, 2, 1, 2, 2, 1), O3(0, 1, 2, 0, 2, 0, 0, 2), O3(0, 1, 2, 1, 2, 1, 1, 2), O3(0, 1, 2, 2, 2, 2, 2, 2), O3(0, 2), O3(0, 2, 0, 1, 0, 1, 1, 0), O3(0, 2, 0, 2, 0, 2, 2, 0), O3(0, 2, 1, 0, 1, 0, 0, 1), O3(0, 2, 1, 1, 1, 1, 1, 1), O3(0, 2, 1, 2, 1, 2, 2, 1), O3(0, 2, 2, 0, 2, 0, 0, 2), O3(0, 2, 2, 1, 2, 1, 1, 2), O3(0, 2, 2, 2, 2, 2, 2, 2), O3(Z3(1)), O3(1, 0, 0, 1, 0, 1, 1, 0), O3(1, 0, 0, 2, 0, 2, 2, 0), O3(1, 0, 1, 0, 1, 0, 0, 1), O3(1, 0, 1, 1, 1, 1, 1, 1), O3(1, 0, 1, 2, 1, 2, 2, 1), O3(1, 0, 2, 0, 2, 0, 0, 2), O3(1, 0, 2, 1, 2, 1, 1, 2), O3(1, 0, 2, 2, 2, 2, 2, 2), O3(1, 1), O3(1, 1, 0, 1, 0, 1, 1, 0), O3(1, 1, 0, 2, 0, 2, 2, 0), O3(1, 1, 1, 0, 1, 0, 0, 1), O3(1, 1, 1, 1, 1, 1, 1, 1), O3(1, 1, 1, 2, 1, 2, 2, 1), O3(1, 1, 2, 0, 2, 0, 0, 2), O3(1, 1, 2, 1, 2, 1, 1, 2), O3(1, 1, 2, 2, 2, 2, 2, 2), O3(1, 2), O3(1, 2, 0, 1, 0, 1, 1, 0), O3(1, 2, 0, 2, 0, 2, 2, 0), O3(1, 2, 1, 0, 1, 0, 0, 1), O3(1, 2, 1, 1, 1, 1, 1, 1), O3(1, 2, 1, 2, 1, 2, 2, 1), O3(1, 2, 2, 0, 2, 0, 0, 2), O3(1, 2, 2, 1, 2, 1, 1, 2), O3(1, 2, 2, 2, 2, 2, 2, 2), O3(Z3(2)), O3(2, 0, 0, 1, 0, 1, 1, 0), O3(2, 0, 0, 2, 0, 2, 2, 0), O3(2, 0, 1, 0, 1, 0, 0, 1), O3(2, 0, 1, 1, 1, 1, 1, 1), O3(2, 0, 1, 2, 1, 2, 2, 1), O3(2, 0, 2, 0, 2, 0, 0, 2), O3(2, 0, 2, 1, 2, 1, 1, 2), O3(2, 0, 2, 2, 2, 2, 2, 2), O3(2, 1), O3(2, 1, 0, 1, 0, 1, 1, 0), O3(2, 1, 0, 2, 0, 2, 2, 0), O3(2, 1, 1, 0, 1, 0, 0, 1), O3(2, 1, 1, 1, 1, 1, 1, 1), O3(2, 1, 1, 2, 1, 2, 2, 1), O3(2, 1, 2, 0, 2, 0, 0, 2), O3(2, 1, 2, 1, 2, 1, 1, 2), O3(2, 1, 2, 2, 2, 2, 2, 2), O3(2, 2), O3(2, 2, 0, 1, 0, 1, 1, 0), O3(2, 2, 0, 2, 0, 2, 2, 0), O3(2, 2, 1, 0, 1, 0, 0, 1), O3(2, 2, 1, 1, 1, 1, 1, 1), O3(2, 2, 1, 2, 1, 2, 2, 1), O3(2, 2, 2, 0, 2, 0, 0, 2), O3(2, 2, 2, 1, 2, 1, 1, 2), O3(2, 2, 2, 2, 2, 2, 2, 2)]
E^H
blog comments powered by Disqus