secrets of ε0,μ0: considerations of SI system of units from a natural unit system--Eng unit_systems
introduction
Can you accept the definitions of a unit current and μ0 in the SI system of units
The ampere is that constant current which, if maintained in two straight parallel conductors of infinite length, of negligible circular crosssection, and placed 1 meter apart in vacuum, would produce between these conductors a force equal to 2 × 10^-7 newton per meter of length. It follows that the magnetic constant μ0, also known as the permeability of vacuum, is exactly 4π × 10^-7 henries per meter, μ0 = 4π × 10^-7 H/m.
The sentence after “It follows” is absurd. What is the permeability of vacuum, There is a big jump in the logic. (Moreover there is no other explanation for the permeability of vacuum in the standards). The drived unit of μ0 should be Newton/A^2. It is a circular reasoning to use the H:henry that must be drived from the A:Ampere basic unit. Because the H:henry drived unit contains A:ampere unit.
Let’s go back to more basics. At Gausian unit system ε0,μ0 are 1 and are physical quantities without units. It is not logical that the physical quantities without unit become quantities with units associated with a selection of basic units.
(I claim that the definition of the unit of current should be modified to one that was described afterwards)
I show followings in this consiterations.
- The upper critiques or queries are right.
- ε0・μ0 are 1 without units in nature. But if you chose the MKSA system of units, then ε0,μ0 become not 1 physical quantities with units.
- ε0・μ0 は本質的に無次元の 1 である。それにも関わらず「単位電流もしくは単位電荷を基本単位として採用すると、SI 単位系のような物理量の次元を持った ε0・μ0 を持つ四元単位系になってしまう。
- これらの疑問・批判を解消する明晰な単位電流の定義の仕方を提示します。
Also I show followigs.
- ε0 and μ0 in SI system of units are brought about by historical sequence of events. Physics doesn’t need ε0 and μ0.
- The unnecesary physical constants:ε0 and μ0 have brought about “electric field and dielectric flux” or “magnetic field and magnetic flux” of different value and different derived units even in vacuum. Though they should be same values and same derived units.
- If you chose Heaviside-Lorentz system of units, then these physical quantities become same value and same derived units.
However, SI system of units is too complex by historical sequence of events to advance considerations. So I mainly use the natural units that is simple and of good prospect. Happily I have embedded the natural units and Planck units and others in PythonSf module sfCrrntIniRelativity.py and sfCrrntIniOpRelativity.py that was distributed as an example to customize PythonSf. Using this file, you can calculate expressions which appear on the considerations of systems of units. ただし、この論考を進めるには、SI 単位系は歴史的経緯のために複雑になりすぎています。より単純で見通しの良い自然単位系を主に使います。幸いにも PythonSf では「ユーザー・カスタマイズ例として配布している Python モジュール・ファイル sfCrrntIniRelativity.py sfCrrntIniOpRelativity.py」に、自然単位系やプランク単位系を実装しています。これを使うことで、単位系の考察に出てくる数式を実際に計算可能なものにできます。論考を数値実験で確認していけます。実際に計算することで、論考に矛盾が入り込んで来ていないことを数値実験で確認していけます。 論考を実際に動くプログラム動作で確認できることは、論考全体が正しいことを強く示唆してくれます。 一箇所でも論考に矛盾が入り込んだら、プログラム動作に矛盾が生じてくるからです。
そもそも循環論法に陥ることなく電磁系の世界の組み立て単位全てを基本から構築するには、電磁系の世界は複雑すぎます。コンピュータの助けを借りて初めて理解可能な複雑さになっています。コンピュータに実装された計算可能な単位系に誤解・誤りが入り込んでいたら何処かに矛盾が生じます。矛盾を発生させないコンピュータ計算可能な組み立て単位系のプログラムを実装できたら、その人は電磁系の世界の組み立て単位系を正しく理解できたと言えるでしょう。(循環論法が入り込んだら、未定義変数エラーとなってプログラムは動きません)
以下の考察により、MKS:長さ・質量・時間の三つで記述される機械系の世界に、電磁気の物理世界が斜めに捻くれて組み合わされていることを示します。これが「根本的に見逃されていた何か」です。この論考の副産物として、解説されることの少ない微細構造定数の物理的意味が明確になります。
以下の論考では PythonSf を使うので、実際に数値実験も可能な PythonSf ワン・ライナー式を多用します。読者が この論考の一部に飛躍や疑問を感じたら、自分で数値実験を行うことで、論理飛躍を埋め、疑問を解消できます。以下の文章は、PythonSf のワン・ライナーが「論文や教科書を読んでいくとき・論考を積み重ねていくときの強力なツールになる」ことの実例にもなっています。是非とも以下の論考を鵜呑みにするのではなく、御自分でも批判的に読んでいくと同時に、御自分の手と頭とコンピュータを活用して数値実験をしながら読んでいってください。PythonSf ワン・ライナー式は殆ど数式と同じですから、Python や PythonSf 式の詳細を知らなくても、数学・電磁気学を知っていれば、御自分で試したい数式に簡単に変形して実行できます。ワン・ライナー式の変形だけですから、プログラミングしている感じは全く感じないでしょう。
Windows 版だけですが こちらにポータブル版の PythonSfを置いてあります。これを使えばインストール作業さえ無しで、PythonSf one-liners 数式を扱えます・計算・数値実験できます。批判も歓迎しますが、妄想や歪曲での批判ではなく、PythonSf 式でも記述される数値実験可能な批判にしてください。矛盾点があれば、コンピュータ計算が可能な PythonSf 式として矛盾点を記述できるはずです。
以下の論考は学部レベルの電磁気学と それに必要な数学を理解していることを前提とします。同時に自分の頭で考えられる、すなわち自分で自分に問題定義して、同時に その問題を解決しながら論考を進められる能力を必要とします。循環論法に陥ったことを自分で気付ける感性が必要です。逆に自分の頭で考えられるならば、使われる数式は単純な乗除べき乗算が大部分であり、高校生でも論理展開を追っていけます。自分で式を変形して数値実験可能です。高校生にとっては論理飛躍が多く、手間はかかるでしょうが、PythonSf one-liners を活用すれば、その論理飛躍も自分で埋められるでしょう。物理的意味も読み取れるでしょう。
PythonSf と自然単位系
PythonSf では sfCrrntIniRelativity.py/sfCrrntIniOpRelativity.py の名前のファイルも配布しています。カレント・ディレクトリにあります。このファイル名を sfCrrntIni.py/sfCrrntIniOp.py に変更してやると、PythonSf で自然単位系を扱えるようになります。(既存の sfCrrnitIni.py sfCrrntIniOp.py は別のファイル名に変更してください。または単位系専用のディレクトリを用意してください。)
自然単位系は光速度:c` とプランク定数:h``:\(\hbar\)(1/2pi で割られたほう) と 1 electronVolt を 1 となるように基本単位を選択した単位系です。相対論や量子力学での計算が楽になります。
PythonSf では変数名の最初と最後に backquote:` 文字を追加した変数名を使用できるように名前空間を拡張しています。例えば物理で多用される光速度 c の一文字に光速度の意味を与えることは、Python 変数と衝突するので無理です。ですから c` の二文字に光速度の意味を与えています。Naming convention として物理単位・定数には変数名の最後に ` を付加します。多用される数学記号には変数名の最初に ` を付けます。例えば `i には単位純虚数を、`X には加減乗除べき乗算が可能な恒等関数を割り当てています。
数値実験を行うとき、コンピュータ計算での浮動小数点誤差が付きまといます。光速度のような大きな数やプランク定数のような小さな数を入れたまま浮動小数点計算をすると、浮動小数点がもたらす計算誤差を含んだ正しいらしい値なのか、それとも元の数式が誤っていたのかの判別が困難になります。相対論や量子論での数値実験・浮動小数点計算を行うためには、自然単位系が必須となります。
数値計算のためだけでなく、電磁単位系を考察していく際にも自然単位系が合理的です。SI 単位系では天下りに与えられる・または辻褄あわせでしか導けなった ε0,μ0 の物理次元が、Coulomb の法則・電磁誘導の法則から物理的必然として明晰に導かれます。SI:MKSA 単位系では物理的意味の不明な電圧組み立て単位:kg m^2/(A s^3), 抵抗組み立て単位:kg m^2/(A^2 s^3) を、辻褄あわせではなく、物理的な意味を伴った必然の物理量として組み立て・導出できます。
sfCrrntIniRelativity.py/sfCrrntIniOpRelativity.py ファイルの中で自然単位系での四つの基本単位・組み立て単位を接尾辞に n を付加することで下のように定義しています。
- 基本単位 単位長:mn`, 単位質量:gn`, 単位時間:sn`, 単位電荷:Cn`
- 組立単位 単位力:Nn`, 単位仕事:Jn`, 単位電圧:Vn`, 電磁系単位電圧:dVn`, ε0:e0n`, μ0:u0n`, プランク定数(2pi で割った量):hn``, 光速度:cn`
- 素電荷 pQn`
素電荷を除き これらの値は数値の 1 にすぎません。そうなるように基本単位量を選択したのですから。
1==mn`==gn`==sn`==Cn`==eVn`==Nn`==Jn`==Vn`==dVn`==e0n`=u0n`==hn``==cn`
===============================
True
tt() 関数を呼び出すことで、これらの値が単位付きの値に変わります。値が 1 であることは変わりません。ただし単位が異なるときは等式が成立しなくなります。下のような具合です。
tt(); mn`, gn`, mn`==gn`
===============================
(mn`, gn`, False)
単位速度 == 光速度を下の PythonSf 式で確認できます
tt(); mn`/sn`, mn`/sn`==cn`
===============================
(mn`/sn`, True)
自然単位系の物理量を引数値として toSI(..) 関数で呼び出すと SI 単位系での物理量にが返ってきます。下のような具合です
自然単位系での単位長さの 3 倍を SI 単位系での長さにする
tt(); toSI(3mn`)
===============================
5.91976192003756e-7*m`
tt() 関数を呼び出さないと、mn` gn` sn` Cn` eVn` Nn` Jn` Vn` dVn` e0n` u0n` hn`` cn` は単位を伴わない単なる数値 1 の変数ラベルになっています。その様な変数ラベルであったとしても、物理的に意味を持った PythonSf 式を書くときに、変数ラベルを追加するだけで物理的意味を明示するという意味で有用です。Python 関数の多くは sympy 単位属性をもった変数を引数に与えるとエラーになることが多いので、そのときは上の単位系を伴わないラベルを使わねばなりません。一方で PythonSf 基本関数および その組み合わせだけならば、sympy 単位属性を持っていても許されます。ただし sqrt(..) 以外の PythonSf 基本関数に与える単位付きの変数は無次元の物理量に戻る式値でないとエラーになります。
# 光速度の 0.8 倍の速度と光速度の比の sin(.) 値を計算する。
v=0.8 mn`/sn`; np.sin(v/cn`)
===============================
0.7173560909
# np は numpy module であり、PythonSf 式では import 済みのグローバル変数です。
tt(); v=0.8 mn`/sn`; np
===============================
<module 'numpy' from 'C:\Python27\lib\site-packages\numpy\__init__.pyc'>
# PythonSf が備える基本関数は sympy 単位付での無次元変数を受け付けます。
tt(); v=0.8 mn`/sn`; sin(v/cn`)
===============================
0.7173560909
# 単位長さ mn` は、tt() 呼び出しの前は整数の 1 ですが、呼び出し後は単位付きの 1 即ち mn` です。
print mn`; tt(); print mn`;
1
mn`
# 0.8 mn`/sn` を光速度で割った値は、物理的には無次元の 1 ですが sympy 単位値であり numpy.sin ではエラーになります。
tt(); v=0.8 mn`/sn`; np.sin(v/cn`)
Traceback (most recent call last):
File "C:\Python27\lib\runpy.py", line 162, in _run_module_as_main
"__main__", fname, loader, pkg_name)
.
snipped
AttributeError: 'Float' object has no attribute 'sin'
以下、この PythonSf 自然単位系の計算機能を使って数値実験しながら、また物理的意味を明確にしながら、ε0, 電圧:kg m^2/(A s^3), 抵抗:kg m^2/(A^2 s^3), μ0 の組み立て単位を純を追って導出していきます。SI:MKSA 単位系では、これらは天下りに与えられ、また辻褄合わせで出てくるだけでした。
以下の考察は実際に PythonSf で計算可能な式を使って行っていきます。皆様もぜひ自分でも計算しながら読んでみてください。自分で自分自身に問題提義しながら、ここでは書いていないことも含めて、御自分の頭でも考えながら読み進めてください。誤りがあったら、コンピュータの計算結果が想定外の値を返すので容易に気付けます。
クーロン力と 単位電荷・単位力と ε0
ここではクーロン力と単位電荷から ε0 を論理的に導出・組み立てます。それが二種類の同じ力という物理量の換算率であり、本質的に無次元の 1 の量 であることを示します。
さて力は Newton 力学で 質量 * 加速度 定義されていますから、力の組み立て単位は下のようになります。
自然単位系での単位力≡質量 x 加速度
tt(); gn` mn`/sn`^2
===============================
gn`*mn`/sn`**2
でも同時にクーロンの法則を使っても力を定義できます。単位距離だけ離れた単位電荷の間には 単位力/(4pi) の力が働きます。ですから下の式・組み立て単位も力を示します。(注意: Cn^2/mn^2 が力の組立単位であるとは教科書には書いてありません。もし そのような教科書があったら教えてください)
クーロンの法則による単位力
tt(); Cn`^2/mn`^2
===============================
Cn`**2/mn`**2
ちょっと待ってください。同じ力でありながら、gn*mn/sn**2 と Cn**2/mn**2 の二つの組み立て単位が出てきました。これはどういうことでしょうか。
これは基本単位系に冗長性があるためです。単位長さ:m と単位質量:g と単位時間:sの他に単位電荷:C の四つの基本単位からなる四元単位系:mgsCを採用したことで、単位系に冗長性が発生したのです。そのため力を現すのに g m s^-2 の組み立て単位の他に、クーロンの法則から導かれる C/m^2 も力の組み立て単位になってしまったわけです。(冗長さを伴わない mgs の三元系のまま電磁気量を組み立てていくことも可能です。ただし、そのような単位系では組み立て単位に 1/2 べき乗の量が入り込んでしまいます。そのような Heaviside-Lorentz 単位系も後で考察・検討します。)
ここで下のように「電磁系の力の組立単位:C/m^2」から「機械系の力の組み立て単位:g m s^-2」への力同士の単位換算定数 e0 を導入してやれば二つの力を互いに変換できます。
# 自然単位系での電気定数:ε0 および 単位 Coulomb 力と単位力の比
tt(); e0n`, (Cn`/mn`^2)/(gn` mn`/sn`^2)
===============================
(Cn`**2*sn`**2/(gn`*mn`**3), Cn`*sn`**2/(gn`*mn`**3))
# 単位 Coulomb 力に電気定数:ε0 を掛けて単位力に変換する
tt(); (Cn`^2/mn`^2) e0n`
===============================
gn`*mn`/sn`**2
そして実際に SI:MKSA 単位系での電気定数:ε0 の組み立て単位も、上と同様に実際に Coulomb 力と機械系の力:F=m α の比になっています。下のような具合です。
# SI 単位系の電気定数:真空の誘電率:e0` は力と力の比:rate
ts(); e0`/jsw`
===============================
8.854187816e-12*A`**2*s`**4/(kg`*m`**3)
# 上の e0` の組立単位は下のように 電磁系の世界のForce/機械系の世界のForce の比の式に変形できます。
A`**2*s`**4/(kg`*m`**3) == A`**2*s`^2/m^2 s^2/(kg`*m`) == C^2/m^2 1/(kg m`/s^2)
Python sf での MKSAV 五元単位系と jsw 変換定数
Python sf では MKSA 四元単位系ではなく、後で説明するような理由で、さらに電圧 V も基本単位した MKSAV 五元単位系で実装してあります。ですから電気定数 ε0 は下のような組み立て単位で定義してあります。ts(); e0` =============================== 8.854187816e-12*A`*s`/(V`*m`)ただし、A`*s`/V`*m` では SI 単位系で定義してある組み立て単位ではないので jsw` で割ってやることで SI 単位系での組み立て単位に変更します。ここで jsw` はジュール/秒/ワット:J`/s`/W` で定義される本質的に無次元の 1 の組み立て単位です。ts(); jsw`, J`/s`/W` =============================== (kg`*m`**2/(A`*V`*s`**3), kg`*m`**2/(A`*V`*s`**3))MSAV 四元単位系では A`**2*s`**4/(kg`*m`**3) と物理的には同じだけど組み立て方が異なる A`*s`/(V`*m`) 表記になるため、 jsw` を掛けたり割ったりすることで、MKSA 組み立て単位に、ユーザーが自分で明示的に変換します。
真空の誘電「率」
SI 単位系では e0 のことを 真空の誘電「率」 と呼びます。率という漢字は無次元の量に使います。単位を持った物理量ならば 真空の誘電「度」 と言うべきです。でも以上の議論で示されるように ε0 は、同じ単位力の物理量 C/m^2 と g m s^-2 の換算定数にすぎません。本質的に無次元の 1 の量です。ε0 を 真空の誘電「率」 と電磁気学の教科書で書いてあることは正しいのです。
ちなみに 1 であった自然単位系での力の単位の換算定数:真空の誘電率は toSI(..) 関数によって下のように SI 単位系での真空の誘電率に変換されます。
tt(); toSI(e0n`), toSI(e0n`) jsw`, e0`
===============================
(8.854187816e-12*A`**2*s`**4/(kg`*m`**3), 8.854187816e-12*A`*s`/(m`*V`), 8.854187816e-12*A`*s`/(m`*V`))
同じ 物理量:力どうしの変換係数ですから自然単位系で 1 の量である e0n が SI 単位系での真空の誘電率:電気定数: e0 に正しく変換されます。このことからも SI 単位系での電気定数も本質的に無次元の 1 であることが解ります。(私自身は上の e0n の導出のしかたと、この e0n と e0 が同じ物理量であるがゆえに toSI(..) 関数で変換できることを知って、やっと電気定数:e0 の物理的意味を理解できた気になれました。皆様は如何でしょうか?)
冗長性のない長さ・質量・時間だけの MKS 三元単位系ならば、このような冗長性は発生しません。ε0,μ0 の変数は発生しません。実際に三元単位系である cgs 単位系や Heaviside-Lorentz 単位系では ε0,μ0 のような物理定数は出てきません。
例えて言えば、ε0 は inch と cm の間の長さの換算定数みたいなものです。下の式にある換算定数 EK の単位は inch/cm だといっても、長さの換算「率」です。「度」とはなりません。
# inch = EK cm
ts(); EK = inch`/cm`; EK
===============================
2.54000000000000
ただし、inch と cm の二つを共存させる必要はないので、こんな単位の換算「率」を通常は考えません。しかし電磁系の世界は質量・長さ・時間だけで完結する機械系の世界とは独立して並在します。共存させねばなりません。現実の物理世界は電磁系と機械系の二つが並存しているので、電磁系と機械系の二種類の単位系が並立します。しかも、この二つの世界を機械系の MKS だけで記述しようとすると電磁系の世界には 1/2 乗の組み立て単位が入り込んできます。私には、何か捻られて・斜めに交わった二つの世界が並立しているように見えます。皆様は如何でしょうか?
電磁系・機械系二つの世界が斜めに交わって共存している
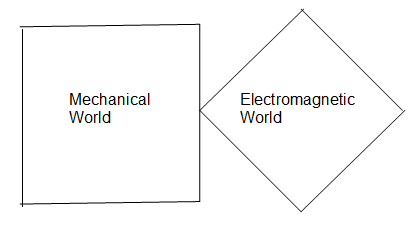
電圧の単位:kg m^2/(A s^3) の導出
単位電圧とは、単位電荷を単位エネルギーだけ持ち上げるポテンシャルのことです。ですから 単位電圧:V * 単位電荷:C == 単位エネルギーとなります。この関係より下のように単位電圧の組立単位を導出できます。
単位電圧:V;; gn` mn`^2/sn`^2 /Cn`
===============================
gn`*mn`**2/(Cn`*sn`**2)
tt(); Vn`
===============================
gn`*mn`**2/(Cn`*sn`**2)
これにより SI 単位系での訳の解らない下の電圧単位:kg m^2/(A s^3) が導けました。C を A s で置き換えれば下の電圧単位になります。
import sympy.physics.units as un; un.V
===============================
kg*m**2/(A*s**3)
「V I == W の関係式から電圧の組み立て単位 kg m^2/(A s^3) を導出した」とし、SI 単位系での電圧の組み立て単位になんらの疑問を持たない方が多くいます。大多数の電気・回路技術者に「100 kg m^2/(A s^3) の電圧」と言っても通じないのにも関わらず平気でいられる方たちです。でも私は SI 単位系での電圧の組み立て単位:kg m^2/(A s^3) を理解できない方のほうが正しいと主張します。電圧の組み立て単位を導出しようとしているのに、 V I == W の関係式を持ち出すのは循環論法です。V I == W の関係式は電圧組み立て単位を導出した後に、下のような順序で導出される関係式です。「V I == W の関係式から電圧の組み立て単位 kg m^2/(A s^3) を導いた」のは、導出ではなく単なる辻褄合わせ:fitting だと私は主張します。単なる fitting で導いた「kg m^2/(A s^3) の電圧組立単位」が電気・回路技術者に通じないのは当然だと主張します。
# V I == W の導出
V q == Energy →両辺を時間で微分する→ V dq/dt = V I = dE/dt = W
大多数の電気・回路技術者は、そして物理学者の多くも、ここで述べたような基本回路からの電圧の組み立てを行っていません。辻褄合わせにすぎません。ですから、100 kg m^2/(A s^3) の電圧と言われても 100V の意味だと理解できません。
そんな彼らに「100 kg m/s^2/m^2 の圧力」「100 N/m^2 の圧力」「100 Pa の圧力」いずれの組み立て単位で圧力を表現しても通じるでしょう。もし「100 N/m^2 の圧力」で通じなかったら、彼らは圧力という物理概念を理解していないことを意味します。でも「100 kg m^2/(A s^3) の電圧」が通じない技術者・物理学者が電圧の概念を理解していないわけではありません。彼らは電圧を組立単位ではなく、質量ではなく電圧を基本単位に使う MSAV 四元単位系で閉じた電磁系の世界で検討・設計しているからです。この詳細はPythonSf MKS + A V 単位系の章で論考します。
二つの電圧の組み立て単位
mgsC 四元単位系では、力の単位が g m/s^2 と C^2/m^2 の二種類が許されたように、電圧の組立単位も g m^2/(C s^2) の他に、もうひとつの別の組立単位が許されます。
C^2/m^2 が力ならば C^2/m はエネルギーです。ポテンシャル電圧は単位電荷あたりのエネルギーですから、C/m も単位電圧とみなせます。
力 ;; Cn`^2/mn`^2
エネルギー;; Cn`^2/mn`
# ポテンシャル電圧 ≡ 単位電荷あたりのエネルギー
電圧;; Cn`/mn`
ε0 は無次元の単位換算定数でした。ε0 を先の組み立て単位電圧:g m^2/(C s^2) に掛けてやれば、実際に今回の組み立て単位電圧の C/m になります。
tt(); e0n` gn` mn`^2/sn`^2 /Cn`
===============================
Cn`/mn`
電圧組み立て単位:g m^2/(C s^2) は機械系と電磁系の両方にまたがる電圧単位と解釈できます。もう一方の電圧組み立て単位:C/m は、電磁系内で閉じた電圧単位とみなせます。この意味での電圧名称として dV を sfCrrntIniRelativity.py/sfCrrntIniOpRelativity.py に定義してあります。
tt(); dVn`
===============================
Cn`/mn`
tt(); toSI(dVn`)
===============================
2.68126520285301e-12*A`*s`/m`
注意! Cn/mn を電圧としても良いとする電磁気学の教科書はないと思います。でも MKSA 単位系は冗長な単位系であり、力のときと同様に Cn/mn を電圧ともできると私は主張します。
また この電圧:Cn/mn が √(力) と同じであることを確認しておくと、後でHeaviside-Lorentz 単位系を四元単位系として扱い 1/2 乗を出てこなくするとき役立ちます。
ここで行った SI 単位系の抵抗組立単位 kg m^2/(A^2 s^3) の導出は、物理法則に従って単位力の二重性から電圧を組み立て、その次に抵抗≡電圧/電流の定義から抵抗の組み立て単位を組み立てたものです。Ω=V/A=W/A^2=J/(A^2 s)=Nm/(A^2 s)=kg m^2/(A^2 s^3) の順序で SI 単位系での抵抗の組み立て単位を導出することもできますが、これは単なる辻褄合わせです。循環論法です。上でのように先に電圧を定義してあったからこそ Ω == V/A == W/A^2 の関係式が導かれるのです。
電場と分極
VとC/m が同じなら V/m と C/m^2 すなわち 電場:E と 分極:P も同じです。ε0 E と P は同じ組み立て単位になります。「E は同じ物理量の機械系・電磁系にまたがる表現」と、「P は電磁系だけに閉じた表現」とみなすことも可能です。
このように考えると「Maxwell 方程式に出てくる分極電流の意味が より納得できる」・「Maxwell が分極電流に至れたことも理解できる」と思います。逆に言えば「電場:E と 分極:P が同じ物理量である」との認識が元にないと、分極電流なんて思いつけないでしょう。如何でしょうか?
抵抗の組み立て単位:kg m^2/(A^2 s^3) の導出
電圧の単位:g m^2/(C s^2) または kg m^2/(A s^3) を導出できれば、単位抵抗≡「単位電圧を与えたとき単位電流を流す抵抗」:Ω= V/I より、SI:MKSA 単位系の、下の訳の分からない抵抗単位を導出できます。
import sympy.physics.units as un; un.ohm
===============================
kg*m**2/(A**2*s**3)
下の Cn を A s で置き換えれば、上の式になります。自然単位系での抵抗の組み立て単位が SI 単位系での抵抗の組み立て単位になります。
抵抗 Ω≡V/I;; tt(); V,I=gn` mn`^2/sn`^2 /Cn`, Cn`/sn`; V/I
===============================
gn`*mn`**2/(Cn`**2*sn`)
ちなみに上の自然単位系での単位抵抗 V/I を SI:MKSA 単位系での値に換算してやると下のようになります。
抵抗 Ω;; tt(); I,V=Cn`/sn`, gn` mn`^2/sn`^2 /Cn`; toSI(V/I), toSI(V/I) W` s`/J`
===============================
(376.730313530715*kg`*m`**2/(A`**2*s`**3), 376.730313530715*V`/A`)
自然単位系の単位抵抗は SI 単位系では 377Ω 弱の抵抗値です。1electron Volt が 1 になるように定めた単位系であること、単位電荷が素電荷に近いことから、1Ω と三桁しか違わない 377Ω の値も納得できます。「元々電磁現象は原子レベルでの物理現象が日常の MKS のレベルにまで顕現してきた現象である」・「だから 17世紀まで電磁現象が人類には認識されなかった」ことが理解できます。如何でしょうか。
ここで行った SI 単位系の抵抗組立単位 kg m^2/(A^2 s^3) の導出は、物理法則に従って単位力の二重性から電圧を組み立て、その次に抵抗≡電圧/電流の定義から抵抗の組み立て単位を組み立てたものです。単位電流の定義から抵抗の組み立て単位を物理法則に従って構築するのは、この倍以上面倒です。大多数の電気・回路設計者は、こんな面倒な抵抗単位の組み立てなど考えたこともありません。Ω=V/A=W/A^2=J/(A^2 s)=Nm/(A^2 s)=kg m^2/(A^2 s^3) の順序で SI 単位系での抵抗の組み立て単位を導出することもできますが、これは単なる辻褄合わせです。循環論法です。そんな彼らに「100 kg m^2/(A^2 s^3) の抵抗」と言っても通じないのは当然です。彼らは「MSAV の四元単位系で記述される閉じた電磁系の世界」で設計・考察しているのですから。このことについてはPythonSf MKS+A V 単位系 の節で論考します。
μ0n 組み立て単位の導出
単位長さ当たり 10ターンだけ巻いたコイルに 0.1C/s の電流を流せば 1 単位電流・ターンの単位磁場がコイルの中に生成されます。
単位磁場
nTurn, I=10, 0.1Cn`/sn`; nTurn I/mn`
===============================
1.0*Cn`/(mn`*sn`)
単位時間に単位磁場分だけ変化すれば、単位面積のループには単位電圧が発生します
tt(); nTurn, I=10, 0.1Cn`/sn`; Velectric=nTurn I/mn` 1/sn` mn`^2; Velectric
===============================
1.0*Cn`*mn`/sn`**2
この電圧単位は、質量 gn を含みません。電磁系の世界で閉じた範囲での組立単位です。先に導いた電圧:V=gn*mn**2/(Cn*sn**2) は単位質量 gn と単位電荷 C を含んだ機械系の世界と電磁系の世界の両方にまたがった組み立て単位です。でも これは単位系の冗長性の結果であり、両者:V と Velectric は同じ電圧という物理量を表しています。本質的に同じ物理量の比率:V/Velectric が、u0n になります。四元単位系の冗長性の結果として u0n は下の物理次元となります。
tt(); V=gn`*mn`**2/(Cn`*sn`**2); nTurn, I=10, 0.1Cn`/sn`; Velectric=nTurn I/mn` 1/sn` mn`^2; V/Velectric, u0n`
===============================
(1.0*gn`*mn`/Cn`**2, gn`*mn`/Cn`**2)
ちなみに この u0n と、SI 単位系の u0 は下のように本質的に同じ物理量です。
tt(); toSI(u0n`), u0`, u0` jsw`
===============================
(1.25663706166589e-6*kg`*m`/(A`**2*s`**2), 1.2566370614e-6*s`*V`/(A`*m`), 1.2566370614e-6*kg`*m`/(A`**2*s`**2))
e0n が機械系での力と電磁系での力の比であり、本質的に無次元の物量でした。同様に「u0n も V/Velectric であり、本質的に無次元の物理量です」としたいのですが、残念ながらそのようには実装していません。その理由を次の節で説明します。
e0n,u0n と光速度 C
上の e0n,u0n の導出では光速度が入っいません。でも下のように e0n と u0n の積は (sn/mn)^2==1/c^2 になります。自動的に光速度が出てきてしまいます。μ0n ≡ V/Velectric と本質的に無次元の量のはずなのに、e0n も無次元の量だったのに e0n と u0n の積が 1/光速度の自乗の次元になるのは変です。
tt(); e0n` u0n`
===============================
sn`**2/mn`**2
e0n u0n == 1/光速度^2 となる理由は、「単位時間あたりに単位磁場分だけ変化すれば、単位面積のループには単位電圧:Velectric が発生します」として V と Velectric の比率を u0n としたことにあります。μ0n の単位を無次元にするためには相対論的な時空幾何学で統一して考えるべきであり、単位時間あたりに ではなく 単位長さあたり ≡ 光速度x単位時間あたり とすべきでした。電流も 単位時間あたりの電荷 ではなく 光速度x単位時間あたりの電荷 とすべきでした。 光速度x を省略してしまったことにより μ0n に 1/光速度^2 が入り込みました。μ0n に 1/光速度^2 が入り込んだのは esu 単位系の流儀で組み立て単位系を導出してきたためだとも言えます 。emu 単位系の流儀で組立単位を構築していってやれば、u0n は無次元の 1 になりますが、e0n が 1/光速度^2 になります。
物理理論の綺麗さのためには、1/c^2 を外側に出してμ0n も無次元の定数とすべきです。でも既に SI 単位系が浸透しすぎています。toSI(u0n`) == u0` とするために、μ0n を無次元にするのではなく 1/光速度^2 とする実装を選択しました。でも ε0,μ0 が本質的には無次元の 1 であり、四元単位系の冗長性故に物理次元を持つのだと主張します。光速度 c は相対論的な時空幾何学の視点では無次元の 1 となるべき物理量だからです。
PythonSf の自然単位系プログラムの実装では u0n の定義を実際には u0n=cn^2/e0n で行っています。でも その背景には このような物理的な理由があります。辻褄合わせではありません。
h`` と c` と単位電荷と微細構造定数
実は sfCrrntIniRelativity.py/sfCrrntIniOpRelativity には Planck 単位系と自然単位系のほかに、素電荷を 1 とするけれど ε0,μ0 を 1 としない修正自然単位系のコードも実装してあります。(さらには Stoney単位系も実装してあるのですが、今回は使いません。) 「素電荷を単位電荷とする単位系を考えやすくするため」また「素電荷と単位電荷の関係を明確にするため」、この Planck 単位系と修正自然単位系を使います。
なお以下の考察の副産物として「解説されることの少ない微細構造定数の物理的意味」・「Pauli が微細構造定数を追求し続けた理由」も解るでしょう。
Planck 単位系
Planck 単位系は光速度:c と Planck 定数:h``:\(\hbar\) と万有引力定数を 1 となるように基本単位を選択した単位系です。一般相対論や重力を含む量子力学での計算が楽になります。
sfCrrntIniRelativity.py/sfCrrntIniOpRelativity.py ファイルの中で Planck 単位系の単位を下のように接尾辞に p を付けた変数として定義しています。
- 基本単位 単位長:mp`, 単位質量:gp`, 単位時間:sp`, 単位電荷:Cp`
- 組立単位 単位力:Np`, 単位仕事:Jp`, 単位電圧:Vp`, 単位磁束密度:Tp`, 電磁系単位電圧:dVp`, ε0:e0p`, μ0:u0n`, プランク定数(2pi で割った量):hp``, 光速度:cp`
- 素電荷 eQp`
素電荷を除き これらの値は 1 にすぎません。そうなるように基本単位量を選択したのですから。
驚くべきことなのですが、この Planck 単位系での単位電荷と自然単位系での単位電荷は、全く同じ物理量になります。
tt(); toSI(Cp`), toSI(Cn`)
===============================
(5.29081721512368e-19*A`*s`, 5.29081721512368e-19*A`*s`)
そんなことが成り立つのは微細構造定数のためです。
微細構造定数と単位電荷
微細構造定数とは下の式で表される無次元の測定値です。プランク定数:h`` と光速度:c と真空の誘電率:ε0 の組み合わせで表されます。無次元の物理定数となります。
ts(); α=eQ`^2/(4pi e0` h`` c`); α jsw`
===============================
0.00729746834685501
微細構造定数の存在は、プランク定数と光速度が 1 の単位系を選択したら、その単位系での素電荷の値が決まってしまうことを意味します。「プランク定数と光速度の二つだけでは長さ・質量・時間の三つの基本単位の組み合わせには自由度 1 が残っている。」にもかかわらずです。実際 PythonSf で、自然単位系での素電荷:eQn・Planck単位系での素電荷:eQp は下のようになります。
tt(); eQn`, eQp`
===============================
(0.302824523103951*Cn`, 0.302824523103951*Cp`)
1/0.302824523103951
===============================
3.3022424662
Planck 単位系・自然単位系どちらも単位電荷は素電荷の 3.302242662 倍の値になっています。実際 3.302242662 の値と微細構造定数 0.00729746748147 は、下の関係にあります。
x=3.302242662; 1/(4pi x^2)
===============================
0.00729746748147
元々微細構造定数は Sommerfeld が発光スペクトラムの微細構造を説明するために導入した物理定数値ですが、その値は単位電荷と素電荷の比という物理的な意味を持っています。h`` c`/m`^2 の物理次元が力の組み立て単位になることから、そのように解釈ですきます。これは下のように機械系の世界と電磁系の世界が 3.3022 の変な数値で相互に関係し有っていると解釈できます。なぜ自然がこんな値を選択しているのかを説明できたらノーベル賞を貰えます。Pauli が死ぬまで微細構造定数を追求し続けたのも良く理解できます。如何でしょうか。
電磁系・機械系世界の 3.3022424662 共存
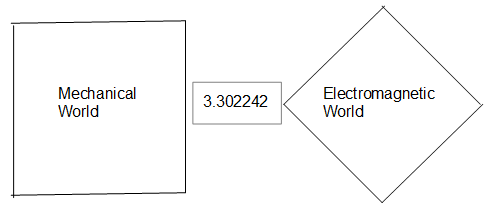
微細構造定数 α が 1/4pi ピッタリであれば、素電荷を定める何らかの自然法則があり、それは光速度とプランク定数とによって説明されるものだとなります。でも微細構造定数が 1/4pi とは 3.302242662^2 だけずれているとしても、素電荷が光速度とプランク定数に依存して説明されるべき物理量であるらしい確率が非常に高いことは残っています。素電荷と光速度とプランク定数は MKS 単位系で互いに無関係に測定された下のような物理定数でした。
ts(); eQ`^2/e0`, h``,c`
===============================
(2.89920463168616e-27*A`*m`*s`*V`, 1.054571628e-34*m`**2*kg`/s`, 299792458.0*m`/s`)
これらの乗除算の組み合わせた数値は 10^-30 から 10^+30 以上の範囲の何処に落ちてもおかしくありません。それが10^-1 から 10^1 の狭い範囲に落ちる確率は 10^-59 以下だからです。ただし α が 1/4pi ピッタリでないことは、光速度とプランク定数以外の何かがないと素電荷を説明できないことを意味します。この何かを示せたらノーベル賞を貰えることは確実です。
L M T に対する電荷の非独立性
長さ:L・質量:M・時間:T に対する電荷の非独立性・すなわち機械系の世界と電磁系の世界が互いに並存可能な組み立て単位を選択していることを、下の次元解析の式で説明できます。
# [L, M, T, C]
[c] = L T^-1 [1, 0,-1, 0]
[h] = L^2 M T^-1 [2, 1,-1, 0]
[eQ^2/(h c)] = L^-3 M^-1 T^2 C^2 [-3,-1,2, 2]
[eQ] = C [0, 0, 0, 1]
mt=~[ [1, 0,-1, 0], [2, 1,-1, 0], [-3,-1,2, 2], [0, 0, 0, 1]]; mt.m_dtrm
===============================
-1.66533453694e-16
自然が、こんな絶妙な関係に単位系を配置していることは単なる偶然ではないと感じます。将来誰かが微細構造定数の説明と一緒に明らかにしてくれるものだと思っています。
実は、sfCrrntIniRelativity.py を実装するとき、この電荷の単位の非独立性に気づいていませんでした。ですから 1 electronVolt を別の違う量にしてやれば素電荷を単位電荷とする単位系が作れるはずだと誤解していました。実際に素電化を単位電荷とする理想自然単位系を誤って実装してしまいました。でも、理想自然単位系を実際に使うと矛盾がどうしても発生してしまいます。それで単位系の次元解析を行ってみて、上の行列式が 0 になることに気づきました。これは強烈な体験でした。これにより、自然が機械系の世界と電磁系の世界が互いに並存可能な組み立て単位を選択していること気付かされました。
その意味で、誤った理想自然単位系のコードを sfCrrntIniRelativity.py に残してあります。興味を持てましたら、下のコードで始まるコメント・アウト・コードも覘いてやってください。
# *****************************************************************************
# **** define ideal Natural units in particle physics h``==c`==kB`== eQ`== e0` == u0` == 1 ****
# *****************************************************************************
# define length:mi`
ε0,μ0 を 1 以外の値にする
自然単位系は、電気定数:ε0,磁気定数:μ0 を 1 にする単位系でした。ε0,μ0 は冗長な四元単位系での単位換算定数にすぎませんでした。でも素電荷を単位電荷に採用しようとすると ε0,μ0 を 0 以外の値にしなければなりません。以下素電荷を単位電荷とする、ε0,μ0 を 1 以外の値にする修正自然単位系を考察します。この単位系は SI 単位系より単純であり、電気定数:ε0,磁気定数:μ0 の意味を浮かび上がらせてくれます。また Heaviside-Lorentz 単位系を考察するとき役立ちます。
ε0,μ0 が本質的には無次元の 1 であり、四元単位系の冗長性ゆえに物理次元を持つことを上で論じました。でも それならば、わざわざ ε0,μ0 の新しいラベルを割り当てる必然性は少いでしょう。 C^2 s^2/(g m^3), g m/C^2 で電磁系の世界と、機械系の世界の冗長な単位間を変換できるというだけにすぎません。
3.3022 * 素電荷を単位電荷とする単位系ならば、e0,u0 定数は 1 になりました。冗長単位系のゆえに電場に D と E, 磁束に B と H の二種類の同じ値ではあるが異なる組み立て単位が導入されてしまうこと説明してきました。
でも素電荷を単位電荷とする自然単位系も欲しくなります。PythonSf では そのような自然単位系を少しだけ修正した修正自然単位系も実装してあります。
修正自然単位系
修正自然単位系は光速度:c とプランク定数:\(\hbar\)と 1 electronVolt と素電荷を 1 となるように基本単位たちを選択した単位系です。修正自然単位系では ε0,μ0 を 1 にできません。逆に言えば、SI:MKSA 単位系で天下りに与えられていた真空の誘電率・透磁率:ε0,μ0 が、この単位系では必然性を持って出てきます。
自然単位系・Planck単位系のように e0n, e0p が 1 となる単位系では ε0,μ0 は単なる単位の換算定数にすぎず、本質的に無次元の 1 でしかありません。ε0,μ0 の新しい変数名を追加する強いモチベーションは生まれません。一方で物理を追求する意味では素電荷を単位電荷とする単位系が欲しくなります。なんせ素電荷が最小単位であり、それの N 倍の電荷量しかありえないのですから。しかし素電荷を単位電荷とする代償として ε0,μ0 の値を 1 に保てなくなります。微細構造定数は \(\hbar\) とc が 1 の単位系ならば、ε0 が 1 のとき、その単位電荷は同じ値にならなければならないことを要求するからです。
sfCrrntIniRelativity.py/sfCrrntIniOpRelativity.py ファイルの中で修正自然単位系での四つの基本単位・組み立て単位を下のように定義しています。接尾辞に k を使って表記しています。
- 基本単位 単位長:mk`, 単位質量:gk`, 単位時間:sk`, 単位電荷:Ck`
- 組立単位 単位エネルギー:elecrok volt:eVk`, 単位力:kk`, 単位仕事:Jk`, 単位電圧:Vk`, 電磁系単位電圧:dVk`, ε0:e0k`, μ0:u0k`, プランク定数(2pi で割った量):hk``, 光速度:ck`
- 素電荷 eQk`
単位長さ・単位質量・単位時間は修正自然単位系・自然単位系どちらでも同じ物理量です。
tt(); toSI(mn`)/toSI(mk`), toSI(gn`)/toSI(gk`), toSI(sn`)/toSI(sk`)
===============================
(1.00000000000000, 1.00000000000000, 1.00000000000000)
tt(); [toSI(mn`),toSI(mk`)], [toSI(gn`),toSI(gk`)], [toSI(sn`),toSI(sk`)]
===============================
([1.97325397334585e-7*m`, 1.97325397334585e-7*m`],
[1.7826759031885e-36*kg`, 1.7826759031885e-36*kg`],
[6.58206676215268e-16*s`, 6.58206676215268e-16*s`])
でも単位電荷・ε0・μ0 は修正自然単位系・自然単位系で異なります。
tt(); [ (Cn`), (Ck`)], [ (e0n`), (e0k`)], [ (u0n`), (u0k`)]
===============================
([Cn`, Ck`],
[Cn`**2*sn`**2/(gn`*mn`**3), 10.904805305561*Ck`**2*sk`**2/(gk`*mk`**3)],
[gn`*mn`/Cn`**2, 0.0917026917931351*gk`*mk`/Ck`**2])
tt(); [toSI(Cn`),toSI(Ck`)], [toSI(e0n`),toSI(e0k`)], [toSI(u0n`),toSI(u0k`)]
===============================
([5.29081721512368e-19*A`*s`, 1.6021892e-19*A`*s`],
[8.854187816e-12*A`**2*s`**4/(kg`*m`**3), 8.854187816e-12*A`**2*s`**4/(kg`*m`**3)],
[1.25663706166589e-6*kg`*m`/(A`**2*s`**2), 1.25663706166589e-6*kg`*m`/(A`**2*s`**2)])
単位電荷は自然単位系でのそれの 1/3.3022 倍だけ小さくなります。ε0 は 1 ではなくなりますが、その物理的意味:「単位電荷が作る機械系世界での表記と電磁系世界での表記のあいだの換算定数」の意味は変わりません。その意味では修正自然単位系での e0k`, u0k` と SI 単位系での e0`,u0` は同じ物理的意味を表現しています。実際 PythonSf 式で下のような関係を確認できます。
# MKSA 単位系に統一してやると下のような物理的比例関係が現れて来ます。
tt(); toSI(Cn`)/toSI(Ck`), toSI(e0n`)/toSI(e0k`), toSI(u0n`)/toSI(u0k`), e0`/toSI(e0k`)/jsw`, u0`/toSI(u0k`) jsw`
===============================
(3.30224246619792, 1.00000000000000, 1.00000000000000, 1.00000000000000, 0.999999999788410)
修正自然単位系での単位力と単位電荷を単位距離だけ離したときの力と ε0
修正自然単位系では素電荷を単位電荷とするので、単位電荷を単位距離離したとき、電荷どうしに働く力は単位力/(4pi)にはなりません。1 さらに e0k` で割ってやった値になります。この力と単位力との比は機械系の世界と電磁系の世界を結びつけていた 3.3022424662 の自乗です。
tt(); gk` mk`/(4pi sk`^2), Ck`^2/(4pi e0k` mk`^2)
===============================
(0.0795774715459477*gk`*mk`/sk`**2, 0.00729746834685502*gk`*mk`/sk`**2)
tt(); (0.0795774715459477*gk`*mk`/sk`**2)/(0.00729746834685502*gk`*mk`/sk`**2)
===============================
10.9048053055609
sqrt(10.9048053055609)
===============================
3.3022424662
修正自然単位系は、自然に存在している素電荷を単位電荷に採用する単位系です。これにより ε0 を天下りにではなく物理的必然として自然に導出できます。
- 光速度\(c\),プランク定数:\(\hbar\)と 1 electronVolt を 1 とする単位系と選択することで、単位長さ:mk、単位質量:gk、単位時間:sk が定まる。その結果単位力:1 gk mk/sk^2 が定まる。
- 素電荷 Ck を単位電荷として採用する。しかし素電荷どうしを単位長さ mk だけ離れた位置に置いたとき、電荷どうしに働く力は単位力(有理化系では 単位力/4pi) と一致しない。
- 冗長ではあるが、三元基本単位:gk,mk,sk の他に素電荷:Ck を基本単位に追加しよう。これにより冗長ではあるが単位系に 1/2 乗が入ってこない、整数べき乗だけによる組み立て単位系を構築でき、機械系の世界と電磁系の世界の両方を記述できそうだ。
- 素電荷を基本単位に追加したことで Ck^2/mk^2 も力を現す組み立て単位になってしまった。残念なことに二つの力 gk mk/sk^2 と Ck^2/mk^2 は力の物理量として一致しない。
- 二つの力の比:真空の誘電率:電気定数:「e0k ≡ 単位力/単位距離だけ離れた素電荷どうしに働く力」を導入しよう。この組み立て単位は無次元であるが、単位の冗長性より (gk mk/sk^2)/(Ck^2/mk^2) ともできる。この e0k ば、電磁系の世界の物理量と機械系の世界の物理量を結びつける比例定数にできそうだ。
- 電気定数:e0k は、形式的には 10.904805305561 Ck^2 sk^2/(gk mk^3) と 1 ではない組み立て単位で表される量だが、「同じ力という物理量を機械系の世界からみた力を電磁系の世界からみた力に換算する」本質的に無次元の 1 の物理量だ。
実際、次のように PythonSf 式で e0k と (Ck^2/mk`^2)/(1gk mk sk^-2/3,3022^2) が、値・単位の両方で同じであることを確認計算できます。
tt(); e0k`, (Ck`^2/mk`^2)/(1gk` mk` sk`^-2/3.3022^2)
===============================
(10.904805305561*Ck`**2*sk`**2/(gk`*mk`**3), 10.90452484*Ck`**2*sk`**2/(gk`*mk`**3))
#### 物理的意味も明確にする SI 単位系での単位電流と μ0 の定義
直前の e0k の導出手順・考え方を単位電流の定義にも使うと、下の SI 単位系での単位電流と μ0 の定義は
電流の単位アンペアは,真空中に1 メートルの間隔で平行に配置された無限に小さい円形断面積を有する無限に長い二本の直線状導体のそれぞれを流れ,これらの導体の長さ1 メートルにつき2 × 10^-7 ニュートンの力を及ぼし合う一定の電流である.これにより,磁気定数μ0(すなわち自由空間の透磁率)は正確に4π × 10^-7ヘンリー毎メートル,すなわちμ0 = 4π × 10^-7 H/m となる.
次のように物理的意味も明確にした定義で構築し直せます。
- 距離 d だけ話して電流 I を流している二本の無限に平行な電線の間には I^2/d に比例する単位長さの力が働きます。
- J. C. Maxwell が実用単位として定めた 1A の電流を流すと、1m だけ離れた二本の平行電線の間には 2x10^-7 N` の力が働きます。これを単位電流の定義にします。(この 10^-7 の係数は emu 単位系での単位電流:「1cmだけ離れた二本の平行電線の間に 2 dyne/cm の力が働く電流」の 10^-1 を1A:実用単位電流としたことから定められました)
- 冗長ではあるが、三元基本単位:kg,m,s の他に単位電流:A を基本単位に追加しよう。これにより冗長ではあるが単位系に 1/2 乗が入ってこない、整数べき乗だけからなる組み立て単位系を構築でき、機械系の世界と電磁系の世界の両方を記述できる。
- 単位電流を基本単位に追加したことで A^2/m も力を表す組み立て単位になってしまった。この力は 2x10^-7 N の力だ。この二つの力は組立単位は異なるが同じ力という物理量を表しているとみなせる。
- この二つ力の単位換算定数 μ0 を導入して磁気定数の名前にしよう。ただし有理化単位系にしたいので平行電線間にはたらく単位長さ当たりの力の公式は 2 μ0 I^2/(4pi d) となるようにしよう。
- 2 10^-7 N == 2 μ0 A^2/(4pi m) なのだから μ0 ≡ 10^-7N/(A^2/(4pi m)) となる。
- 磁気定数:μ0 は pi kg m/(2500000 A^2 s^2) と 1 ではない組み立て単位で表される量だが、同じ単位長さ当たりの力という物理量を、「機械系の世界からみた単位長さ当たりの力を電磁系の世界からみた単位長さ当たりの力に換算する」本質的に無次元の 1 の物理量だ。
実際、次のように PythonSf 式で u0 と 10^-7Newton/(Ampere/(4pi 1meter)) が、値・単位の両方で同じであることを確認計算できます。
ts(); u0`, u0` jsw`, 10^-7N`/(A`^2/(4pi m`))
===============================
(1.2566370614e-6*V`*s`/(A`*m`), 1.2566370614e-6*kg`*m`/(A`**2*s`**2), 1.25663706143592e-6*kg`*m`**2/(A`**2*s`**2))
ただし G. Giorgi が SI 単位系の元になった MKSA 単位系を定めたのは 1902 年のことであり、まだ特殊相対論も量子論もなかった時代です。当然微細構造定数も知られていません。この時代に磁気定数 μ0 を「電磁系での世界の力から、機械系の世界での力への変換定数」として認識するのは無理があります。磁気定数は単なる辻褄合わせによって導いたのだと思います。、実際 G. Giorgi は次のように主張しています。文献 1 より。
Remark.–The magnetic constant of free ether becomes μ0 == 0.000001256 henry/m
Remark.–The electric constant of free ether becomes k_e == 0.000000000008842 farad/m
もし G. Giorgi が μ0 を二つの力の換算定数だと認識していたら、その組み立て単位は henry/m ではなく (kg m/s^2 /m)/(A^2/m) もしくは kg m /(A^2 s^2) としたはずです。
そして SI 単位系規格書での電流の定義は G. Giorgi の電流の定義を踏襲したままなので、上の分かりにくい:辻褄あわせによる単位電流とμ0 の定義になっているのだと考えます。SI 規格書にある単位電流の定義ではなく、「ここでのような物理的意味を伴った単位電流・磁気定数の定義に修正すべきだ」、「誤解を招くだけの「真空の透磁率」の用語は廃止すべきだ」と私は主張します。
PythonSf では pysf\customize.py または pysfOp\customizeOp.py の中で、SI 単位系および SI 単位系で表した物理定数を定義してあります。ただし SI 単位系は MKSA 四元単位系ではなく MKS + AV と電流の他に電圧も基本単位とする五元単位系にしてあります。
回路設計者は L C R 素子とトランジスタを組み合わせて回路を構成します。ここで使われている物理量は電磁系の世界で閉じた物理量です。機械系で必要となる kg を組み立て単位に含まない世界です。質量・時間・電流・電圧:M S A V の四つを基本単位とする組み立て単位の世界です。
電気・回路技術者にとって電圧 V は基本単位であって、SI 単位系で示される kg m^2/(A s^3) のような組み立て単位ではありません。「100 kg m^2/(A s^3) の電圧」といっても電気・回路技術者には通じません。彼らにとっては電圧も基本単位だからです。組み立て単位ではないからです。「100V の電圧」と言わねばなりません。
電気・回路技術者にとって抵抗:Ω は V/A とも表される組み立て単位であって、SI 単位系で示される kg m^2/(A^2 s^3) のような組み立て単位ではありません。「100 kg m^2/(A^2 s^3) の抵抗」といっても電気・回路技術者には通じません。「100V/A の抵抗」と言えば、怪訝な顔はするでしょうが通じます。「100Ωの抵抗」と言ってあげるべきですが。
その他の回路素子でも同様です。コイルは V=L dI/dt の関係で動く素子であり V A/s の組み立て単位を持ちます。コンデンサは V = C ∫I dt の関係で動く素子であり V A s の組み立て単位で表されます。その他の素子も M S V A からなる組み立て単位系の世界で電気・回路技術者は理解しています。電気・回路技術者は kg を含まない MSVA の電磁世界の範囲だけで設計作業を完結させています。エネルギーが関係するときは組立単位 V I の ワット:W またはワット時:W hour で考えます。Joule で考えるのは機械系の世界と交わる特別のときだけです。
kg を含まない MSVA だけで閉じた電磁世界だけで考えている電気・回路技術者に SI 単位系での kg を含んだ組み立て単位を示しても通じません。抵抗・コンデンサ・コイルの単位を下の組み立て単位で言っても通じません。でも これは彼らが抵抗・コンデンサ・コイルを中途半端に理解していることを意味しません。逆に SI 単位系が捻くれているのです。その捻くれた流儀では抵抗・コンデンサ・コイルを理解していないのです。
# 抵抗の SI 組み立て単位
tt(); ut.ohm
===============================
kg*m**2/(A**2*s**3)
# コンデンサの SI 組み立て単位
tt(); ut.F
===============================
A**2*s**4/(kg*m**2)
# コイルの SI 組み立て単位
tt(); ut.henry
===============================
kg*m**2/(A**2*s**2)
ですから PythonSf の単位系は MKSA 四元単位系に、さらに電圧 V も基本単位に追加した MKSAV 五元単位系で実装してあります。 customize.py で定義してあります。 以下のような具合です。
# 抵抗の MKSAV 組み立て単位
ts(); Ω`
===============================
V`/A`
# コンデンサの MKSAV 組み立て単位
ts(); F`
===============================
A`*s`/V`
# コイルの MKSAV 組み立て単位
ts(); uH`
===============================
V`*s`/(1000000*A`)
MKSAV 五元単位系でなければ電気・回路技術者には受け入れられません。
ただし MKSAV 単位系は冗長すぎます。望みの組み立て単位にするためにユーザーが明示的に jsw ≡ Joule/sec/Watt で掛けたり割ったりして単位変換してやらねばなりません。そのような欠点があっても MKSAV 五元単位系にしてやって、やっと実務で使える単位系になります。 kg を持たない MSAV の四元からなる電磁世界だけで閉じた世界において検討・設計を行う電気・回路技術者たちが使える単位系になります。
# 1 coulomb の電荷を 1m だけ話したときの電荷どうしに働く力
ts(); C=A` s`; C^2/(4pi e0` m`^2)
===============================
8987551789.01297*A`*V`*s`/m`
ts(); C=A` s`; C^2/(4pi e0` m`^2) jsw`
===============================
8987551789.01297*kg`*m`/s`**2
# 単位電流がもたらす単位長さ当たりの力
ts(); 2 u0` A`^2/(4pi m`)
===============================
1.99999999994284e-7*A`*V`*s`/m`**2
ts(); 2 u0` A`^2/(4pi m`) jsw`
===============================
1.99999999994284e-7*kg`/s`**2
聞いたことも無い PythonSf の MKSAV 単位系ではなく、権威のある SI 単位系で実装された単位系を使いたければ、sympy.physics.units モジュールを使えます。でも このモジュールを使いこなせるのは
- 電圧,抵抗の組み立て単位 kg m^2/(A s^3), kg m^2/(A^2 s^3) を辻褄あわせでなく基本単位だけから組み立て理解できる
- インダクタンス,磁束密度の組立単位 kg m^2/(A^2 s^2), kg/(A s^2) を辻褄あわせでなく基本単位だけから組み立て理解できる
電気・回路技術者に限られます。そんな技術者はいないと思います。
# SI 単位系での電圧と抵抗
import sympy.physics.units as ut; ut.V, ut.ohm
===============================
(kg*m**2/(A*s**3), kg*m**2/(A**2*s**3))
# SI 単位系でのインダクタンスと磁束密度
import sympy.physics.units as ut; ut.henry, ut.T
===============================
(kg*m**2/(A**2*s**2), kg/(A*s**2))
sfCrrntIniRelativity.py・sfCrrntIniOpRelativity.py には Heaviside-Lorentz 単位系も実装してあります。ただし自然単位系を Heaviside-Lorentz 化したものと、SI 単位系を Heaviside-Lorentz 化したものの二種類だけです。PythonSf では単位の接尾辞 h または l を付けることで、Heaviside-Lorentz 化された単位であることを示します。
自然単位系を Lorentz Heaviside 化した単位系は接尾辞に h を付けて表記しています。単位電荷:Ch,単位電流:Ah, 単位電圧:Vh 単位磁束密度:Th, 単位素電荷:pQh, 電子の電荷:eQh を定義してあります。下のような具合です。
自然単位系を Heaviside-Lorentz 化した;; tt(); `print([Ch`, Ah`, Vh`, Th`, pQh`, eQh`])
[gn`**(1/2)*mn`**(3/2)/sn`,
gn`**(1/2)*mn`**(3/2)/sn`**2,
gn`**(1/2)*mn`**(1/2)/sn`,
gn`**(1/2)/(mn`**(1/2)*sn`),
0.302824523103951*gn`**(1/2)*mn`**(3/2)/sn`,
-0.302824523103951*gn`**(1/2)*mn`**(3/2)/sn`]
===============================
None
SI 単位系を Lorentz Heaviside 化した単位系は接尾辞に l を付けて表記しています。単位電荷:Cl,単位電流:Al, 単位電圧:Vl 単位磁束密度:Tl, 単位素電荷:pQl, 電子の電荷:eQl を定義してあります。下のような具合です。
SI 単位系を Heaviside-Lorentz 化した;; tt(); `print([Cl`, Al`, Vl`, Tl`, pQl`, eQl` ])
[0.178412411615277*10**(1/2)*pi**(1/2)*kg**(1/2)*m**(3/2)/s,
0.178412411615277*10**(1/2)*pi**(1/2)*kg**(1/2)*m**(3/2)/s**2,
0.560499121639793*10**(1/2)*kg**(1/2)*m**(1/2)/(pi**(1/2)*s),
0.560499121639793*10**(1/2)*kg**(1/2)/(pi**(1/2)*m**(1/2)*s),
9.60648476898107e-15*10**(1/2)*pi**(1/2)*kg**(1/2)*m**(3/2)/s,
-9.60648476898107e-15*10**(1/2)*pi**(1/2)*kg**(1/2)*m**(3/2)/s]
===============================
None
実は修正自然単位系を Heaviside Lorentz 化したものも実装してあります。接尾辞に hk` を付けます。ただし、物理的な意味の上では、自然単位系を Heavidide Lorentz 化したものと修正自然単位系を Heaviside Lorentz 化したものは全く同じものに落ち着きます。細かいことを言えば、プログラム上では修正自然単位系を Heaviside Lorentz 化した側に浮動小数点の計算誤差が入り込んできています。
修正自然単位系を Heaviside-Lorentz 化した;; tt(); `print([Chk`, Ahk`, Vhk`, Thk`, pQhk`, eQhk`])
[0.999999999999998*sqrt(gk`)*mk`**(3/2)/sk`,
0.999999999999998*sqrt(gk`)*mk`**(3/2)/sk`**2,
1.0*sqrt(gk`)*sqrt(mk`)/sk`,
1.0*sqrt(gk`)/(sqrt(mk`)*sk`),
0.302824523103951*sqrt(gk`)*mk`**(3/2)/sk`,
-0.302824523103951*sqrt(gk`)*mk`**(3/2)/sk`]
===============================
None
# Ch` の Chk` は同じ電荷量を表す。;; tt(); toSI(Ch`)/toSI(Chk`)
===============================
1.00000000000000
修正自然単位系を Heaviside Lorentz 化した単位系は、Heaviside-Lorentz 化の物理的意味を検討・考察・数値実験するとき有効です。自然単位系との違いは単位電荷だけであり、比較検討を単純化できるからです。
Heaviside-Lorentz 化
ε0,μ0 を持った単位系の Heaviside-Lorentz 化は、それぞれの単位を √(ε0) や √(μ0) で割ったり掛けたりすることで行います。 「D = ε0 E ならば両辺を √(ε0) で割ってやれば」、「B = μ0 H ならば両辺を √(μ0) で割ってやれば」、右辺式と左辺式を同じ組み立て単位の式に変形したことできます。例えば SI 単位系の単位電流は √(ε0) で割ってやることで Heaviside-Lorentz 化された電流値と その組み立て単位になります。下のような具合です。「SI 単位系の 1 A 単位電流は Heaivside-Loretz 化された単位系での単位電流 Al` の 336066.818766 倍と同じ電流量である」といった具合です
# SI 単位系での単位分極密度、単位電場 を Heaviside-Lorentz 化してみる
tt(); D,E=ut.C/ut.m^2, ut.V/ut.m; D/sqrt(ut.e0), sqrt(ut.e0) E
===============================
(149896229*sqrt(10)*sqrt(pi)*sqrt(kg)/(2500*sqrt(m)*s), 250*sqrt(10)*sqrt(kg)/(149896229*sqrt(pi)*sqrt(m)*s))
kg=m=s=1; (149896229*sqrt(10)*sqrt(pi)*sqrt(kg)/(2500*sqrt(m)*s), 250*sqrt(10)*sqrt(kg)/(149896229*sqrt(pi)*sqrt(m)*s))
===============================
(336066.81876646896, 2.9755987326285099e-06)
SI 単位系を Heaviside Loretnz かしたときの単位電場≡単位電圧/単位長さ;;tt(); Vl`/ut.m
===============================
0.560499121639793*sqrt(10)*sqrt(kg)/(sqrt(pi)*sqrt(m)*s)
kg=m=s=1; 0.560499121639793*sqrt(10)*sqrt(kg)/(sqrt(pi)*sqrt(m)*s)
===============================
1.0
分極密度 D を Heavisize-Lorentz 化するとき √(ε0) で割るのならば、電流も Heaviside-Lorentz 化するとき √(ε0) で割ることになります。結果として 1A の単位電流は 336066.818766 Al` SI_Heaviside-Lorentz 単位電流になります。
# SI 単位系での 1Ampere == 336066.818766 Al`
tt(); ut.A/sqrt(ut.e0)
===============================
149896229*10**(1/2)*pi**(1/2)*kg**(1/2)*m**(3/2)/(2500*s**2)
149896229*10**(1/2)*pi**(1/2) /(2500 )
===============================
336066.818766
# 336066.81876646896 Al` == ut.A/sqrt(ut.e0) == ut.A と Al` 電流値を MKS 組立単位:Heaviside Lorentz 単位系で表す
tt(); ut.A/sqrt(ut.e0), Al`
===============================
(149896229*10**(1/2)*pi**(1/2)*kg**(1/2)*m**(3/2)/(2500*s**2), 0.178412411615277*10**(1/2)*pi**(1/2)*kg**(1/2)*m**(3/2)/s**2)
kg=m=s=1; (149896229*10**(1/2)*pi**(1/2)*kg**(1/2)*m**(3/2)/(2500*s**2), 0.178412411615277*10**(1/2)*pi**(1/2)*kg**(1/2)*m**(3/2)/s**2)
===============================
(336066.81876646896, 0.99999999999999933)
上の PythonSf 式を眺めていると、プログラム上では MKSA を基本単位として実装されていた組み立て単位が、下の √(ε0) や √(μ0) で割ったり掛けたりしてやることで電流:A の組み立て要素が調度旨く打ち消しあって MKS だけの三元組立単位に落ち着いてしまうことが見えてきます。これは MKSA 単位系での A が冗長な要素であることを綺麗に示しているとも言えます。
tt(); sqrt(ut.e0)
===============================
250*sqrt(10)*A*s**2/(149896229*sqrt(pi)*sqrt(kg)*m**(3/2))
tt(); sqrt(ut.u0)
===============================
sqrt(10)*sqrt(pi)*sqrt(kg)*sqrt(m)/(5000*A*s)
私には この√(ε0) や √(μ0) で割ったり掛けたりする操作は「中途半端に斜めに見ていために (D,E) または (H,B) とずれて見えていた電磁系の世界を調度真ん中になるような位置に修正してやることで ずれをなくしてやり、一つの単位だけで見える位置に修正してやる」操作に見えます。
Heaviside-Lorentz 単位系では (E,D) が同じ また (B,H) が同じであるだけでなく、E と B も同じ単位になります。特殊相対論的電磁気学で出てくる \(F_{\mu\nu}\) の要素全部が同じ Vl`/ut.m` の単位で表される物理量として表現できます。
tt(); Vl`/ut.m == Tl`
===============================
True
tt(); (Vl` / sqrt(ut.N)) ~== 1
===============================
True
tt(); (Vl` ut.m / Cl`) ~== 1
===============================
True
Heaviside-Lorentz 単位系の四元単位化
Heaviside-Lorentz 化された単位系の組み立て単位に 1/2 べき乗が入り込んでくることに不満を抱く方が大部分だと思います。でもこれは √(単位力) == 単位電圧:√(N)==V の関係を使って MKS+V 見かけ上の四元組み立て単位系にしてやることで、整数べき乗での組み立て単位にできます。
# SI 単位系での √(単位力) == 単位電圧:√(N)==V;; tt(); sqrt(ut.N), Vl`
===============================
(sqrt(kg)*sqrt(m)/s, 0.560499121639793*sqrt(10)*sqrt(kg)*sqrt(m)/(sqrt(pi)*s))
kg=m=s=1; 0.560499121639793*sqrt(10)*sqrt(kg)*sqrt(m)/(sqrt(pi)*s)
===============================
1.0
# 自然単位系での √(単位力) == 単位電圧:√(N)==V;; tt(); N=gn` mn`/sn`^2; sqrt(N), Vh`
===============================
(sqrt(gn`)*sqrt(mn`)/sn`, sqrt(gn`)*sqrt(mn`)/sn`)
# 修正自然単位系での √(単位力) == 単位電圧:√(N)==V;; tt(); N=gk` mk`/sk`^2; sqrt(N), Vhk`
===============================
(sqrt(gk`)*sqrt(mk`)/sk`, 1.0*sqrt(gk`)*sqrt(mk`)/sk`)
ただし、ここでの MKS+V は「MKS に冗長な基本単位 V を追加した四元単位系」ではなく「Heaviside Lorentz 三元単位系の √(N) を V に置き換えた見かけ上の四元単位系」です。冗長な四元単位系のときのように基本単位 V を自由に選択できるわけではありません。本質的には冗長性の無い三元単位系のままです。
Heaviside-Lorentz 単位系での抵抗の組み立て単位は 1/速度 ではなく無次元の 1?
(注意! ここでの考察は通常の教科書には書かれていないことです。でも特殊相対論を時空幾何学として統一して理解できている方には同意してもらえると思います)
Heaviside-Lorentz 三元単位系(Gauss 単位系でも同じです) では、抵抗の三元組み立て単位が 1/速度 になってしまいます。でも この 1/速度 になるのは光速度が入り込んできてしまったためです。電流を ∂t(電荷) で定義したためです。
電流を特殊相対論の時空幾何学で統一して考えてやったときの 電流定義:∂ct(電荷) を採用してやれば 抵抗≡電圧/電流の組み立て単位は無次元になります。このことから Heaviside-Lorentz 単位系での抵抗の組み立て単位が 1/速度 になるのは光速度が入り込んだためだと結論できます。
しかし物理法則の対称性を追求する意味では 電流定義:∂ct(電荷) を採用すべきだと思いますが、そうすると Heaviside-Lorentz 単位系ではなくなってしまいます。教科書に書いてある Heaviside-Lorentz 単位系ではなくなってしまいます。無用な混乱を招きます。
Heaviside-Lorentz 単位系が定まったのは相対論が出てくる直前ですから、まだ時空幾何学までを見据えた単位系にできなかったのは理解できます。仕方ないことだと思います。PythonSf でも、この歴史的経緯に妥協した、抵抗の組立単位が 1/速度になる Heaviside-Lorentz 単位系で実装してあります。下の 1/c J 含んだ Maxwell 方程式に合わせてあります。
電磁系・機械系世界の共存と Maxwell 方程式
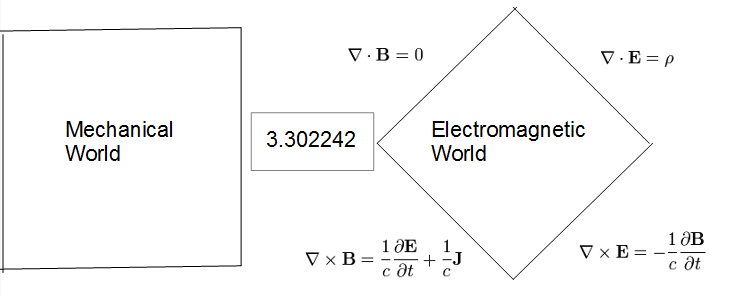
Heaviside-Lorentz 単位系と壮大に捻くれた MKSA 単位系
Heaviside-Lorentz 単位系を扱えるようになると、長さ・質量・時間:MKS の三つの基本単位と電流(もしくは電荷) の基本単位は独立して選べないことが分かります。電磁系の世界を、より単純した形式で理解可能になります。「自然単位系を Heaviside-Lorentz 化した単位系」と「修正自然単位系を Heaviside-Lorentz 化した単位系」とが同じ単位系に落ち着いてしまうことが、それを強く暗示しています。
長さ・質量・時間:MKS 三つの基本単位により機械系の世界での単位力と その組み立て単位が定まります。電磁系の世界での単位力:単位距離だけ離れた単位電荷の間には、この単位力と同じ力が(有理化系では単位力/(4pi) の力になる)働くように単位電荷を定めてやらないと機械系の世界と電磁系の世界の整合性がとれなくなります。
自然単位系では、機械系の単位力と電磁系の単位力が同じ力が同じになるように基本単位電荷を選択し、MKS+C 単位系を構築しました。冗長な四元単位系のせいで e0n,u0n は無次元ではなくなってしまいましたが。でも その単純性の故に
- e0n の無次元性:機会系の単位力と電磁系の単位力の比であること
- u0n が 1/光速度の次元を持つ(Maxwell 方程式で、明示的に 1/c を出してやることで u0n の次元を 1 にできる)ことが
が理解可能でした。 (逆に機械系の単位力と、単位距離だけ離れた電線間に働く力を同じになるように基本単位電流を選択してやれば、u0 を 1 とし e0 を 1/光速度とする単位系を構築できました。)
このような機械系の単位力と電磁系の単位力が同じ力が同じになる単位系を選択してやれば
- 物理的には同じものである真空中の (E,D), (B,H) は、単位系の冗長性の故に組み立て単位が異なるけれど同じになること
- e0,u0 が本質的に無次元の 1 であること
を容易に汲み取れる単位系にできました。
e0,u0 が 1 ではない四元単位系であっても、それを Heaviside-Lorentz 化してやれば、機械系の単位力と電磁系の単位力が同じ力が同じになる三元単位系を構築できました。物理的には同じものである真空中の (E,D), (B,H) は全て同じ Volt≡√(単位力)の単位量に落ち着きました。ただし捻くれ具合が少なくなりすぎて、閉じた MSAV の電磁系だけで理解している技術者には、Heaviside-Lorentz 単位系は理解・扱いが困難な単位系になってしまいました。
この意味で捻くれ具合は Heaviside-Lorentz 単位系 < 自然単位系 < SI MKSA の順序で酷くなっています。SI MKSA 単位系は閉じた旧来の MSAV の電磁系だけで理解している技術者に妥協しすぎたために壮大に捻くり回されすぎた単位系になっています。 e0,u0 を 1 にできなくなっています。真空の誘電率・透磁率のせいで電磁気学の諸概念が無用に難しくなっています。にもかからわらず、SI:MKSA 単位系が捻くれていることを指摘している教科書が殆どないことを憂えています。e0,u0 が本質的に無次元の 1 であることを理解していないもののほうが多数派なのが現実です。そのために この論考を書いています。
## emu:三元単位系と MKSA:四元単位系
emu(cm,g,s) ←→ MKSA(m,kg,s,A)
MKSA 単位系は冗長な単位系
自然単位系、プランク単位系では、単位電荷が物理的対象物として現れる。SI 単位系でのように人為的に定義する必要が無い。 –>
SI 単位系は歴史的な経緯に妥協したことで定まっている単位系だと よく言われます。でも どのような経緯に どのように妥協したのか、明示的に書かれていません。以下 この経緯と妥協について記述します。
電磁単位系に関連する年表
まず下に電磁気に関する年表を示します。19 世紀は Volta の電推から始まって 105 年間に モールス通信、Maxwell 方程式、電話、エジソンの白熱電球、発電機、電子の発見、特殊相対論まで突き進んだ凄まじい進歩・変革の時代でした。
| –西暦— | —-出来事———————————————————————————— |
|---|---|
| 1800 年 | Volta の電推 |
| 1804 年 | 蒸気機関車の発明 |
| 1812 年 | Napoleon メートル法 |
| 1826 年 | Ohm の法則の発表 |
| 1831 年 | M. Faraday の電磁誘導の法則 |
| 1833 年 | F. Gauss が absolute 単位系を 論文(※1)で提唱した。 |
| 1835 年 | モールス信号と電信線を使った交信が始まった |
| 1836 年 | ダニエル電池の発明 |
| 1858 年 | 一回目の大西洋横断海底通信ケーブルを布設で単位の計算間違いにより失敗(※2) |
| 1863 年 | 敷設失敗を受け、英国政府が J. C. Maxwell を中心に emu 単位系と実用単位系(※3)を定めさせた |
| 1861 –65 | 南北戦争 |
| 1865 年 | Maxwell 方程式の発表 |
| 1867 年 | 明治維新:大政奉還 |
| 1872 年 | BAU が抵抗の単位を `ohm と呼ぶことにした。 |
| 1876 年 | A.G, Bell と E.Gray が電話を発明した |
| 1879 年 | エジソンが白熱電球を発明した |
| 1881 年 | absolute/practical system of units が FICE(※4) で定められ五つの単位(※5)が承認された |
| 1882 年 | エジソンの電力システムが稼動を始めた。 |
| 1889 年 | Second International Congress of Electricians で joule, wattの単位が承認された。 |
| 1892 年 | ウェストン標準電池 1.0183`volt at 20 celsius |
| 1892 年 | BAU が電流の silver ampere 定義を定めた |
| 1892 年 | O. Heaviside が有理化単位系を提唱 |
| 1892 年 | Lorentz 力を含む論文を H.A Lorentz が発表した |
| 1893 年 | international ohm(※6)/volt(※7) を定めた。 |
| 1897 年 | J.J. Thomson が電子を発見した |
| 1900 年 | Planck 定数が発表された |
| 1902 年 | Giovani. Giorgi が MKS に R を追加した四元有理化電磁単位系を提唱した |
| 1903 年 | ライト兄弟による飛行機の発明 |
| 1904 年 | 力の単位 newton が Robertson によって提案される |
| 1905 年 | 特殊相対性理論の発表 |
| 1916 年 | 微細構造定数を Sommerfeld が導入した |
| 1948 年 | SI(International System of Unit) μ0:4π 10^-7 H/m を定める(※8) |
| 1960 年 | SI(International System of Unit) 単位系が定められる |
- ※1 “Intensitas vis magneticae terristis in mensuram absolutam revocata.”
- ※2 ただし抵抗・電圧・電流の単位が定まっておらず計算間違いで一回目の大西洋横断ケーブルの敷設は失敗した。このためイギリス政府が Mawell に実用単位を定めることを依頼した。
- ※3 BAU(Britsh Association Unit) と呼ばれた実用単位系:単位電流・単位電圧を 10^8abvolt/10^-1abampere と定めた。ここで 単位電圧:10^9abvolt 単位電流:1abvolt と決めていれば μ0を 1 にできた。Pt-Ag 合金を使って emu 単位抵抗の10^9 倍 ≡ 1 ohm の practical な意味の標準抵抗を定め配布した。
- ※4 FICE:First International Congress of Electricians
- ※5 五つの単位: volt, ohm, ampere, coulomb, farad
- ※6 international ohm: 重さが 14.4521gram で、長さが 106.3cmの水銀の 0 度C における抵抗 1Ω を定めた。
- ※7 international volt: (15度C で Clark セルが 1.434`volt) を定めた。
- ※8 ε0,μ0 真空の誘電率・透磁率 電気定数・磁気定数
実用単位の策定と SI 単位系
この年表で「1858 年:一回目の大西洋横断海底通信ケーブルを布設失敗」と「1863 年 J. C. Maxwell が中心となり emu 単位系と実用単位系定めた」ことに御注目ください。
大西洋横断海底通信ケーブルの敷設は、アメリカとイギリスの間を電線でつないで、モールス符号通信を可能にするために行われました。でも この敷設工事は失敗でした。通信線の抵抗値が高すぎて、リレーを駆動できませんでした。まだ電圧・電流・抵抗の単位さえ定まっていなかったことによる計算間違いが原因でした。
これに懲りたイギリス政府は J. C. Maxwell に合理的な電圧・電流・抵抗の単位を定めるように依頼しました。元々 J. C. Maxwell は emu 単位系を定めていました。でも電磁気学を基にした emu 単位系は、オームの法則:V=R I で設計している技術者には難しすぎました。さらに加えて emu 単位系での単位電圧・単位抵抗は、通信線の敷設で使う電圧や抵抗の値とは 掛け離れすぎていました。電流値は近かったのですが。 そのため J. C. Maxwell は emu 単位系での単位電圧の 10^8倍、単位抵抗の 10^9 倍、単位電流の 10^-1 倍を実用単位とすることにしました。当時の通信線で使っている電圧・抵抗・電流値に近くなる、かつemu 単位量の 10^N 倍となる物理量を選択しました。実際に Pt-Ag 合金で 1Ω の単位基準抵抗を作り配布までしました。もともと Ohm,Volt,Ampere の意味は 現在の「ギガ」のような 10^9, 10^8, 10^-1 倍の意味だったそうです。
ただし、ここで J. C. Maxwell は痛恨のミスをしています。通信線の電圧、電流に合わせるのと同時に、欧米での三桁ごとの数値呼称にも合わせるべきでした。emu 単位抵抗の 10^9倍を実用単位抵抗・, emu 単位電流の 10^0==1 倍を実用単位電流とすべきでした。J. C. Maxwell が実用単位抵抗・電圧・電流を このように 10^(3N) 倍と切の良い値に定めていたら、SI 単位系でも μ0 を 1 とする単位系を選択できました。cm, gram, second を基本単位とする単位系を使い続けられました。理論的にすっきりとした emu 三元単位系に単位電流を追加した emu 四元単位系または gauss 単位系を選択できました。1 absolute_Ampere == 1 practical_Ampere, 1 Giga absolute_Volt == 1 proctical_Volt, 1 Giga absolute_Ω == 1 practical_Ω の二つの単位を並立させられました。電気・回路技術者たちが使う practical な MSVA 四元単位系と、理論物理学者が使う Gauss 単位系を両立させられました。
たぶん J. C. Maxwell も 10^9倍・10^0 倍を単位電圧・単位電圧にするか迷ったはずです。そのほうが自分が普段使っている emu 単位系との換算が楽になるからです。ここで一桁違ったとしても、当時の通信技術者たちが慣れ親しんでいる通信ケーブルでの電圧・電流との違いは問題になるほどではありません。でも大西洋横断海底通信ケーブル敷設の失敗を考慮しすぎたのでしょう。通信ケーブルで使っていた抵抗値・電流値・電圧値に近くすることを最優先としたのでしょう。しかし e0,u0` の物理定数が導入され、それらが本質的に無次元の 1 であることを理解されていない事実をみたら、J. C. Maxwell も 10^9 倍の電圧、10^0 倍の電流を practical な単位として選択すべきだったと同意してくれると思います。
ちなみに あまり知られていませんが MKSA 単位系は emu 単位系は良く似ています。emu 三元単位系を電流値も基本単位とする四元単位系に修正するだけで、単位系の構造は MKSA 単位系と殆んど同じになります。
実際 SI 単位系での u0/(4pi) が下のように 10^7 と変な値になっているのは emu 単位系での単位電流の 10^-1 倍を実用単位電流に J. C. Maxwell が定めてしまったからです。
ts(); u0`/(4pi)
===============================
9.99999999971418e-8*s`*V`/(A`*m`)
10A:emu単位系での単位電流を流した、1cm 話れた平行電線 1cm 当たりに働く力は 2 dyne であることを下のように SI 単位系の計算で確認できます。
ts(); R,δl,I=1cm`,1cm`, 10A`; u0`/(2pi) I^2/R δl jsw`
===============================
1.99999999994284e-5*kg`*m`/s`**2
ts(); dyne=1gram` cm`/s`^2; R,δl,I=1cm`,1cm`, 10A`; u0`/(2pi) I^2/R δl jsw` /dyne
===============================
1.99999999994284
CGS ではなく MKS 単位系になった理由
先行していた CGS 単位系を押しのけて MKS 単位系が優勢になった理由は、J. C. Maxwell が emu 単位系での単位電圧の 10^8倍、単位抵抗の 10^9 倍、単位電流の 10^-1 倍を実用単位とすることにしたからです。抵抗・電流・電圧の実用単位系と cm,gram,secont 単位を組み合わせると、モータが発生するトルクや抵抗の発生するエネルギー:V I==W s との間に不必要な換算定数が必要になるからです。しかも その換算定数は電磁系物理量ごとに変わってくるのですからたまりません。
年表を眺めていると、モータや発電機など機械系と電磁系とを組み合わせた装置の発展共に MKS 単位系が広く使われていくことが見えてきます。上の年表に書かれていないことを追加していけば、この説がより補強されるでしょう。
実用単位系では 1A * 1V == 1W になります。この単位時間値の電磁系エネルギー 1W に対応する機械系の単位時間当たりのエネルギーは 1 N m/s== 1 J/s == 1 kg m^2/s^3 ですが、CGS 単位系では余分な 10^7 N m/erg の比例係数を付けなければなりません。
ts(); 1.0W`/(1.0 gram` cm`^2/s`^3), 1.0W` J`/s`/W` /(1.0 gram` cm`^2/s`^3)
===============================
(10000000.0*A`*s`**3*V`/(kg`*m`**2), 10000000.0000000)
ts(); 1.0W`/(1.0 kg` m`^2/s`^3), 1.0W` J`/s`/W` /(1.0 kg` m`^2/s`^3)
===============================
(1.0*A`*s`**3*V`/(kg`*m`**2), 1.00000000000000)
「重厚長大産業の発展とともに MKS 単位が使われるようになった」とする説明が散見されますが、これは誤りです。重厚長大といっても機械系は mm で図面を書きます。最低でも 0.1m精度の公差に収まらないと、機械系はまともに動かないからです。しかも機械系などの部品で kg 以下を 0 にできるものは、殆んどありません。さらに言えば機械系の図面に書かれるのは mm 寸法と形と材質がメインです。重量は結果として定まるだけで、設計図面に重量まで書かれることは殆んどありません。1A * 1V = 1W の条件がなければ kg で書こうが g で書こうがたいした違いはありません。ですから「重厚長大産業が MKS 単位を必要とした」とするのは誤りです。
もし Maxwell が「emu 単位系での単位電圧の 10^9倍、単位抵抗の 10^9 倍、単位電流の 10^0 倍を実用単位とする」ことにしていたら、現在でも CGS 単位系が主流だったでしょう。V や Ω は基本単位の 1ギガ倍の値の実用単位となったでしょう。現在のトンの単位のような扱いになっていたでしょう。
そうなっていれば、μ0 の値は 1 となり電磁気学の記述・学習が簡単になったでしょう。四元単位系の冗長性など自然単位系まで持ち出して説明することなく簡単に見通すことができたでしょう。真空の透磁率の物理的意味で、不必要な回り道を辿らずに済んだでしょう。歴史に「たら れば」を言っても無駄なのは承知していますが、Maxwell が実用単位を定めるのに 電圧:10^9 倍と 電流:10^0 倍を選択しなかったことは非常に残念です。
G. Giorgi が提唱した単位系
SI:MKSA 単位系は、イタリアの電気技術者 G. Giorgi が提唱した単位系です。でも辻褄合わせの単位系です。彼は電磁気学の理論展開に従って単位を組み立てていくことには興味を抱いていません。
ここ*1の付録に 1904 年時点で G. Giorgi が提唱していた MKSA 単位系が纏められています。 ここで下のことに注目すべきです。(ただし この節の内容は、この論文から推測しているだけです。誤解がある可能性も高くなっています。誤りがあったら御指摘ください。)
- 電圧 kg m^2/(A s^3), 抵抗:kg m^2/(A^2 s^3) 抵抗の組み立て単位が出てこない
- ohm または ampere どちらかを四つ目に負荷する基本単位としている。一つに絞っていない。
- μ0 が 磁気定数:magnetic constant になっている。vacumm permeability ではない。
- ε0 が 電気定数:electric constant になっている。vacumm permittivity ではない。(ε0 は k0 になっているが、これは本質的な話ではない)
- すでに weber, henry といった単位も提唱されており、磁気系も含めて提唱された単位系になっている。
「この G. Giorgi の論文に電圧 kg m^2/(A s^3), 抵抗:kg m^2/(A^2 s^3) 抵抗の組み立て単位が出てこない」ことは基本単位から組立単位全てを電磁気学の展開に従って導出する」ことを G. Giorgi は追求していないのだと推測します。MKS 単位系と辻褄の合う電磁単位系を提唱しているにすぎないと私は解釈しています。
抵抗を基本単位として許していることは、組み立て単位系に 1/2 乗が入り込んでくることを意味します。そんなことは G. Giorgi にはどうでも良いことだったはずです。G. Giorgi には電磁系の世界と機械系の世界が並存しているとの自然認識はなかったはずです。まだ特殊相対性理論も量子力学も微細構造定数もない時代ですから当然ですが。
ε0,μ0 真空の誘電率・透磁率 電気定数・磁気定数
真空の誘電率・透磁率の用語が無用の混乱を招いているので、SI:MKSA 単位系でも G. Giorgi が最初に提案した名称:電気定数・磁気定数の用語に戻そうとしています。でも それだけでは不十分です。ε0,μ0 の物理的意味の説明を追加すべきです。
Vacumm permiability の wikipedia では次のように説明しています。
The parameter μ0 is a measurement-system constant, not a physical constant that can be measured. It does not, in any meaningful sense, describe a physical property of the vacuum. This is why the relevant Standards Organizations prefer the name “magnetic constant”, rather than any name that carries the hidden and misleading implication that μ0 describes some physical property;;http://en.wikipedia.org/wiki/Vacuum_permeability
拙訳:パラメータμ0 は計測体系中に出てくる定数にすぎません。実際に計られる物理量ではありません。いかなる意味でも μ0 は真空の物理的意味を記述するものではありません。主だった標準委員会は、μ0 の用語として物理的意味を暗示しない磁気定数の用語を選んでいます。
「パラメータμ0 は計測体系中に … μ0 は真空の物理的意味を記述するものではありません。」には同意します。ならば μ0 はいったい何なんだとなります。磁気定数などういう、G. Giorgi が昔導入した言葉に戻しても μ0 の説明にはなりません。「真空の透磁率」の言葉による誤解を少し防ぐだけです。
物議を醸すのは承知で、この wikipedia の説明を私流に言い直すと下のようになります。こちらの方が より明確です。如何でしょうか。
真空の誘電率・透磁率の用語は、電磁気学の初学者を「真空の誘電率・透磁率とは何なんだ」と悩ませます。自分 が分っていないことに対する感性の高い学生ほど悩まされます。一方で「真空の誘電率・透磁率とは何なんだ」と悩むことなく電磁気学の教科書を辻褄合わせだけで理解したとする者も多く輩出します。「ε0,μ0 は、本質的に物理次元の無い、しかし機械系の世界と電磁系の世界の間を橋渡しする率:rate である」ことまで理解できる学生は殆どいません。この問題を少しでも避けるため、真空の誘電率・透磁率の用語を電気定数・磁気定数に変更する動きになっています。
上の ε0,μ0 の説明文章たちは殆ど否定文だけであり、μ0 が物理的に何であるかは積極的に説明していません。Web page にある説明も似たような説明ばかりで μ0 の物理的意味を明示的に説明しません。先に論じたように μ0 の物理的な意味を説明できるのに。肯定文で下のようにε0,μ0 の意味を積極的に説明すべきです。
基本単位:MKS に A:単位電流を基本単位として追加すると、単位系としては冗長な単位系になってしまう。Gauss 単位系、emu 単位系など MKS だけから電磁単位系を構築できていたのですから。それでも MKSA 四元単位系にする理由は、整数べき乗だけの組み立て単位系にできるからです。 1/2 のべき乗の項が出てこなくできるからです。
でも冗長な単位系にすることで一つの物理量を複数の組み立て単位で表せてしまいます。力の組み立て単位を K M S^-2 とすると同時に、クーロンの法則からも力の単位を組み立てられます。 (A S)^2 M^-2 も力の組み立て単位になってしまいます。ε0 は、この二つの組み立て単位の間の換算定数です。ですから ε0 は (A S)^2 M^-2/(K M S^-2)==A^2 S^4 K^-1 M^-3 の組み立て単位を持ちます。同様に μ0 は二本の電線の間に働く単位長さ当たりの力の換算定数であり (K M S^-2/M)/(A^2/M)== K M^- S^-2 A^-2 の組み立て単位を持ちます。。
このような ε0,μ0 の説明文を SI 単位系の規格書の最後に追加すべきだと私は主張します。皆様はどう考えますでしょうか?
最後に
本論考で以下のことを考察してきました。
- SI 単位系での電流定義はここでのように、基本単位の冗長性と組立単位の二重性を明示する形式で書き直すべき
- e0,u0 は人間の都合:歴史的経緯で導入された物理定数であり本質的に無次元の 1 の値だ。SI:MKSA 単位系の策定者たちは、既に実用単位系:MSVA の閉じた電磁系の世界だけで考察・設計をしている電気・回路技術者たちに妥協して、e0,u0 を 1 としない単位系を選択した。その代償として、真空中では同じであるべき E,D B,H が別の 値・組み立て単位になってしまっている。その意味で SI:MKSA 組み立て単位系は壮大に捻くれている。
- そんな捻くれた電磁気学になってしまう単位系を敢えて選択しなければならなかった理由は、J. C. Maxwell が実用単位系を定めたとき、emu 単位系での単位抵抗の 10^9 倍、 単位電圧の 10^8倍、単位電流の 10^-1 倍を選択したためだ。大西洋横断ケーブル敷設の計算間違いでの失敗に配慮しすぎて、単位電圧:10^9倍、単位電流:10^-0 倍を選択できなかったためだ。この おっちょこちょい な技術者がいなかったら、今でも e0,u0 が無次元の 1 の cgs 単位系が使われていたはず。
そうであったならば、機械系の世界と電磁系の世界が斜めに交わっているところまで、多くの電気・回路技術者に理解されていたはずです。皆様には納得してもらえましたでしょうか?
なお、このような規模の大きな単位体系の考察には、PythonSf one-liners での数値実験での積み重ねが必須です。皆様も自分の手を使って数値実験を繰り返して、電磁気の世界を楽に・早く・正しく理解してください。 この文章もしくは sfCrrntIniRelativity.py/sfCrrntIniOpRelativity.py に誤りがありましたら教えてやってください。 ただし具体的な どのように誤っているのかを PythonSf 計算式で、数値実験可能な誤りとして御指摘ください。
■■ 参考 URL
blog comments powered by Disqus