Pythonsf Calculations On Editors Supporting tagline
##■■ 概要 エディタのカーソル下の文字列をは計算式と看做して実行できると便利です。 PythonSf は、そのような計算に特化した script language です。
もっとコンピュータ・パワーを活用しましょう
電卓を叩きながらシミュレーション・ソフトを開発している方たちを、よく見かけます。
##■■ theme エディタのカーソル下の文字列を OS コマンド または計算式と看做して実行できると便利です。 PythonSf は、そのような計算に特化した script language です。標準配布状態で大学の学部数学程度までの計算が可能です。
↑cf. Emacs shell mode ↑ 話を単純化して OS を除き、計算式だけにする
エディタを Matlab, Mathematica 以上の計算環境に! 使い慣れたエディタから「コンピュータの操作コマンド入力と実行」「計算式の入力と実行」が可能なことが望まれます。 テキストの編集操作にはエディタが適しています。そしてコンピュータ操作、計算式 コンピュータを使って何かを創造するのならば GUI ではなく CUI を選択すべき
現在のコンピュータを前提とした計算環境 ↑ Matlab, Scilab, Maxima などでも不満。 ↑ それらのソフトを起動しておかねばなりません。
計算式の記述はプログラミングではありません。→ 計算に適した記述とプログラミングに適した記述は異なります。 → PythonSf は計算式の記述に特化したスクリプト言語です。
PythonSf 式中に self が出てくることはない
計算式の記述は最小の労力で行われるべき。 決まりきった import numpy 文は省略すべきです。 ↑思考を妨げてはならない。 一秒でも早く次の段階に移りたい ↑ 自分自身がみるためのグラフ作成に飾り立てるためのパラメータを渡すべきではない ↑ Mouse を使うなど論外 微分・積分記号を入力するのにマウスを使っていられません → エディタの使用 → エディタ上で実行まで完了する
sklearn sfCrrntIni.py の例
PythonSf で作成するのは実行可能な計算式です。プログラム・コードではない。 if then else 文を書くことはない PythonSf 式中でクラスを作成することはない → one-liner の多用
↑ OS コマンド実行環境は書かない これ単独で別記事にすべき ↑ Python 環境としての PythonSf も別に書く 一行程度で言及することはあり
##■■ 概要 PythonSf ではエディターのカーソル下にある一行またはコード・ブロックを PythonSf 数式とみなしてプリプロセッサ処理して Python コードに直し、そのコードを動かして計算させます。標準出力に返された結果をエディタの最下段に表示します。同時に、その文字列をエディタの・コピー・ペースト・バッファにも記録します。具体的な計算の様子を youtube PythonSf introduction 1/3, PythonSf introduction 2/3, PythonSf introduction 3/3 で確認ください。
エディタに上の動作をさせるため、pysf.vim, pysf.el といったエディタ・マクロを組み込んだ状態で使います。現在のところ vim と emacs ののマクロを用意しています。
このマクロは、カーソル下の一行を OS コマンドとして実行したり、カーソル下のブロック・コードを任意言語のコードとしてコンパイル・実行させることも可能です。
##■■ 数式に近い PythonSf 式 PythonSf では、エディターで書く数式文字列を数学の教科書にある数式にできるだけ近づけています。プロプロセッサにより これを可能にしています。プリプロセッサにより以下のことを行っています。
- Python 言語の名前空間を拡張してあり、前後に逆シングル・クォート記号:` を付けた変数を使えます。これにより `X,`Y といった、短くても Python 変数と衝突しない数学変数を使うことを可能にしています。
- Python 2.7 でも漢字のギリシャ文字と漢字記号∂∇□△を使えます。
- カレント・ディレクトリにある sfCrrntIn.py と pysf/customize.py (オープン版では sfCrrntIniOp.py と pysfOp\customizeOp.py) の二つを from .. import * してから、プロプロセッサ処理された PythonSf 計算式を実行します。customize.py で sin などの基本関数を既に import してあり また `X,`Y に恒等関数を割り当ててあるので、宣言や import 文なしで sin や `X,`Y を使えてしまいます。
PythonSf の基本関数 exp, sin, cos, tan, sinh, cosh, tanh, arcsin, arccos, arctan, log, log10, sqrt, absF と `X,`Y,`Z,`T 恒等関数は加減乗除べき乗算および関数合成が可能です。ですから \(sin(\frac{1}{x}+3y)\)の \((\pi,\frac{\pi}{3})\) における値は下の PythonSf 式で計算できます。
# PythonSf 式と その計算
sin(1/`X+3`Y)(pi, pi/3)
===============================
-0.312961796208
sin(1/`X+3`Y)(`π, `π/3)
===============================
-0.312961796208
# Open 判ではプリプロセッサが貧弱なので積演算子の省略ができません。
sin(1/`X+3*`Y)(pi, pi/3)
===============================
-0.312961796208
sin(1/`X+3*`Y)(`π, `π/3)
===============================
-0.312961796208
より複雑な計算式
複数の PythonSf 式、Python 式/文を ; デリミタで区切って並べた PythonSf 式も使えるので、より複雑な計算も PythonSf ワンライナー式で扱えます
# シンボリック微分: sin(1/x)
# PythonSf commercial 判
ts(); ∂x( ts.sin(1/`x) )
===============================
-cos(1/x)/x**2
# PythonSf open 判
ts(); x=ts.Symbol('x'); ts.diff( ts.sin(1/x), x)
===============================
-cos(1/x)/x**2
# Groebner 基底をシンボリックに計算する
# PythonSf commercial 判
ts();x,y,z=ts.symbols('x y z');f1,f2,f3=[x+y^2+3z^2-4, 4y^2-5,y^4-5z-10]; ts.groebner([f1,f2,f3], [x,y,z])
===============================
[-5/4 + y**2, 1483/256 + x, 27/16 + z]
# PythonSf open 判
ts();x,y,z=ts.symbols('x y z');f1,f2,f3=[x+y**2+3*z**2-4, 4*y**2-5,y**4-5*z-10]; ts.groebner([f1,f2,f3], [x,y,z])
===============================
[256*x + 1483, 4*y**2 - 5, 16*z + 27]
上の PythonSf 式で ts() 関数は sympy package をインポートし ts 変数に割り当てる関数です。同時に `x,`y,`z,`t 変数に sympy symbol を割り当ています。customize.py に実装してあります。ts() を呼び出すだけでシンボリックな数式処理が可能になります。
もちろん行列 ベクトル演算も得意です。
# 行列とベクトルの積演算
# |1,2| * |5| 1/|1,2| * |5|
# |3,4| |6], |3,4| |6]
# PythonSf commercial 判
mt,vc=~[[1,2],[3,4]], ~[5,6]; mt vc, mt^-1 vc
===============================
(ClTensor([ 17., 39.])
, ClTensor([-4. , 4.5])
# PythonSf open 判
mt,vc=np.matrix([[1,2],[3,4]]), np.matrix([5,6]).T; mt*vc, np.linalg.inv(mt)*vc
===============================
(matrix([[17],
[39]]), matrix([[-4. ],
[ 4.5]]))
以下 面倒なので PythonSf open 判のコードは省略します。要は一部の例外を除いて Python 文法の範囲で記述する」ということです。バック・クォートを使った名前空間の拡張や漢字ギリシャ文字の使用などが、その一部の例外です。
##■■ PythonSf ワンライナー 以上のように短い数式記述ができる PythonSf ではワンライナー記述を多用します。各自の専門分野に合わせて sfCrrntIni.py ファイルを適切に作り上げれば、日常計算の 90% 以上をワンライナー計算で済ませられるでしょう。
分野を限定すれば Python コードに必要な import 文は限られます。多用する関数も限られます。それらをカレント・ディレクトリの sfCrrntIni.py に書いておけば、PythonSf ワンライナーにはエッセンスだけを書いていけます。
線形代数など、数学者が完成してくれた数学体系での PythonSf 計算は、多くの場面で if then else 構文で場合分けすることなく、クラス・インスタンスを作りメソッドを働かせる作業の繰り返しになります。Python コードで書くならばインデントなしで数学計算処理ができてしまうことのほうが多いでしょう。インデントなしのコード・ブロックならば、それを横に並べてワンライナーにしても可読性の低下は少しで済みます。ワンライナーには少しの可読性の犠牲はありますが、それを補ってあまりある数式ハンドリングの容易さがあります。結果としてワンライナーを多用することになります。
PythonSf でワンライナーに拘るのは、ワンライナーは その一行だけで完結するからです。前後の文脈の影響を受けないからです。任意のワンライナーを自由に別のファイルにコピー・ペーストできるからです。ワンライナーに影響を与える前提条件は sfCrrntIn.py ファイルに凝縮できるからです。
数学・物理・工学などにおける様々の問題の検討・考察の積み重ねでは多くのゴミ計算が発生します。そのゴミの積み重ねの結果、宝物となる式ができあがってきます。宝物の PythonSf ワンライナーができあがります。後々まで残しておきたいのは、宝物の式だけです。ゴミ計算は邪魔です。
Mathematica, Matlab などの notebook や IPython でも検討・考察の積み重ねをファイルとして残せます。でも残されている大部分の式はゴミです。宝物の式はゴミに埋もれています。昨日の notebook ならば宝物の式の位置が頭に残っていますから、有用な notebook です。でも一年前の notebook では、宝物の式とゴミとの区別が簡単にはできません。宝物の式だけの notebook を別に作れば良いのでしょうが それは面倒な作業です。
PythonSf のワンライナーならば、検討・考察の積み重ねの骨格・エッセンス・宝物だけを sfCrrntIni.py ファイルとの組合せとして自然に残せていけます。ワンライナーで完結しているので、コピー・ペーストで宝物の式だけを集めていけます。PythonSf のワンライナーが人間の考察の粒度に合っていることも、ワンライナーの積み重ねが重宝する理由です。人間が検討・思考を積み重ねていくブロックはワンライナーで記述できる程度の範囲です。大げさな言い方なのは承知していますが「PythonSf ワンライナーは数学が必要となる分野での思考・考察・検討ツールとして使える」と主張します。
以下 幾つかの宝物ワンライナーを見てやって下さい。
を主張します。petit simulation: one-liner に拘るのは、数学や物理の問題の検討に集中するためです。そのる最中にプログラミング・デバッグ作業が入ってくると、本来の目的としていることとは異なった考察に値の回転をとられてしまうからです。
# x^2+1 の根が、四元数では無限個存在することの実験的証明
seed(0); vc=normalize(randn(3)); Oc(np.r_[0,vc])
===============================
Oc(0.0, 0.85771824099774296, 0.19456459875913087, 0.47588237619125601)
seed(0); vc=normalize(randn(3)); x=Oc(np.r_[0,vc]); x^2 + 1
===============================
Oc(1.11022302463e-16)
Python での λ:labmda 式は、コンピュータ・サイエンスでの λ式 に近い仕様になっています。下の様に Church 数による自然数のモデル化ができてしまいます。
PythonSf ワンライナーたち # Church 数 2;;http://en.wikipedia.org/wiki/Church_encoding
Z='1';S =λ s:s+'1';(λ s:λ z:s(s(z)))(S)(Z)
===============================
111
# Church 数での 2 + 3
Z='1';S =λ s:s+'1';(λ s:λ z:s(s( s(s(s(z))) )))(S)(Z)
===============================
111111 Z:始めの数、任意の数に対する Successor を返す S だけから加算を実行する様子を具体的に示せています。 0→1, 1→11, 2→111, 3→1111, 4→11111, 5→111111 ... と対応させる一進方を使っています。
# 量子力学での調和振動子波動関数
P,X=:Px64,X64; H=P^2+10 X^2; vc=kzrs(64); vc[16]=1; renderMtCplx( ~[ expm(`i H t) vc for t in klsp(0, 5s`)])
# 8の字軌跡 inV=[-0.97m`,0.243m`, 0.97m`,-0.243m`, 0m`,0m`, -0.466m`/s`,-0.432m`/s`, -0.466m`/s`,-0.432m`/s`, 0.932m`/s`,0.864m`/s`]; N=len(inV)//4; getFV=λ v,i,k:(λ r=krry(v[2k:2k+2])-krry(v[2i:2i+2]):r/norm(r)^3 if norm(r)!=0 else ~[0,0])(); sumFc=λ v,j:sum([getFV(v,j,k) for k in range(N) if j!=k]); fnc= λ *v: np.r_[v[2N:],(~[sumFc(v,j) for j in range(N)]).r]; mt=kOde(fnc,inV, 2 s`,400); pt=plotTrajectory; pt(mt[:,:2]); pt(mt[:,2:4],color=red); pt(mt[:,4:6],color=green)
# 8の字軌跡で初期配置を z 軸方向に 0.1 だけずらした軌跡 D=3;inV=[-0.97m`,0.243,0, 0.97,-0.243,0, 0,0,0.1, -0.466m`/s`,-0.432,0, -0.466,-0.432,0, 0.932,0.864,0]; N=len(inV)//(2D) ; getFV=λ v,i,k:(λ r=krry(v[D k:D (k+1)])-krry(v[D i:D (i+1)]):r/norm(r)^3 if norm(r)!=0 else ~[0,0])(); sumFc=λ v,j:sum([getFV(v,j,k) for k in range(N) if j!=k]); fnc= λ *v: np.r_[v[D N:],(~[sumFc(v,j) for j in range(N)]).r]; mt=kOde(fnc,inV, 20s`,400); cl=ClCplxColor(); for k in range(N):plotTrajectory(mt[:,D k:D (k+1)],color=cl.GetFltColor(exp(`i 2pi k/N)))
# ウラムの螺旋;;http://ja.wikipedia.org/wiki/ウラムの螺旋
N=10000; ts(); lsV=[~[1,0],~[0,1],~[-1,0],~[0,-1]]; Bf(last=~[0,0], len=1, nLen=0, n4=0, first=True); f=λ k:(Bf.last, Bf(last=Bf.last+lsV[Bf.n4], nLen=Bf.nLen+1), Bf(n4=Bf.n4) if Bf.nLen<Bf.len else [Bf(n4=(Bf.n4+1)%4, nLen=0), Bf(first=False) if Bf.first == True else Bf(first=True, len=Bf.len+1)])[0]; lsPt=tn.imap(f, tn.count())[:N]; mlb(); import pylab as pb; pb.scatter( *zip( *[pos for k,pos in enumerate(lsPt) if ts.isprime(k)])); pb.show();
↑1,3,5,7,9 奇数の線が出ている? やってみる
N=10000; ts(); lsV=[~[1,0],~[0,1],~[-1,0],~[0,-1]]; Bf(last=~[0,0], len=1, nLen=0, n4=0, first=True); f=λ k:(Bf.last, Bf(last=Bf.last+lsV[Bf.n4], nLen=Bf.nLen+1), Bf(n4=Bf.n4) if Bf.nLen<Bf.len else [Bf(n4=(Bf.n4+1)%4, nLen=0), Bf(first=False) if Bf.first == True else Bf(first=True, len=Bf.len+1)])[0]; lsPt=tn.imap(f, tn.count())[:N]; plotPt([pos for k,pos in enumerate(lsPt) if k%10 in [1,3,7,9] ])
If then else 構文が入ってこない、数式を並べただけの one-liner 式ならば、プログラミング作業・デバッグ作業とは無縁です。実際、これらの PythonSf one-liner 式を作り上げていく途中では幾つもの誤りと その訂正が入っています。しかし、そのためにデバッガを立ち上げることは殆んどありません。大部分の場合、途中の数式の値を打ち出すだけでエラー原因を特定できます。PythonSf one-liner 式を書いていく作業は、手でメモ数式を書き下していく作業と殆んど同じです。
ですから、PythonSf one-liner 式での計算過程は実際に計算可能な PythonSf 式の羅列による数値実験だと言えます。だと、数学・物理・工学などの問題の考察に集中し続けられます。定理や公式に相当する関数やクラスは sfCrrntIni.py ファイルに書き込んでいきます。それらは自動的に PythonSf のグローバル名前空間に入り込んでくるので、宣言済みとして PythonSf 式中に使えます。One-liner が一行だけで独立していることが、それまでの計算過程からの文脈から独立して計算できることも、考察の積み重ねを強く支えて切れます。
PythonSf を使えば vim や emacs といったエディタを Matlab や Mathematica 以上に有用な計算ツールに変貌させられます。
PythonSf は CUI プログラムです。GUI ではありません。これは計算プログラムにとって利点となります。コンピュータでの計算作業は計算式文字列を与えて、コンピュータに計算させ、その結果を待つことの繰り返しだからです。この計算式文字列を与える作業を最も効率的に行えるのはユーザーが使い慣れたエディタです。そして CUI プログラムである PythonSf は容易にエディタに組み込めます。PythonSf と使い慣れたエディタを使って効率的に計算作業をコンピュータに行わせられます。
エディタをPython 環境としても使う
PythonSf は数式記述のためにプリプロセッサを使っていますが、その拡張文法は僅かの例外を除いて Python upper compatible です。
テスト実行 調べる
np.matrix.__mro__
===============================
(<class 'numpy.matrixlib.defmatrix.matrix'>, <type 'numpy.ndarray'>, <type 'object'>)
dir(np.ndarray)
===============================
['T', '__abs__', '__add__', '__and__', '__array__', '__array_finalize__', '__array_interface__', '__array_prepare__', '__array_priority__', '__array_struct__', '__array_wrap__', '__class__', '__contains__', '__copy__', '__deepcopy__', '__delattr__', '__delitem__', '__delslice__', '__div__', '__divmod__', '__doc__', '__eq__', '__float__', '__floordiv__', '__format__', '__ge__', '__getattribute__', '__getitem__', '__getslice__', '__gt__', '__hash__', '__hex__', '__iadd__', '__iand__', '__idiv__', '__ifloordiv__', '__ilshift__', '__imod__', '__imul__', '__index__', '__init__', '__int__', '__invert__', '__ior__', '__ipow__', '__irshift__', '__isub__', '__iter__', '__itruediv__', '__ixor__', '__le__', '__len__', '__long__', '__lshift__', '__lt__', '__mod__', '__mul__', '__ne__', '__neg__', '__new__', '__nonzero__', '__oct__', '__or__', '__pos__', '__pow__', '__radd__', '__rand__', '__rdiv__', '__rdivmod__', '__reduce__', '__reduce_ex__', '__repr__', '__rfloordiv__', '__rlshift__', '__rmod__', '__rmul__', '__ror__', '__rpow__', '__rrshift__', '__rshift__', '__rsub__', '__rtruediv__', '__rxor__', '__setattr__', '__setitem__', '__setslice__', '__setstate__', '__sizeof__', '__str__', '__sub__', '__subclasshook__', '__truediv__', '__xor__', 'all', 'any', 'argmax', 'argmin', 'argsort', 'astype', 'base', 'byteswap', 'choose', 'clip', 'compress', 'conj', 'conjugate', 'copy', 'ctypes', 'cumprod', 'cumsum', 'data', 'diagonal', 'dot', 'dtype', 'dump', 'dumps', 'fill', 'flags', 'flat', 'flatten', 'getfield', 'imag', 'item', 'itemset', 'itemsize', 'max', 'mean', 'min', 'nbytes', 'ndim', 'newbyteorder', 'nonzero', 'prod', 'ptp', 'put', 'ravel', 'real', 'repeat', 'reshape', 'resize', 'round', 'searchsorted', 'setasflat', 'setfield', 'setflags', 'shape', 'size', 'sort', 'squeeze', 'std', 'strides', 'sum', 'swapaxes', 'take', 'tofile', 'tolist', 'tostring', 'trace', 'transpose', 'var', 'view']
info(fft)
info(np.linalg.inv)
inv(a)
Compute the (multiplicative) inverse of a matrix.
Given a square matrix `a`, return the matrix `ainv` satisfying
``dot(a, ainv) = dot(ainv, a) = eye(a.shape[0])``.
Parameters
----------
a : array_like, shape (M, M)
Matrix to be inverted.
Returns
-------
ainv : ndarray or matrix, shape (M, M)
(Multiplicative) inverse of the matrix `a`.
Raises
------
LinAlgError
If `a` is singular or not square.
Examples
--------
>>> from numpy import linalg as LA
>>> a = np.array([[1., 2.], [3., 4.]])
>>> ainv = LA.inv(a)
>>> np.allclose(np.dot(a, ainv), np.eye(2))
True
>>> np.allclose(np.dot(ainv, a), np.eye(2))
True
If a is a matrix object, then the return value is a matrix as well:
>>> ainv = LA.inv(np.matrix(a))
>>> ainv
matrix([[-2. , 1. ],
[ 1.5, -0.5]])
===============================
None ##■■ Python 環境としての PythonSf
# 数値の加減乗除べき乗算
(1-2*3/4)^5
===============================
-0.03125
# sin(1/x) value at x=pi
sin(1/`X)(pi)
===============================
0.312961796208
# 数値微分値: sin(1/x) value at x=pi
∂x( sin(2/`X) )(`π)
===============================
-0.162946719226
# シンボリック微分: sin(1/x)
ts(); ∂x( ts.sin(1/`x) )
===============================
-cos(1/x)/x**2
# Groebner 基底をシンボリックに計算する
ts();x,y,z=ts.symbols('x y z');f1,f2,f3=[x+y^2+3z^2-4, 4y^2-5,y^4-5z-10]; ts.groebner([f1,f2,f3], [x,y,z])
===============================
[-5/4 + y**2, 1483/256 + x, 27/16 + z]
# 行列とベクトルの積演算
# |1,2| * |5|
# |3,4| |6]
mt,vc=~[[1,2],[3,4]], ~[5,6]; mt vc
===============================
[ 17. 39.]
---- ClTensor ----
# W:ワット、A:アンペア単位付きの数値計算
ts(); wattage,current=100W`,2.3A`; wattage/current^2
===============================
18.9035916824197*V`/A`
# Bool 体係数多項式の商と剰余
(`P^7+1)/(`P^2+1)
===============================
(Pl(`P^5+`P^3+`P), Pl(`P+1))
x=`P; (x^7+1)%(x^2+1)
===============================
`P+1
# 楕円関数:第一種の不完全/Jacobi 楕円関数の計算
φ,m=pi/3,0.6; sy(); u=ss.ellipkinc(φ,m); ss.ellipj(u,m)
===============================
(0.8660254037844386, 0.50000000000000011, 0.74161984870956643, 1.0471975511965976)
# Sn(4) 置換群における 置換集合:{Sb(2,3,0,1), Sb(1,0,3,2),Sb(1,3,2,0)} の左剰余類
=:SS4; SS4/{Sb(2,3,0,1), Sb(1,0,3,2),Sb(1,3,2,0)}
===============================
kfs([Sb(0,1,2,3), Sb(0,1,3,2), Sb(0,2,1,3), Sb(0,2,3,1), Sb(0,3,1,2), Sb(0,3,2,1)])
# 数値 1234 と文字列 '1' の hash コードを確認する Python テスト・コード
hash(1234), hash('1')
===============================
(1234, 1977051568)
# グラフ描画: sin(1/x) を [0.2, pi] 領域で
plotGr( sin(1/`X), 0.2, pi )
[1](#test name reference)
PythonSf ワンライナー;;http://localhost:4000/pysf/manual/one-liners.htm#kOde:%E5%B8%B8%E5%BE%AE%E5%88%86%E6%96%B9%E7%A8%8B%E5%BC%8F
D=2;inV=[-0.97m,0.243, 0.97,-0.243, 0,0, -0.466m/s,-0.432, -0.466,-0.432, 0.932,0.864]; N=len(inV)//(2D) ; getFV=λ v,i,k:(λ r=krry(v[D k:D (k+1)])-krry(v[D i:D (i+1)]):r/norm(r)^3 if norm(r)!=0 else ~[0,0])(); sumFc=λ v,j:sum([getFV(v,j,k) for k in range(N) if j!=k]); fnc= λ *v: np.r_[v[D N:],(~[sumFc(v,j) for j in range(N)]).r]; mt=kOde(fnc,inV, 2 s,400); cl=ClCplxColor(); for k in range(N):plotTrajectory(mt[:,D k:D (k+1)],color=cl.GetFltColor(exp(`i 2pi k/N)))
pysf.vim スクリプト関数・機能表
| 関数名 | 機能 |
|---|---|
| ExecPySf_1liner() | PythonSf ワンライナー式の実行 |
| ExecPySfOp_1liner() | PythonSf Open ワンライナー式の実行 |
| ExecPySf_start_1liner() | PythonSf ワンライナー式のスタート実行 |
| ExecSf_Block() | PythonSf コード・ブロックの実行 |
| ExecSfOp_Block() | PythonSf Open コード・ブロックの実行 |
| Exec_command() | OS コマンドの実行 |
| Exec_start() | OS コマンドの start 実行 |
| ExecPy_Block() | Python コード・ブロックの実行 |
| Exec_BlockCntn() | 任意コード・ブロックの生成と連続実行 |
| ConvertAlpbt2Greek() | ASCII ギリシャ文字漢字変換 |
| GetDateTime() | 現在年月日時刻文字列の取得 |
| StartGoogleSearchUnderCursor() | Google 検索開始 |
##■■ Vim での pysf.vim script 組み込み Vim エディタで PythonSf 計算をさせるには pysf.vim script を Vim に組み込みます。その手順は簡単です。Git で配布している pysf.vim を Vim がインストールされているディレクトリの ..\vim73\plugin\に置くだけです。キー・バインドは pysf.vim にハード・コーディングされています。
##■■ Vim での計算例 Vim エディタで PythonSf 計算をさせるには pysf.vim script を使います。このスクリプトを組み込んだ Vim も Git での PythonSfCp932 の配布ファイルに入っています。Windows で Vim を使える方は、評価のためには こちらを使われると便利です。ダウンロードした git working directory で下のコマンドを実行させるだけで Python Sf 計算を始められます。
vim\gvim.exe
\(\pi^{0.5}\) を計算したいときの Vim エディタ操作例を見てみましょう。 Vim エディタで計算をするときは、 pi^0.5 式の文字列行を打ち込み、その行にカーソルを置いたまま Vim normal mode で ;j 操作を行います。
pi^0.5
すると Vim 画面最下段のコマンド・エリアに下のように計算結果が表示されます
===============================
1.77245385091
この計算結果文字列は Vim の「特殊レジスタ 0 と *」にも残されています。エディット・テキストにも計算結果を残したいときは、Vim の paste コマンド p を実行します。するとエディット画面は下のようになり、後で計算式と計算結果を参照できるようになります。
pi^0.5
===============================
1.77245385091
「Matlab や Mathematica を超える」などと不遜なことをいうのですから、電卓計算以上のことも もちろん可能です。例えば \(\int_{-\infty}^{+\infty} e^{-x^{2}} dx\) 定積分値は下の PythonSf 式で計算できます。
quadR(exp(-`X^2), -np.inf, np.inf)
===============================
1.77245385091
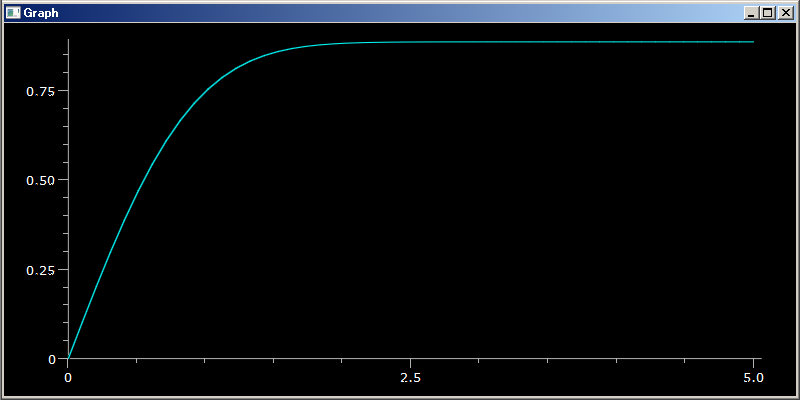
[0,t] 領域の積分値として定まるエラー関数 \(\int_{0}^{t} e^{-x^{2}} dx\) のグラフを下の PythonSf 式で描かせられます。
plotGr(λ t:quadR(exp(-`X^2), 0, t), 0,5)
##■■ C++/Boost プログラムのコンパイルと実行 pysf.vim マクロは PythonSf の計算以外でも活用できます。”;e” で //@@ … //@@@ ブロックのファイル化に続けてコマンドを連続実行します。 “;a” 操作でカーソル下の一行を OS コマンドとみなして実行します。 この二つの操作を活用することで、Vim エディタ上で任意のプログラムのテスト・コンパイルと実行が可能です。
何時でも再実行可能な形でノートに残せます。どのようにリンクして、どんな引数で実行するかまで残っています。
一行で完結している。それ以前の文脈の影響を受けない import 済みのモジュールはディレクトリごとに sfCrrntIni.py で固定される ↑ if then else 構文の排除
kOde ← scipy.integrate.ode を one-liner で扱いやすいように修正したもの ↑ ode(..) は時刻引数を明示的に扱わねばならないなど、ワンライナーでは扱いにくい。
D=2;inV=[-0.97m,0.243, 0.97,-0.243, 0,0, 1,1, -0.466m/s,-0.432, -0.466,-0.432, 0.932,0.864, 0,0]; N=len(inV)//(2D) ; getFV=λ v,i,k:(λ r=krry(v[D k:D (k+1)])-krry(v[D i:D (i+1)]):r/norm(r)^3 if norm(r)!=0 else ~[0,0])(); sumFc=λ v,j:sum([getFV(v,j,k) for k in range(N) if j!=k]); fnc= λ *v: np.r_[v[D N:],(~[sumFc(v,j) for j in range(N)]).r]; mt=kOde(fnc,inV, 2 s,400); cl=ClCplxColor(); for k in range(N):plotTrajectory(mt[:,D k:D (k+1)],color=cl.GetFltColor(exp(`i 2pi k/N)))
↑ if then else 構文が不必要
type _tmC.py
キーボードからマウスに手を移し変える、うざったい操作は一切ありません。
Eclips や VisualStudio といった統合環境では、小さなテスト・プログラムを大量に
###
git push のような時間のかかる操作には ;a 操作を使うべきではありません。途中経過を表示できないからです。
blog comments powered by Disqus